4.3. Обслуживание вызовов примитивного потока

Определение вероятностей состояния полнодоступного пучка.

Полнодоступный пучок емкостью (1<) линий, включенных в выходы неблокирующей коммутационной системы с потерями, обслуживает вызовы, которые образуют примитивный поток с параметром _i. Длительность обслуживания вызова коммутационной системой распределена по показательному закону F(t)=1–е^-t, =1. Требуется определить вероятности различных состояний полнодоступного пучка в процессе обслуживания поступающих вызовов и вероятности потерь по времени p_t, вызовам р_в и нагрузке р_н.

Примитивный поток является частным случаем симметричного потока с простым последействием. Его параметр _i определяется соотношением

где  – параметр потока вызовов свободного источника; п – число источников вызовов, каждый из которых создает поток с одним и тем же значением параметра . Из (4.37) следует, что параметр примитивного потока _i пропорционален числу свободных источников, он зависит лишь от числа занятых линий пучка i.

Подставляя в (4.13) соотношение _k=(n–k), получим

Последняя формула называется формулой Энгсета. Она определяет вероятность р_i того, что в полнодоступном пучке емкостью  линий, который включен в неблокирующую коммутационную систему с потерями и обслуживает вызовы примитивного потока, в любой произвольный момент времени занято точно i линий, или, иными словами, вероятность того, что этот пучок находится в состоянии i.

В гл. 2 было показано, что простейший поток можно рассматривать как предельный частный случай примитивного потока. Естественно, что формула Энгсета (4.38) является более общей, чем формула Эрланга (4.16), и последняя может быть непосредственно получена из (4.38). Покажем это.

Число источников вызовов устремим к бесконечности (n), одновременно устремив к нулю параметр одного свободного источника (). При этом параметр потока вызовов всех свободных источников па сохраняем величиной конечной и постоянной – =n=const. Тогда при любом конечном значении i (i=0, 1,..., ...,)

Таким образом, при п из формулы Энгсета получается формула Эрланга.

Соотношения между параметром потока а и нагрузкой, поступающей от одного источника. Рассмотрим систему без потерь, т. е. систему, в которой число линий равно числу источников (=п). В такой системе каждый источник может обслуживаться независимо от состояния других источников. Поэтому достаточно рассмотреть случай n==1. При этом по (4.38) получаем: p₀=l/(l+); p₁=/(l+). Вероятность p₁ в рассматриваемом случае есть доля времени, в течение которого источник занят в системе без потерь, что численно соответствует интенсивности нагрузки а, поступающей от одного источника – р₁=а. Отсюда

Установим соотношение между параметром потока вызовов, поступающих от одного источника в системе без потерь, и параметром потока а одного свободного источника. Согласно определению параметр потока есть Вероятность ₁(t, t+) того, что за промежуток времени [t, t+), 0, от рассматриваемого источника поступит один и более вызовов, определяется произведением вероятности р₀ того, что в момент t источник свободен, на сумму, состоящую из вероятности того, что за промежуток времени [t, t+t) от свободного источника поступит точно один вызов (эта вероятность равна +о()), и вероятности поступления за этот промежуток более одного вызова (вероятность равна о()). Поэтому ₁(t, t+)=р₀(+о()), и параметр потока вызовов одного источника равен

Таким образом, параметр потока вызовов одного источника численно равен интенсивности поступающей нагрузки от одного источника.

Заменим в (4.38) параметр а соотношением (4.39) и получим формулу Энгсета, выраженную через величину интенсивности поступающей от одного источника нагрузки а:

т. е. вероятность того, что в произвольный момент времени из п источников занято точно i источников, определяется распределением Бернулли.

Определение вероятностей потерь по времени, вызовам и нагрузке. Потери по времени p_t численно равны вероятности занятости всех  линий пучка:

Формулу для вычисления потерь по вызовам получим из соотношения (4.15), подставив в него значения параметра примитивного потока вызовов:

Соотношения (4.38), (4.41) и (4.44) показывают, что вероятности p_i состояний полнодоступного пучка линий в процессе обслуживания примитивного потока вызовов, а также потери p_t, р_в зависят от числа источников вызовов п, величины поступающей от одного источника нагрузки а (или параметра потока вызовов одного свободного источника ) и емкости пучка линий .

Из сопоставления (4.44) и (4.43) следует, что в полнодоступном пучке емкостью  линий, на который поступает примитивный поток вызовов, потери по вызовам при наличии п источников равны потерям по времени при наличии п–1 источников, т. е. р_в(n, а, )=p_t(n–1, a, ). Отсюда следует, что р_в(п, a, )<p_t(n, a, ), или р_в<р(t)

Формула (4.44), определяющая потери по вызовам р_в(п, a, ), табулирована для широкого диапазона значений п, a, . По этим же таблицам определяют потери по времени, исходя из равенства p_t(n, а, )=р_в(n+1, a, ).

Согласно определению, вероятность потерь по нагрузке р_н равна отношению интенсивности потерянной y_п к интенсивности поступающей у нагрузок: р_н=у_п/y.

Интенсивность потерянной нагрузки у_п есть разность интенсивностей поступающей у и обслуженной у₀ нагрузок: y_п=y–y₀. Интенсивность обслуженной нагрузки у₀ равна математическому ожиданию числа одновременно занятых линий пучка емкостью :

Аналогично интенсивность поступающей нагрузки у равна математическому ожиданию числа занятых линий в пучке емкостью n (в системе без потерь):

Таким образом, интенсивность поступающей нагрузки равна произведению числа источников п, создающих эту нагрузку, на интенсивность нагрузки а одного источника. Из соотношения (4.46) также следует, что математическое ожидание числа занятых линий M(i) в системе без потерь составляет M(i)=na.

Используя соотношение (4.45) и (4.46), находим

Упростим числитель последней дроби; развернем значения приведенных в числителе рядов и сгруппируем все коэффициенты, относящиеся к параметру , имеющему одну и ту же степень. В

С учетом (4.43) получаем формулу, определяющую потери по нагрузке:

Из этой формулы следует, что потери по нагрузке р_н меньше потерь по времени p_t(р_н<р_t) и даже в предельном случае, когда =п, потери по нагрузке р_н = 0, а потери по времени (4.43) p_t=а_п. Можно показать, что потери по нагрузке р_н всегда меньше и потерь по вызовам р_в.

Таким образом, при обслуживании примитивного потока вызовов полнодоступным пучком, включенным в неблокирующую коммутационную систему, потери по нагрузке меньше потерь по вызовам, а последние меньше потерь по времени, т. е. имеет место неравенство

При обслуживании же таким пучком простейшего потока вызовов, как было показано (4.28), между этими потерями имеет место равенство

Сравнение пропускной способности полнодоступного пучка, обслуживающего вызовы примитивного и простейшего потоков. Характер зависимости величины поступающей нагрузки па от емкости пучка линий , который обслуживает вызовы примитивного потока, поступающие от фиксированного числа источников п, такой же, как и при обслуживании вызовов простейшего потока. Однако н а пропускную способность пучка влияет число источников вызовов п: в области малых потерь с уменьшением п увеличивается пропускная способность пучка. Это иллюстрируется семейством кривых na=f() при р_в=0,005, приведенном на рис. 4.9. Эти кривые одновременно показывают, что при заданном качестве обслуживания поступающая на  линий пучка нагрузка па, создаваемая вызовами примитивного потока от любого числа источников, имеет большую величину по сравнению с нагрузкой у, создаваемой вызовами простейшего потока. Так, при =30 нагрузки, поступающие от n₁=50 и n₂=100, могут достигать соответственно значений na₁=21,65 Эрл и nа₂ = 20 Эрл, а нагрузка, которая создается вызовами простейшего потока, y=18,7 Эрл, т. е. нагрузка от n=50 на 8,2% больше нагрузки, поступающей от n=100, и на 16% больше нагрузки, создаваемой вызовами простейшего потока. Заметим, что с увеличением потерь р_в: а) существенно уменьшается влияние п на пропускную способность пучка; б) сокращается различие между пропускной способностью пучков, обслуживающих вызовы примитивного и простейшего потоков. В то же время нагрузка па_o, обслуживаемая полнодоступным пучком  в области любых потерь, выше при обслуживании вызовов примитивного потока (па_o=па(1–р_н)), а р_н всегда меньше E_(na). Так, например, обслуженная нагрузка, создаваемая примитивным потоком от n=50, при р_н=E_(nа)=0,01 на 12% и при p_н=E_(na)=0,2 на 6% выше обслуженной нагрузки, создаваемой простейшим потоком вызовов. Таким образом, с точки зрения величины обслуживаемой нагрузки примитивный поток всегда «лучше» простейшего потока вызовов.

Обслуживание вызовов, поступающих от источников с различной интенсивностью. В модели примитивного потока принято, что параметр потока вызовов от любого свободного источника один и тот же – . Поэтому параметр потока вызовов _i от группы из п источников в каждый момент времени зависит только от числа свободных в этой группе источников – _i=(п–i), где i – число занятых источников. Вероятность потери вызова для каждого источника одна и та же. В реальных условиях свободные источники имеют различные параметры потоков – ₁₂...._n. В связи с этим параметр потока вызовов от группы источников в каждый момент времени зависит не только от числа свободных в группе источников, но и от того, какие именно источники в данный момент свободны. Каждое состояние такой системы с (п–i) свободными источниками характеризуется строго определенным набором i занятых источников. Вероятность потери вызова для каждого источника имеет различное значение.

Если качество обслуживания вызовов примитивного потока характеризуется одним параметром – вероятностью потерь по вызовам р_в, определяемой для полнодоступного пучка формулой Энгсета (4.44), то качество обслуживания вызовов при неодинаковой интенсивности источников характеризуется двумя величинами – вероятностью _o потери вызова потока, общего для всей группы источников, и вероятностями _j(j=1, 2,..., п) потери вызова каждого из n источников. Исследованиями установлено следующее.

1. Полнодоступный пучок емкостью  линий всегда обладает более высокой пропускной способностью при обслуживании вызовов, создаваемых группой в n источников с ₁₂..._n, по сравнению с обслуживанием этим пучком вызовов примитивного потока также от группы в n источников. Иными словами, при условии при одной и той же емкости пучка  вероятность _o всегда меньше р_в.

2. Значения вероятностей потери вызова _j(j=1,...,n) находятся в широком диапазоне: у источников с большей интенсивностью значение _j меньше, чем у источников с меньшей интенсивностью; у ряда источников _j может превышать вероятность _o и даже вероятность р_в.

Задача 4.1.

Полнодоступные пучки емкостью ₁=20, ₂=40 и ₃=60 линий обслуживают простейшие потоки вызовов. На пучок ₁ в утренний и вечерний ЧНН поступают нагрузки интенсивностью y_1y=12,4 Эрл, y_1в=11,1 Эрл, на пучок ₂–y_2y=30,0 Эрл, y_2в=27,5 Эрл, на пучок ₃– у_3y=49,0 Эрл, y_3в=45,0 Эрл.

Определить: а) потери p_i, р_в и р_н в пучках ₁, ₂ и ₃; б) соотношения между относительными величинами изменения потерь и поступающей нагрузки в каждом из этих пучков.

Решение, а) Согласно (4.28) p_t=р_в=p_н=E_(y). По таблицам первой формулы Эрланга находим:

E_1(y_1в)=E₂₀(11,1)=0,0050; E_1(у_1y)=E₂₀(12,4)=0,0127;

E_2(y_2в)=E₄₀(27,5)=0,0053; E_2(y_2у)=E₄₀(27,5)=0,0144;

E_3(y_3в) =E₆₀(45,0)=0,0054; Е_3(y_3у)=E₆₀(49,0)=0,0172.

б) Относительные величины изменения потерь _п и изменения нагрузки _н определяются из соотношений

Аналогично определяем: при ₂=40 _п2=172%, _н2=9,1% и при ₃=60 _п3=219%, _н3= 8,9%.

Соотношения между _п и _н для пучков ₁, ₂ и ₃ соответственно составляют: _п1/_н1=13,2; _п2/_н2=18,9; _п3/_н3=24,6.

Следует подчеркнуть, что при рассмотренных в этой задаче значениях потерь, которые соответствуют реальным потерям на городских телефонных сетях, увеличение поступающей нагрузки примерно на 10% приводит к увеличению потерь в 2,5–3 раза, т. е. потери возрастают в 10–25 раз быстрее по сравнению с величиной интенсивности поступающей нагрузки.

Задача 4.2.

От трех групп источников поступают вызовы, образующие простейшие потоки и создающие нагрузки, интенсивности которых составляют y₁=10, y₂=20 и y₃=40 Эрл. Эти вызовы обслуживаются полнодоступными пучками.

Определить: а) требуемые емкости пучков, если потери не должны превышать E_(у)₁0,005 и E_(y)₂0,02; б) соотношения между относительными величинами приращения емкости пучков линий и увеличения интенсивности поступающей нагрузки при заданном качестве обслуживания.

Решение: а) По таблицам формулы Эрланга при заданных величинах интенсивности поступающей нагрузки у и заданных значениях потерь Е_(у) определяются требуемые емкости пучков линий:

Допустимая величина потерь	Емкость пучков линий, при интенсивности поступающей, нагрузки, Эрл
	y1=10	y2=20	y3=40
Е(у)1	1=19	2=31	3=55
E(y)20,02	1=17	2=28	3=50

б) Относительные величины приращения емкости пучков линий _ и увеличения интенсивности поступающей нагрузки _н определяются из соотношений:

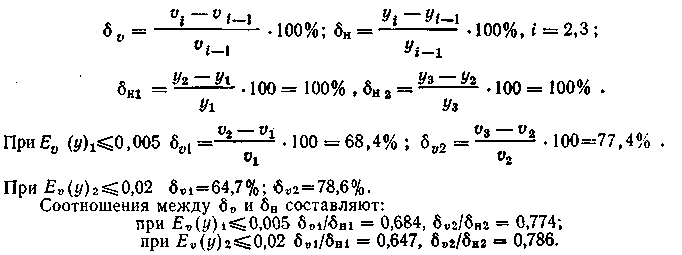
Решение этой задачи показывает, что: а) если на полнодоступный пучок поступают нагрузки интенсивностью y=1040 Эрл, то в области малых потерь увеличение потерь с E_(y)₁0,005 до E_(y)₂ (в 4 раза) позволяет уменьшить требуемые емкости пучков линий только примерно на 10%; б) в области малых потерь (реальных потерь, имеющих место на ГТС) и относительно небольших значений интенсивности поступающей нагрузки (у=1040 Эрл) емкости требуемых пучков возрастают медленнее по сравнению с величиной поступающей нагрузки. При фиксированной величине потерь увеличение интенсивности поступающей нагрузки в 2 раза приводит к увеличению емкости пучка только на 65–80 %.

Задача 4.3.

Определить: требуемые емкости  полнодоступного пучка при обслуживании поступающей нагрузки интенсивностью па=10 Эрл, создаваемой вызовами примитивного потока от п=100, 50 и 25 источников; допустимые потери р_в0,005. Сопоставить найденные емкости пучков  с емкостью ₀ полнодоступного пучка, обслуживающего ту же нагрузку, создаваемую вызовами простейшего потока.

Решение. Определяем значения нагрузки а, поступающей от одного источника, для групп источников емкостью п=100, 50 и 25 и по таблицам формулы Энгсета отыскиваем при р_в0,005 соответственно требуемые емкости пучков ₁, ₂, ₃: a₁=0,1 Эрл; а₂=0,2 Эрл; а₃=0,4 Эрл; ₁=18; ₂=18; ₃=16.

По таблицам формулы Эрланга отыскиваем емкость пучка ₀ при y=10 Эрл и потерях E_0(10)0,005–₀=19.

Таким образом, по сравнению с обслуживанием простейшего потока вызовов обслуживание примитивного потока, создаваемого п=100 и 50 источниками вызовов, при высоком качестве обслуживания (р0,005) позволяет сократить емкость полнодоступного пучка только на одну линию (на 5%), а при n=25–на три линии (на 16%).

Задача 4.4.

Полнодоступный пучок емкостью = 8 линий обслуживает вызовы примитивного потока от n=30 источников с а=0,1; 0,3; 0,5 Эрл.

Определить: а) величины обслуженных нагрузок ап_o; б) соотношения между потерями по вызовам и обслуженными нагрузками и сопоставить полученные результаты с аналогичными характеристиками полнодоступного пучка той же емкости при обслуживании им вызовов простейшего потока, создающими нагрузку у = па.

Решение. По таблицам Энгсета отыскиваем значения потерь по вызовам p_в=р(п, а, ) и потерь по времени р_t=р(n+1, a, ) для заданных значений

р_в=р(30; 0,1; 8)=0,0047; р_t=р(31; 0,1; 8)=0,0058;

p_в=р(30; 0,3; 8)=0,3286; р_t=р(31; 0,3; 8)=0,3479;

p_в=р(30; 0,5; 8)=0,6629; р_t=р(31; 0,5; 8)=0,6761.

Рассчитываем по (4.47) потери по нагрузке р_н и величины обслуженных нагрузок па_o=па(1–р_н) при:

а=0,1 Эрл – р_н=0,0043; nа_o=2,9871 Эрл;

а=0,3 Эрл – р_н=0,2551; па_o=6,7041 Эрл;

а=0,5 Эрл–р_н=0,4958; nа_o=7,5630 Эрл.

Затем определяем значения нагрузок у, создаваемых вызовами простейшего потока, и по таблицам первой формулы Эрланга отыскиваем значения потерь E_(y) и обслуженных нагрузок у_о=у(1–E_(y)):

а=0,1 Эрл – у=3 Эрл; E₈(3)=0,0081; y_o=2,9757 Эрл;

а=0,3 Эрл – у=9 Эрл; E₈(9)=0,2892; y_o=6,3972 Эрл;

а=0,5 Эрл – y=15 Эрл; E₈(15)=0,5193; y_o=7,2105 Эрл.

Наконец, определяем требуемые соотношения при:

а=0,1 Эрл – p_в/na_o=0,0016; Е₈(3)/у_o=0,0027;

а=0,3 Эрл – р_в/na_о=0,049; Е₈(9)/у_o=0,045;

а=0,5 Эрл – р_в/nа_o = 0,088; E₈(15)/y_о=0,072.

Эта задача иллюстрирует следующие закономерности: 1) при любых потерях по вызовам обслуживаемая полнодоступным пучком нагрузка выше, если на пучок поступают вызовы примитивного потока; 2) при малых потерях вызовы примитивного потока обслуживаются с более высоким качеством по сравнению с вызовами простейшего потока (p_в/na_o<E_(y)/y_o), а при больших потерях, наоборот, вызовы примитивного потока обслуживаются хуже вызовов простейшего потока (p_в/na_o>E_(y)/y_o).