
- •Вопрос №1. Декартова прямоугольная и полярная с-ма коорд.
- •Гипербола.
- •Вопрос №9.Системы линейных уравнений.
- •3 Вектора , и наз компланарными, если они лежат в одной плоскости. Сумма 2х векторов и -вектор , начало кот совпадает с началом вектора , а конец – с концом .
- •Предел ф-и.
- •Бесконечно большие и бесконечно малые ф-и.
- •Вопрос №20.Производная и дифференциал ф-ции. Правило дифференцирования.
- •Теорема Лагранжа.
- •Признак и .
- •Асимптоты.
- •Неопределенный интеграл и его св-ва.
- •Предел.
- •Частные производные 1-го порядка
- •Экстремум ф-и двух переменных.
- •Вопрос №33.Понятие двойного и тройного интеграла.
- •Однородные ду
Вопрос №1. Декартова прямоугольная и полярная с-ма коорд.
Прямоуг с-ма коорд на пл.
Две
взаимноперпендикулярные оси Ох и Оу,
имеющие общее начало О и одинаковую
масштабную ед образ прямоуг.
с-му
коорд на пл. Ось Ох-ось абсцисс, ось
Оу-ось ординат, точка О-начало координат.
Плоскости, расположенные на осях Ох и
Оу назыв. корд. плоскостями и обозн ось
ХУ. Пусть М-произв т, опустим перпендик
на ось Ох и Оу соотв. МА и МВ. Точке М на
пл ставят в соотв-е 2 числа: абсциссу
![]() и ординату
и ординату
![]() .
=расстоянию
от О до А взятому со знаком «+» если А
лежит правее О и «-« - если левее.
=расстоянию
от О до В, взятому со знаком «+» если В
выше О и «-« - если ниже. (рис.)
.
=расстоянию
от О до А взятому со знаком «+» если А
лежит правее О и «-« - если левее.
=расстоянию
от О до В, взятому со знаком «+» если В
выше О и «-« - если ниже. (рис.)
Абсцисса и ордината в точке М, наз прямоугд декартовыми коорд т М. Введение прямоуг. с-мы координат позволяет установить взаимнооднозначное соотв-е между всеми точками пл и множ-вом пар чисел, что дает при решении геом. задач применять алгебраич м-ды.
Полярная с-ма координат(П.С.К.).
П
Е
М
О (рис.)
Пусть задана полярная с-ма координат и
пусть М-произв. точка пл. Положим –это
расст ОМ, -угол,
на к-рый нужно повернуть полярную ось
для совмещ с лучом ОМ. Полярными
координатами точки М наз-ют числа
и ,
при этом -1-ая
координата, -2-ая,
называемая полярным углом. Точка М обозн
(рис.)
Пусть задана полярная с-ма координат и
пусть М-произв. точка пл. Положим –это
расст ОМ, -угол,
на к-рый нужно повернуть полярную ось
для совмещ с лучом ОМ. Полярными
координатами точки М наз-ют числа
и ,
при этом -1-ая
координата, -2-ая,
называемая полярным углом. Точка М обозн
![]() ,
при чем (0,+),
.-рав-во
1.
Однако в ряде случаев прих рассматривать
углы больше ,
а также отриц. углы, т.е. отсчитываемые
от полярной оси по часовой стрелке.
Полюсу О соотв-ет полярный радиус =0,
а полярный угол не определен.
,
при чем (0,+),
.-рав-во
1.
Однако в ряде случаев прих рассматривать
углы больше ,
а также отриц. углы, т.е. отсчитываемые
от полярной оси по часовой стрелке.
Полюсу О соотв-ет полярный радиус =0,
а полярный угол не определен.
Связь между полярными и Декартовыми координатами.
Б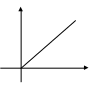 удем
предполагать, что начало прямоуг. с-мы
координат нах в полюсе О, а полож. полуось
абсцисс совпадает с направлением
полярной оси. Пусть М имеет прямоуг.
корд.
удем
предполагать, что начало прямоуг. с-мы
координат нах в полюсе О, а полож. полуось
абсцисс совпадает с направлением
полярной оси. Пусть М имеет прямоуг.
корд.
![]() и
полярные
и
полярные![]() .
(рис.) Не сложно показать, что
.
(рис.) Не сложно показать, что
![]() (1). Ф-лы (1) выражают прямоуг. корд. через
полярные. Выразим полярные коорд. через
прямоуг.
(1). Ф-лы (1) выражают прямоуг. корд. через
полярные. Выразим полярные коорд. через
прямоуг.
![]()
![]() (2).
Разделим второе ур-ние на первое
(2).
Разделим второе ур-ние на первое
![]() (3). Заметим, что ф-ла (3) определяет 2
значения полярного угла .
Из этих двух значений выбираем то, при
к-ром вып-тся рав-во 1.
(3). Заметим, что ф-ла (3) определяет 2
значения полярного угла .
Из этих двух значений выбираем то, при
к-ром вып-тся рав-во 1.
Вопрос №2.Простейшие задачи аналитической геометрии.
Расстояние между двумя точками.
Пусть
задана прямоуг. с-ма коорд. Для любых 2х
точек
![]() и
и
![]() на пл расст
на пл расст
![]() выраж ф-лой:
выраж ф-лой:
![]()
Деление отрезков в данном отношении.
Дано:
произв отрезок М1М2
и пусть М-произв. т этого отрезка, отличная
от М2.
Число
![]() - отношение, в к-ром М делит отрезок М1М2.
Если
- отношение, в к-ром М делит отрезок М1М2.
Если
![]() делит отрезок М1М2
в отнош. ,
то корд. этой точки определяются рав-вом
делит отрезок М1М2
в отнош. ,
то корд. этой точки определяются рав-вом
![]() ,
где
,
где
![]() -коорд.
М1,
-коорд.
М1,
![]() -М2.
-М2.
Площадь треугольника.
Т.
Для любых точек
![]() не лежащих на одной прямой,
не лежащих на одной прямой,
![]() выражается
ф-лой
выражается
ф-лой
![]()
Вопрос №4.Угол между прямыми на плоскости.
Рассм
2 прямые
![]() ,
,
![]() и
и
![]()
У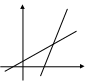 глом
между прямыми
и
глом
между прямыми
и
![]() наз меньший из смежных углов, образованных
этими пересекающимися прямыми. Очевидно,
что .
Не сложно заметить, что
наз меньший из смежных углов, образованных
этими пересекающимися прямыми. Очевидно,
что .
Не сложно заметить, что
![]() .
Тогда
.
Тогда
![]()
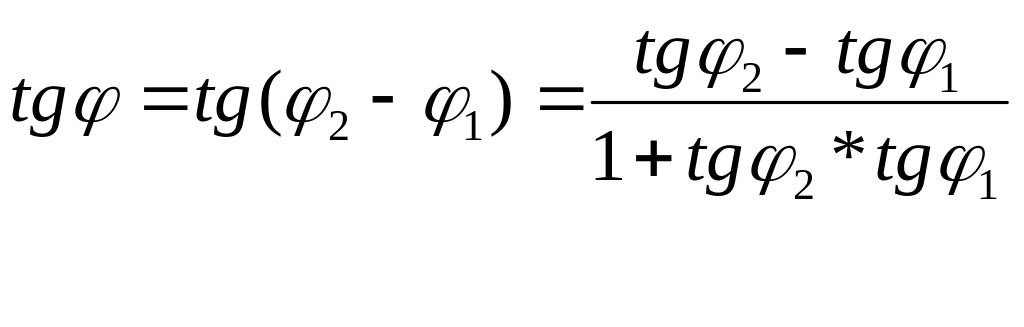 ,
то
,
то
![]() -это
-это
![]() ,
,
![]() -это
-это
![]()
![]() .
Если прямые параллельны, тогда =0,
.
Если прямые параллельны, тогда =0,
![]() .
След-но
=
-
условие
параллельности прямых.
Если прямые ,
то
.
След-но
=
-
условие
параллельности прямых.
Если прямые ,
то
![]() ,
,
![]() ,
след-но
,
след-но
![]() ,
т.е.
,
т.е.
![]() - условие
перпендикулярности прямых.
- условие
перпендикулярности прямых.
Вопрос №3.Ур-ние прямой на плоскости
Пусть
на пл задана прямоуг. с-ма координат и
нек-рая линия![]() .Ур
вида
.Ур
вида
![]() связывающее переменные
связывающее переменные
![]() и
и
![]() наз ур
линии
(в заданной с-ме координат); если этому
ур-нию удовлетвор коорд любой точки,
лежащей на линии
и не удовлетворяют координаты никакой
др точки, не лежащей на линии
.
наз ур
линии
(в заданной с-ме координат); если этому
ур-нию удовлетвор коорд любой точки,
лежащей на линии
и не удовлетворяют координаты никакой
др точки, не лежащей на линии
.
Ур-ние прямой с угловым коэффициентом.
Пусть
![]() прямая,
не параллельная оси Оу.
прямая,
не параллельная оси Оу.
Обозначим
точки пересечения
![]() с Оу точкой В, а угол между полож.
направлением оси Ох и
обозначим
.
наз углом наклона
к Ох (и в пределах от
). Пусть М(х,у)- произвольная точка прямой.
с Оу точкой В, а угол между полож.
направлением оси Ох и
обозначим
.
наз углом наклона
к Ох (и в пределах от
). Пусть М(х,у)- произвольная точка прямой.
![]() Величину
Величину
![]() обозначают
обозначают
![]() и наз угловым коэффициентом прямой.
Тогда ур примет вид
и наз угловым коэффициентом прямой.
Тогда ур примет вид
![]() –ур-е
прямой с угловым коэфф, в частности если
=0,
то =0,
прямая параллельна оси Ох. с ур-нием
–ур-е
прямой с угловым коэфф, в частности если
=0,
то =0,
прямая параллельна оси Ох. с ур-нием
![]() если
=0
и
если
=0
и
![]() получаем ур-ние оси Ох.
получаем ур-ние оси Ох.
Уравнение прямой по точке и .
Пусть
данная прямая имеет угловой коэф.
и проходит через точку
.
Искомое ур-ние прямой
.
Подставим коорд. точки М1в
ур-ние
![]()
![]()
Ур-ние прямой, проходящей через 2 данные точки.
Пусть
искомая прямая прох через точки
и
.
Искомое ур
,
где
и
![]() неизвестны. Т.к. прямая прох через М1,
то
,
т.к. прямая прох через М2,
то
неизвестны. Т.к. прямая прох через М1,
то
,
т.к. прямая прох через М2,
то
![]() .
Выразим из первого ур-ния
и подставим во второе
.
Выразим из первого ур-ния
и подставим во второе
![]()
![]()
Общее ур-ние прямой.
Т.
Каждая прямая на плоскости с прямоуг.
с-мой корд. определяется ур-нием первой
степени
![]() ,
где
,
где
![]() и
одновременно не равны 0.
и
одновременно не равны 0.
![]() определяет
нек-рую прямую на плоскости.
определяет
нек-рую прямую на плоскости.
Это ур-ние называют общим ур-нием прямой на плоскости.
Ур-ние прямой, отрезка на осях координат.
Пусть
прямая пересекает Ох и Оу соотв-но в
точках А и В. Применяем ф-лу ур-ния прямой
по двум точкам. Координаты А(а;0) и В(0;в):
![]()
Получаем
ур-ние
![]() -
ур-ние прямой на отрезках координат.
-
ур-ние прямой на отрезках координат.
Вопрос №5. Расст от т до прямой на пл и взаим распол прямых на пл.
Расстояние от точки до прямой на плоскости.
Т.
Расст.
от данной точки
![]() до данной прямой
,
заданной ур
на
пл задается ф-лой
до данной прямой
,
заданной ур
на
пл задается ф-лой
![]()
2)Взаимное расположение двух прямых на плоскости.
Пусть
прямые
и
заданы своими общими ур-ми
![]()
Рассм. с-му, состоящих из этих ур-ний с неизвестными и .
![]()
![]()
1
случай:
![]() ,
,
![]() ур-ние имеет бескон множ-во решений.
(прямые совпадают)
ур-ние имеет бескон множ-во решений.
(прямые совпадают)
![]() и
и
![]()
2
случай:
,
![]() ,
т.е.
,
т.е.
![]() - ур-ние решений не имеет, т.к. прямые
параллельны.
- ур-ние решений не имеет, т.к. прямые
параллельны.
3
случай:
![]() ,
ур-ние имеет единственное реш, т.е. прямые
пересек в единственной точке.
,
ур-ние имеет единственное реш, т.е. прямые
пересек в единственной точке.
![]()
Вопрос №6.Линии второго порядка на плоскости.
Линии, ур-ния к-рых в прямоуг. с-ме координат задаются ур-нием 2-ой степени наз линиями 2-го порядка. К важнейшим линиям второго порядка относят эллипс, окружность, гиперболу, параболу.
Окружность. Эллипс.
Эллипсом наз множ-во всех точек плоскости, для каждой из к-рых сумма расст до двух данных точек, наз-мых фокусом, есть величина постоянная, большее, чем расст между фокусами.
П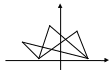 усть
усть
![]() имеет
корд.
имеет
корд.![]() ,
,
![]() Запишем расстояние
Запишем расстояние
![]() .
Пусть постоянная величина, фигурирующая
в определении эллипса = 2а
.
Пусть постоянная величина, фигурирующая
в определении эллипса = 2а
![]() ;
;
![]()
![]()
![]()
![]() (1)-
каноническое
ур-ние эллипса.
(1)-
каноническое
ур-ние эллипса.
Т очки
пересеч эллипса с осями коордт наз
вершинами эллипса, оси симметрии(Ох и
Оу) –осями эллипса. Осями также наз
отрезки
очки
пересеч эллипса с осями коордт наз
вершинами эллипса, оси симметрии(Ох и
Оу) –осями эллипса. Осями также наз
отрезки
![]() .
Отрезки
.
Отрезки
![]() и
и
![]() наз-ют полуосями. В нашем случае АВ,
-большая полуось ,
-малая
полуось. Эксцентриситетом
наз отношения фокусного расст к длине
большой оси и обозначают
наз-ют полуосями. В нашем случае АВ,
-большая полуось ,
-малая
полуось. Эксцентриситетом
наз отношения фокусного расст к длине
большой оси и обозначают
![]() .
т.к.
0,
то 1.
Фокальными радиусами точки М наз отрезки
.
т.к.
0,
то 1.
Фокальными радиусами точки М наз отрезки
![]() и
и
![]() ,
их длины равны.
,
их длины равны.
![]() .
Ур (1) можно рассм и в случае когда
.
В этом случае большая полуось
равны
.
Фокусы такого эллипса лежат на оси Оу
и
.
Ур (1) можно рассм и в случае когда
.
В этом случае большая полуось
равны
.
Фокусы такого эллипса лежат на оси Оу
и
![]() .
В случ, когда
=
получаем
ур
.
В случ, когда
=
получаем
ур
![]() ,
т.е. ур окр-ти.
,
т.е. ур окр-ти.
Окружность
-
частный случай эллипса при равенстве
полуосей. Для окружности![]() .Канон
ур-ние окр имеет вид
.Канон
ур-ние окр имеет вид
![]() ,
,
