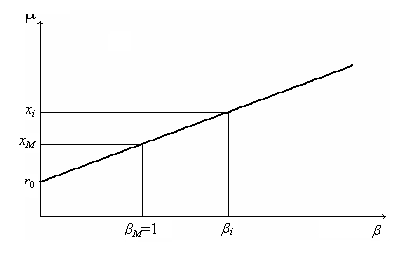
Модель ценообразования на рынке капитала (Capital Asset Pricing Model – capm)

• Основное уравнение CAPM:

,

где 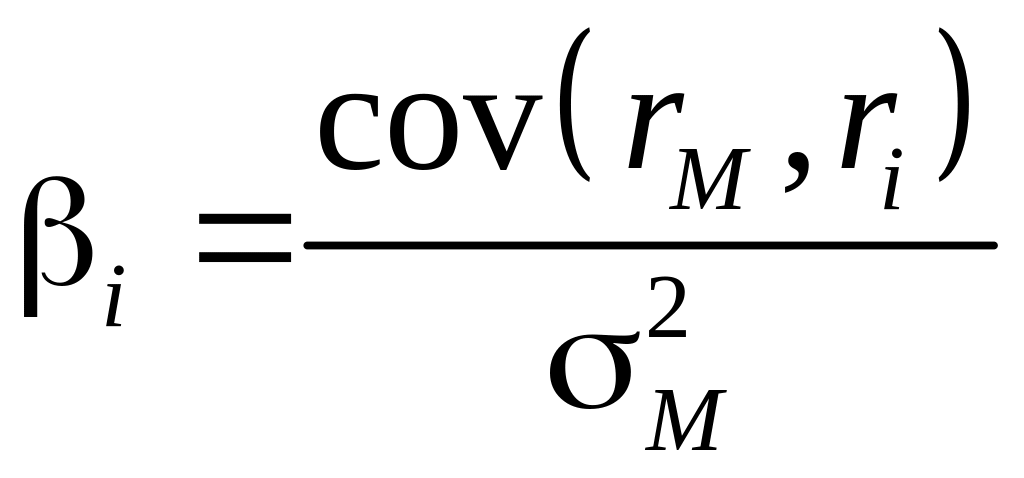- Бета ценной бумаги.

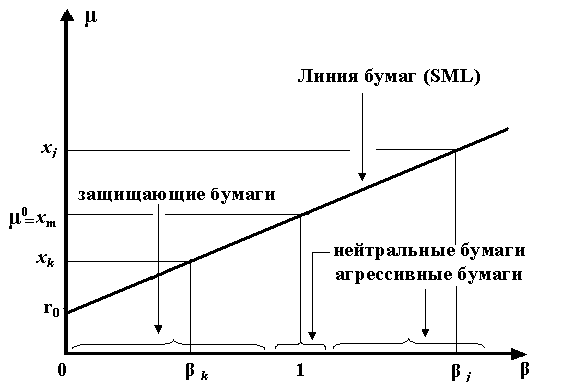
Рис. 5.3.Линия бумаг (SML – Security Market Line)

• Реальное соотношение:

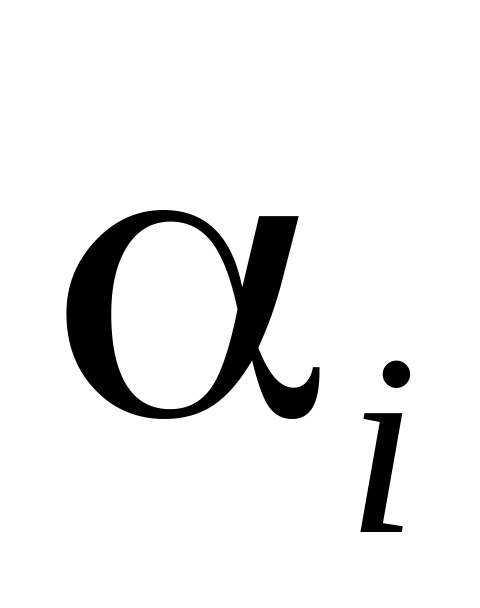• - Aльфа ценной бумаги.

Диверсифицируемый (устранимый, не систематический) и не диверсифицируемый (систематический) риск

Диверсифицируемый риск – это та часть общего риска ценной бумаги, которая может быть устранена при включении этой бумаги в эффективный портфель с той же доходностью. На Рис. 5.3 изображены риски и для двух бумаг, символами и обозначены диверсифицируемые (не систематические) риски данных бумаг, а символами и - систематические, не диверсифицируемые риски.

Рис. 5.3.Диверсифицируемые и не диверсифицируемые риски

Задачи с решениями

Задача 5.1. Для акций компании K известно значение . Предположим, что рынок находится в равновесии (является идеальным конкурентным), безрисковая процентная ставка равна 6%, ожидаемая доходность рыночного портфеля – 14%.

Вопрос: какова ожидаемая доходность акции K?

Решение.

Ожидаемая доходность акций определяется из основного уравнения CAPM:

.

Таким образом, ожидаемая доходность равна 18%.

Задача 5.2 Пусть в условиях идеального конкурентного рынка имеем два эффективных портфеля (решения задачи Тобина) со следующими характеристиками:

Портфель	А	B
Доходность - (%)	26	18
Стандартное отклонение (риск) - (%)	15	9

Вопрос: Найти безрисковую процентную ставку

Решение. Воспользуемся уравнением CML в форме

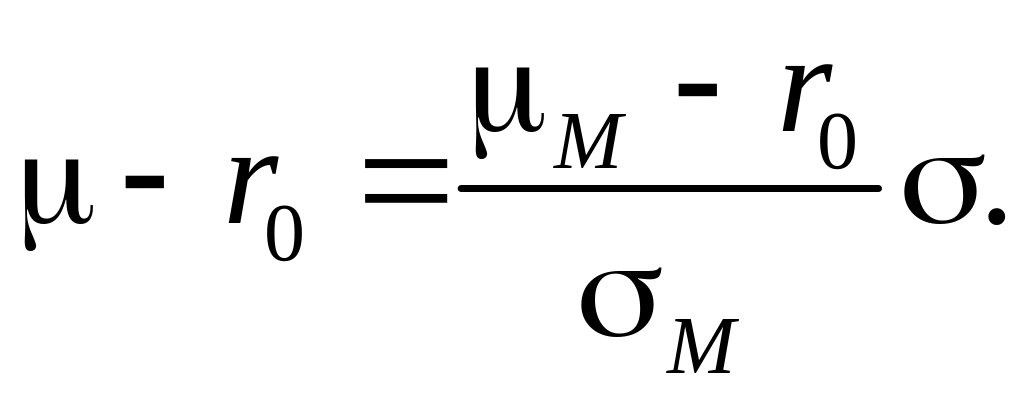
Из того, что оба портфеля являются эффективными, выводим

,

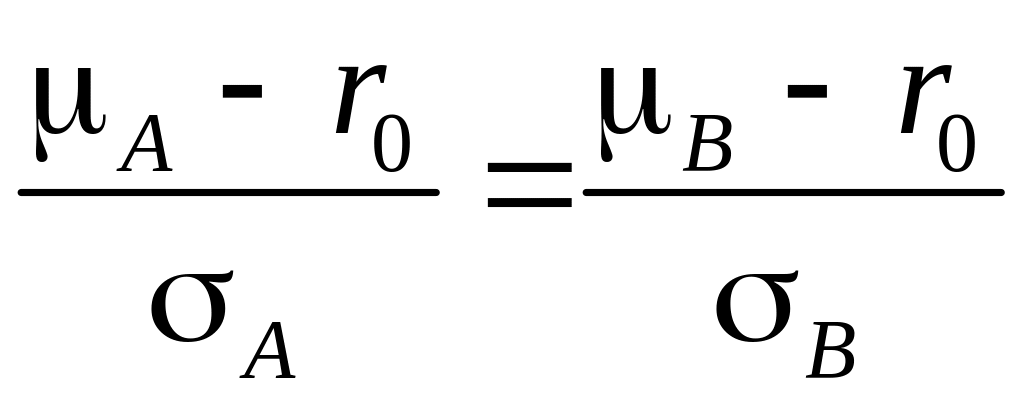откуда получаем

6 (%).

Задачи для самостоятельного решения

Задача 5.3 Рассмотрим идеальный конкурентный рынок. Безрисковая процентная ставка , ожидаемая доходность рыночного портфеля , стандартное отклонение рыночной доходности (рыночный риск) .

Вопросы :

а ) Рассчитать и изобразить линию рынка CML;

б) Рассмотреть три ценные бумаги, которые имеют следующие коэффициенты ковариаций с доходностью рынка:

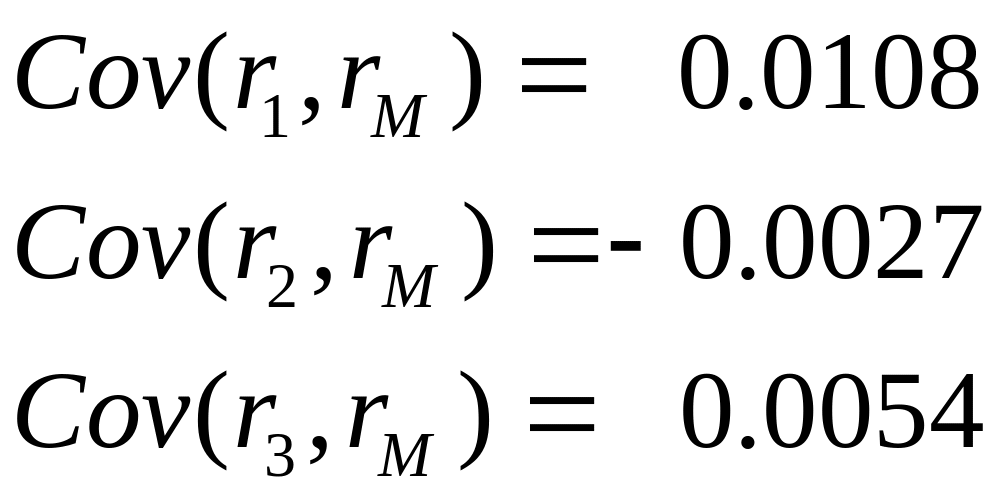
Изобразить линию бумаг SML и определить ожидаемые доходности данных бумаг; ,

в) Определить коэффициенты (Бета) указанных бумаг;

г) Приняв, что стандартные отклонения для бумаг равны соответственно и , определить диверсифицируемый риск каждой бумаги.

6. Введение в теорию опционов

Опцион – производная ценная бумага, удостоверяющая право на покупку (продажу) предмета контракта в будущем на заранее оговоренных условиях (по заранее оговоренной цене) или на отказ от сделки.

В настоящем разделе рассматриваются так называемые стандартные опционы CALL (КОЛЛ) и PUT (ПУТ).

Стандартные опционы CALL и PUT. Опцион CALL предоставляет держателю опциона право купить оговоренный в контракте актив в установленные сроки у продавца опциона по цене исполнения или отказаться от этой покупки.

Опцион PUT дает держателю опциона право продать оговоренный в контракте актив в установленные сроки продавцу опциона по цене исполнения или отказаться от его продажи.

Опционы, которые могут быть исполнены на протяжении определенного периода времени, называются американскими. Опционы, которые могут быть исполнены только в определенный момент времени, называются европейскими.

При покупке опциона покупатель уплачивает продавцу премию C.

Функция платежа – функция, описывающая выигрыш (проигрыш) владельца (держателя) опциона.

Для стандартного опциона CALL и опциона PUT функции платежа имеют вид:

, (6.1)

. (6.2)

Здесь K – заранее оговоренное число – цена исполнения, а S – цена базисного актива на момент исполнения.

Графически зависимость выигрыша владельца опциона CALL от цены базисного актива имеет вид:

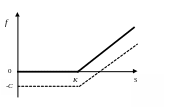
Рис. 6.1.Выигрыш покупателя опциона CALL

Здесь сплошной линии соответствует собственно выигрыш лица, уже имеющего опцион, а пунктиром – выигрыш с учетом суммы, уплаченной за приобретение опциона (премии).

Аналогично, график функции выигрыша держателя опциона PUT имеет вид, изображенный на Рис. 6.2.

Нетрудно построить и графики функций выигрыша продавцов CALL и PUT опционов.

Рис.6.2.Выигрыш покупателя опциона PUT

Графически выигрыш продавца опциона CALL имеет вид:

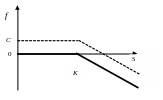
Рис. 6.3.Выигрыш продавца опциона CALL

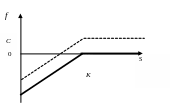
Рис. 6.4.Выигрыш продавца опциона PUT

На всех рисунках пунктирными линиями изображены функции платежей с учетом премии за опцион С.

Теорема о паритете PUT и CALL опционов. Существует теорема о паритете PUT и CALL опционов:

, (6.1)

где - цена опциона CALL, - цена опциона PUT, - цена исполнения опциона CALL, - цена базисного актива при , - безрисковая процентная ставка на период .

Определение цены опциона: однопериодная модель. Одна из главных задач, которую решает инвестор, - это определение цены опциона. Рассмотрим однопериодную (или одношаговую) модель определения цены опциона. В одношаговой модели значение опциона и цена базисного актива рассматриваются только в начале и в конце некоторого периода Т.

Примем следующие обозначения: - безрисковая процентная ставка, – известная цена базисного актива при , и неизвестные значения при (только два), и - выплаты по опционам, отвечающие этим значениям, . Предположим, что справедливы следующие соотношения:

, , (6.2)

, , (6.3)

, , (6.4)

где u – величина, характеризующая прирост стоимости базисного актива опциона, d – величина, характеризующая падение стоимости базисного актива, K – цена исполнения опциона.

Изменение цены можно представить следующим образом:

Безрисковый портфель. Один из способов определения цены опциона в рамках однопериодной модели – составление безрискового портфеля. Опишем этот способ.

Пусть портфель состоит из одного актива и проданных опционов CALL. При портфель стоит , при он может стоить или . Выберем k так, чтобы выполнялось условие:

, (6.5)

откуда

. (6.6)

При таком значении k получим одну и ту же сумму в начале и конце периода:

. (6.7),

Величина к называется коэффициентом хеджирования.

Из равенства (6.7) выражается цена опциона, которая имеет следующий вид:

, (6.8)

где

.

Общий подход к определению цены опциона. Существует общий подход к определению цены опциона. Рассмотрим его в рамках однопериодной модели.

К соотношениям (6.2) добавляется равенство

, (6.9)

характеризующее изменение стоимости безрискового актива. Общий подход состоит в следующем. Пусть инвестор при располагает начальным капиталом, который распределен между банковским счетом (облигациями) и рисковым активом (акциями):

. (6.10)

В момент инвестор перераспределяет свой капитал:

. (6.11)

Стратегией управления капиталом назовем пару , которая определяет перераспределение капитала. В момент времени инвестор имеет следующее значение капитала:

. (6.12)

Величина зависит от трех параметров: , так как , где

- случай.

Выплаты по опциону также зависят от случая:

.

Справедливой (рациональной) ценой опциона CALL называется минимальное значение капитала , который следует иметь продавцу опциона, чтобы выполнить обязательства по опциону, применяя подходящую стратегию U, независимо от того, какое событие реализовалось, т.е.:

.

Таким образом, приходим к следующей задаче линейного программирования:

Искомая цена опциона равна:

, (6.13)

где , а , 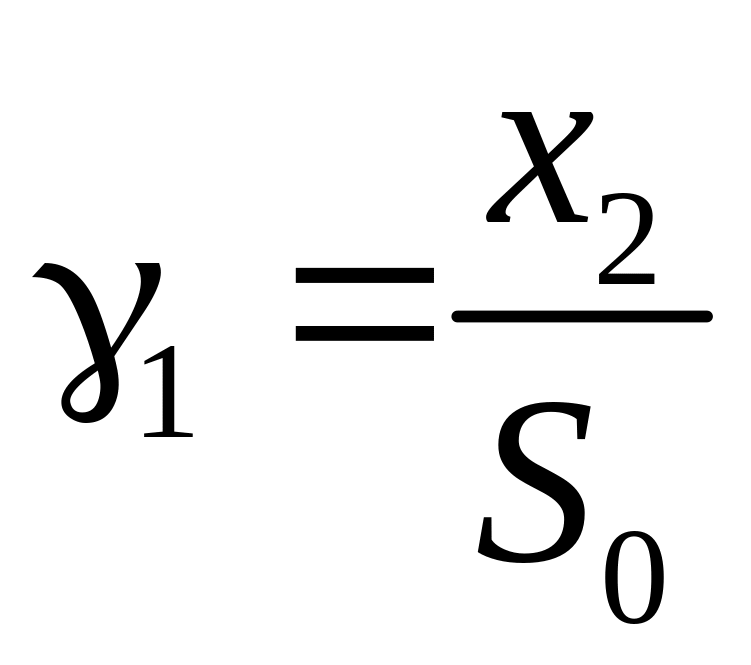- хеджирующая стратегия (хедж).

Многошаговая биномиальная модель. При многошаговой биномиальной модели осуществляется разбиение периода действия опционного контракта на ряд интервалов моментами времени . Динамика рискового актива имеет вид:

,

где задано. Характеристика безрискового актива имеет вид:

,

где задано.

Изменение цены на базисный актив можно представить с помощью дерева распределений:

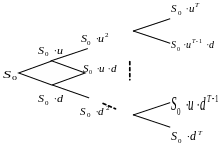
Рисунок 6.5.Динамика курса цены базисного актива для многошаговой модели

При определении цены опциона как минимального значения капитала , который следует иметь продавцу опциона, чтобы выполнить свои обязательства по опциону, приходим к следующей формуле для определения цены:

. (6.14)

После математических преобразований получим формулу расчета премии за опцион (формулу CRR):

,

где

. (6.15)

- функция Бернулли, которая показывает вероятность того, что в T независимых испытаниях события, вероятность осуществления которого равна , осуществляется не менее чем раз.

Эта формула получена в 1986 г. и носит название формулы Кокса-Росса-Рубенштейна.

Для того, чтобы определить следует воспользоваться формулами одношаговой модели, заменив в них на , на , на , р - то же самое.

Непрерывная модель. В 1973 году Ф.Блэком и М.Шоулсом была предложена формула расчета цены опциона CALL в условиях , когда динамика цены рискового актива описывается стохастическим дифференциальным уравнением. Эта формула стала знаменитой формулой Блэка-Шоулса:

,

где 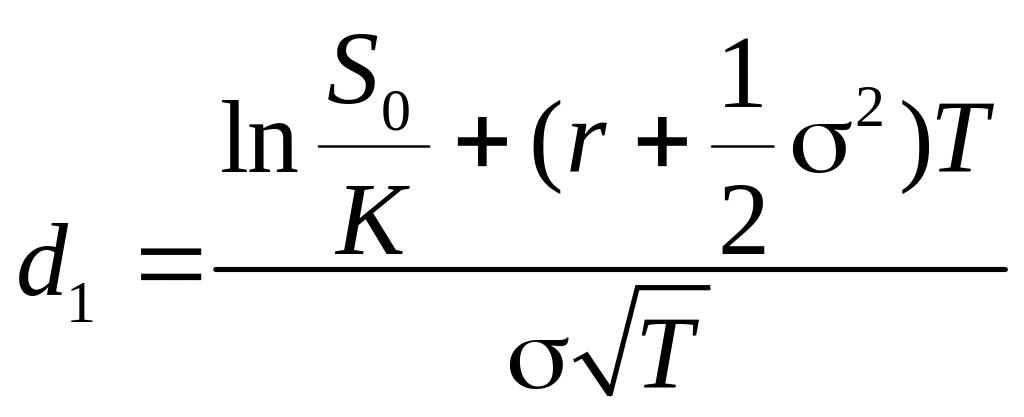, , - среднеквадратическое отклонение цены базисного актива, Т - период, - функция нормального распределения с параметрами 0 и 1.