15) Векторно-параметрическое уравнение прямой

где   - фиксированная точка, лежащая на прямой;   - направляющий вектор.

     В координатах (параметрические уравнения):

     Канонические уравнения прямой 

16) Уравнения прямой, проходящей через две данные точки

Пусть прямая проходит через две точки:  ,  направ­ляющим вектором такой прямой является вектор  , и уравнения   принимают вид:

 

Параметрические уравнения прямой

 Параметрические уравнения прямой

Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки   и направляющего вектора  , параллельного этой прямой.

Пусть прямая проходит через точку  , лежащую на прямой параллельно вектору  . Рассмотрим произвольную точку   на прямой. Очевидно, что  .

Так как векторы   и   коллинеарны, то найдется такое число  , что  , причем число   может принимать любое числовое значение в зависимости от положения точки   на прямой. Множитель   называется параметром.

Обозначив радиус-векторы точек   и   соответственно через   и  , получаем  . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра   соответствует радиус-вектор некоторой точки  , лежащей на прямой.

Так как векторы       то

.

Полученные уравнения называются параметрическими уравнениями прямой. При изменении параметра   изменяются координаты  и   и точка   перемещается по прямой.

Замечание. Если принять каждую из равных дробей в канонических уравнениях прямой   за некоторый параметр  ,  , то можно получить параметрические уравнения  .

17) Прямая как линия пересечения двух плоскостей

Пусть относительно ПДСК заданы две плоскости своими общими уравнениями, пересекающихся по некоторой прямой: α: A1x+B1y+C1z+D1=0. β: A2x+B2y+C2z+D2=0. Запишем канонические уравнения прямой, полученные в результате пересечения плоскостей α и β. Пусть x0, y0, z0 - какое-либо решение {A1x+B1y+C1z+D1=0. {A2x+B2y+C2z+D2=0. Точка M0(x0, y0, z0) принадлежит прямой пересечения плоскостей α и β. Покажем, что в качестве направляющего вектора прямой можно взять вектор a с координатами {B1 C1 C1 A1 A1 B1} {B2 C2,C2 A2,A2 B2}. В самом деле, в силу необходимого и достаточного условия компланарности вектора и плоскости имеем N1={A1, B1, C1}, N2={A2, B2, C2}. Так как определитель содержит две одинаковые строки, то направляющий вектор прямой, полученный в результате пересечения плоскостей α и β, компланарен плоскости α, а значит, и сама прямая компланарна плоскости α. Аналогично проверяем компланарность направляющего вектора прямой и плоскости β. Таким образом, вектор а можно выбрать в качестве направляющего вектора прямой, полученной в результате пересечения плоскостей α и β. Каноническое уравнение прямой имеет вид:

18) Параллельность, перпендикулярность прямых, угол между прямыми

Следует обратить внимание на то, что в числителе дроби из углового коэффициента второй прямой вычитается угловой коэффициент первой прямой.

Если уравнения прямой заданы в общем виде

A₁x + B₁y + C₁ = 0,         

A₂x + B₂y + C₂ = 0,     (6)

угол между ними определяется по формуле

     (7)

4. Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂.     (8)

б) Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

     (9)

5. Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

     (10)

Общее уравнение прямой:

 

Ах +  Ву +  С = 0 ,

 

где  А и В  не равны нулю одновременно.

Коэффициенты А и В являются координатами нормального вектора прямой ( т.е. вектора, перпендикулярного прямой ). При  А = 0  прямая параллельна оси ОХ , при  В = 0 прямая параллельна оси ОY .

При  В   0  получаем  уравнение прямой с угловым коэффициентом:

Уравнение прямой, проходящей через точку ( х₀ ,  у ₀ ) и не параллельной оси OY, имеет вид:

 

у – у ₀ = m ( x – х₀ ) ,

 

где  m  –  угловой коэффициент, равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ .

При  А   0,  В   0 и С   0  получаем  уравнение прямой в отрезках на осях:

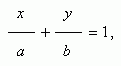
где  a = – C / A ,   b = – C / B . Эта прямая проходит через точки ( a, 0 ) и ( 0, b ), т.е. отсекает на осях координат отрезки длиной  a  и  b .

Уравнение прямой, проходящей через две различные точки ( х₁,  у ₁ ) и ( х₂,  у 2 ):

Параметрическое уравнение прямой, проходящей через точку ( х₀ ,  у ₀ ) и параллельной направляющему вектору прямой ( a, b ) :

Условие параллельности прямых:

  1)  для прямых  Ах+ Ву+ С = 0  и  Dх+ Eу+ F = 0 :   AE – BD = 0 ,

 

  2)  для прямых  у = m x+ k  и  у = p x+ q :   m = p .

Условие перпендикулярности прямых:

  1)  для прямых  Ах+ Ву+ С = 0  и  Dх+ Eу+ F = 0 :   AD + BE = 0 ,

  2)  для прямых  у = m x+ k  и  у = p x+ q :   m  p =  – 1 .

Расстояние между двумя точками ( x₁,  y ₁ ) и ( x₂ ,  y₂ ) :

                                                                           

Расстояние от точки ( х₀ ,  у ₀ ) до прямой  Ах+ Ву+ С = 0 :

Расстояние между параллельными прямыми  Ах+ Ву+ С = 0  и  Dх+ Eу+ F = 0 :

Угол    между прямыми:

19) Расстояние точки A(x₁, y₁) до прямой Ax + By + C = 0 есть длина перпендикуляра, опущенного из этой точки на прямую.

Она определяется по формуле

Правило. Чтобы определить расстояние точки A(x₁, y₁) до прямой Ax + By + C = 0, нужно привести уравнение прямой к нормальному виду, взять левую часть полученного уравнения и подставить в нее вместо текущих координат координаты данной точки. Абсолютная величина полученного числа и даст искомое расстояние:

Расстояние от точки до прямой есть всегда величина положительная. Кроме расстояния от точки до прямой, рассматривается еще так называемое отклонение точки от прямой.

Отклонение   данной точки от данной прямой есть расстояние от этой точки до прямой, которому приписывается знак плюс, если точка и начало координат находятся по разные стороны от прямой, и знак минус, если точка и начало координат находятся по одну сторону от прямой.

Расстояние от точки до прямой есть абсолютная величина отклонения этой точки от прямой.

20)

21) Точка пересечения прямой с плоскостью 

     В координатах:

где