лекции, учебные пособия / конспект лекций / Lekcii / Лекция 5 (Пустовой Д

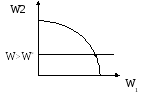Рассмотрим 2 критерия: W₁ и W₂:

W₁ – главный критерий.

Вводим ограничение по W₂, получаем точку максимального значения для W₁

Метод ранжирования критериев

W₁>W₂>W₃>…

Сначала проводят оптимизацию по первому критерию – получают некоторую ограниченную область, потом оптимизируют по следующему по важности критерию, далее сужая область.

Метод лексико-графической оптимизации

В данном методе используется принцип поиска слова в словаре.

Сначала критерии также ранжируются по важности.

W₁>W₂>W₃>…

a' > a”, если W₁’>W₁’’, где а – альтернатива

Если W₁’=W₁’’, то рассматриваем W₂ и т.д.

Метод последовательных уступок

Проводим ранжирование критериев как и раньше: W₁>W₂>W₃>…

Далее оптимизируем по наиболее важному критерию: Х₁^* = мах W₁(U)

Затем критерий W₁ переводим в ранг ограничений, ввобня некоторую уступку Δ. Находим решение.

Х₁^* = мах W₂(U)

W₁(U) >= X₁^* - Δ

Далее берём следующий критерий. Просмотрев все из них мы получим решение.

Δ

Есть метод при котором всё сводится к деньгам: рассматривается, например, 1 единицы памяти или производительности. Через денежный эквивалент одни параметры можно выразить через другие. Но не всё измеряется деньгами.

Принцип абсолютной уступки

Справедлив такой компромисс, при котором суммарный абсолютный уровень снижения одних критериев не превосходит оного для повышения других.

(аддитивный критерий)

Но данный критерий не всегда эффективен, например:

	W1	W2
I	0,9	0,2
II	1,0	0,1

В данном случае, казалось бы, что эти два решения одинаковы, но очевидно, что первое лучше, т.к. во втором мы улучшаем первый параметр на 10%, ухудшая второй на 50%.

Принцип относительной уступки

Справедлив следующий компромисс, при котором суммарный относительный уровень снижения качества одного или нескольких критериев не превосходит суммарный относительный уровень повышения качества по остальным критериям.

Сравним два решения: Е₀(е¹₀, е²₀, …, е^к₀) и Е₁(е¹₁, е²₁, …, е^к₁)

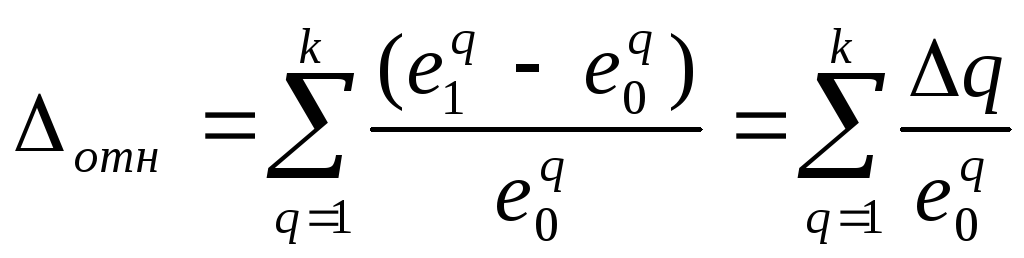
Если ∆_отн > 0, то решение Е1 лучше решения Е0

Если ∆_отн < 0, то решение Е0 лучше решения Е1

Оптимизацию проводим по следующему критерию:

Пример:

Рассмотрим два решения Е0(2,7) и Е1(3,5).

Тогда ∆_отн = (3-2)/2 + (5-7)/7 = 3/14 > 0 следовательно E1 лучше Е0

Аддитивный скалярный критерий

Пронормируем значения критериев, принимая, что все критерии равнозначны:

Проведём ранжирование критериев по параметру α_i.

Получаем следующий критерий оптимальности:

Пример:

X2

X2

. D – область компромиссов. Из рисунков очевидно, что данный критерий неприменим в случае невыпуклой области D.

D

D

X1

X1

Замечание: если критерий максимизирующий, то он берется со знаком (+), иначе – со знаком (-).

Мультипликативный скалярный критерий

Введём критерий

Проведём ранжирование

Замечание: если критерий максимизирующий, то он ставится в числитель, иначе – в знаменатель.

Мультипликативный критерий сводится к аддитивной форме:

Можно учесть и мультипликативный и аддитивный критерии сразу, задавая варьированием параметра β от 0 до 1 значимость каждого критерия в общей сумме.

Метод отклонения от идеала (целевое программирования)

Критерий качества решения – это его отклонение этого решения от некоторого идеального.

Пусть f_i0 – идеальное значение показателя, тогда критерий оптимизации выглядит следующим образом:

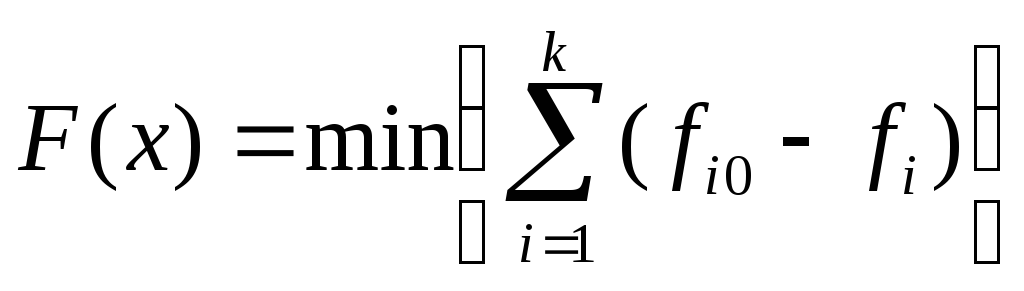
После нормировки получаем:

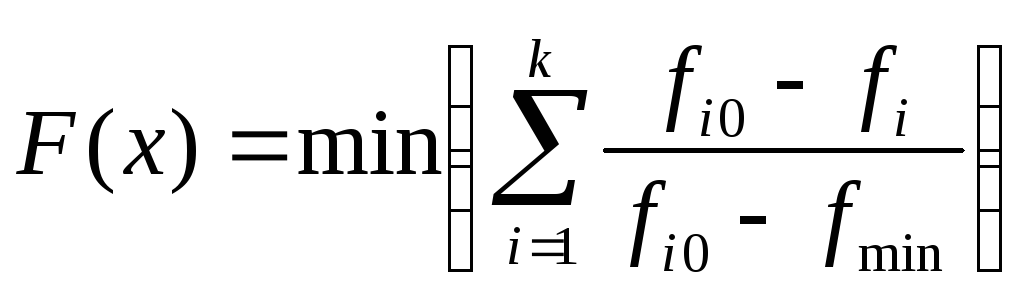
Учет ранга критериев вводится с помощью коэффициентов α_i, которые могут быть либо сомножителями, либо показателями степени.

Пример:

Дано три альтернативных решения:

f(x₁) = (10;10;3); f(x₂) = (8;8;10); f(x₃) = (0;0;0)

1 способ.

Пронормируем.

f(x1): (1;1;0,3) ∑ = 2,3

f(x2): (0,8;0,8;1) ∑ = 2,6

f(x3): (0;0;0) ∑ = 0

Очевидно, что лучшее решение номер два.

2 способ.

Т.к. решение 3 заведомо хуже первого и второго, можно его отбросить. После этого нормируем оставшиеся два решения:

f(x1): (1;1;0) ∑ = 2

f(x2): (0;0;1) ∑ = 1

На этот раз лучше решение номер один, что противоречит первому способу решения.