ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

ОТЧЕТ

По контрольной работе №1.

Вариант № 9.

по дисциплине «Эконометрика»

по учебному пособию «Эконометрика»

М. Г. Сидоренко, 2004г.

Контрольная работа № 1.

В соответствии с вариантом 9 на основе данных о доходах Y, расходах на продукты питания X₁, расходах на промышленные товары X₂, представленных в таблице 1,

Таблица 1

Y	X1	Вариант 9
		дети	X2
91,76	67,25	нет	3,95
38,68	22,95	нет	15,34
34,14	27,25	нет	0,39
30,77	12,84	нет	0,61
50,02	47,37	нет	1,60
34,33	21,78	есть	6,33
42,63	24,54	нет	8,14
63,47	58,61	есть	1,36
19,86	16,56	есть	2,44
58,87	44,77	есть	8,70
72,45	40,06	нет	3,87
29,70	20,87	есть	6,77
93,74	43,58	есть	29,33
17,77	16,88	есть	0,62
78,84	33,12	нет	11,01
39,73	30,99	есть	1,60
93,87	56,80	есть	15,75
86,15	48,19	есть	1,81
25,95	23,45	нет	2,30
36,95	18,88	есть	5,70
45,78	21,00	нет	14,79
12,36	12,01	есть	0,28

необходимо определить:

1. модель парной линейной регрессии вида Ŷ = b₀ + b₂X₂;

2. модель множественной линейной регрессии вида Ŷ = b₀ + b₁X₁+ b₂X₂;

3. линейно-логарифмическую модель вида Ŷ = b₀ + b₂lnX₂;

4. авторегрессионную модель вида Ŷ = b₀ + b₂X₂ +bY_t-1.

Для модели парной регрессии определить наличие гетероскедастичности (методом графического анализа остатков, при помощи теста ранговой корреляции Спирмена, теста Голдфелда-Квандта) и автокорреляции (графическим методом и при помощи критерия Дорбина-Уотсона).

Для всех моделей проверить качество уравнения регрессии, т.е.

• проверить статистическую значимость коэффициентов,

• определить интервальные оценки коэффициентов уравнения регрессии,

• определить доверительные интервалы для зависимой переменной,

• проверить общее качество уравнения регрессии (коэффициент детерминации и его статистическую значимость).

Сделать выводы о том, какая модель является наилучшей.

Задание 1. Определить модель парной линейной регрессии вида ;

Решение:

1. По выборке ограниченного объема мы сможем построить так называемое эмпирическое уравнение регрессии ŷ_i = b₀ + b₂x_i,

где ŷ_i - оценка условного математического ожидания M(Y׀X = x_i),

b₀ и b₂ – оценки неизвестных параметров β₀ и β₂, называемые эмпирическими

коэффициентами регрессии.

Для нашей задачи: y_i = b₀ + b₂x_i2, + e_i,

где отклонение e_i – оценка теоретического случайного отклонения ε_i.

Найдем оценки b₀ и b₂, используя метод наименьших квадратов по формулам:

b₂ = , b₀ = .

Данные и расчеты, необходимые для данных формул, представим в таблице 2:

Таблица 2

Данные варианта 9			Расчетные параметры
n						ŷi	ei	e
1	3,95	91,76	15,60	362,452	8419,90	45,36	46,40	2152,70	6,43	1752,26
2	15,34	38,68	235,32	593,35	1496,14	65,75	-27,07	732,55	78,39	125,8884
3	0,39	34,14	0,15	13,31	1165,54	38,99	-4,85	23,54	37,16	248,3776
4	0,61	30,77	0,37	18,77	946,79	39,39	-8,62	74,23	34,53	365,9569
5	1,6	50,02	2,56	80,03	2502,00	41,16	8,86	78,55	23,87	0,0144
6	6,33	34,33	40,07	217,31	1178,55	49,62	-15,29	233,84	0,02	242,4249
7	8,14	42,63	66,26	347,01	1817,32	52,86	-10,23	104,67	2,74	52,8529
8	1,36	63,47	1,85	86,32	4028,44	40,73	22,74	517,20	26,27	184,1449
9	2,44	19,86	5,95	48,46	394,42	42,66	-22,80	519,87	16,37	902,4016
10	8,7	58,87	75,69	512,17	3465,68	53,86	5,01	25,07	4,90	80,4609
11	3,87	72,45	14,98	280,38	5249,00	45,22	27,23	741,49	6,84	508,5025
12	6,77	29,7	45,83	201,07	882,09	50,41	-20,71	428,88	0,08	408,04
13	29,33	93,74	860,25	2749,39	8787,19	90,78	2,96	8,75	521,85	1921,946
14	0,62	17,77	0,38	11,02	315,77	39,40	-21,63	468,02	34,41	1032,337
15	11,01	78,84	121,22	868,03	6215,75	58,00	20,84	434,43	20,47	837,5236
16	1,6	39,73	2,56	63,57	1578,47	41,16	-1,43	2,04	23,87	103,4289
17	15,75	93,87	248,06	1478,45	8811,58	66,48	27,39	750,25	85,82	1933,361
18	1,81	86,15	3,28	155,93	7421,82	41,53	44,62	1990,66	21,86	1314,063
19	2,3	25,95	5,29	59,69	673,40	42,41	-16,46	270,93	17,52	573,6025
20	5,7	36,95	32,49	210,62	1365,30	48,49	-11,54	133,28	0,62	167,7025
21	14,79	45,78	218,74	677,09	2095,81	64,76	-18,98	360,29	68,96	16,9744
22	0,28	12,36	0,08	3,46	152,77	38,80	-26,44	698,82	38,51	1409,252
Сумма	142,69	1097,82	1996,99	9037,873	68963,73		0,00	10750,06	1071,51	14181,51
Средн.	6,49	49,90	90,77	410,81	3134,72
						ŷi	ei	e

b₂ = ==1,7895.

b₀ = =49,90-1,7874 x 6,49 = 38,2941.

Получаем уравнение парной регрессии: Ŷ = 38,2941 + 1,7895X₂.

По этому уравнению рассчитаем оценкуŷ_i условного математического ожидания M(Y׀X = x_i) и оценку e_i = - ŷ_i теоретического случайного отклонения ε_i, дополним этими расчетами приведенную выше таблицу 2.

2. Определим наличие гетероскедастичности.

a. Метод графического анализа остатков.

Построим график где по оси абсцисс отложим значения , а по оси ординат , взятые из столбцов таблицы 2.

Рисунок 1.

Из рисунка видно, что с увеличением уменьшается разброс значений , что свидетельствует об отсутствии гетероскедастичности.

b. Метод корреляции Спирмена.

Значения и из таблицы 2 упорядочим по величине, рассчитаем - разность между рангами и , определим и , результаты приведем в таблице 3.

Таблица 3

Исходные значения			Упорядоченные значения (по модулю)
i			ранг					разность рангов
1	3,95	46,4	1	0,28	1,43	2,04		-10	100
2	15,34	-27,07	2	0,39	2,96	8,75		2	4
3	0,39	-4,85	3	0,61	4,85	23,54		-1	1
4	0,61	-8,62	4	0,62	5,01	25,07		-2	4
5	1,6	8,86	5	1,36	8,62	74,23		0	0
6	6,33	-15,29	6	1,6	8,86	78,55		5	25
7	8,14	-10,23	7	1,6	10,23	104,67		9	81
8	1,36	22,74	8	1,81	11,54	133,28		-10	100
9	2,44	-22,8	9	2,3	15,29	233,84		-6	36
10	8,7	5,01	10	2,44	16,46	270,93		13	169
11	3,87	27,23	11	3,87	18,98	360,29		-8	64
12	6,77	-20,71	12	3,95	20,71	428,88		3	9
13	29,33	2,96	13	5,7	20,84	434,43		20	400
14	0,62	-21,63	14	6,33	21,63	468,02		-10	100
15	11,01	20,84	15	6,77	22,74	517,2		5	25
16	1,6	-1,43	16	8,14	22,8	519,87		6	36
17	15,75	27,39	17	8,7	26,44	698,82		1	1
18	1,81	44,62	18	11,01	27,07	732,55		-13	169
19	2,3	-16,46	19	14,79	27,23	741,49		-1	1
20	5,7	-11,54	20	15,34	27,39	750,25		5	25
21	14,79	-18,98	21	15,75	44,62	1990,66		8	64
22	0,28	-26,44	22	29,33	46,4	2152,7		-16	256
Сумма	142,69	0,00000							1670

Определим коэффициент ранговой корреляции по формуле:

= 1- 6 х = 0,057.

Рассчитаем статистику t по формуле:

= = 0,255.

Вывод: так как значение t меньше 2,086 то гипотеза отсутствия гетероскедастичности подтверждается с уровнем значимости α = 0,05. .

c. Тест Голдфелда-Квандта.

Упорядочим значения из таблицы 2 и поместим в столбец таблицы 3.

Всю упорядоченную выборку разбиваем на три подвыборки размерностей k, (n-2k), k. Определим k для n=22 исходя из пропорции n=30, k=11 в соответствии с рекомендациями Голдфелда и Квандта для парной регрессии. Получаем k=8.

Для первой и третьей подвыборки находим сумму:

i		i
1	2,04	15	517,2
2	8,75	16	519,87
3	23,54	17	698,82
4	25,07	18	732,55
5	74,23	19	741,49
6	78,55	20	750,25
7	104,67	21	1990,66
8	133,28	22	2152,7
Сумма	450,13	Сумма	8103,54

Определим дисперсию регрессии по первой и третьей выборке:

=450,13, = 8103,54.

S_{1 <<} S₃, это доказывает, что предположение о пропорциональности дисперсий отклонений значениям X₂ верно.

Находим соответствующую F- статистику: == = 18,003.

Определяем число степеней свободы для F- статистики, имеющей распределение Фишера: (где m – количество объясняющих переменных в уравнении регрессии, в нашей задаче m = 1), =20.

Из приложения 2 находим = ==1,79.

Если >, то гипотеза об отсутствии гетероскедастичности отклоняется с уровнем значимости α = 0,10, то есть подтверждается наличие гетероскедастичности.

Следовательно, по тестам графического анализа остатков и ранговой корреляции Спирмена подтверждается отсутствие гетероскедастичности, а по тесту Голдфелда-Квандта гипотеза об отсутствии гетероскедастичности отклоняется.

3. Определим наличие автокорреляции.

a. Графический метод.

Используя таблицу 2, построим график, откладывая по оси абсцисс порядковый номер наблюдения, а по оси ординат – оценки отклонений . Результаты представим на рисунке 2.

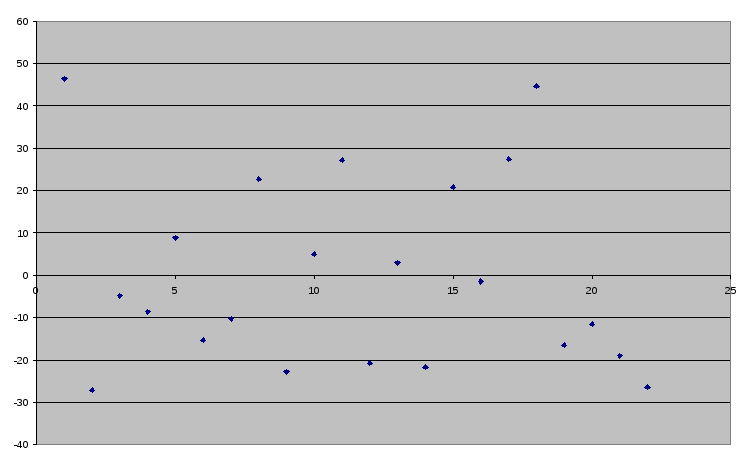
i

Рисунок 2.

Анализируя характер размещения точек на рисунке 2, можно сделать вывод об отсутствии зависимости между и порядковым номером наблюдения i, а следовательно, и об отсутствии автокорреляции.

2. Критерий Дарбина-Уотсона.

Представим дополнительные расчеты, необходимые для применения критерия Дарбина-Уотсона в таблице 4:

Таблица 4

i
1	46,4	2152,96
2	-27,07	732,78	-73,47	5397,841
3	-4,85	23,52	22,22	493,7284
4	-8,62	74,30	-3,77	14,2129
5	8,86	78,50	17,48	305,5504
6	-15,29	233,78	-24,15	583,2225
7	-10,23	104,65	5,06	25,6036
8	22,74	517,11	32,97	1087,021
9	-22,8	519,84	-45,54	2073,892
10	5,01	25,10	27,81	773,3961
11	27,23	741,47	22,22	493,7284
12	-20,71	428,90	-47,94	2298,244
13	2,96	8,76	23,67	560,2689
14	-21,63	467,86	-24,59	604,6681
15	20,84	434,31	42,47	1803,701
16	-1,43	2,04	-22,27	495,9529
17	27,39	750,21	28,82	830,5924
18	44,62	1990,94	17,23	296,8729
19	-16,46	270,93	-61,08	3730,766
20	-11,54	133,17	4,92	24,2064
21	-18,98	360,24	-7,44	55,3536
22	-26,44	699,07	-7,46	55,6516
Сумма		10750,48	-72,84	22004,47

==2,046.

Используя грубое правило для оценки по критерию Дарбина-Уотсона, можно сделать вывод, что автокорреляция остатков отсутствует.

4. Для проверки статистической значимости коэффициентов b₀ и b₂ рассчитаем оценку дисперсии S², стандартную ошибку оценки S, стандартные ошибки коэффициентов регрессии S_b0, S_b2:

S² = = = 537,503; S = = 23,18.

== 0,501; S_b2 = = 0,708.

= 90,77x0,501= 45,53; =6,75.

Проверим статистическую значимость коэффициентов b₀ и b₂ при помощи отношений t-статистики:

== 2,53.

== 5,67.

В случае , то статистическая значимость соответствующего коэффициента регрессии подтверждается. Критическое значение при уровне значимости α=0,05 (находим с использованием распределений Стьюдента - Приложение 1).

2,086, (так как n = 22 по таблице исходных данных).

Так как =2,53>2,086, то это подтверждает статистическую значимость коэффициента регрессии b₂. Аналогично для b₀.

Так как =5,67>2,086, то это подтверждает статистическую значимость и коэффициента регрессии b₀.

5. Интервальные оценки коэффициентов уравнения регрессии с надежностью 95% (α = 0,05) для b₀ и b₂ рассчитаем по формулам:

Для b₀ (38,2941- 2,086 х 6,75; 38,2941+ 2,086 х 6,75) = (24,2141; 52,3741).

Для b₂ (1,7895- 2,086 x 0,708; 1,7895 + 2,086 x 0,708) = (0,3127; 3,2663).

6. Определим доверительные интервалы для зависимой переменной. Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных объемов дохода при неограниченно большом числе наблюдений и уровне расхода на промышленные товары X₂ = 29,33. Принимаем x_p = X₂ и считаем по формуле:

38,2941+ 1,7895 x 29,33 2,086 x 23,18 x = 90,78 1,53.

Таким образом, интервал имеет вид: (92,31; 89,25).

7. Рассчитаем коэффициент детерминации по формуле:

Значение рассчитаем и сведем в столбце таблицы 2.

R² = 1 - = 0,242.

Коэффициент детерминации достаточно низкий (значительно меньше 1), что свидетельствует о низком качестве уравнения парной регрессии.

Задание 2. Определить модель множественной линейной регрессии вида

Ŷ = b₀ + b₁X₁+ b₂X₂;

• проверить статистическую значимость коэффициентов,

• определить интервальные оценки коэффициентов уравнения регрессии,

• определить доверительные интервалы для зависимой переменной,

• проверить общее качество уравнения регрессии (коэффициент детерминации и его статистическую значимость).

Решение: