
- •Предел и непрерывность функции одной переменной
- •2. Окрестности конечной точки и бесконечности
- •3. Определение предела функции
- •3.1. Предел функции на языке окрестностей
- •Если для такое, чтодля3.2. Предел функции на языке неравенств
- •3.3. Предел последовательности
- •5. Бесконечно малые функции
- •5.1. Определение и основные свойства
- •5.2. Отношение бесконечно малых. Неопределенность
- •5.3. Первый замечательный предел
- •5.4. Сравнение бесконечно малых
- •6. Бесконечно большие функции
- •6.1. Определение и основные свойства
- •6.2. Неопределенности
- •6.3. Неопределенность . Второй замечательный предел
- •7. Непрерывные функции
- •7.1. Функции, непрерывные в точке
- •7.2. Точки разрыва функции и их классификация
- •7.3. Функции, непрерывные на отрезке
- •Дифференциальное исчисление функции
- •Дифференцируемые функции. Дифференциал
- •8.4. Связь между непрерывностью и дифференцируемостью
- •8.5. Производная суммы, произведения, частного
- •8.6. Производная сложной функции
- •8.7. Логарифмическое дифференцирование
- •8.13. Дифференциалы высших порядков
- •9.2. Правило Лопиталя
- •9.3. Формула Тейлора
- •9.4. Асимптотические разложения
- •10.3. Наибольшее и наименьшее значение функции на отрезке
- •10.4. Выпуклость и вогнутость. Точки перегиба
- •10.5. Асимптоты графика функции
- •Свойства неопределенного интеграла
- •13. Основные методы интегрирования
- •13.1. Метод подведения под знак дифференциала
- •Метод замены переменной
- •Метод интегрирования по частям
- •14. Интегрирование некоторых классов функций
- •14.2. Интегрирование функций, содержащих квадратный трехчлен
- •14.3. Интегрирование дробно-рациональных функций
6.2. Неопределенности
Рассмотрим
функции
![]() Эти функции являются бесконечно большими
при
Эти функции являются бесконечно большими
при![]() ,
а функции
,
а функции![]() являются бесконечно малыми при
являются бесконечно малыми при![]() .
.
1).
Так как
![]() ,
топредел
отношения двух бесконечно
больших функций
может быть любым; его называют
неопределенностью вида
,
топредел
отношения двух бесконечно
больших функций
может быть любым; его называют
неопределенностью вида![]()
2).
Так как
![]() то предел произведения бесконечно
большой функции на бесконечно малую
может быть любым; его называют
неопределенностью вида
то предел произведения бесконечно
большой функции на бесконечно малую
может быть любым; его называют
неопределенностью вида![]() .
.
3).
Так как
![]() ,
то предел разности двух бесконечно
больших функций одного знака может быть
любым; его называют неопределенностью
вида
,
то предел разности двух бесконечно
больших функций одного знака может быть
любым; его называют неопределенностью
вида![]() .
.
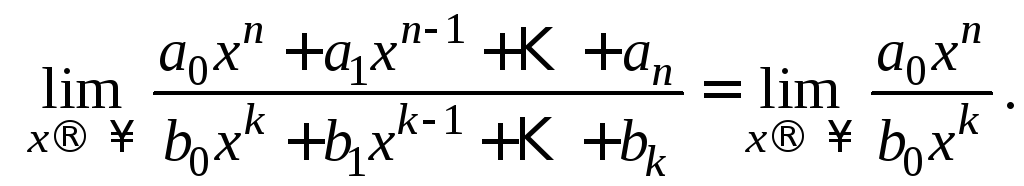
6.3. Неопределенность . Второй замечательный предел
![]() .
.
Число
e – иррациональное,
![]()
Это
соотношение будет справедливо, если
заменить натуральное число
![]() на действительное число
на действительное число![]() или на действительное число
или на действительное число![]() :
:
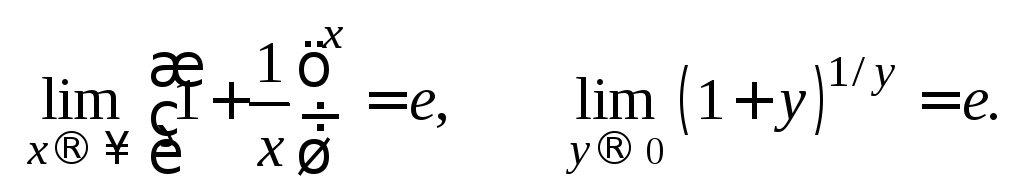
7. Непрерывные функции
7.1. Функции, непрерывные в точке
Пусть
функция
![]() определена в конечной точке
определена в конечной точке![]() и её окрестности.
и её окрестности.
|
Функция
|
Рассмотрим свойства функций, непрерывных в точке.
Теорема 7.1 (о приращении непрерывной функции).
Функция
![]() непрерывна в точке
непрерывна в точке![]() тогда и только тогда, когда
бесконечно малому приращению аргумента
соответствует бесконечно малое приращение
функции в точке
тогда и только тогда, когда
бесконечно малому приращению аргумента
соответствует бесконечно малое приращение
функции в точке![]() .
.
Теорема 7.2 (о непрерывности суммы, произведения, частного).
Сумма, разность, произведение конечного числа непрерывных в точке функций есть функция непрерывная в этой точке.
Частное непрерывных в точке функций есть функция, непрерывная в этой точке, если знаменатель в этой точке отличен от нуля.
|
Теорема 7.3 (о непрерывности сложной функции).
Пусть
функция
а)
сложная функция
б)
|
Пусть
задана функция
![]() с областью определения
с областью определения![]() и множеством значений
и множеством значений![]() .
Если каждому
.
Если каждому![]() поставить в соответствие
поставить в соответствие![]() такое, что
такое, что![]() ,
то это соответствие определяет функцию,
называемуюобратной к функции
,
то это соответствие определяет функцию,
называемуюобратной к функции![]() и обозначаемую
и обозначаемую![]() .
.
Область
определения
![]() обратной функции
обратной функции
![]() совпадает с множеством значений
совпадает с множеством значений
![]() функции
функции![]() :
:
![]() .
Множество значений
.
Множество значений
![]() обратной функции
обратной функции
![]() совпадает с областью определения функции
совпадает с областью определения функции
![]() :
:![]() .
Для отыскания функции, обратной к функции
.
Для отыскания функции, обратной к функции![]() ,
нужно выразить
,
нужно выразить![]() из уравнения
из уравнения![]() .
.
Функцию
![]() назовем непрерывной на интервале
назовем непрерывной на интервале![]() ,
если она непрерывна в каждой точке этого
интервала.
,
если она непрерывна в каждой точке этого
интервала.
Напомним,
что функция
![]() строго монотонна на интервале
строго монотонна на интервале![]() ,
то есть строго возрастает (соответственно
строго убывает) на интервале
,
то есть строго возрастает (соответственно
строго убывает) на интервале![]() ,
если для любых двух точек
,
если для любых двух точек![]() из этого интервала из неравенства
из этого интервала из неравенства![]() следует неравенство
следует неравенство![]() (соответственно
(соответственно![]() ).
).
Теорема 7.4 (о непрерывности обратной функции).
Пусть
функция
![]() строго монотонна и непрерывна на
интервале
строго монотонна и непрерывна на
интервале![]() .
Тогда существует обратная функция
.
Тогда существует обратная функция
![]() ,
которая будет монотонной и непрерывной
на интервале с концами
,
которая будет монотонной и непрерывной
на интервале с концами
![]() .
.
Теорема 7.5 (о непрерывности элементарной функции).
Если
элементарная функция определена в точке
![]() и её окрестности, то она непрерывна в
этой точке.
и её окрестности, то она непрерывна в
этой точке.
7.2. Точки разрыва функции и их классификация
Из
определения функции
![]() ,
непрерывной в точке
,
непрерывной в точке![]() ,
следует, что
,
следует, что![]() .
Это равенство означает выполнение трех
условий:
.
Это равенство означает выполнение трех
условий:
функция
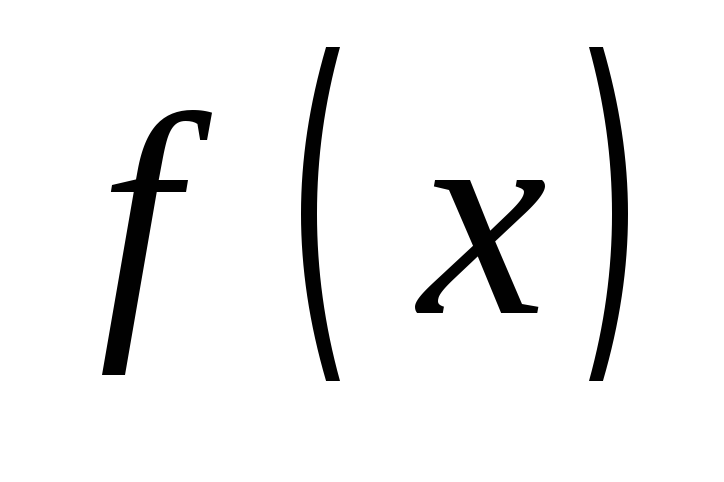 определена в точке
определена в точке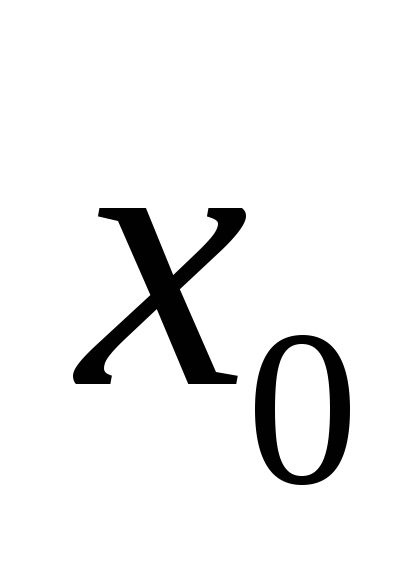 и ее окрестности,
и ее окрестности,функция
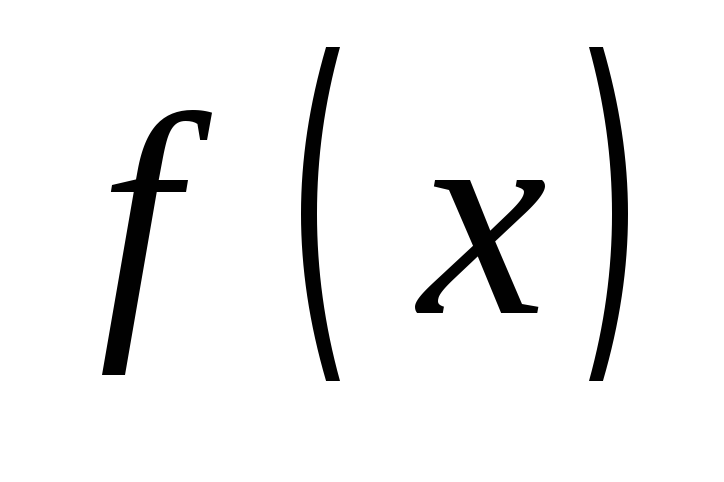 имеет предел при
имеет предел при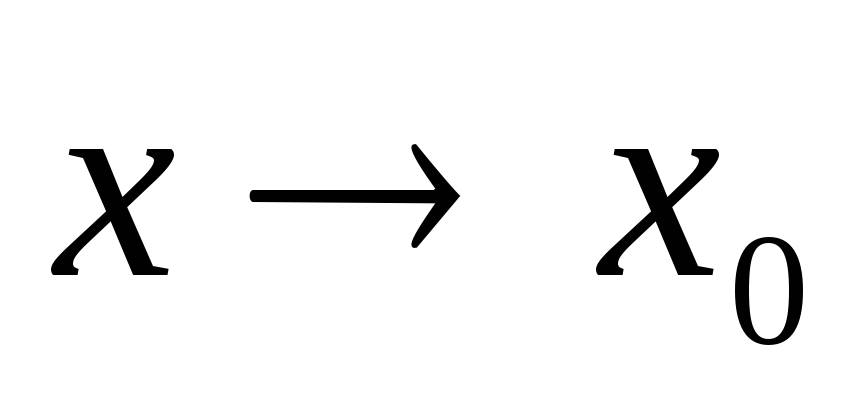 или, что равносильно, существуют и равны
односторонние пределы
или, что равносильно, существуют и равны
односторонние пределы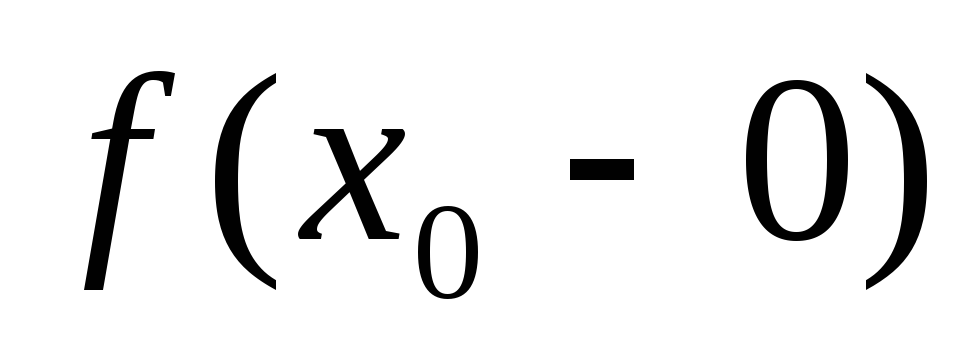 и
и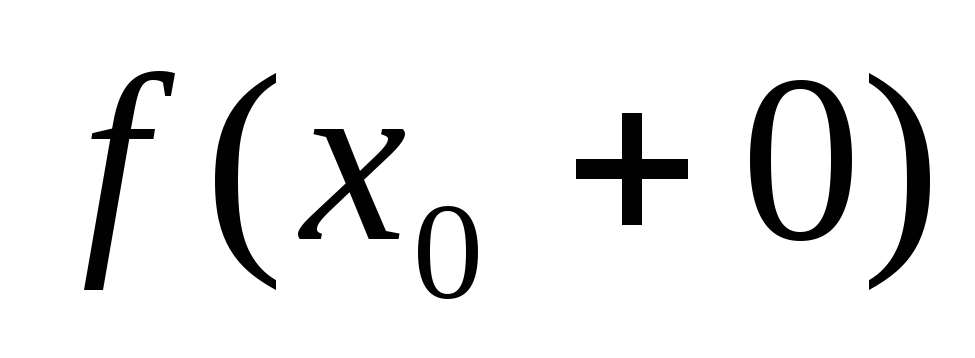 ,
,предел функции
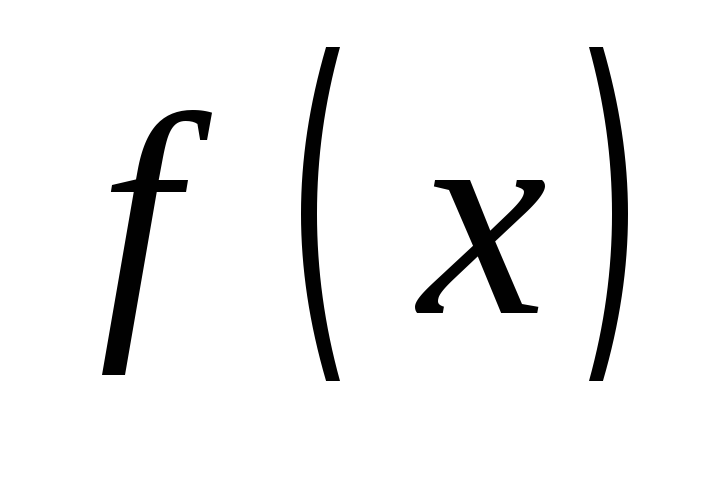 при
при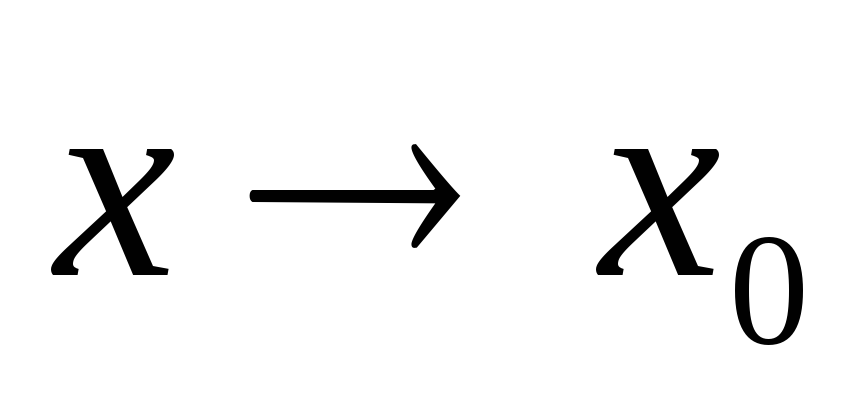 равен значению функции в точке
равен значению функции в точке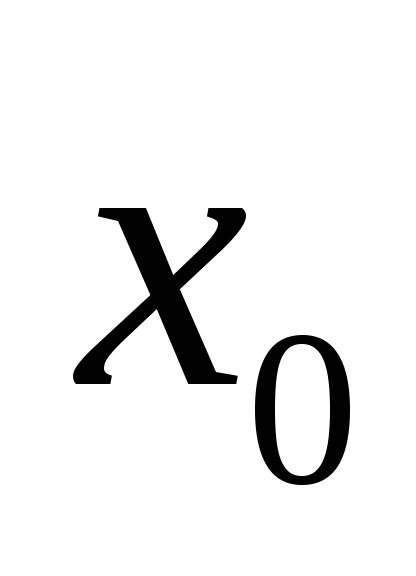 .
.
Если
нарушается хотя бы одно из этих условий,
то точку
![]() называютточкой разрыва функции.
Выделяют следующие типы точек разрыва.
называютточкой разрыва функции.
Выделяют следующие типы точек разрыва.
Если в точке разрыва
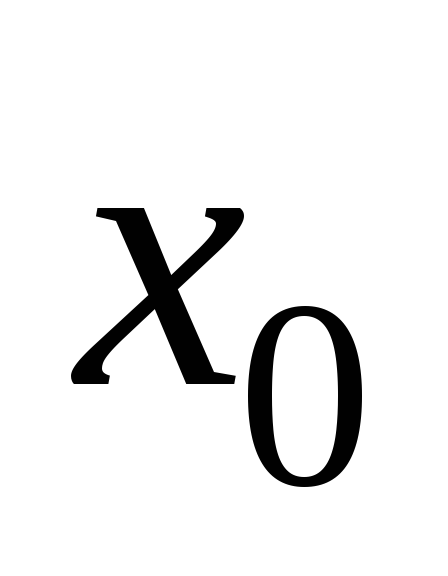 существуютодносторонние конечные
пределы функции, то
существуютодносторонние конечные
пределы функции, то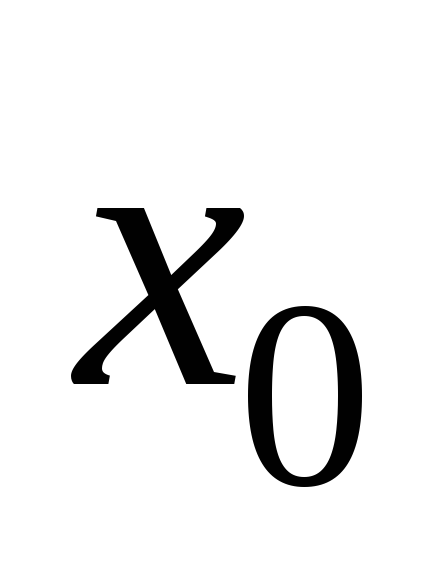 называют точкойразрыва первого
рода. При этом,
называют точкойразрыва первого
рода. При этом,
а)
если односторонние пределы совпадают,то![]() называют
называют
точкой устранимого разрывапервого рода,
б)
если односторонние пределы не
совпадают,то![]() называют
называют
точкой конечного разрывапервого рода (или точкой скачка).
Если в точке
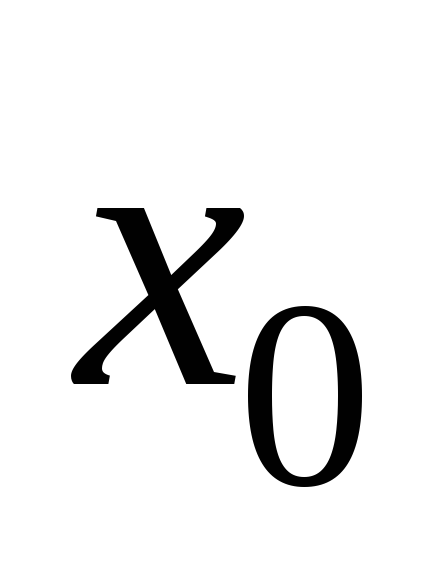 хотя бы один из односторонних пределов
функции
хотя бы один из односторонних пределов
функции
не
существует или бесконечен,
то ![]() называют точкой разрыва
второго рода.
называют точкой разрыва
второго рода.
