8.4. Связь между непрерывностью и дифференцируемостью

Если функция дифференцируема, то она непрерывна.

Действительно, для дифференцируемой функции . Отсюда следует, что бесконечно малому приращению аргументасоответствует бесконечно малое приращение функции, то есть, функциянепрерывна.

Непрерывная функция может не быть дифференцируемой.

8.5. Производная суммы, произведения, частного

Отыскание производных непосредственно по определению неудобно и сложно. Для этого существуют ряд правил и формул.

Теорема 8.2.Пусть функции− дифференцируемы. Тогда сумма, разность, произведение этих функций, а прии частное, будут дифференцируемы, причем

, ,.

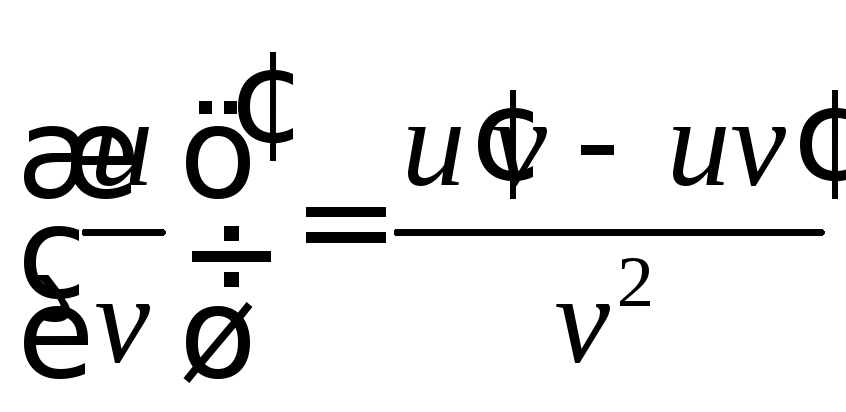Дифференциалы суммы, произведения, частного дифференцируемых функций вычисляются по формулам:

, ,.

8.6. Производная сложной функции

Пусть , а. Тогдасложная функция с промежуточным аргументом, независимым аргументом.

Теорема 8.3.Пусть функциядифференцируема в точке, а функциядифференцируема в соответствующей точке. Тогда сложная функциядифференцируема в точкеи для ее производной справедлива формула:.

Итак, для нахождения производной сложной функции надо производную функции по промежуточному аргументу умножить на производную промежуточного аргумента по независимому аргументу.

Это правило остается в силе, если промежуточных аргументов несколько.

8.7. Логарифмическое дифференцирование

В ряде случаев для нахождения производной функции удобно равенствосначала прологарифмировать, а затем продифференцировать. Такой прием называют логарифмическим дифференцированием. Его полезно применять для дифференцирования произведения многих сомножителей или для дифференцирования частного, числитель и знаменатель которого содержит несколько множителей, или для дифференцирования степенно-показательных функций. При этом следует учесть, что функциясложная, так каки поэтому.

8.8. Производная обратной функции

Теорема 8.4.Пусть функциястрого монотонна и дифференцируема на интервале, причем. Тогда обратная функциядифференцируема и ее производная вычисляется по формуле.

8.9. Гиперболические функции и их производные

В математике, механике, электротехнике используются гиперболические синус, косинус, тангенс и котангенс, определяемые следующим образом:

Отметим следующие свойства гиперболических функций:

8.10. Таблица производных

Рассмотренные правила и формулы дифференцирования запишем в виде таблицы.

Правила дифференцирования

1. ,

2. , в частности,, где с − число,

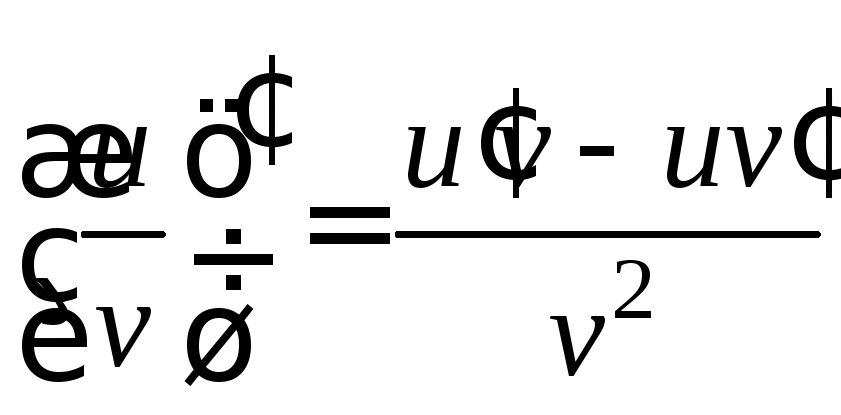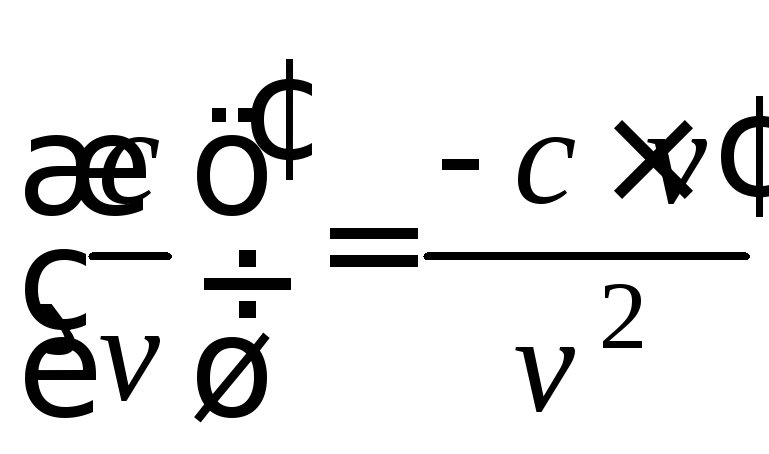3. , в частности,, где с − число,

4. , где,

5. .

Формулы дифференцирования

1. , в частности,;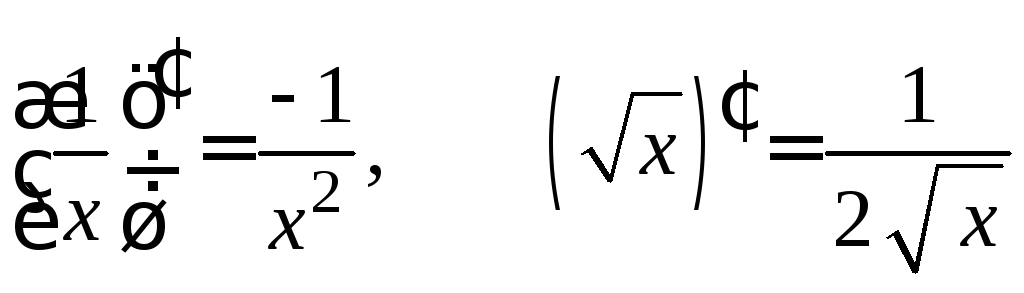

2. , в частности,;

3. , в частности,;

4. ;

5. ;

6. ;

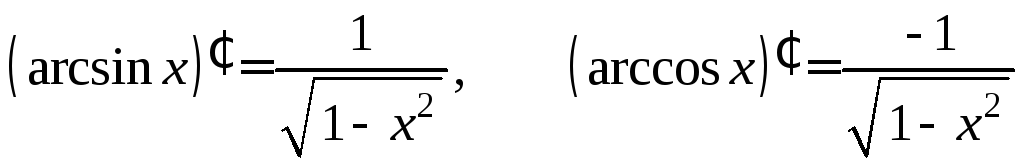7. ;

8. .

8.11. Производные высших порядков

Пусть − дифференцируемая функция. Производнаятакже является функцией от. Ее производная, если она существует, называется производной второго порядка и обозначается, или, или. Аналогично,,… Производной−го порядка функции называется производная от производной−го порядка:

.

8.12. Функции, заданные параметрически, и их производные

Пусть зависимость между аргументом и функциейзадана при помощи уравнений

,

где вспомогательная переменная, называемая параметром.

Будем предполагать, что функция имеет обратную функцию. Тогда равенства (8.5) определяют сложную функциюаргумента, заданную параметрическими уравнениями (8.5).

Теорема 8.5.Пусть функциязадана параметрическими уравнениями, гдедифференцируемые функции, причеми функцияимеет обратную. Тогда функция─ дифференцируема, а ее производная находится по формуле:.

Если при этом функции дважды дифференцируемы, то существует производная второго порядка, причем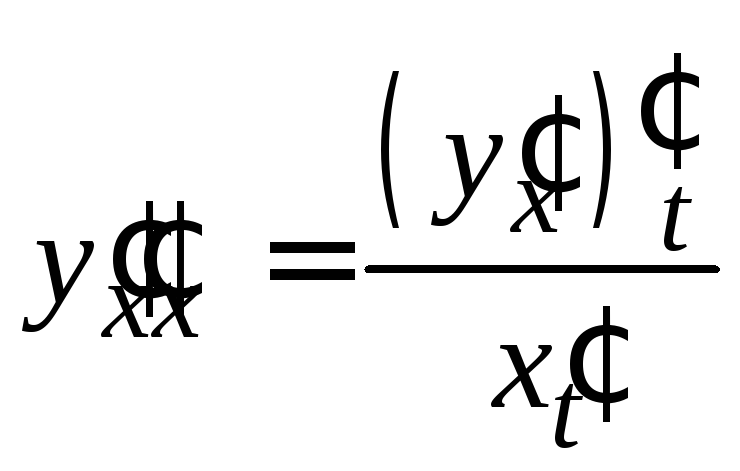.