7.3. Функции, непрерывные на отрезке

Функцияназывается непрерывной на отрезке, если

непрерывна в любой точке , т.е.

непрерывна в точке асправа, т.е.

непрерывна в точке bслева, т.е.

Непрерывные на отрезке функции имеют ряд важных свойств. Сформулируем их в виде теоремы, не приводя доказательство.

Теорема 7.6.Пусть функциянепрерывна на отрезке. Тогда:

1) функция ограничена на отрезке,

2) функция достигает на отрезкесвоего наибольшего и наименьшего значения,

3) функция принимает на отрезкевсе промежуточные значения между наибольшим и наименьшим,

4) если на концах отрезка функция принимает значения разных знаков, то на интерваленайдется хотя бы одна точка, в которой функцияпринимает нулевое значение.

Дифференциальное исчисление функции

одной переменной

Дифференциальное исчисление функции одной переменной изучает одно из основных математических понятийпонятие производной и ее применение, в частности, для исследования функций.

8. Производная и дифференциал

Понятие производной широко используется при решении целого ряда задач математики, физики, других наук, в особенности при изучении скорости протекания различных процессов.

8.1. Определение производной

Рассмотрим функцию . Придадим аргументуприращение. Тогда функцияполучит приращение, которое характеризует изменение функциина отрезке. Средняя скорость изменения функции на этом отрезке равна, а скорость изменения функциив точкеесть. Этот предел, если он существует, называется производнойфункциив точке. Итак, по определению

Для функции приняты и другие обозначения производной:.

8.2. Геометрический и физический смысл производной

Рассмотрим на кривой точкии секущую. При движении точкипо этой кривой к точкесекущаязаймет свое предельное положение.

Касательнойк данной кривой в точкеназывается прямая, являющаяся предельным положением секущейпри стремлении точкипо кривой к точке.

Н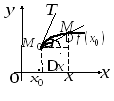айдем угловой коэффициентневертикальной секущей и угловой коэффициентневертикальной касательной:

,

.

Из этого равенства вытекает геометрический смысл производной.

Значение производной равно угловому коэффициенту касательной, проведенной к кривойв точкес абсциссой:.

Прямая, проходящая через точку касания перпендикулярно касательной к кривой, называется нормалью к этой кривой. Угловой коэффициент нормали

.

Уравнение касательнойк кривойв точкеимеет вид:

, где .

Уравнение нормалик кривойв точкеимеет вид:

.

Физический смыслпроизводной заключается в том, что значение производнойесть скорость изменения функциив точке. Поэтому

1. если задан закон движения материальной точки по прямой 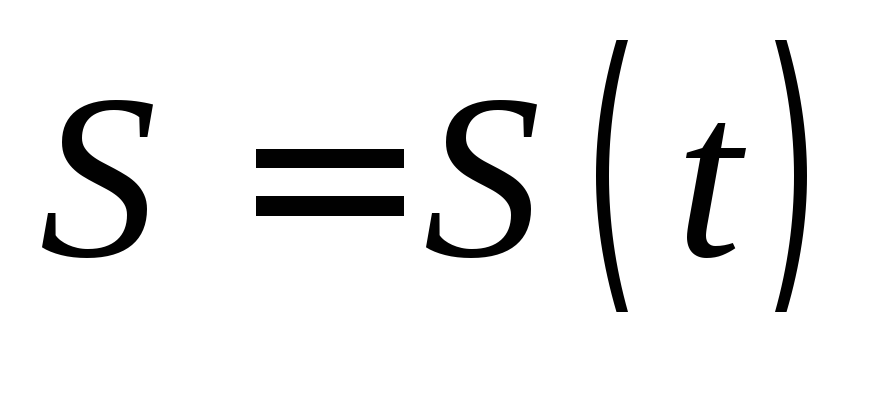, то скорость движения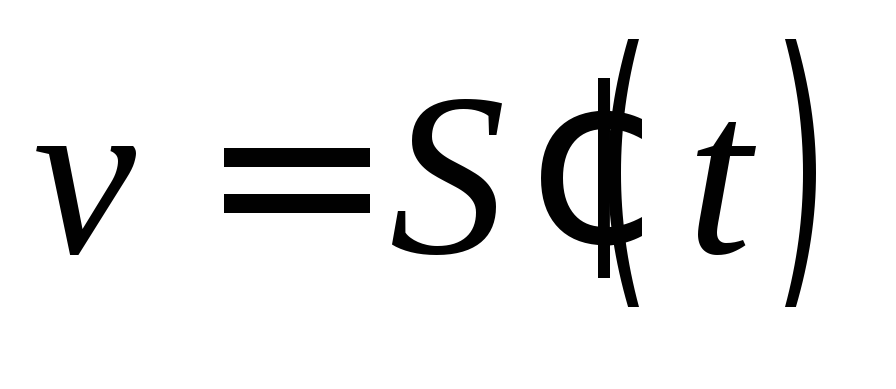, а ускорениеесть «скорость изменения скорости», то есть;

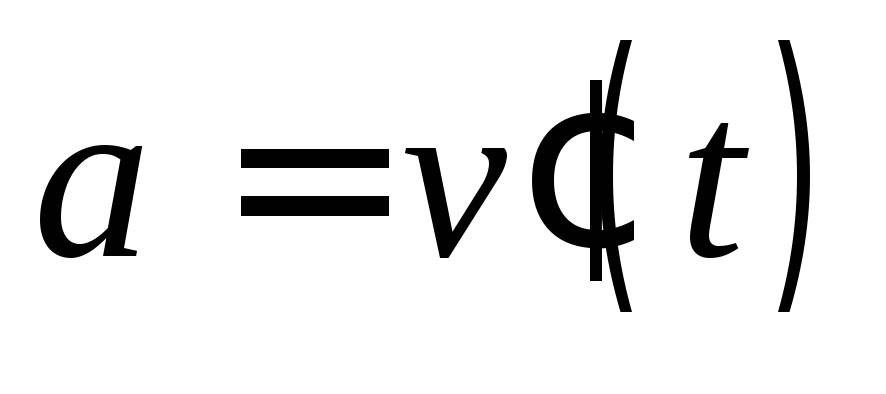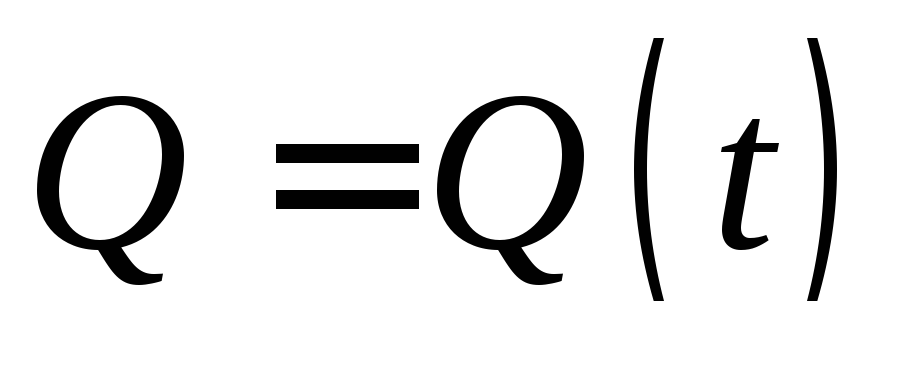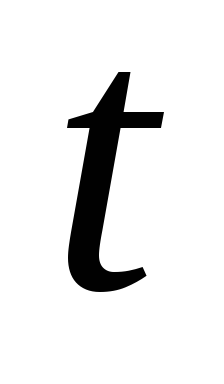2. если есть количество электричества, проходящего через поперечное сечение проводника за время, то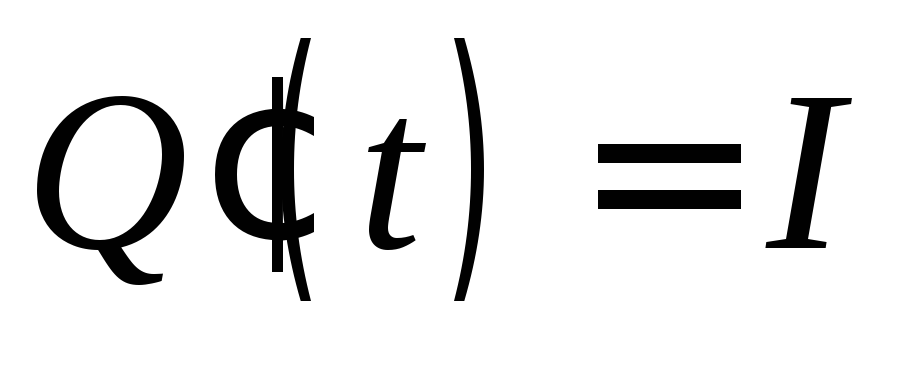есть сила тока ;

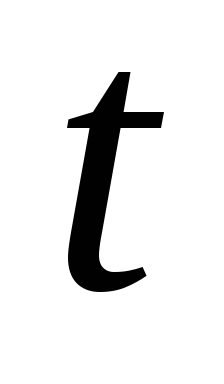3. если есть количество вещества, вступающего в химическую реакцию за время, тоесть скорость химической реакции.

8. Дифференцируемые функции. Дифференциал

Функция называетсядифференцируемой в точке, если ее приращениепредставимо в виде:,где не зависит от, а функцияявляется бесконечно малой при

Линейная относительно часть приращения функции называетсядифференциалом функции и обозначается, то есть.

Справедлива следующая теорема.

Теорема 8.1.Функциядифференцируема в точкетогда и только тогда, когда существует конечная производная; при этом.

, .