9.4. Асимптотические разложения

элементарных функций

.

.

.

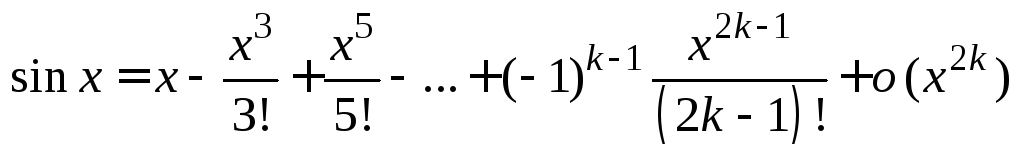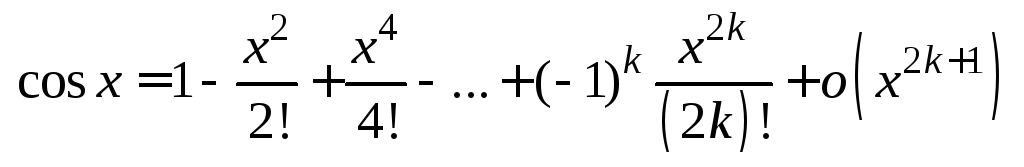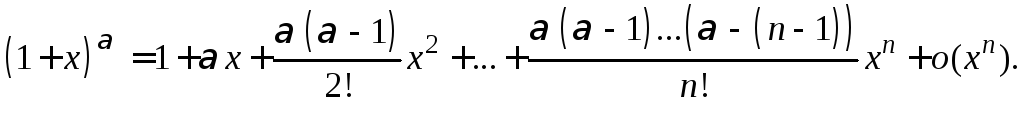
10. Исследование функций с помощью производной

Одним из приложений производной является применение производной к исследованию функции и построению графика функции. Мы рассмотрим такие характеристики функции, как монотонность, экстремум, выпуклость, а также асимптоты графика функции.

10.1. Монотонность функции

К монотонным функциям относятся функции, возрастающие или убывающие на промежутке. Напомним, что функция возрастает (соответственно убывает) на интервале , если для любых точекиз этого интервала из неравенстваследует неравенство(соответственно).

Теорема 10.1 (критерий монотонности).

Дифференцируемая функция возрастает (соответственно убывает) на интервалетогда и только тогда, когда(соответственно) на интервале.

10.2. Экстремумы функции

Пусть функция непрерывна на интервале, содержащем точку. Напомним ряд определений.

1). Точка называетсяточкой максимум функции, еслидля всехиз некоторой выколотой окрестности точки.

2). Точка называетсяточкой минимумафункции, еслидля всехиз некоторой выколотой окрестности точки.

3). Точки максимума и минимума функции называют ее точками экстремума.

.

Теорема 10.2 (необходимое условие экстремума).

Пусть функция имеет экстремум в точке. Тогда производнаяв точкеравна нулю или не существует.

Точки экстремума, в которых , назовемточками гладкого экстремума. В таких точках касательная к графику функции параллельна оси

1. . Точки экстремума, в которых 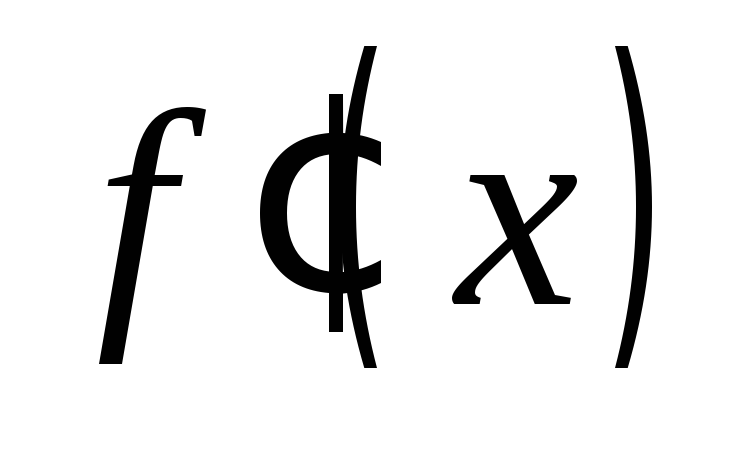не существует, назовемточками острого экстремума.

2. . Точки, в которых производная функции равна нулю или не существует, называют критическими точками функции

Для исследования критической точки на экстремум используют первое или второе достаточное условие экстремума.

Теорема 10.3 (первое достаточное условие экстремума).

Пусть функция непрерывна в окрестности критической точкии дифференцируема в выколотой окрестности точки. Если производнаяпри переходе (слева направо) через точкуменяет знак с плюса на минус, тоесть точка максимума; если с минуса на плюс, тоточка минимума.

Теорема 10.4 (второе достаточное условие экстремума).

Пусть 1) 2).

Тогда, если нечетное, то в точкеэкстремума нет;

если четное, то− точка экстремума, причем,

точка максимума при , точка минимума при.

Следствие. Пусть .

Если , то− точка максимума для;

если , то− точка минимума для.

10.3. Наибольшее и наименьшее значение функции на отрезке

На практике часто встречаются задачи, в которых требуется найти наибольшее или наименьшее значение функции на отрезке. Напомним, что функция, непрерывная на отрезке, принимает на этом отрезке наибольшее и наименьшее значения. Эти значения она принимает либо в критических точках внутри отрезка, либо на концах отрезка. Поэтому для отыскания наибольшего и наименьшего значения непрерывной на отрезке функцииследует:

1) найти критические точки функции на интервале ,

2) вычислить значения функции в этих критических точках (не исследуя их) и на концах отрезка,

3) из всех полученных значений функции выбрать наибольшее и наименьшее.