
- •Задачи оптимизации
- •Метод градиентного спуска
- •Алгоритм
- •Метод квадратичной интерполяции-экстраполяции
- •Алгоритм
- •Интерполяционные формулы Ньютона
- •Первая интерполяционная формула Ньютона
- •Вторая интерполяционная формула Ньютона
- •Решение обыкновенных дифференциальных уравнений. Многошаговые методы
- •Суть многошаговых методов
- •Метод Адамса (четырехшаговый)
- •Методы прогноза и коррекции
- •XI-3 XI-2 XI-1 XI
- •Интерполяция сплайнами
- •Контрольные вопросы
- •620002, Екатеринбург, ул. Мира, 19

В.А. Чернышев
Методические
указания для практических занятий и
самостоятельной работы
Подготовлено
кафедрой
компьютерной
физики
Рассматриваются
методы нахождения минимума (максимума)
функции, интерполяционные полиномы
Ньютона, интерполяция кубическими
сплайнами, решение ОДУ методами Адамса
Екатеринбург
2011

Оглавление
Оглавление 2
Задачи оптимизации 3
Метод градиентного спуска 3
Алгоритм 3
Алгоритм 3
Метод квадратичной интерполяции-экстраполяции 4
Алгоритм 5
Алгоритм 5
Интерполяционные формулы Ньютона 7
Первая интерполяционная формула Ньютона 9
Вторая интерполяционная формула Ньютона 11
Решение обыкновенных дифференциальных уравнений. Многошаговые методы 13
Суть многошаговых методов 14
Метод Адамса (четырехшаговый) 15
Методы прогноза и коррекции 17
Интерполяция сплайнами 21
Контрольные вопросы 27
Задачи оптимизации
Задачи оптимизации сводятся к записи целевой функции y =f (x) и отыскания еe минимума или максимума.yможет быть функцией нескольких переменных,x = (x1,x2,…,xn), тогда мы имеем многомерную задачу оптимизации. Еслиy =f (x) не задана аналитически, задачу приходится решать численно.
Метод градиентного спуска
Пусть функция fзависит от трех переменныхf =f (x,y,z).
Еe частные производные –![]() .
Градиент функции
.
Градиент функции
![]() .
.
Вектор градиента дает представление о поведении функции fвблизи точки (x,y,z). Направление этого вектора – направление наиболее быстрого возрастания функции.
Модуль градиента
![]()
определяет скорость возрастания функции в направлении градиента (или убывания в направлении антиградиента). Будем двигаться к минимуму функции в направлении наиболее быстрого убывания (антиградиента).
Алгоритм
1. Возьмем начальную
точку
![]()
2. Вычислим градиент
![]() в
этой точке.
в
этой точке.
3. Сделаем шаг в
антиградиентном направлении, т.е. найдем
точку
![]() :
:
![]()
(здесь k – численный коэффициент).
Затем берем
![]() в
качестве
в
качестве![]() и
находим следующую точку. Повторяя этот
процесс, мы приближаемся к минимуму. В
начале пути, когда
и
находим следующую точку. Повторяя этот
процесс, мы приближаемся к минимуму. В
начале пути, когда![]() большой, мы делаем шаг на малую долю
антиградиента (т.к. он меняется от точки
к точке), т.е. в начале итерацийk«1.
По мере приближения к минимуму
большой, мы делаем шаг на малую долю
антиградиента (т.к. он меняется от точки
к точке), т.е. в начале итерацийk«1.
По мере приближения к минимуму![]() уменьшается, поэтому коэффициентkцелесообразно увеличивать, вплоть доk = 1 вблизи минимума. Итерации
прекращаются, когда модуль градиента
становится достаточно малым:
уменьшается, поэтому коэффициентkцелесообразно увеличивать, вплоть доk = 1 вблизи минимума. Итерации
прекращаются, когда модуль градиента
становится достаточно малым:
![]() .
.
Заметим, что строгое
равенство
![]() в общем случае достигнуто не будет,
поскольку существует погрешность при
численном нахождении производных
в общем случае достигнуто не будет,
поскольку существует погрешность при
численном нахождении производных![]() ,
а также потому, что градиент меняется
непрерывно.
,
а также потому, что градиент меняется
непрерывно.
Метод квадратичной интерполяции-экстраполяции
Метод квадратичной интерполяции-экстраполяции, или, как его еще называют, «метод парабол», основан на замене функции параболой. Вместо минимума функции находится минимум параболы.

Рис. 1
Рассмотрим сначала одномерный случай. Вычислим три значения функции y (x) в точкахx0,x1,x2, причем, возьмем эти точки равноотстоящими.
Интерполируем функцию y(x) полиномом Лагранжа:
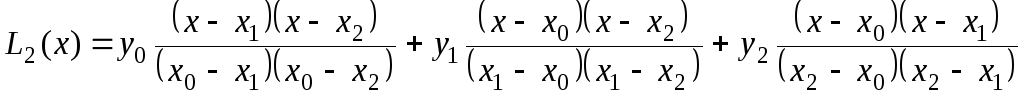 .
.
Учтем, что x0,x1,x2равноотстоящие (см. рис. 1), тогда
![]() .
.
Найдем экстремум полинома:
![]() ,
,
![]() ,
,
отсюда
![]() .
.
Обозначим
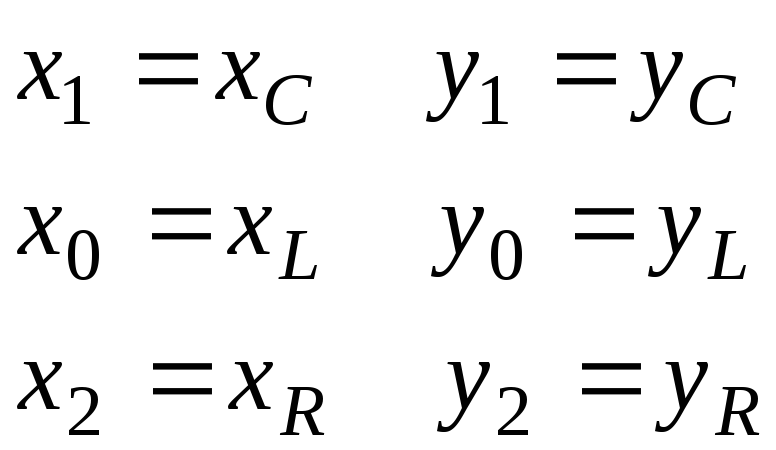
тогда
![]() (*)
(*)
Таким образом, мы нашли экстремум параболы, проходящей через три точки функции f (x).
Алгоритм
Задаются величины h(шаг) и ε (точность), причем ε <h. Например,
ε = 0,001, h= 0,01.
Берeтся стартовая
точка
![]() ,
из каких-либо соображений близкая к
экстремуму. Полагается
,
из каких-либо соображений близкая к
экстремуму. Полагается![]() ,
,
вычисляются
![]()
затем
![]() .
.
По формуле (*)
находится
![]() .
Если
.
Если![]() ,
берут
,
берут![]() и повторяют процесс. Итерации прекращают,
когда
и повторяют процесс. Итерации прекращают,
когда![]() .
Точка
.
Точка![]() является приближением экстремума
функцииf (x) с
точностью ε.
является приближением экстремума
функцииf (x) с
точностью ε.
Заметим, что шаг
и точность часто берут в долях стартового
значения, например,
![]() ,
чтобы они соответствовали диапазону,
в котором меняется переменнаяx.
,
чтобы они соответствовали диапазону,
в котором меняется переменнаяx.
Многомерный случай
Если
![]() .
.
Задаются величины
![]()
т.е. по каждой переменной свой шаг и своя точность.
Берем стартовую
точку
![]() .
.
Сводим задачу к одномерной.
Фиксируем переменные
![]() .
Берем
.
Берем![]() ,
,![]() ,
,![]() затем
вычисляем
затем
вычисляем![]() .
(При этом функция
.
(При этом функция![]() является
функцией одной переменной, т.к. все
переменные кроме одной- фиксированы).
Вычисляем
является
функцией одной переменной, т.к. все
переменные кроме одной- фиксированы).
Вычисляем![]() по
формуле (*). Чтобы найти
по
формуле (*). Чтобы найти![]() фиксируем
переменные
фиксируем
переменные![]() .
.
Находим![]() ,
,![]() ,
,![]() .
Вычисляем
.
Вычисляем![]() ,
затем
,
затем![]() по
формуле (*).
по
формуле (*).
Таким образом,
поочередно фиксируя все переменные,
кроме i-ой, найдем![]() -е
и получим новый вектор
-е
и получим новый вектор
![]() .
.
Если хотя бы для одной его компоненты будет выполняться
![]() ,
,
то берем
![]() и повторяем процесс. Итерации останавливают,
когда для всехi
выполняется
и повторяем процесс. Итерации останавливают,
когда для всехi
выполняется
![]() .
.
Отметим, что метод парабол находит экстремум функции, т.е. минимум или максимум, в зависимости от текущего рельефа. В отличие от метода градиентного спуска, который находит именно минимум.
