Решение обыкновенных дифференциальных уравнений. Многошаговые методы

Вспомним задачу Коши:

Необходимо найти функцию , такую, что

и

.

В случае, когда задача решается численно, в точках , отстоящих друг от друга на расстояние , находятся числа – которые являются приближением точного решения

.

Значение , в общем случае, находится как

.

Вид выражения Fзависит от конкретного численного метода. Например, в методе Эйлера – Коши:

,

а здесь находится по методу Эйлера:

.

Общее выражение для метода Эйлера – Коши:

– здесь в правой части равенства есть .

Общее выражение для метода Эйлера:

– в правой части равенства -го нет.

Методы, в правой части которых отсутствует , называютсяявными(т.е. вычисляется явно, по предыдущему значению ). Если в правой части равенства присутствует , то метод называетсянеявным. Таким образом, метод Эйлера – явный, а Эйлера – Коши – неявный.

Суть многошаговых методов

В этих методах для вычисления -го значения используется не одно значение , а несколько предыдущих значений:

– kпредыдущих значений. Т.е. используются результатыkпредыдущих шагов, поэтому – «многошаговые методы».

Вернемся к задаче Коши. Равенство

проинтегрируем на отрезке :

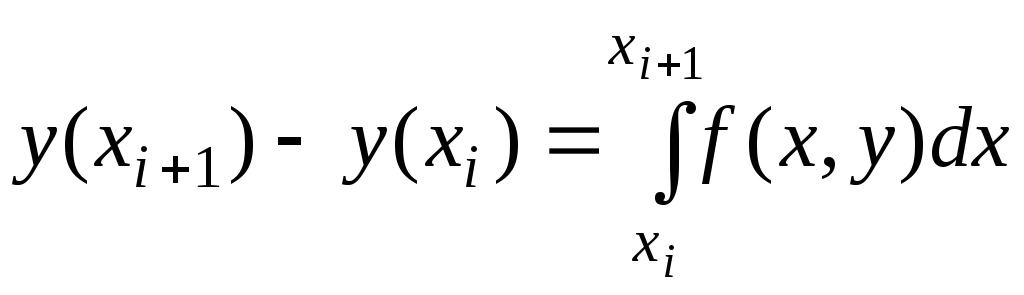
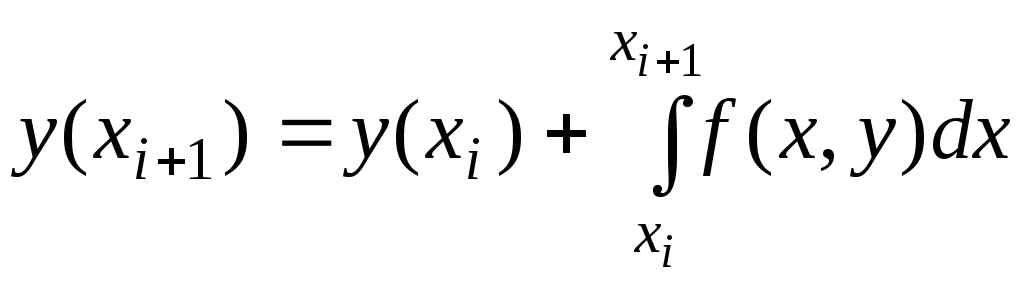
Для приближенного вычисления интеграла в правой части равенства заменим подынтегральную функцию полиномом , который построим поk точкам . После такой интерполяции

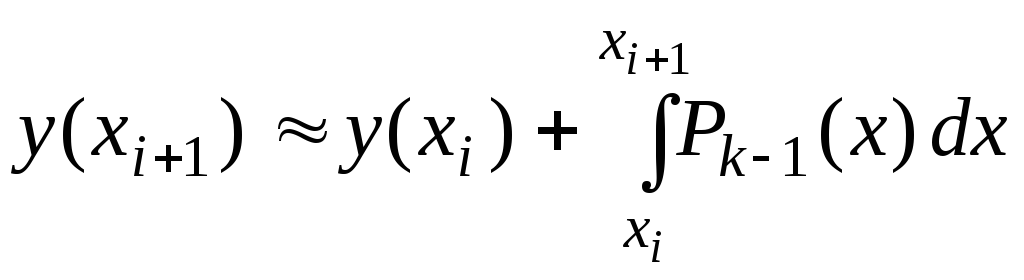
и формула для расчета приближенного значения -го в точке будет

.

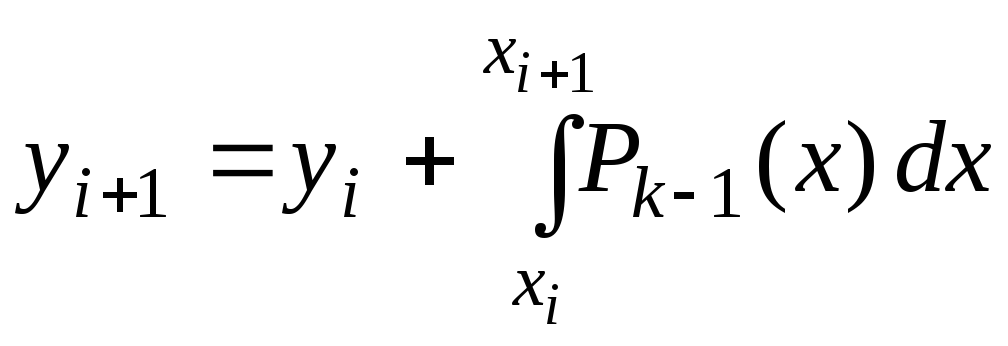На основе этой общей формулы стоятся многошаговые методы. Порядок точности многошагового метода зависит от степени интерполяционного многочлена для построения которого используются значения , вычисленные на предыдущихkшагах.

Семейством многошаговых методов являются методы Адамса. Простейший из них, получающийся при k = 1, совпадает с методом Эйлера:

.

т.е. на отрезке функцию заменяем (интерполируем) константой, равной , значению функцииfв точке :

.

На практике чаще всего применяется метод Адамса, использующий на каждом шаге результаты предыдущих четырех шагов, k = 4, четырехшаговый метод, имеющий четвертый порядок точности.

Метод Адамса (четырехшаговый)

Пусть найдены значения в четырех точках (k = 4) и вычислены значения , где . Чтобы построить интерполяционный многочлен , воспользуемся второй интерполяционной формулой Ньютона «назад». Для этого рассчитаем конечные разности:

Полином Ньютона для интерполирования «назад» имеет вид:

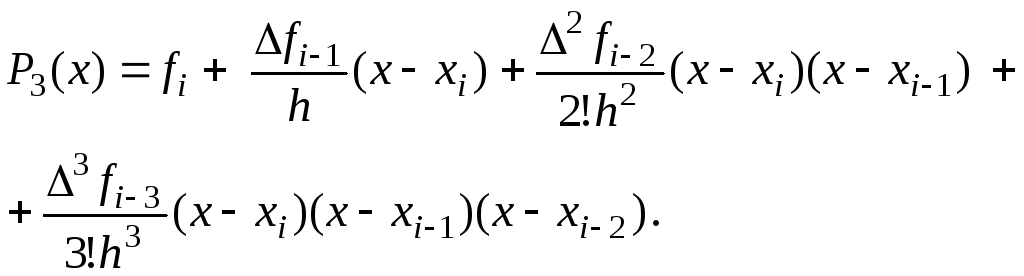
Шаг hмы здесь предположили постоянным. Введем переменную:

.

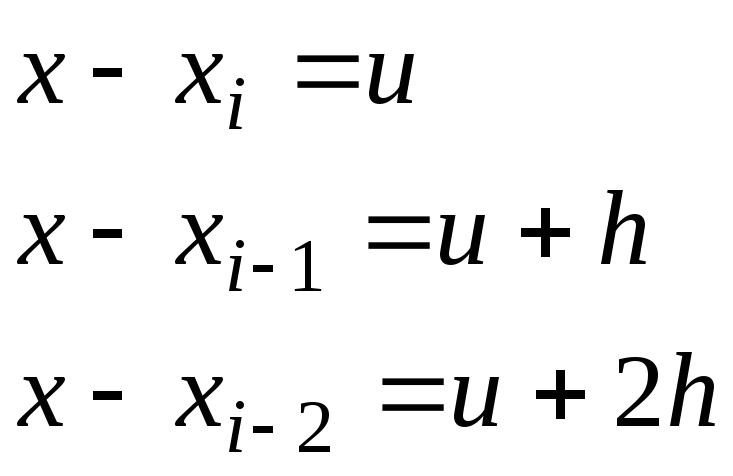
Полином необходимо проинтегрировать. Отрезок интегрирования для переменной xесть. Переменнаяuравна, поэтому отрезок интегрирования для неe.

При интегрировании полинома по uпридется интегрировать выражения:

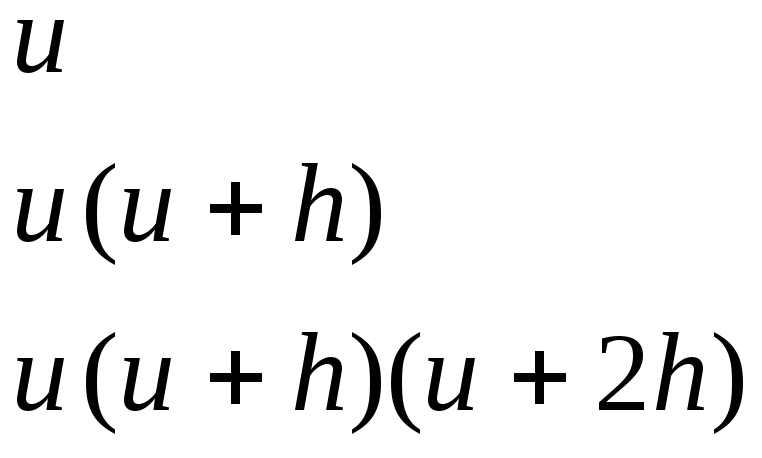
Раскрыв скобки, получим:

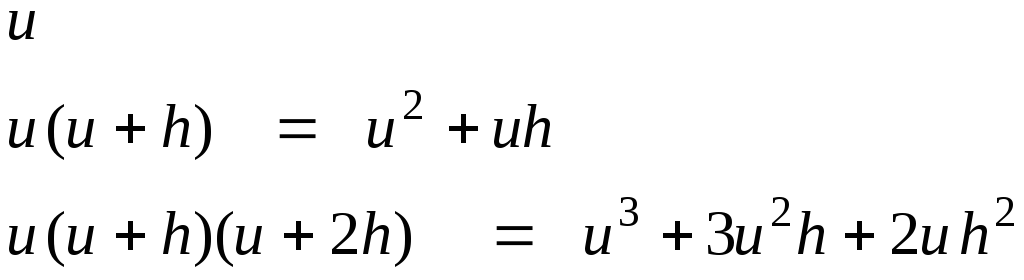
Интегрирование этих выражений сведется к вычислению интегралов:

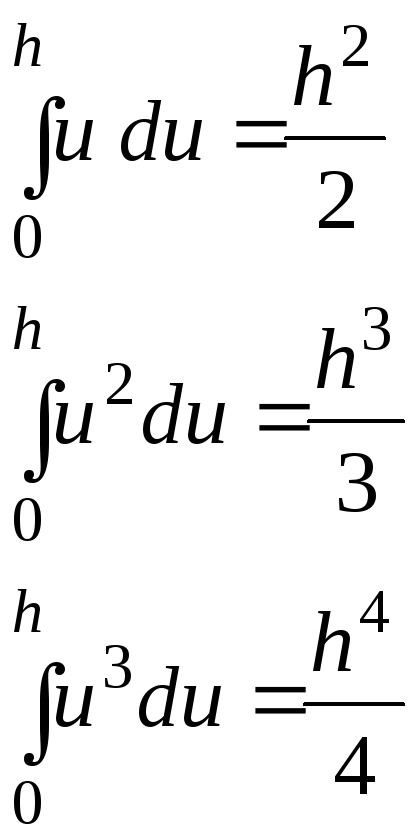
В результате, интегрирование полинома даст:

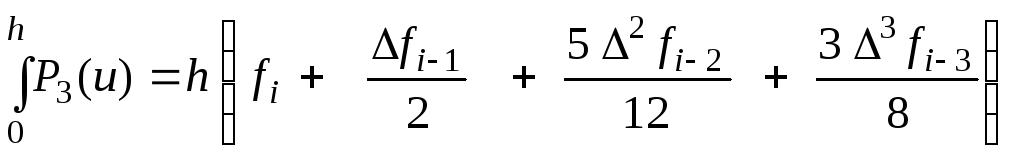
Итак,

.

Для того, чтобы этой формулой воспользоваться, необходимо вычислить конечные разности

по значениям функции . А для этого, в общем случае, необходимо знать значенияyв этих точках. Конечные разности вычислять легко, но метод Адамса неудобен тем, что нельзя начать счет только по одному значению. Значения и необходимо найти. Значения обычно находятся методом Рунге – Кутта 4-го порядка, поскольку они должны быть найдены с точностью, которая не меньше той, что у метода Адамса.

Запишем формулу метода Адамса через , без конечных разностей:

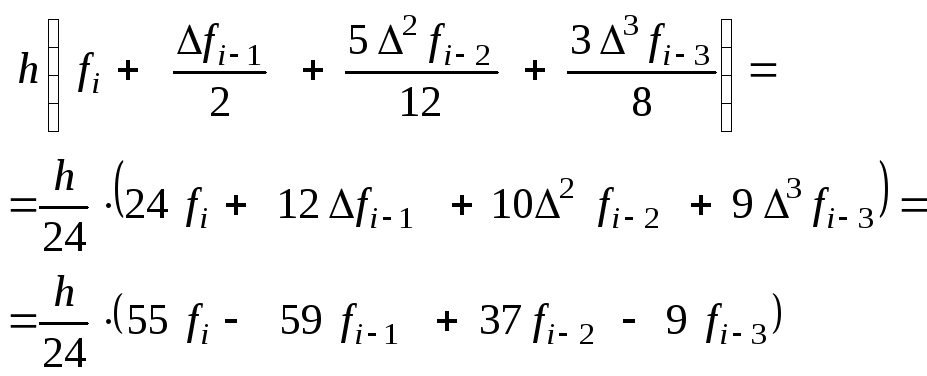
т.е.

– формула Адамса.

После того, как найдены точки необходимые для старта, т.е. на всех последующих шагах, кроме первого – метод Адамса экономичен: для совершения шага необходимо вычислить только один раз – остальные три значения используются с предыдущего шага (естественно, их номера при этом изменятся – станет и т.д. ). Т.е. метод Адамса обеспечивает четвертый порядок точности при одном вычислении на шаге , тогда как метод Рунге – Кутта, например, при такой же точности, требует четырех вычислений . Поэтому целесообразно использовать его только для нахождения стартовых точек, необходимых для «запуска» метода Адамса, а дальше двигаться методом Адамса с меньшими затратами.