
ПП_21_Опр_инт_1
.docПП 21. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ.
Методы ИНТЕГРИРОВАНИя
Определение
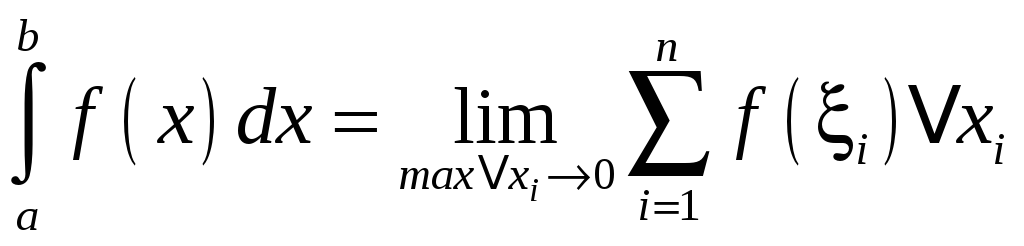 ,
,
где
![]() непрерывная функция.
непрерывная функция.
Г еометрически
определённый интеграл
еометрически
определённый интеграл
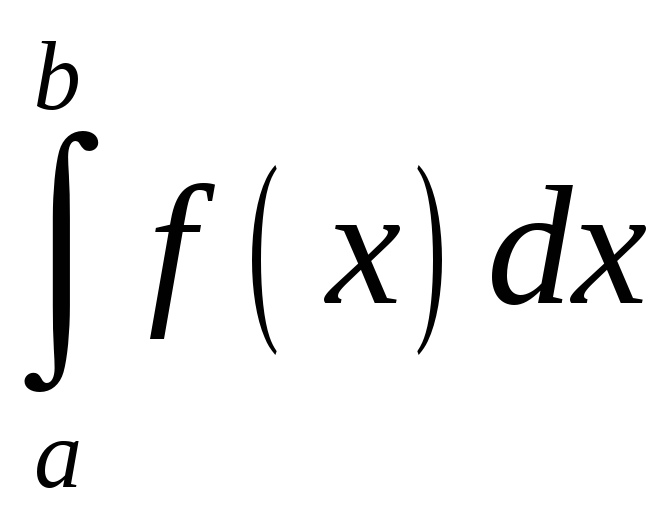 представляет собой алгебраическую
сумму площадей фигур, ограниченных
графиком функции
у
=f(х),
осью ох
и прямыми х
=
а и х
= b,
причем площади, расположенные выше оси
Ох,
входят со знаком плюс, а площади,
расположенные ниже оси Ох,
- со знаком минус.
представляет собой алгебраическую
сумму площадей фигур, ограниченных
графиком функции
у
=f(х),
осью ох
и прямыми х
=
а и х
= b,
причем площади, расположенные выше оси
Ох,
входят со знаком плюс, а площади,
расположенные ниже оси Ох,
- со знаком минус.
Свойства определенного интеграла
1.
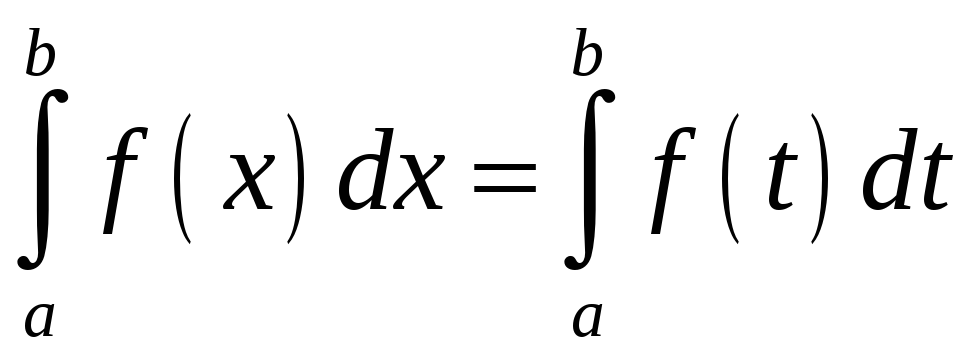 .
.
2.
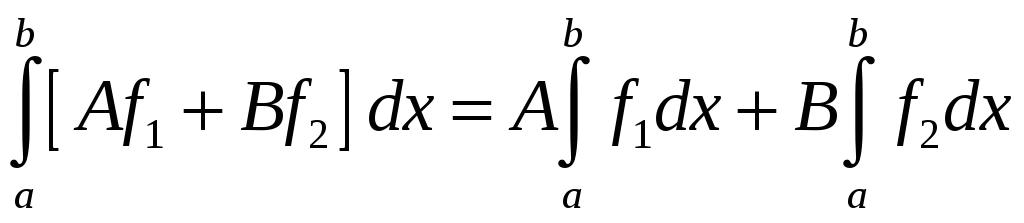 ,
А, В - постоянные.
,
А, В - постоянные.
3.
 ,
,
для
любых трех чисел
![]() ,
,
![]() ,
,
![]() .
.
4. Если
1)
![]() интегрируема на
интегрируема на
![]() ;
2)
;
2)
![]() для любых
для любых
![]() ,
,
тогда
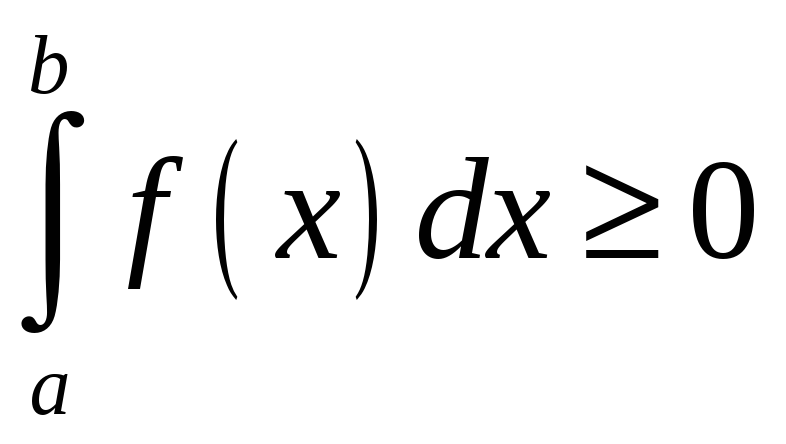 .
.
5. Если
1)
![]() ,
,
![]() интегрируемы на
интегрируемы на
![]() ;
2)
;
2)
![]() для любых
для любых
![]() ,
тогда:
,
тогда:
 .
.
6. Если
1)
![]() интегрируема на
интегрируема на
![]() ;
;
2)
m
и M
-наименьшее
и наибольшее значения функции
![]() ,
,
тогда
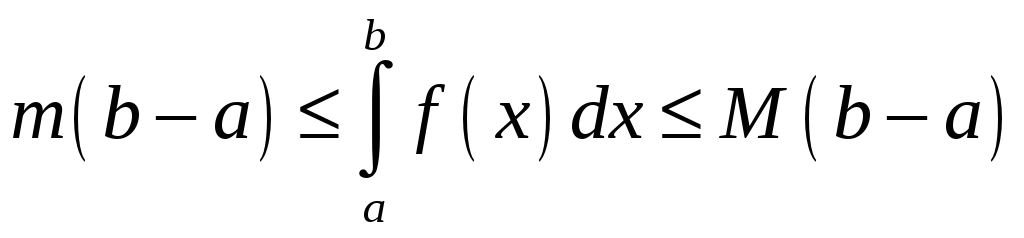 .
.
7.
Если
![]() непрерывна на
непрерывна на
![]() ,
,
то
![]() такая, что
такая, что
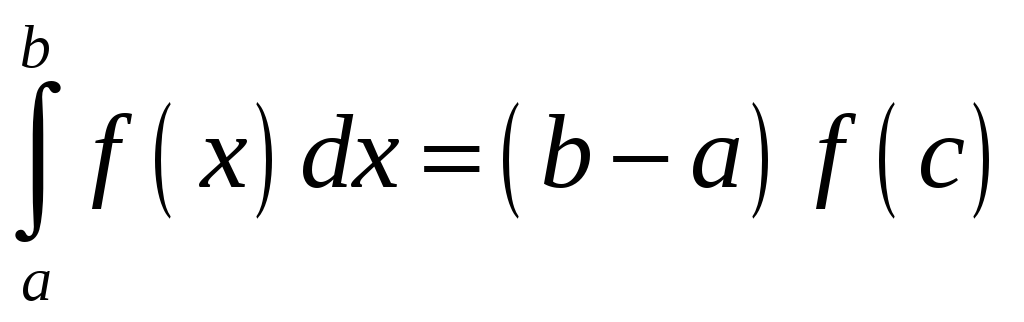 .
.
Число
 называется средним
значением
функции
называется средним
значением
функции
![]() на отрезке
на отрезке
![]() .
.
8.
Если
![]() непрерывна на
непрерывна на
![]()
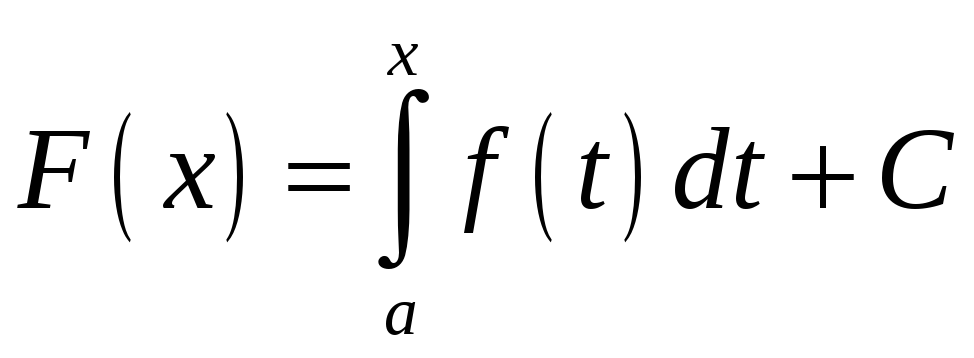 ,
,
![]() .
.
9.
Производная от интеграла по переменному
верхнему пределу равна
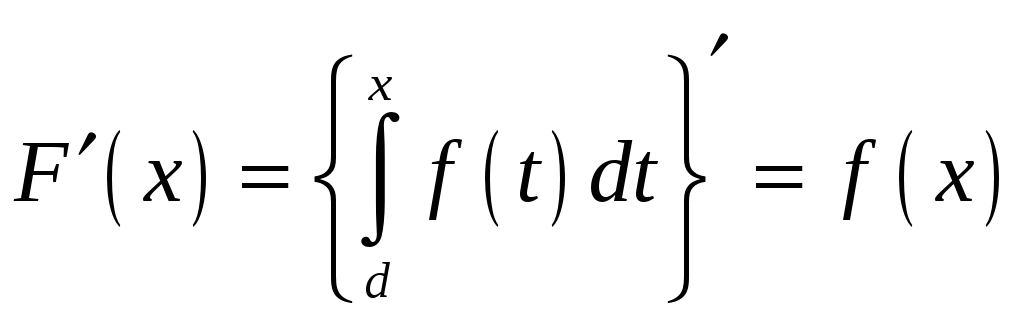
10.
Если функции
![]() и
и
![]() дифференцируемы в точке х
дифференцируемы в точке х
![]() и
и
![]() непрерывна при
непрерывна при
![]() ,
то
,
то
 .
.
11.
 - формула Ньютона-Лейбница.
- формула Ньютона-Лейбница.
Для
вычисления определенного интеграла от
непрерывной функции
![]() нужно:
нужно:
1) не
обращая внимания на пределы интегрирования
найти первообразную
![]() для подынтегральной функции (по правилам
вычисления неопределенного интеграла);
для подынтегральной функции (по правилам
вычисления неопределенного интеграла);
2) вычислить
![]() .
.
12. Если
1)
![]() непрерывна на
непрерывна на
![]() ;
;
2)
![]() - непрерывно дифференцируема на
- непрерывно дифференцируема на
![]() (
(![]() - область значений
- область значений
![]() при изменении
при изменении
![]() );
);
3)
![]() ,
,
![]() ,
,
тогда
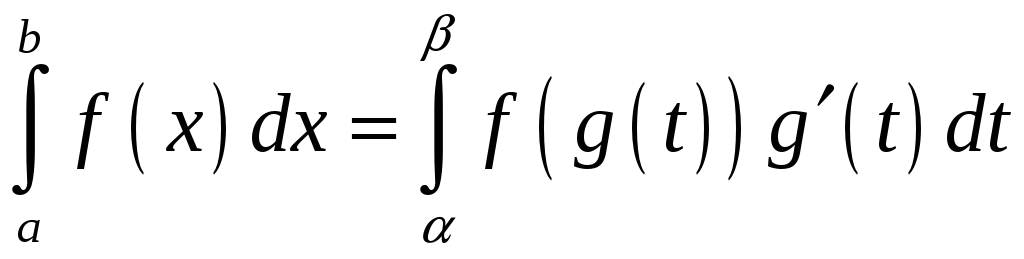
- формула замены переменной под знаком определенного интеграла.
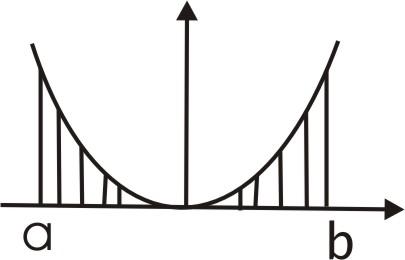
12. Если
-
1)
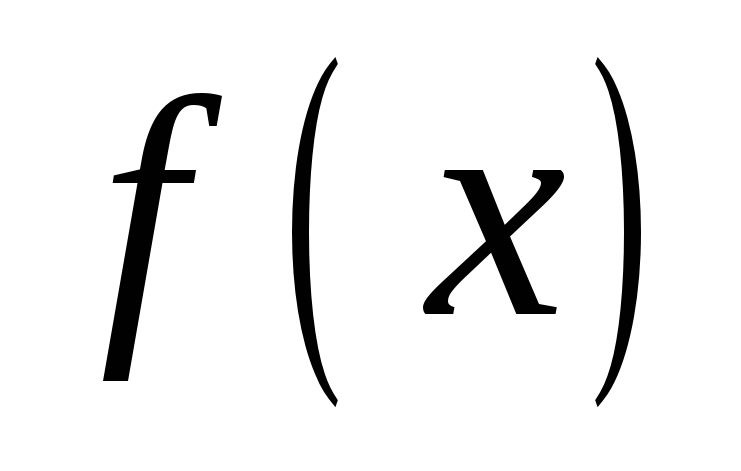 - четная
- четная
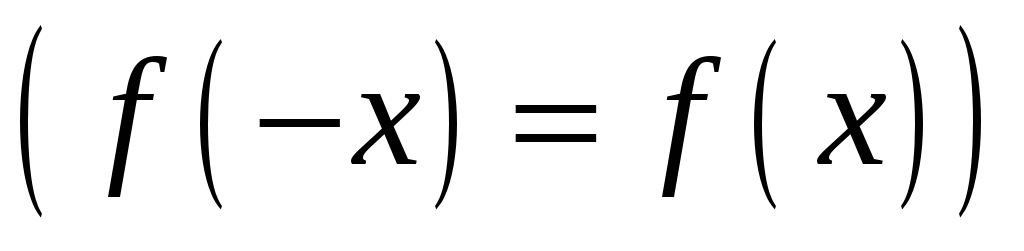 ,
,
то
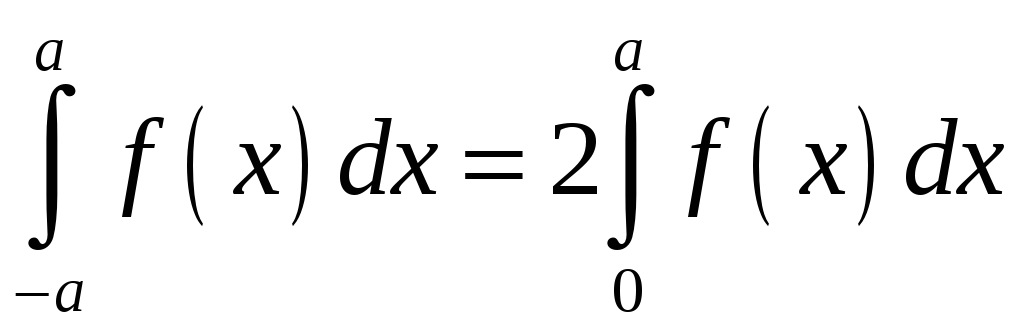
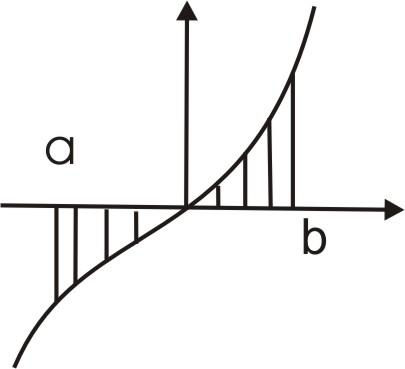
2)
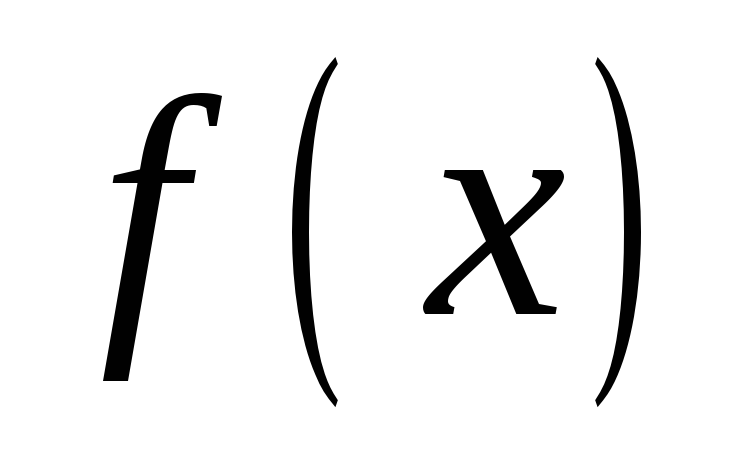 - нечетная
функция
- нечетная
функция
 ,
, .
.
13.
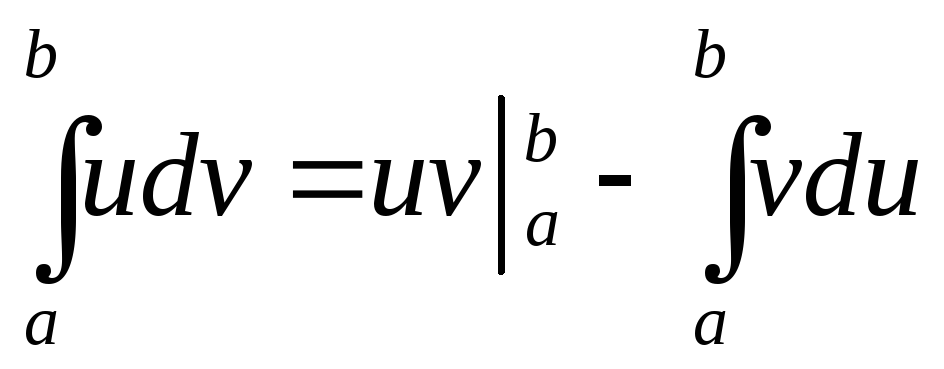 .
.
|
ПП 20. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ |
||
|
№ п/п |
Задача |
Ответ |
|
ПП 21 №1 |
Вычислите
Решение:
В
качестве
Пусть
|
|
|
ПП 21 №2 |
С помощью определенного интеграла найдите предел суммы
Решение: Рассмотрим
выражение под знаком предела как
интегральную сумму для
В
качестве
Пусть
|
1 |
|
ПП 21 №3 |
Оцените
интеграл
Решение: Для
0
х
1: 1
1 + х4
2,
т.е.
m
=
Следовательно,
|
|
||||||
|
ПП 21 №4 |
Определите
знак интеграла
Решение: Разобьём интеграл на два
{поменяем в первом интеграле пределы} =
{заменим в первом интеграле х (х)} =
на отрезке х0, 1, х3 0, ех ех 0,
следовательно,
т.о. интеграл имеет положительный знак. |
|
||||||
|
ПП 21 №5 |
Найдите производную функции
Решение:
|
|
||||||
|
ПП 21 №6 |
Найдите производную функции Ф(х)
= Решение: (х) = 0, (х) = 0, (х) = х2. Ф(х)
=
|
2х |
||||||
|
ПП 21 №7 |
Не
вычисляя интегралов, выяснить, какой
из интегралов
Решение: Сравним
подынтегральные функции на отрезке
интегрирования.
|
Второй |
||||||
|
ПП 21 №8 |
Найдите
среднее значение функции
Решение:
|
|
||||||
|
ПП 21 №9 |
Оцените
интеграл
Решение: На
отрезке
|
|
||||||
|
ПП 21 №10 |
Вычислите
Решение:
|
|
||||||
|
ПП 21 №11 |
Вычислите
Решение:
|
2 |
||||||
|
ПП 21 №12 |
Вычислите
Решение:
= ln(ln e2) ln(ln e) = ln 2 0,69. |
ln 2 0,69 |
||||||
|
ПП 21 №13 |
Вычислите
Решение:
|
1
|
||||||
|
ПП 21 №14 |
Вычислите
Решение:
|
|
||||||
|
ПП 21 №15 |
Вычислите
Решение:
=
|
|
||||||
|
ПП 21 №16 |
Вычислите.
Решение:
|
|
||||||
|
ПП 21 №17 |
Вычислите
РЕШЕНИЕ:
= |
0,5 |
||||||
|
ПП 21 №18 |
Вычислите
РЕШЕНИЕ:
=
=
2(х2
+ 2)
=
=
= |
3,81 |
||||||
|
ПП 21 №19 |
Вычислите
Решение: |
|
||||||
|
ПП 21 №20 |
Вычислите
РЕШЕНИЕ.
=
=
2 arctg
|
0,04 |
||||||
|
ПП 21 №21 |
Вычислите
РЕШЕНИЕ:
|
23,1 |
||||||
|
ПП 21 №22 |
Вычислите
РЕШЕНИЕ: х(х + 4)(х 2) = х3 +2х2 8х;
=
2
4
=2х
4
Вычислим неопределенные коэффициенты А, В и С. Приведем правую часть равенства к общему знаменателю:
= откуда
х2 + 6х + 2 = А (х + 4)(х 2) + Вх (х 2) + Сх(х + 4). Приравняем коэффициенты при одинаковых степенях х:
откуда
А
=
Интеграл
4 = = = =10+ =4
+
|
1,83 |
||||||
|
ПП 21 №23 |
Вычислите
РЕШЕНИЕ:
откуда А(х + 2)3 + В(х 2)(х + 2)2 + С(х + 2)(х 2) + +D(х 2= х3 + 6х2 + 13х + 6, А
= 1, В
= С
= 0, D
= 1
=
ln1
|
0,62 |
||||||
|
ПП 21 №24 |
Вычислите
РЕШЕНИЕ: Интеграл от правильной дроби, разложим ее на простейшие
2х3 + 3х2 + 3х + 2 = (Ах + В)(х2 + 1) + (Сх + D)(х2 + х + 1), или
Отсюда
= +
=
|
1,02 |
||||||
|
ПП 21 №25 |
Вычислите
РЕШЕНИЕ: Применим
универсальную тригонометрическую
подстановку t
=
sin
x
=
При
х
=
I= =
4
t
= (5
I= |
0,14 |
||||||
|
ПП 21 №26 |
Вычислите
РЕШЕНИЕ: I
=
=
Разложим дробь на простейшие:
откуда (Аt + B)(t2 + 1) + (Ct +D)(t5 + 5) = 3t2 1,
I=
= =
|
0,25 |
||||||
|
ПП 21 №27 |
Вычислите
РЕШЕНИЕ:
= = = |
|
||||||
|
ПП 21 №28 |
Вычислите
РЕШЕНИЕ: I= =
=
Разложим дробь на простейшие:
I= = |
|
||||||
|
ПП 21 №29 |
Вычислите
РЕШЕНИЕ:
= |
0,4 |
||||||
|
ПП 21 №30 |
Вычислите
РЕШЕНИЕ:
= =
=
|
0,78 |

 ;
;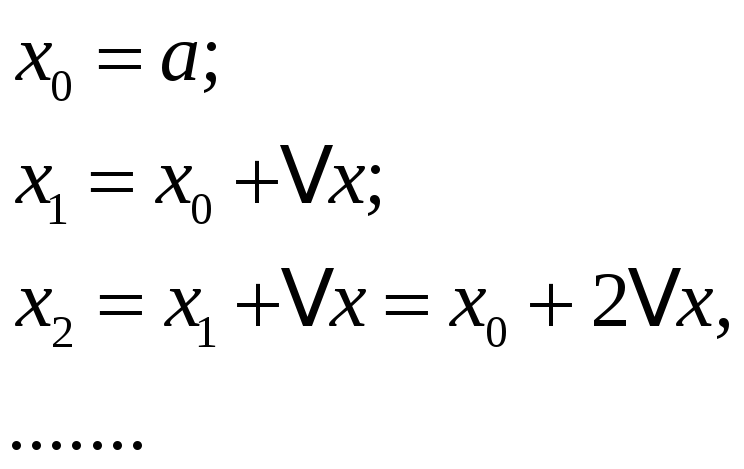
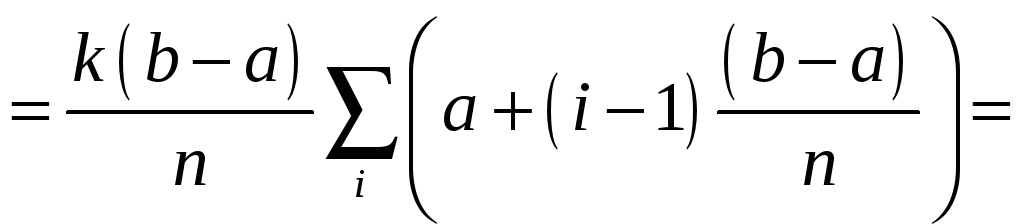
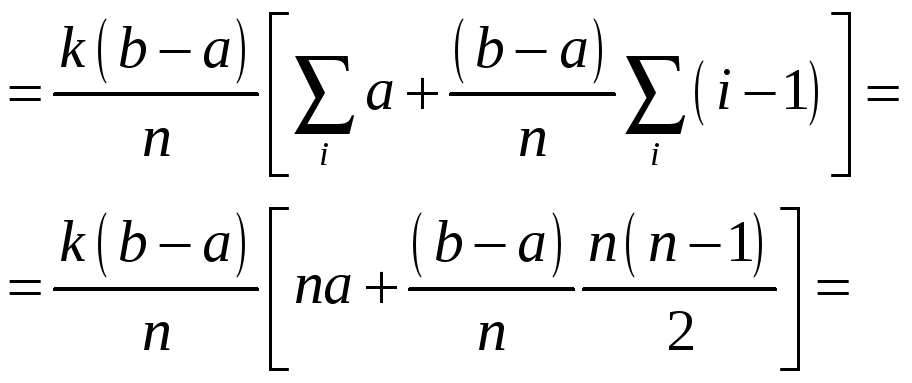
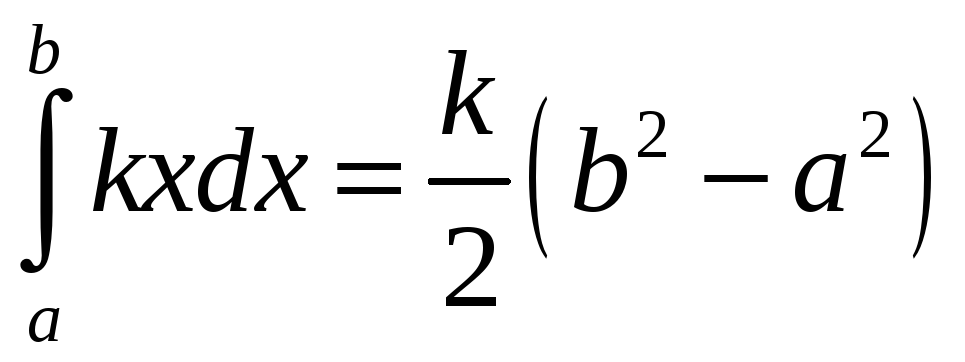
 :
:
 .
.
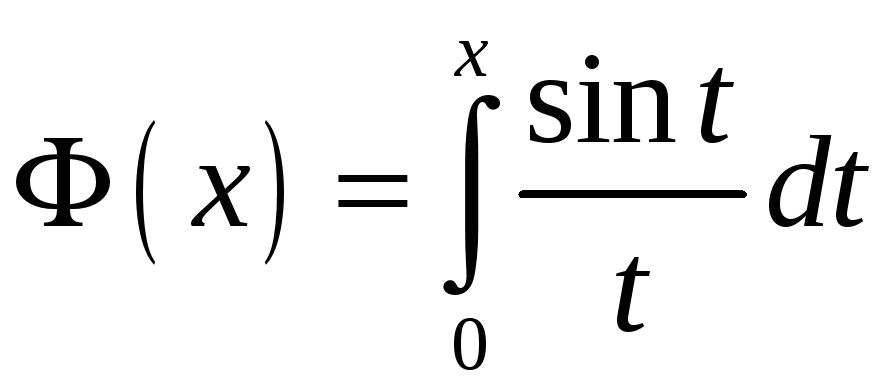
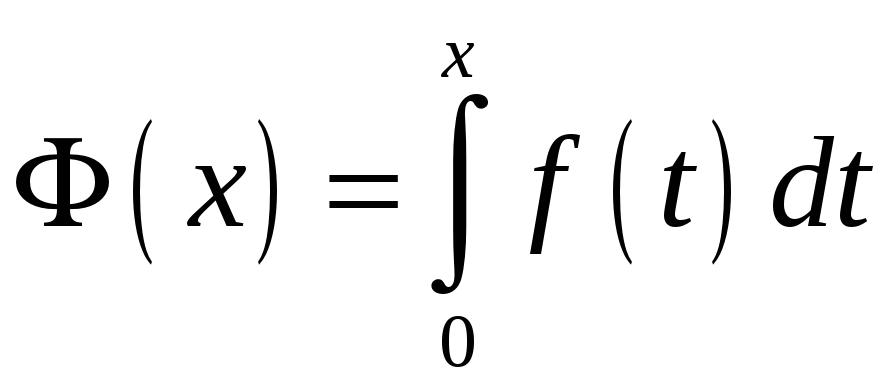
 .
.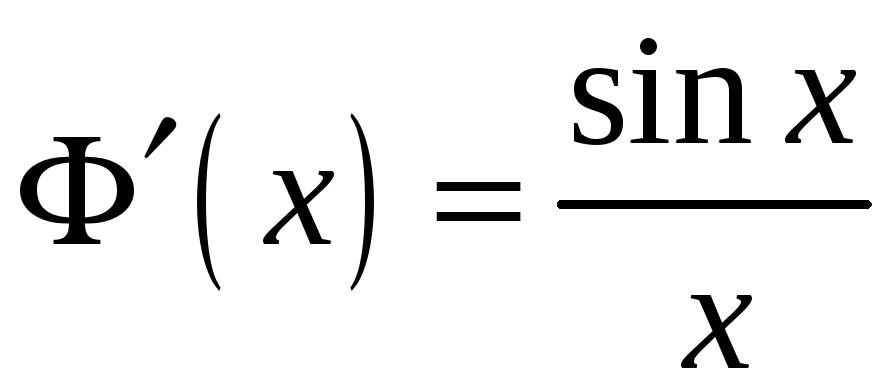
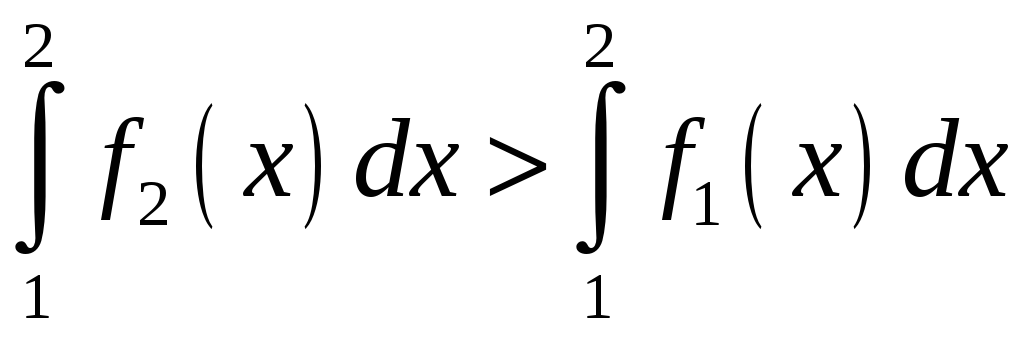 .
. .
.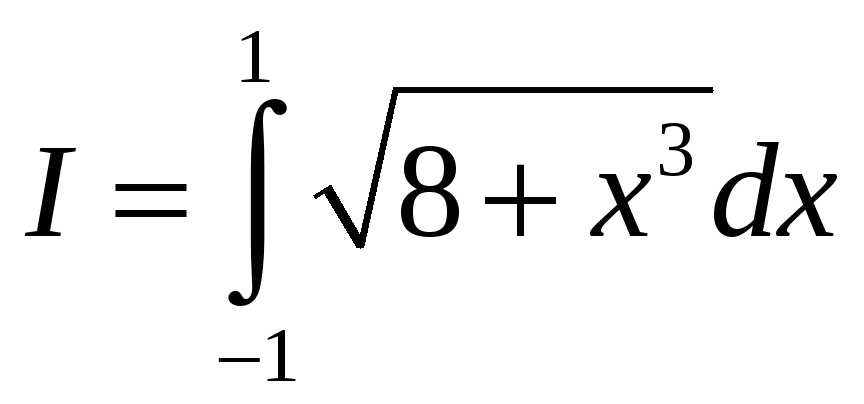
 .
.
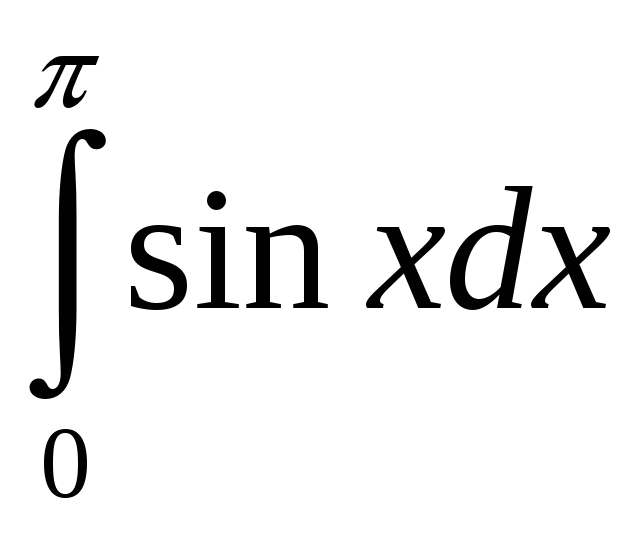 .
.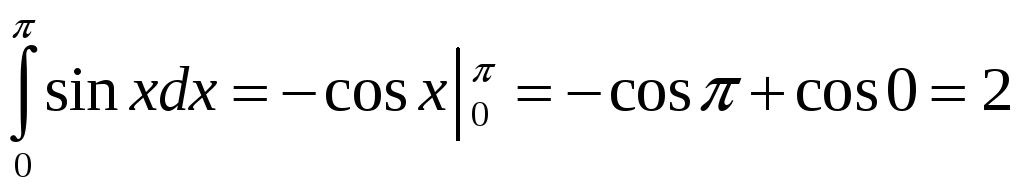
 .
.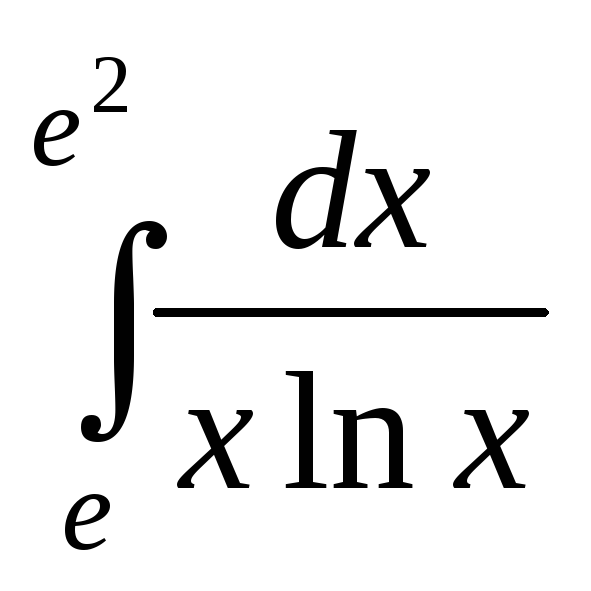 =
=
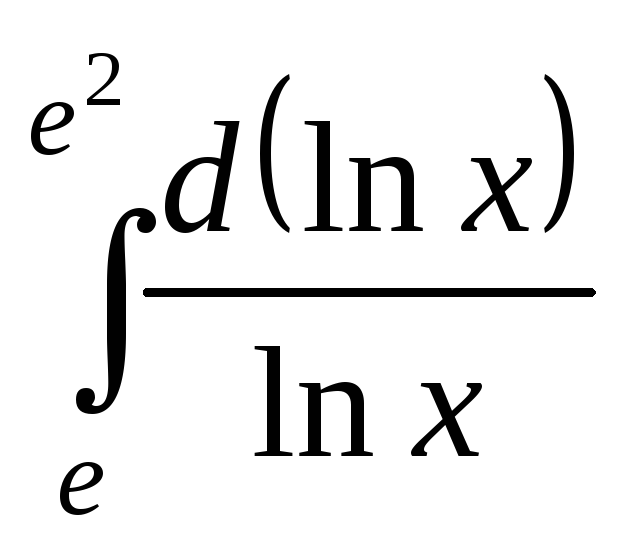 =
= .
.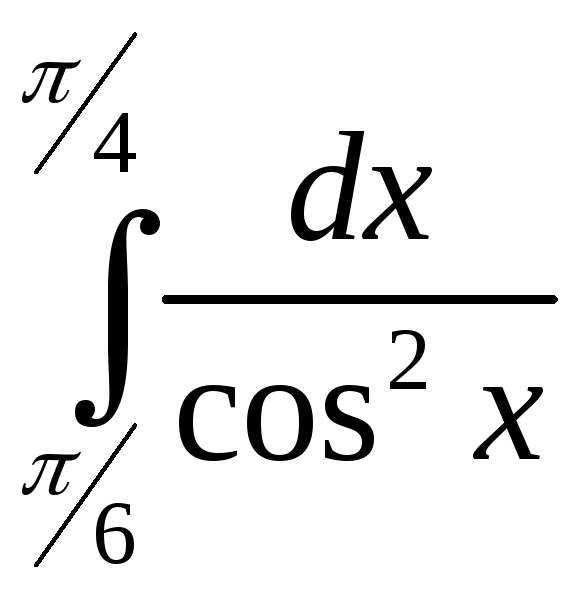 =
=
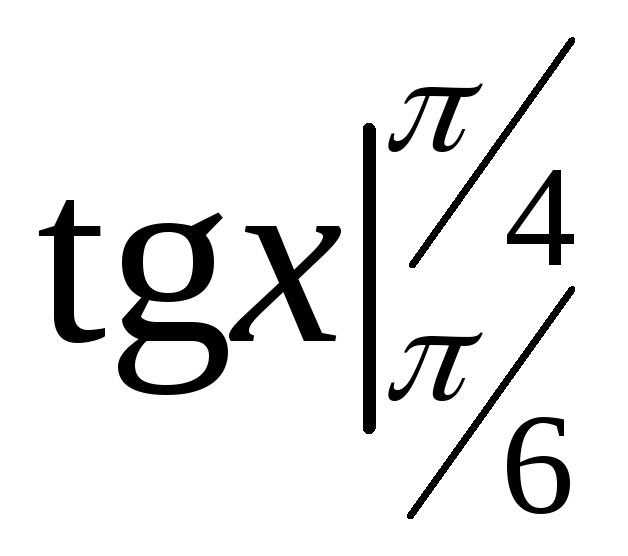 =
=
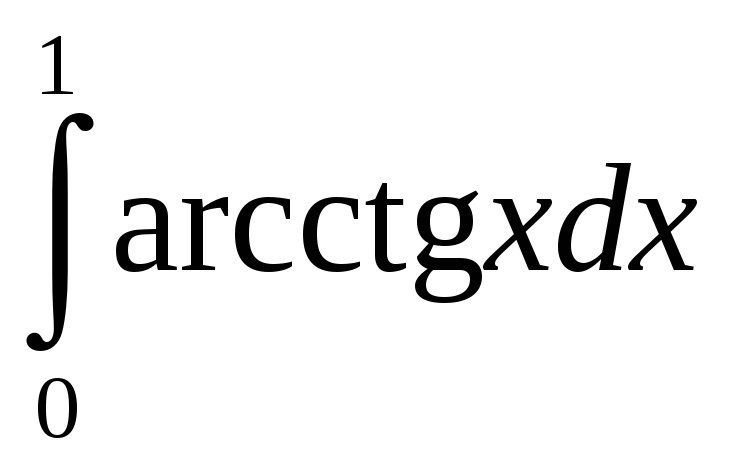 .
.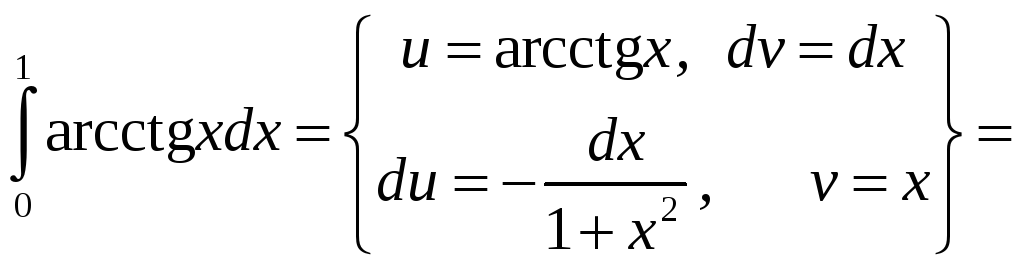


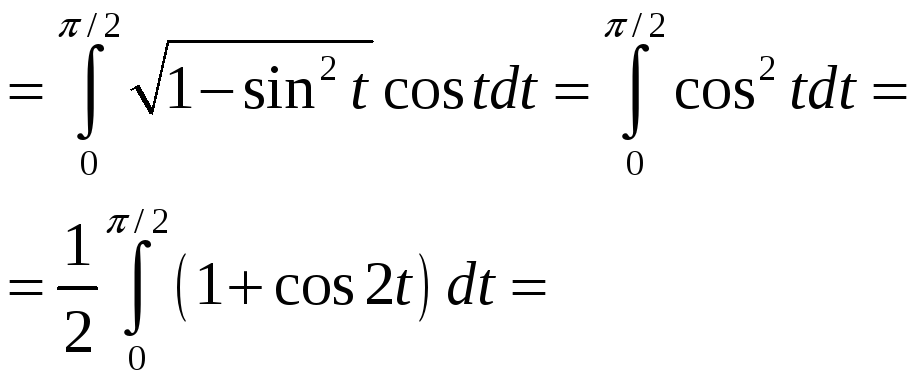
 .
.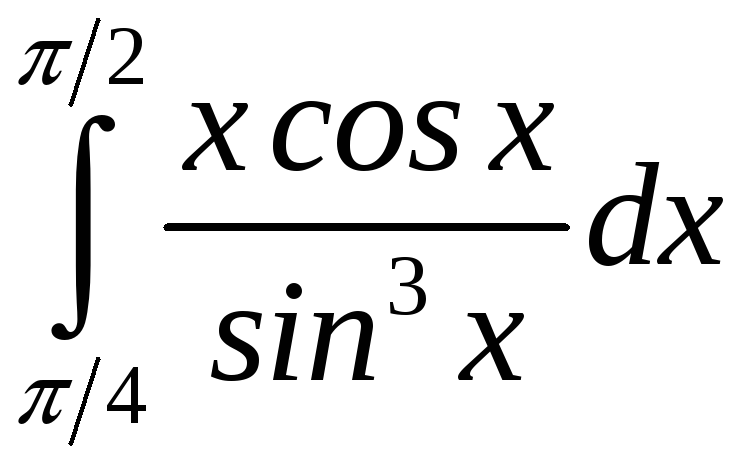 .
.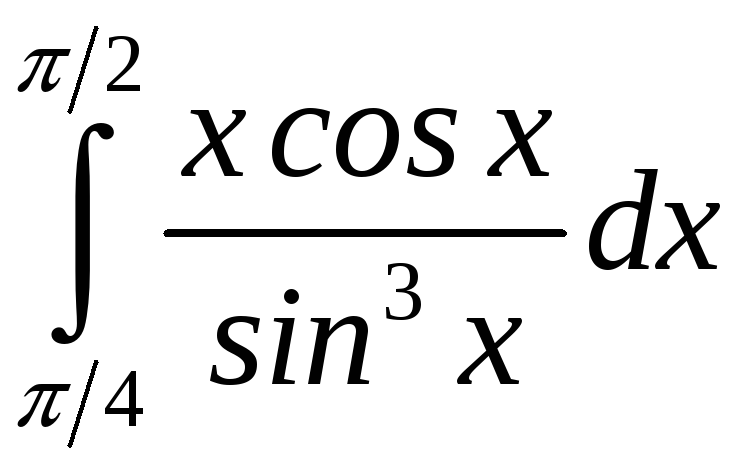 =
=
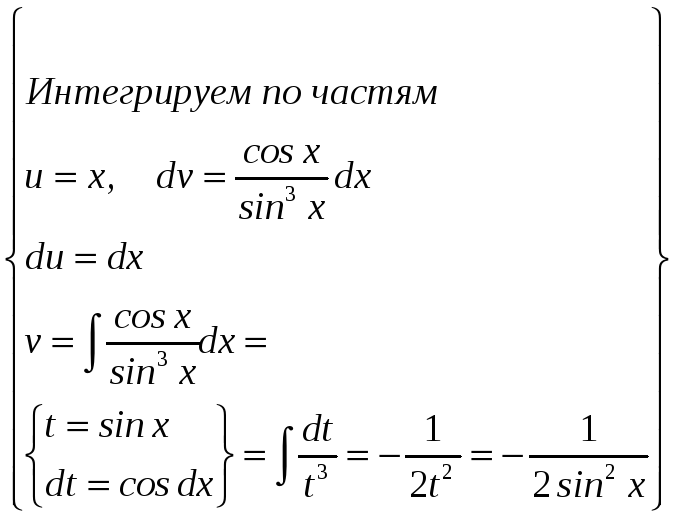
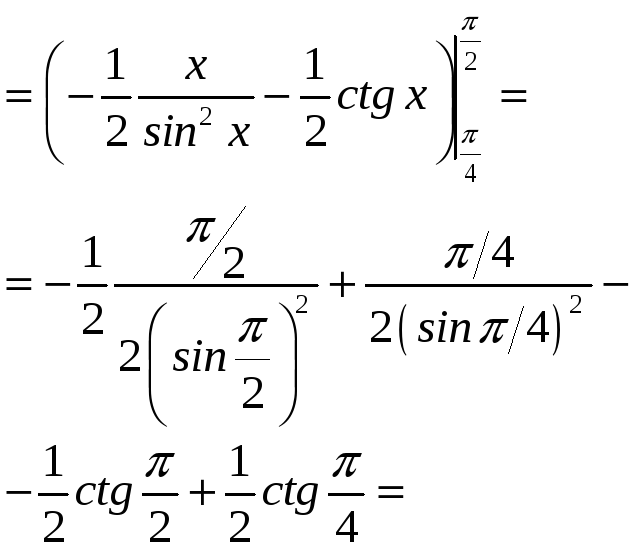
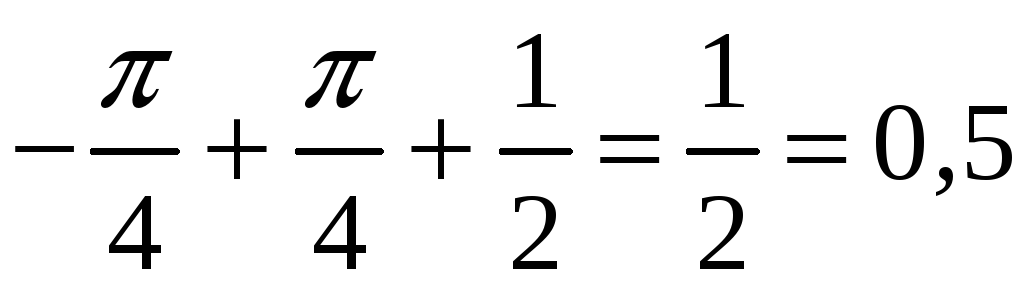 .
.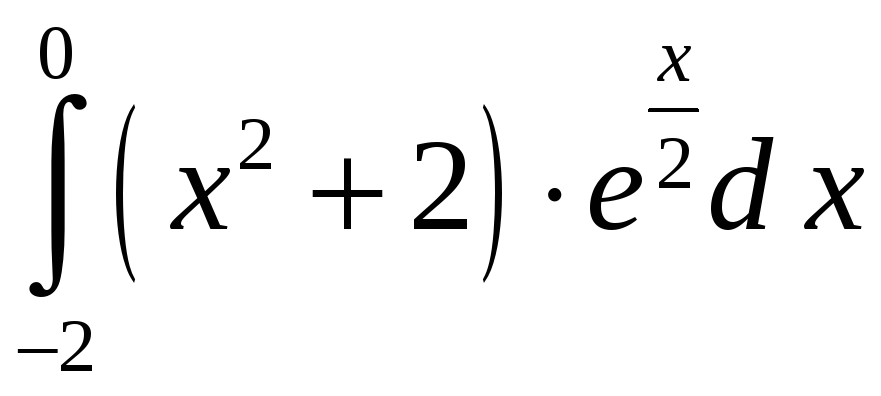 .
.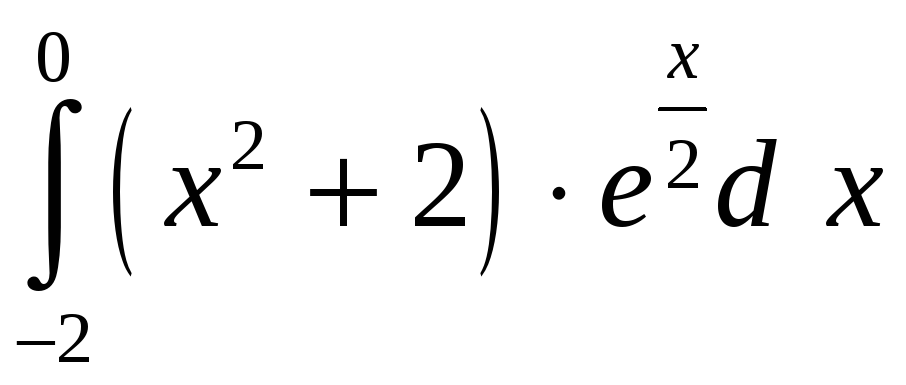 =
=
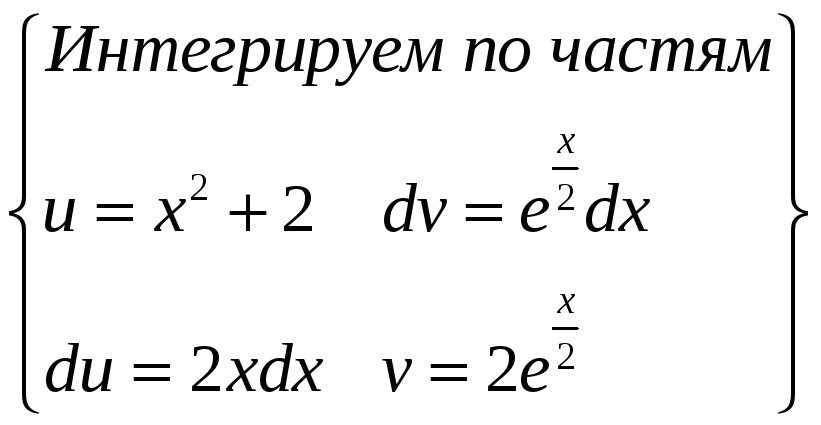
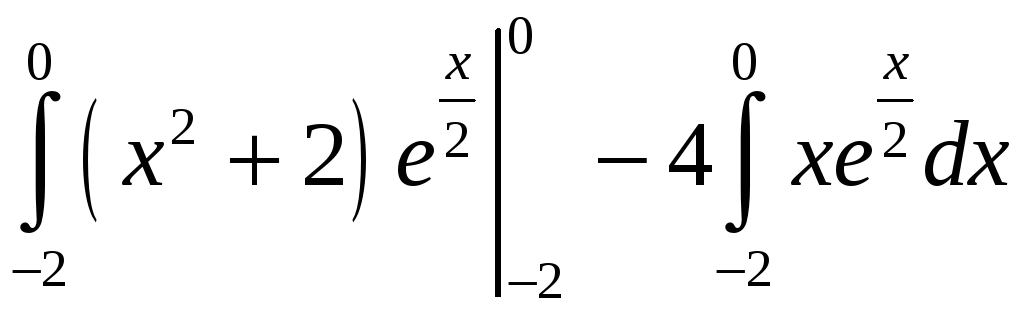 =
=

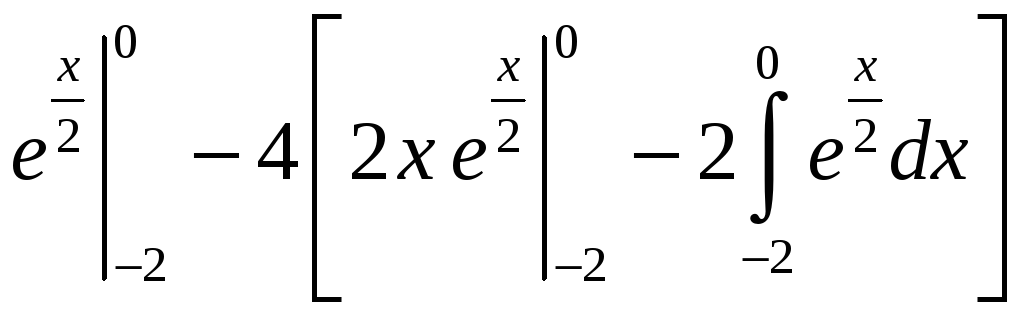 =
=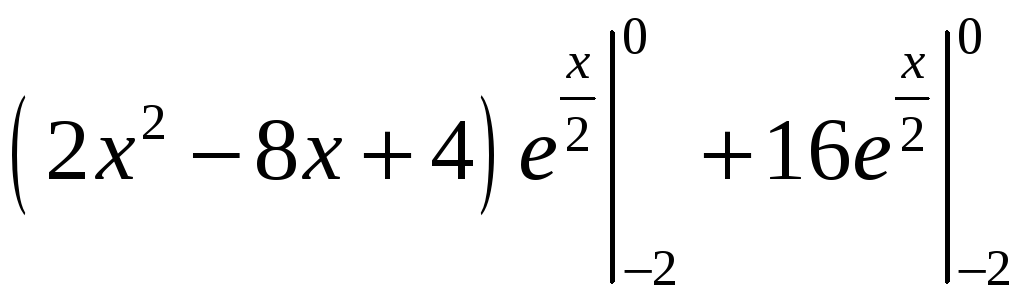 =
= =
=
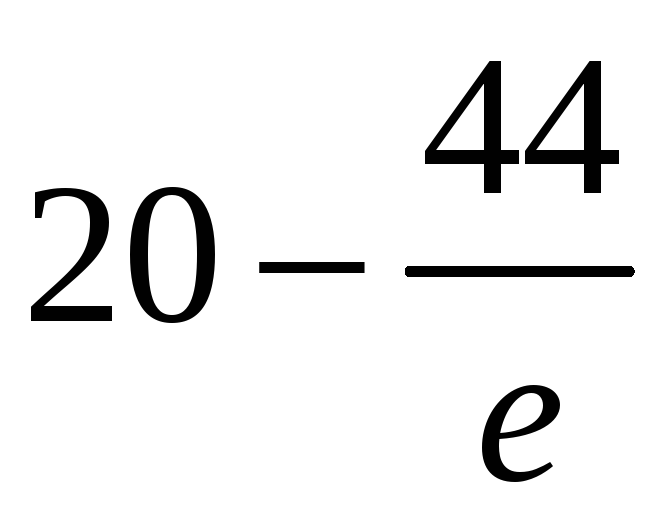
3.81
3.81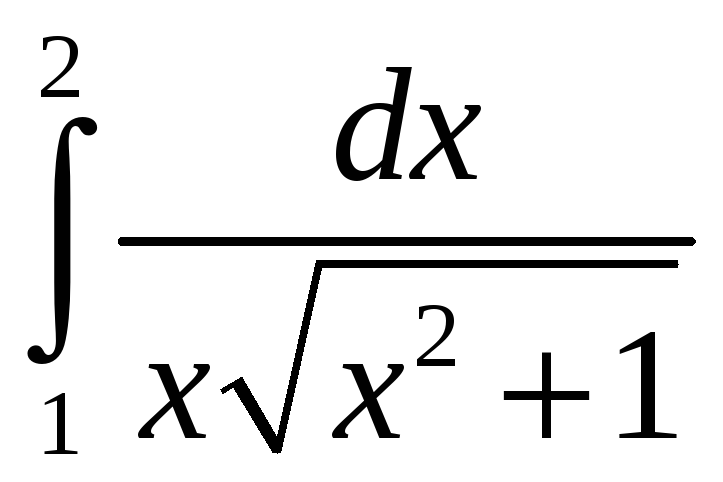
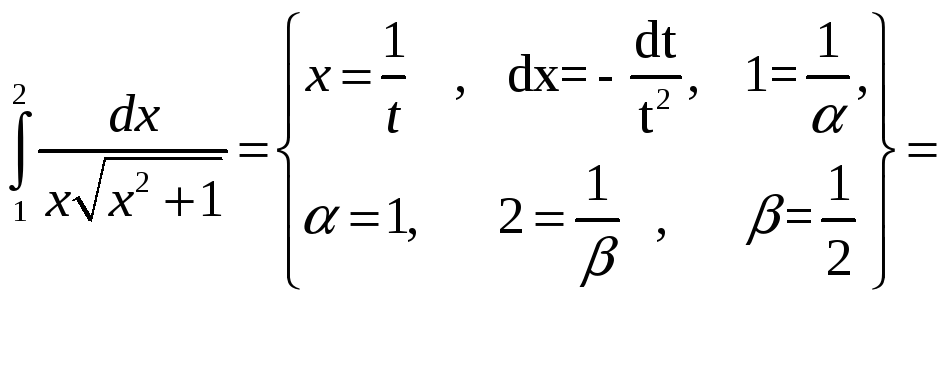
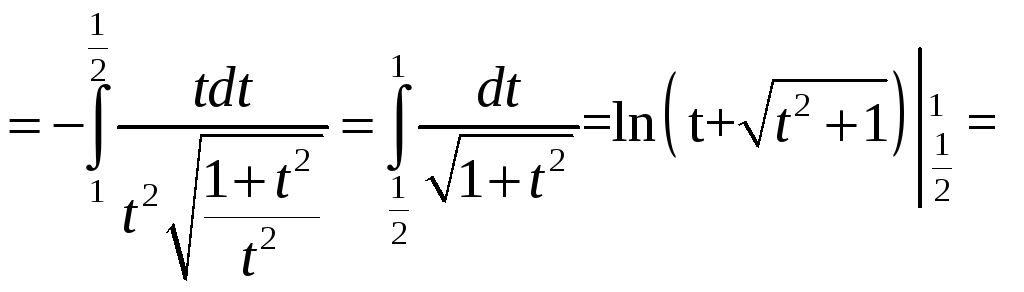
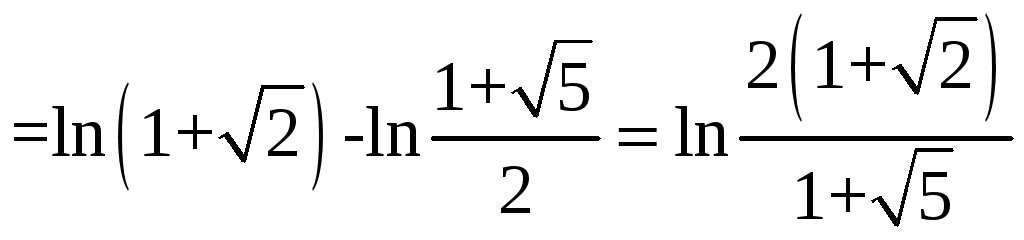 .
.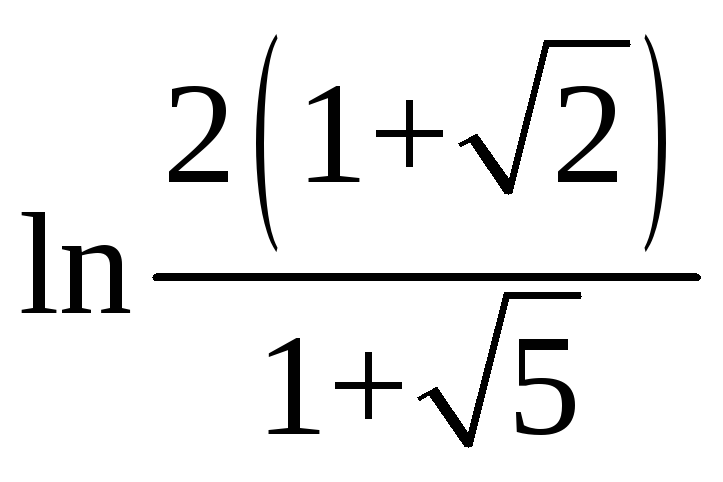
 .
.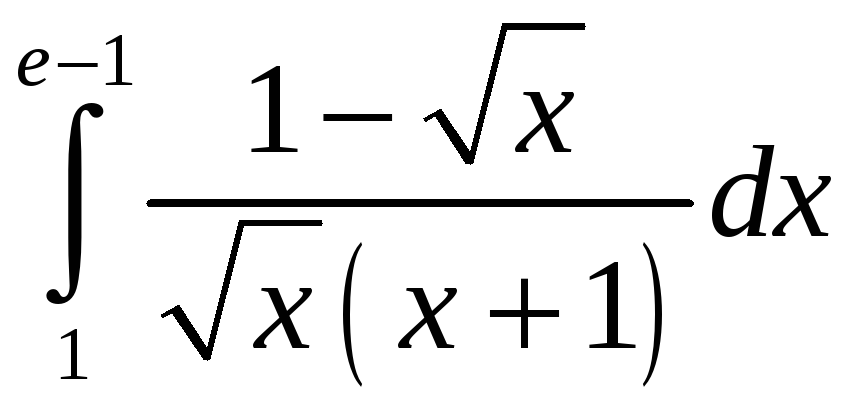 =
=
 =
=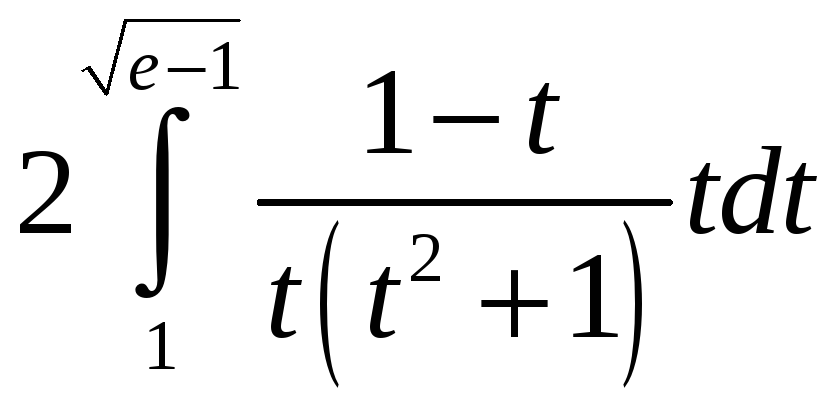 =
=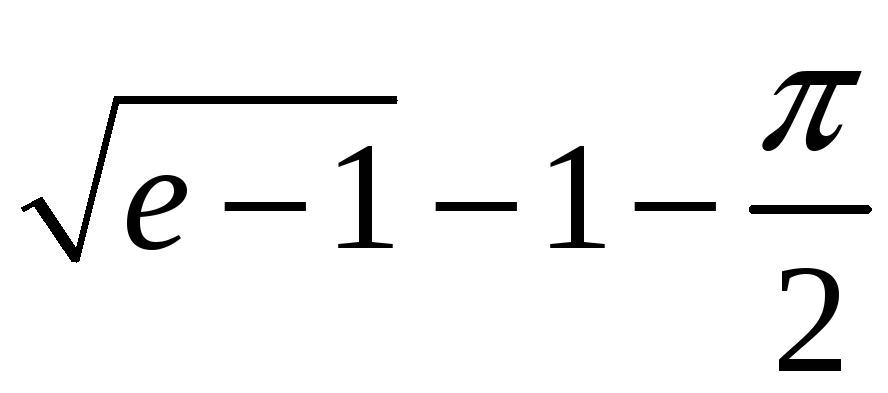 +
ln
2
0,04.
+
ln
2
0,04.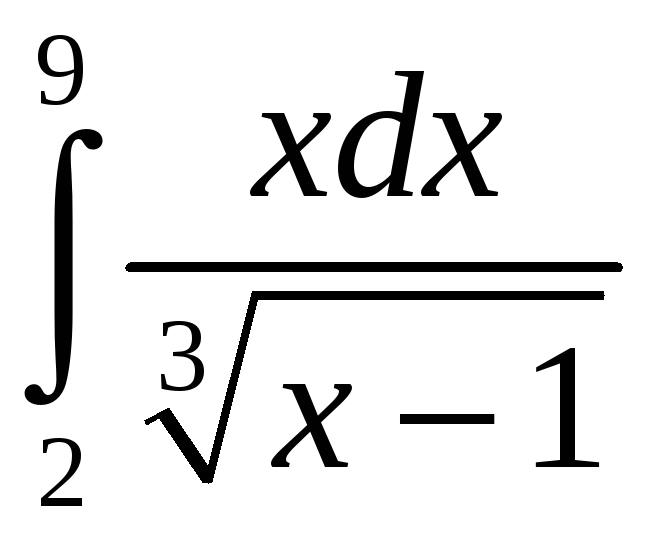 .
.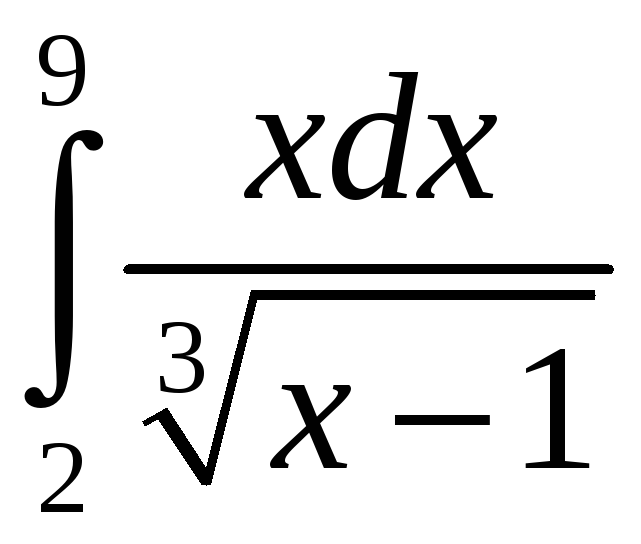 =
=
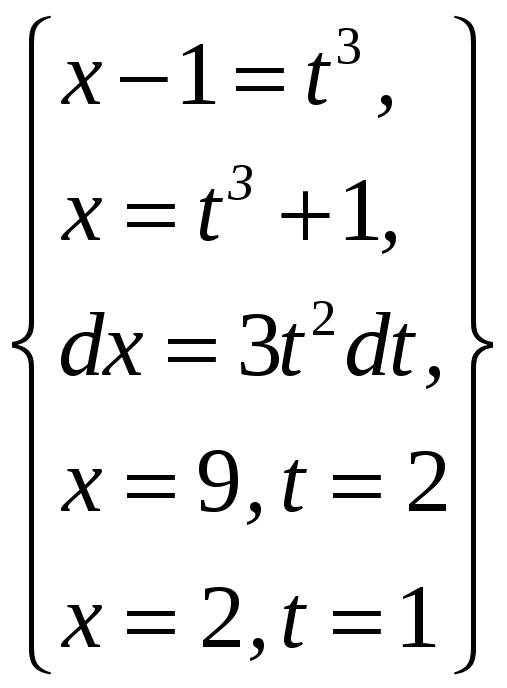 =
=

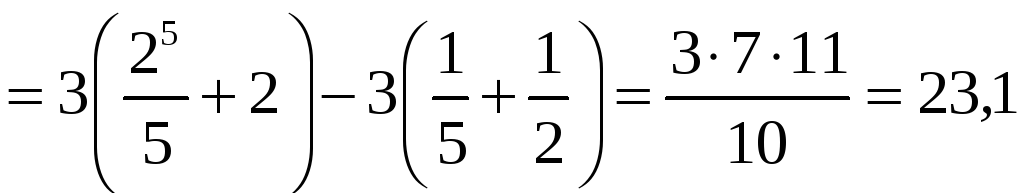 .
.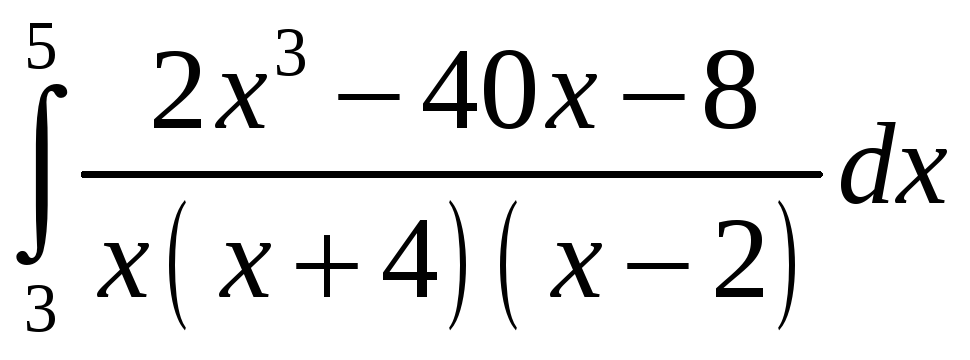 .
. =
=
 =
=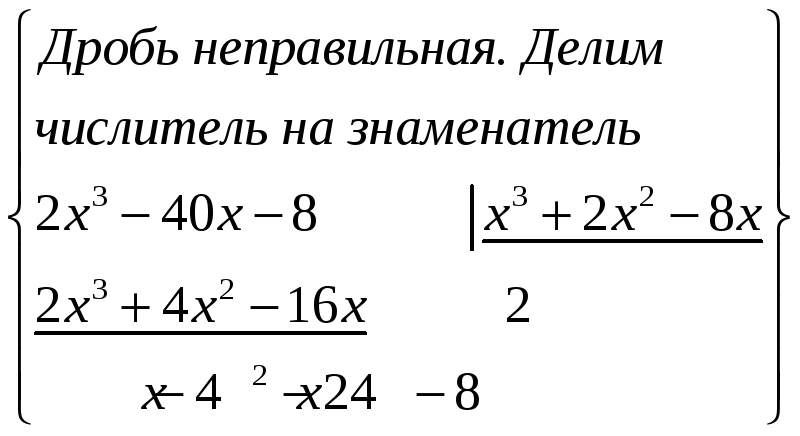
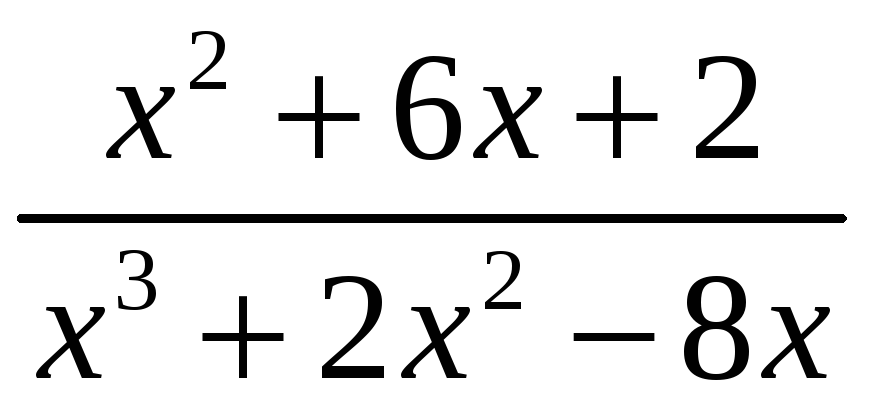 .
.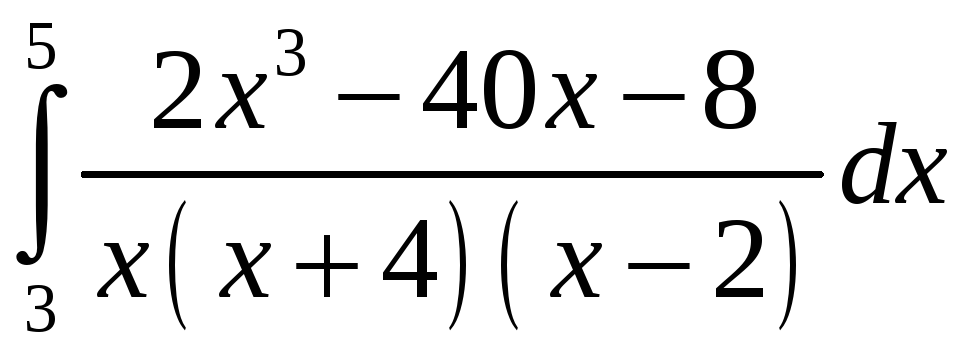 =
=
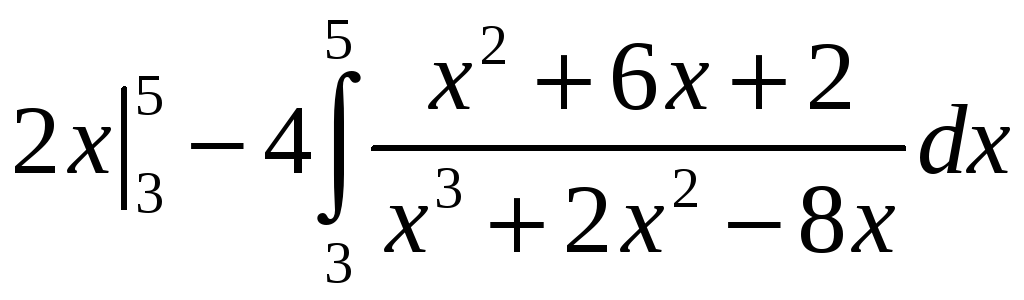 .
.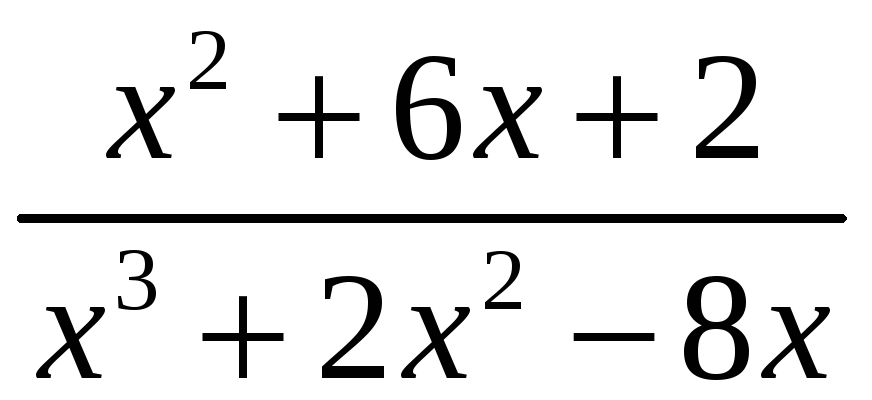 =
=
 =
=
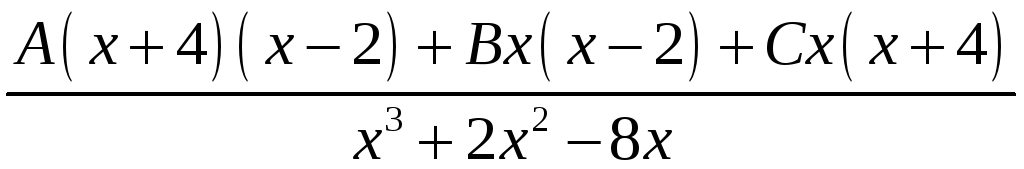 ,
,
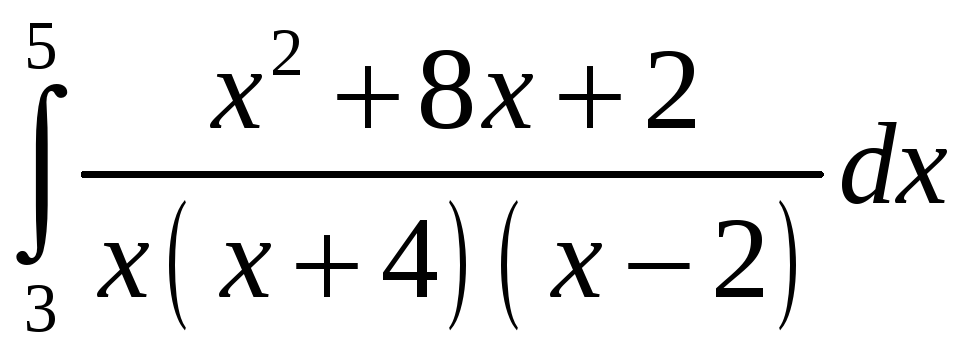 =
= =
=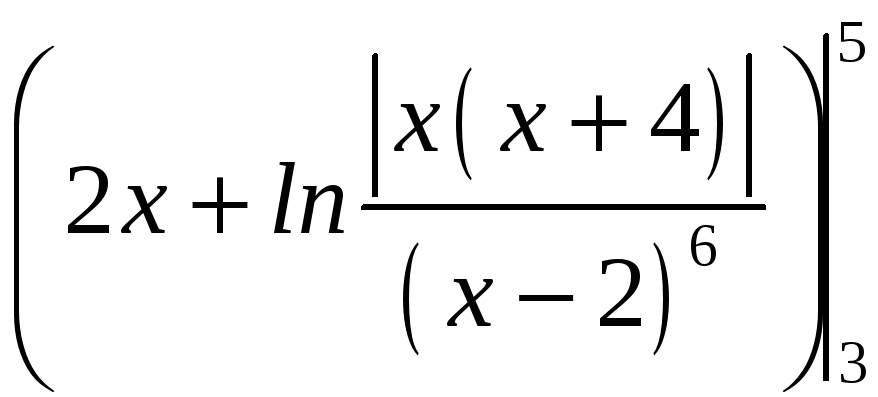 =
=
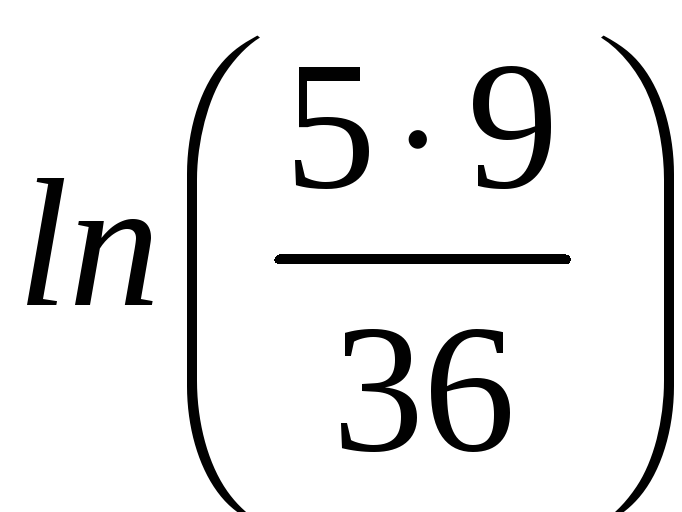
6
ln(3∙7)
=
6
ln(3∙7)
=
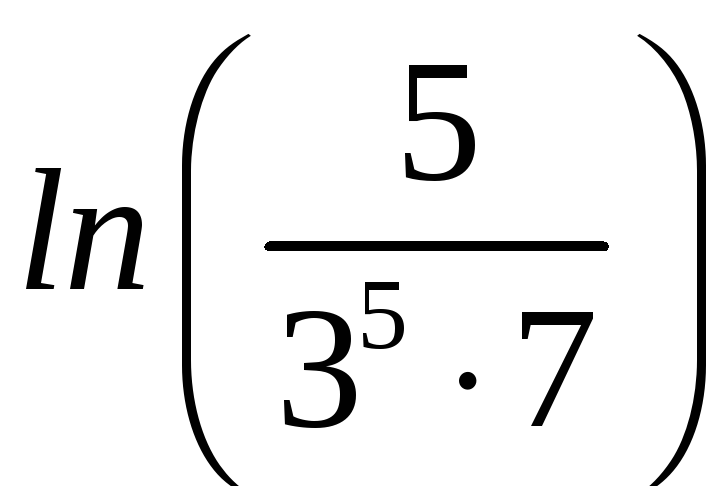
1,83.
1,83. .
.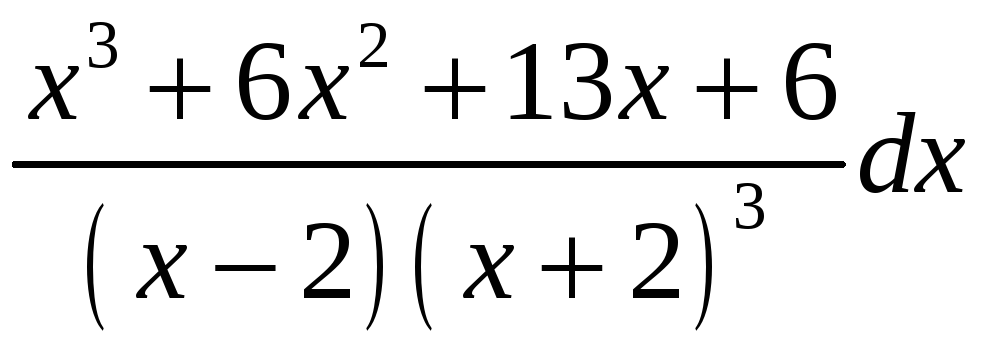 =
= =
=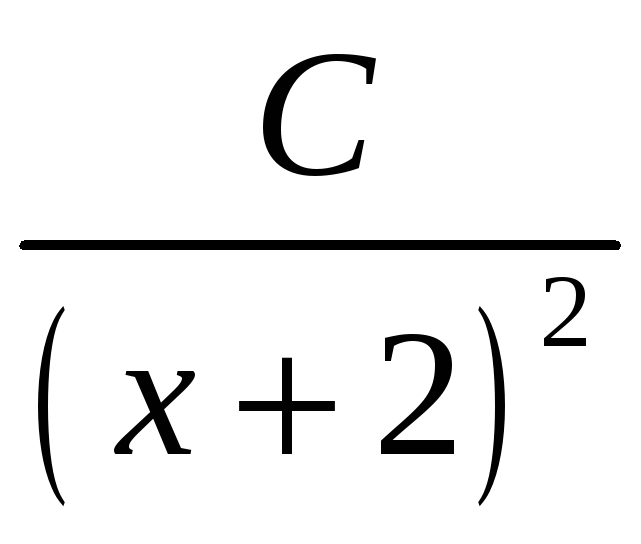 +
+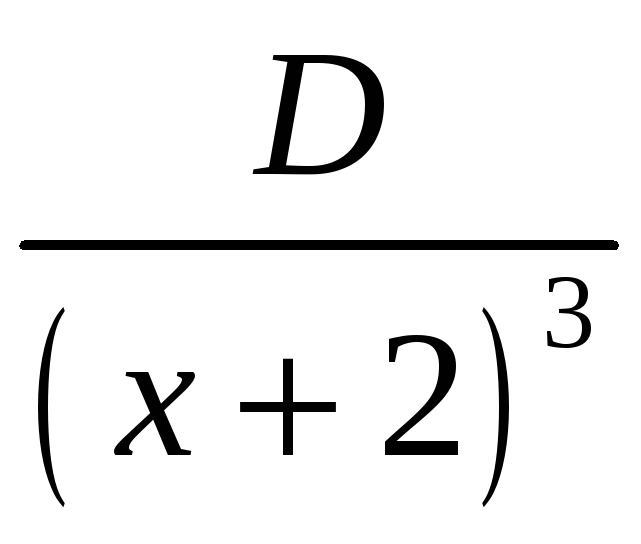 ,
,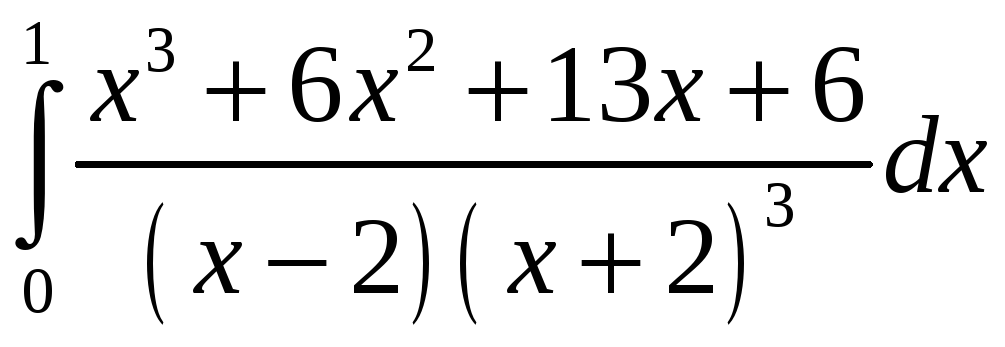 =
=
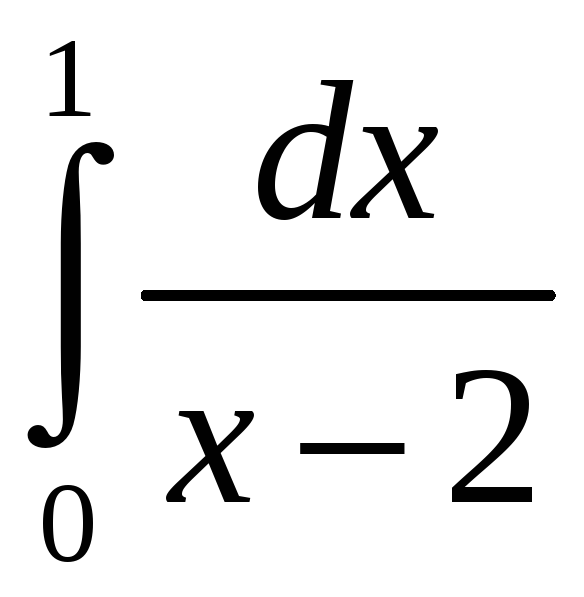 +
+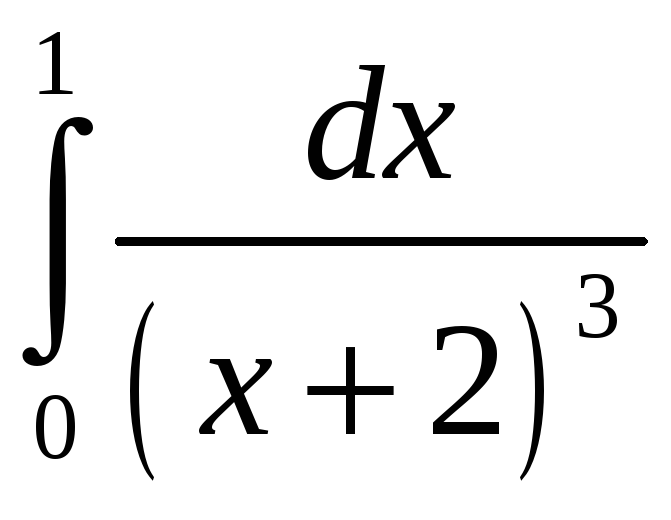 =
=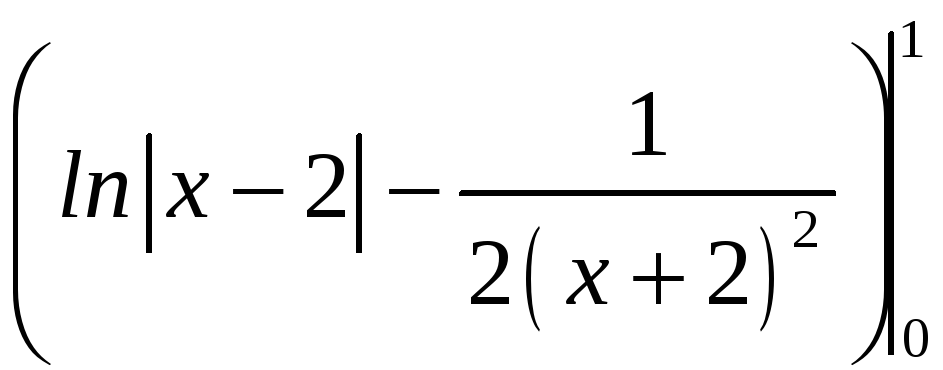 =
=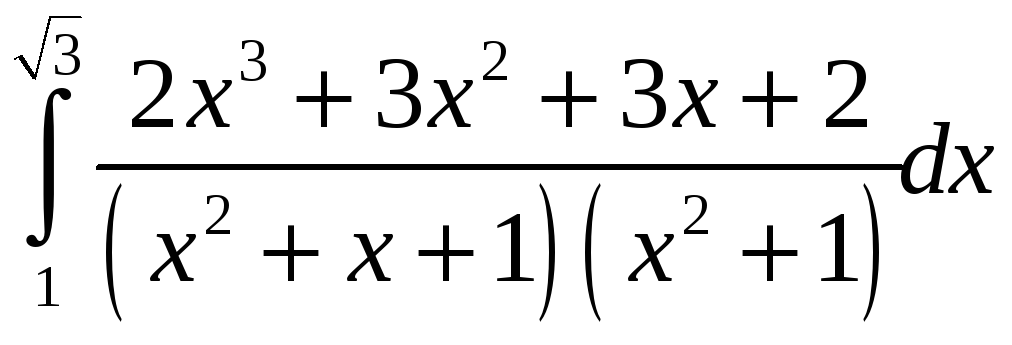 .
. =
=
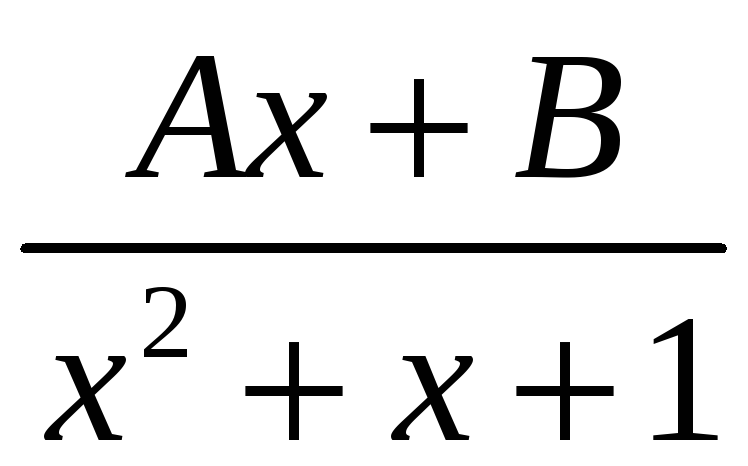 +
+
 ,
откуда
,
откуда
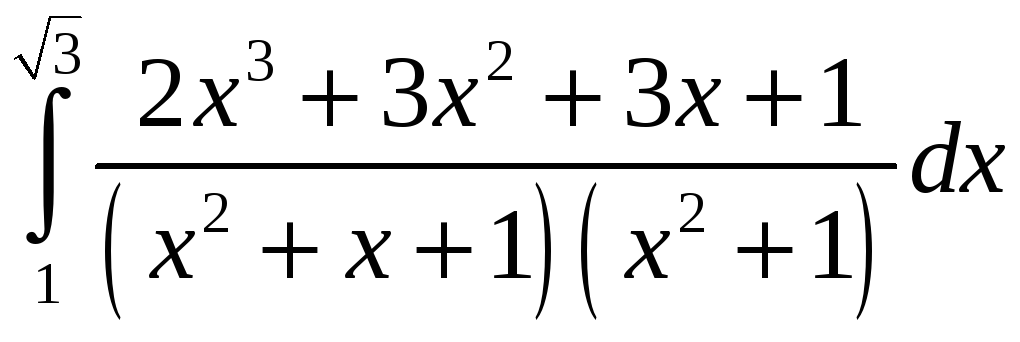 =
=
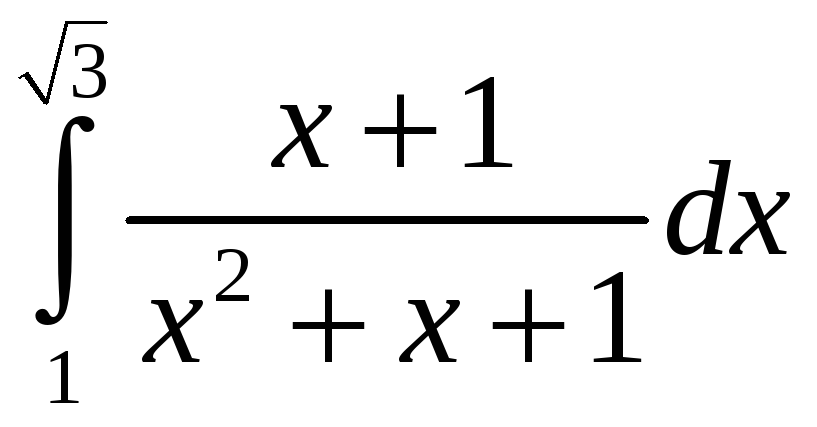 +
+
+
+
 =
=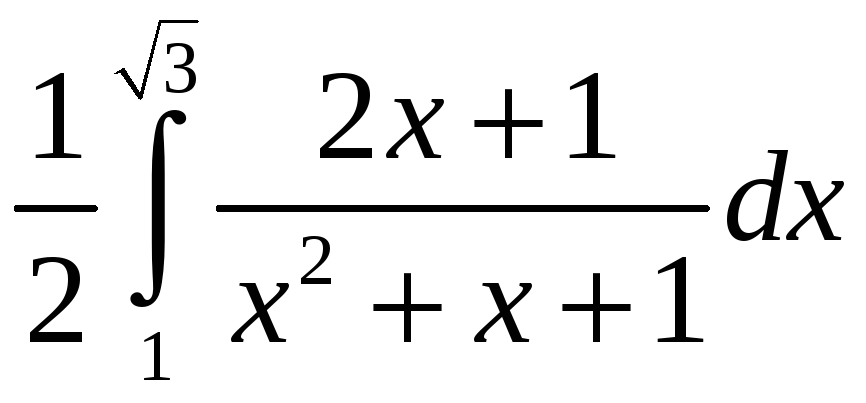 +
+
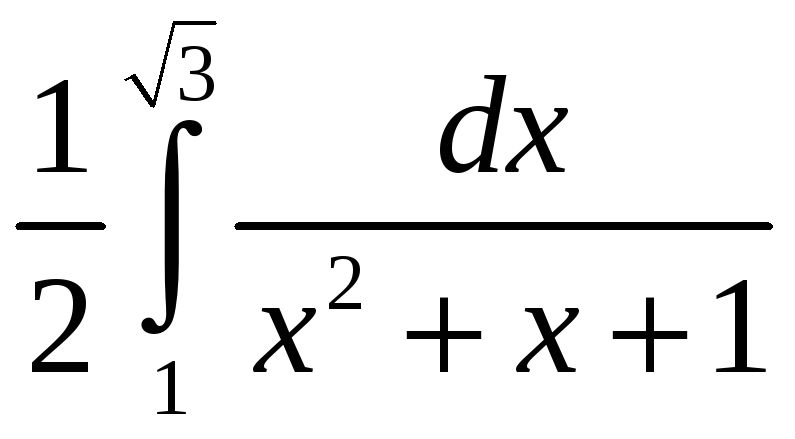 +
+
 =
=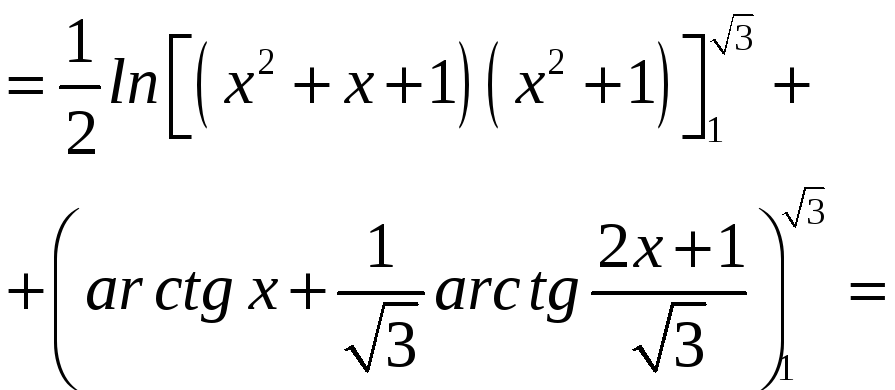
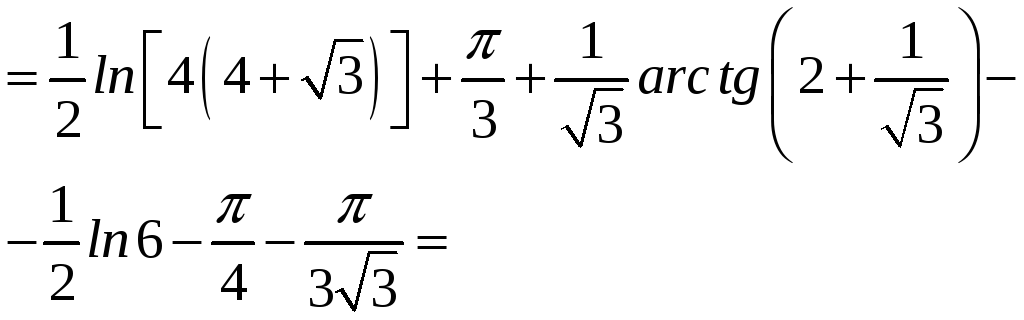
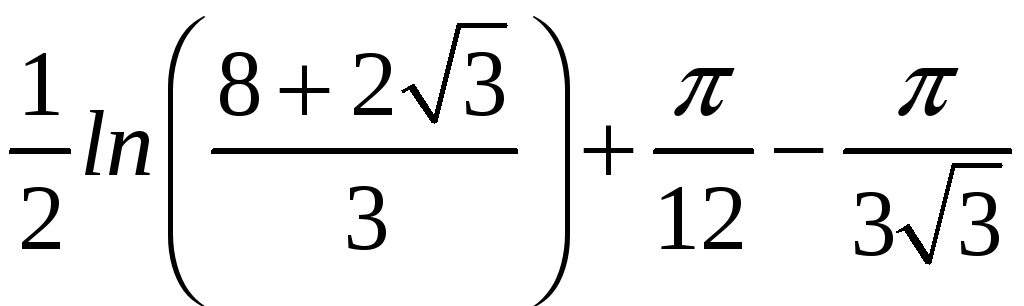 +
+
+
+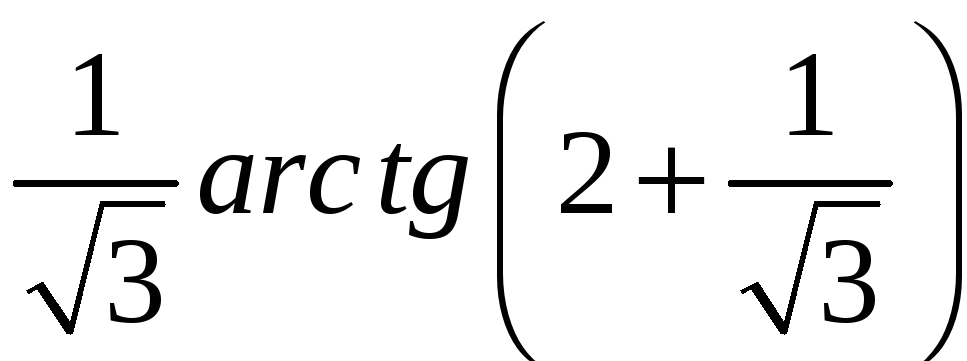
1,02.
1,02. .
.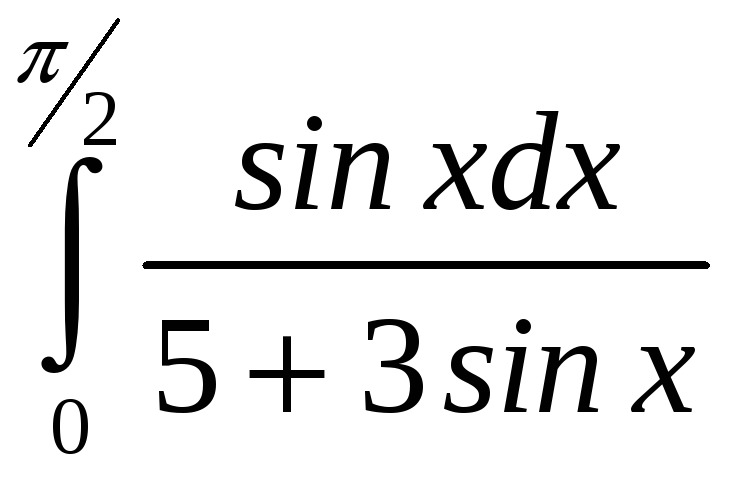 =
=
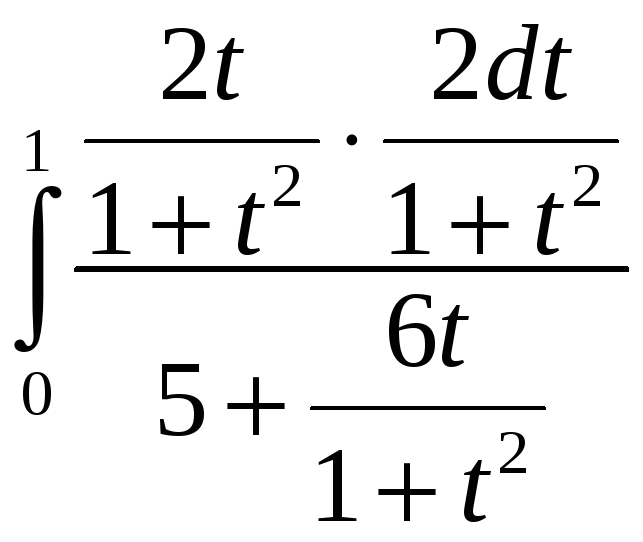 =
= .
.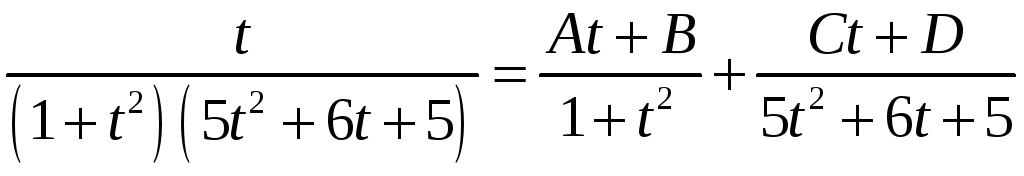 ,
,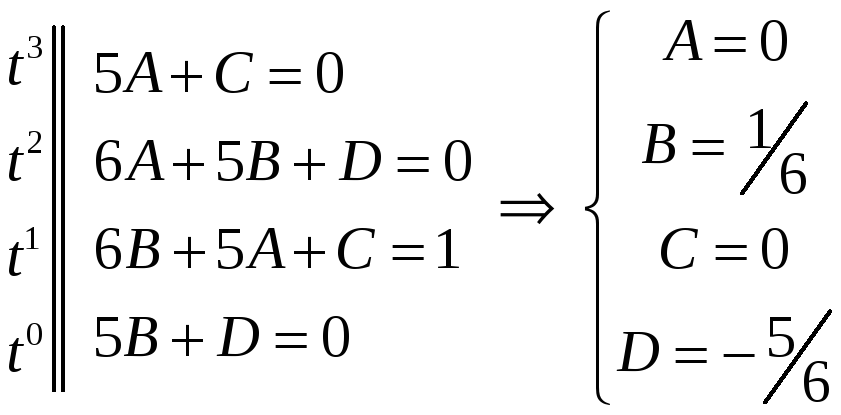
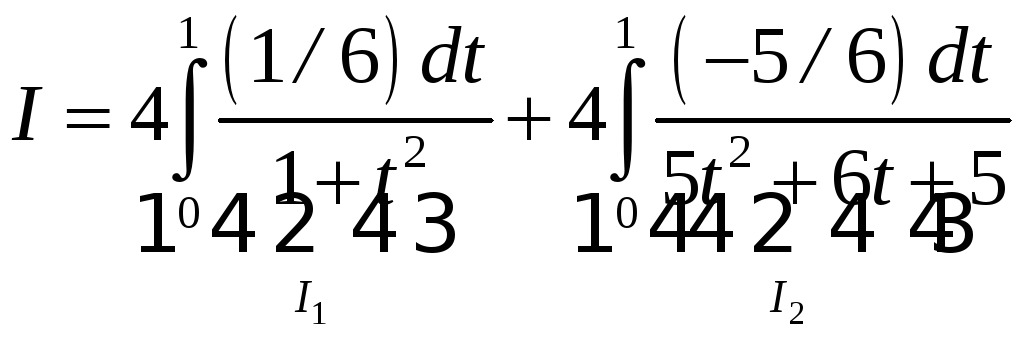
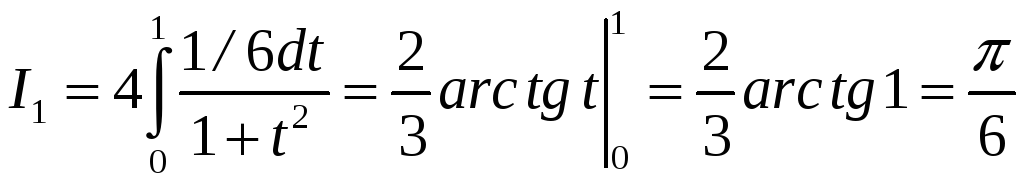 ,
,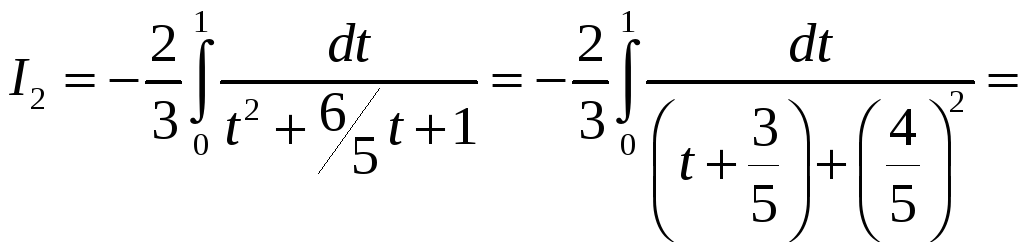
 .
.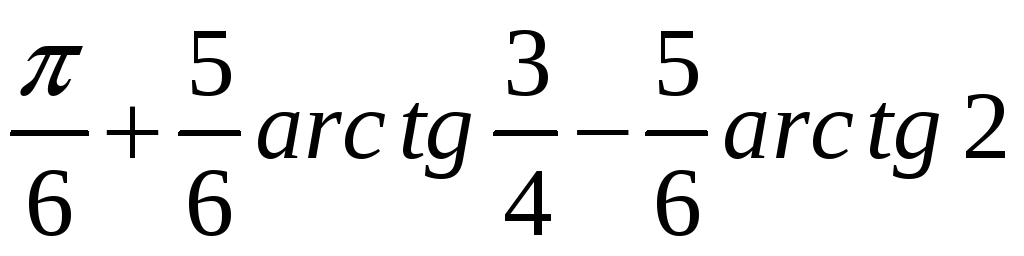
0,14.
0,14.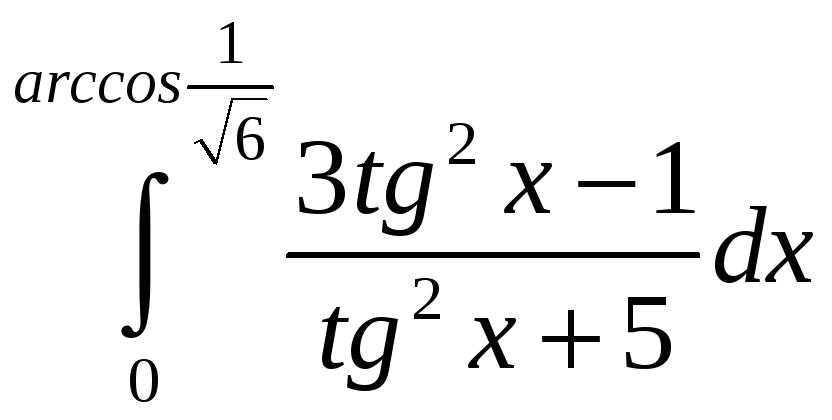 .
.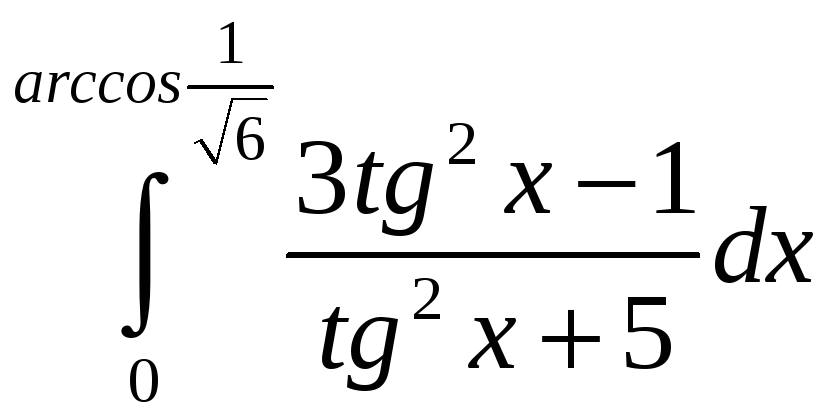 =
=

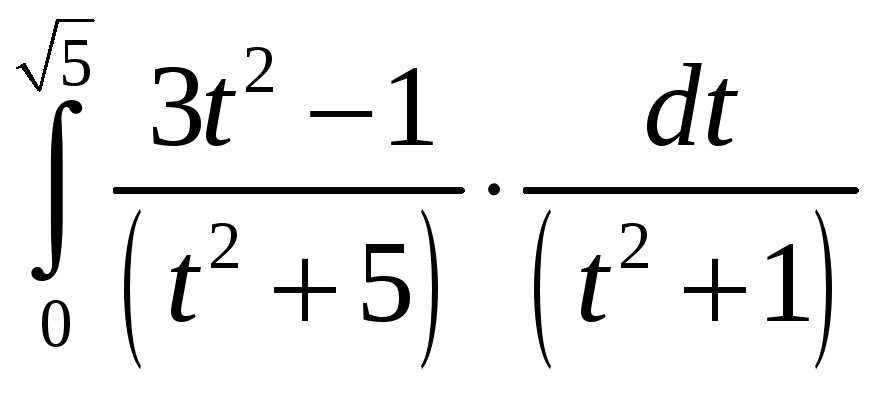 .
.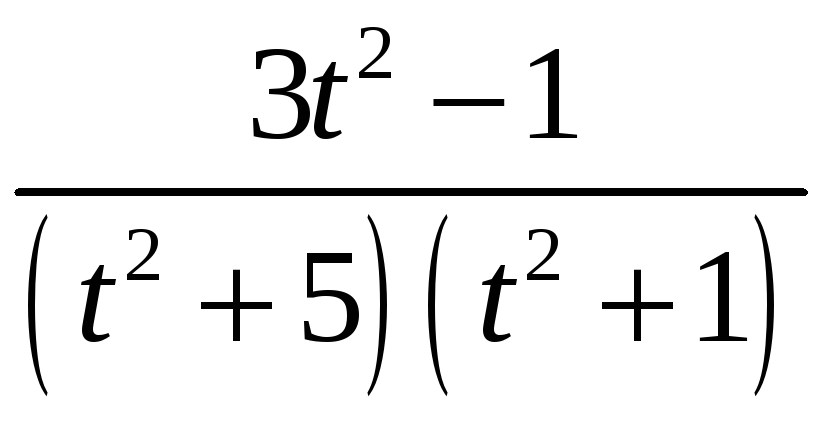 =
=
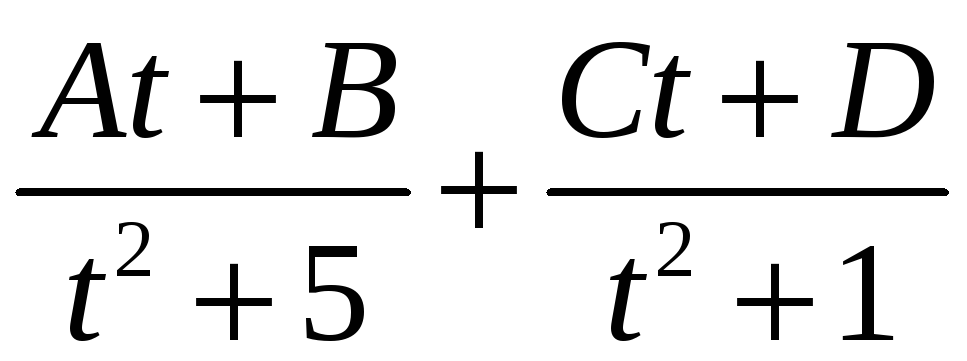 ,
,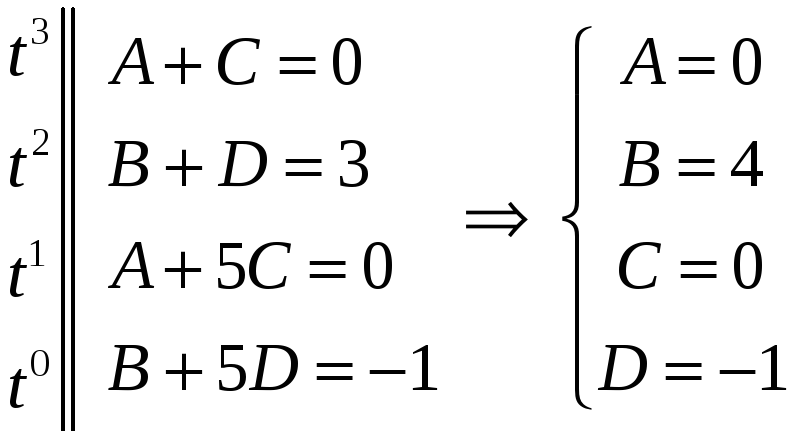
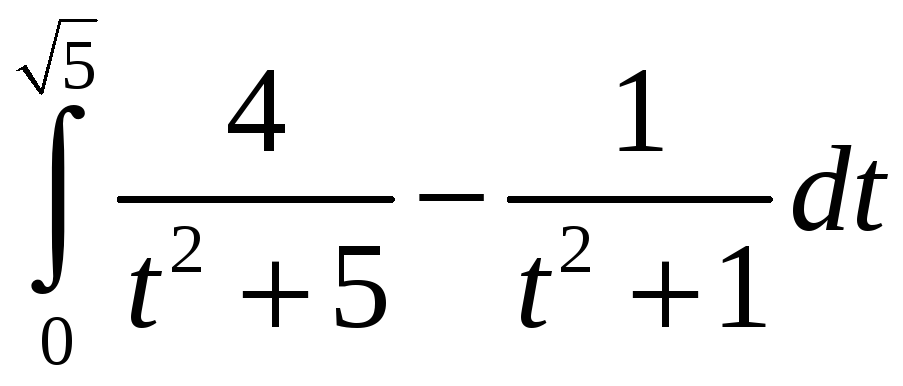 =
=
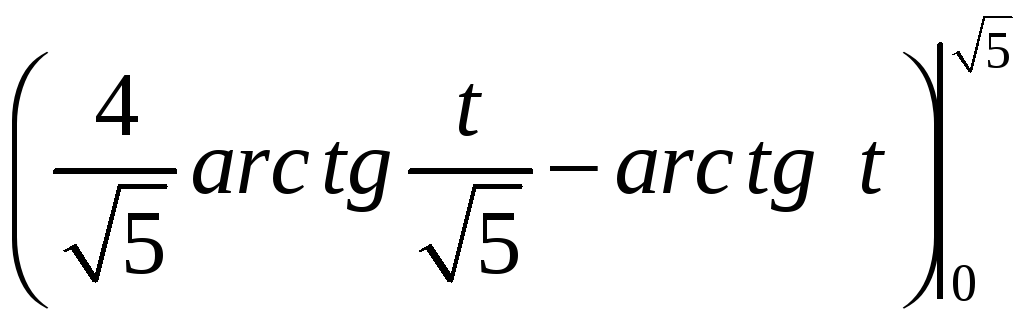 =
=
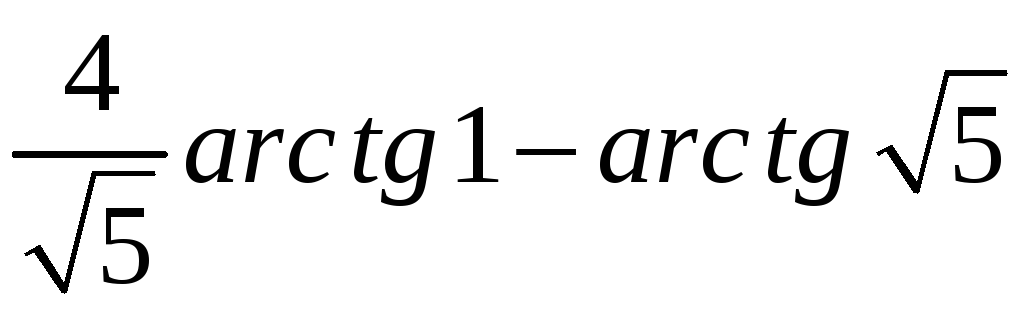 =
=
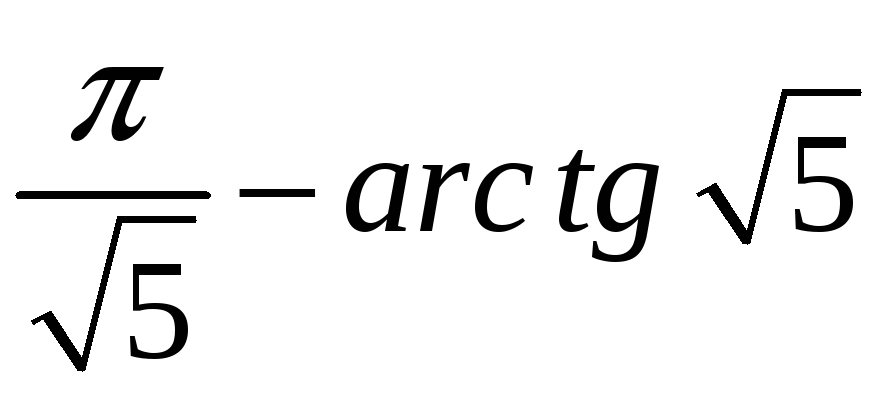
0,25.
0,25.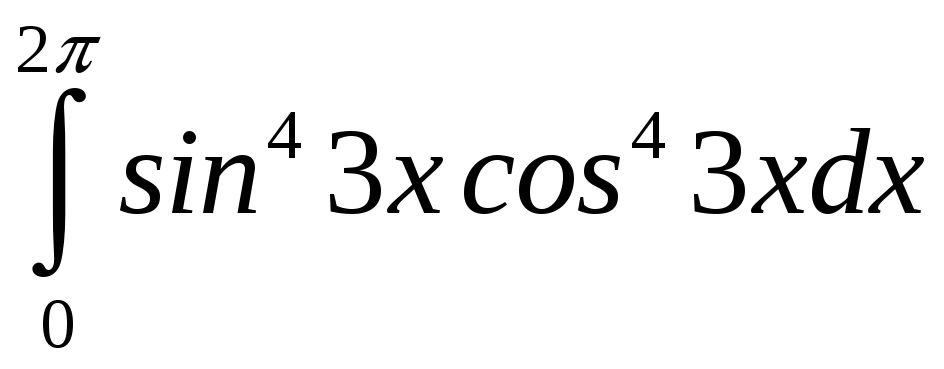 .
.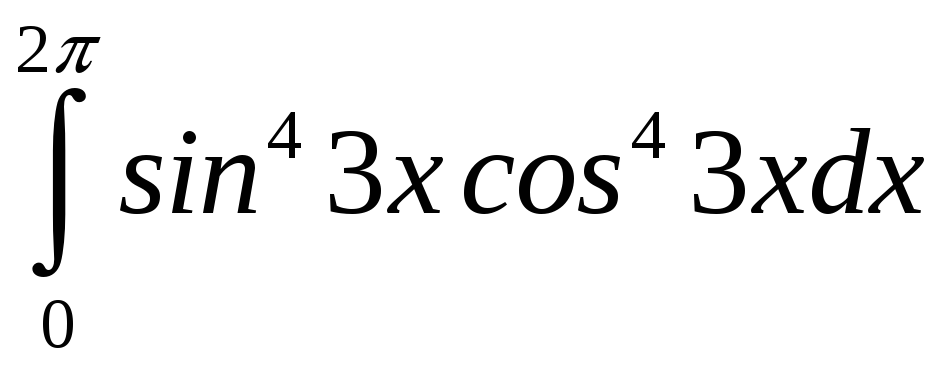 =
=
 =
=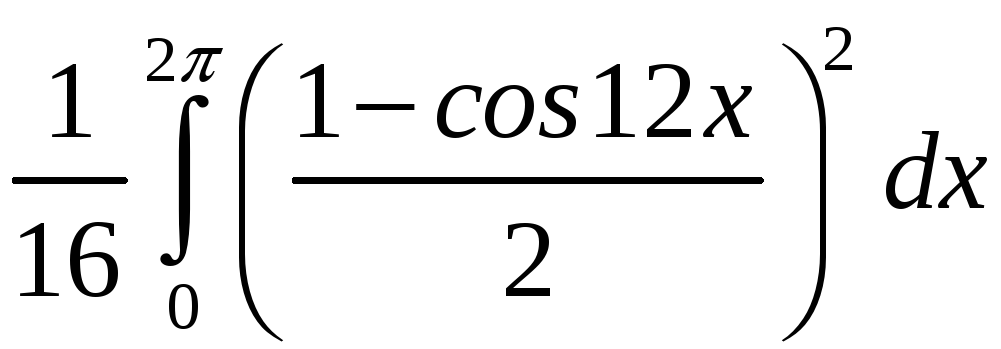 =
=
=
= =
=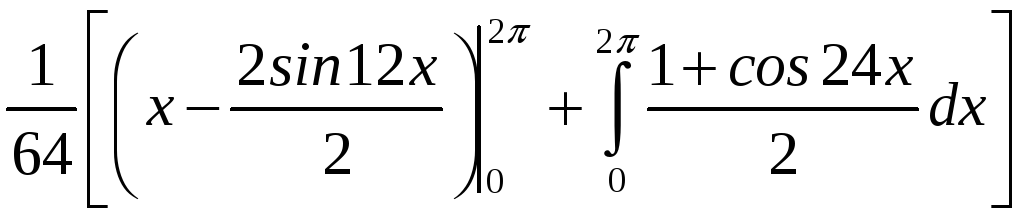 =
=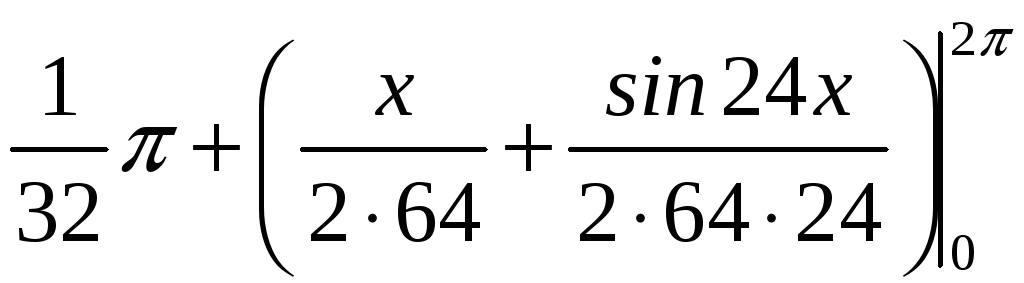 =
=
 .
. =
=
 =
=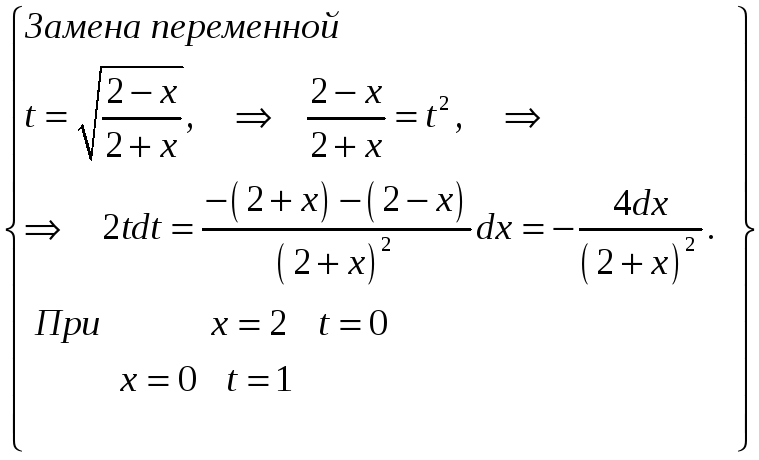
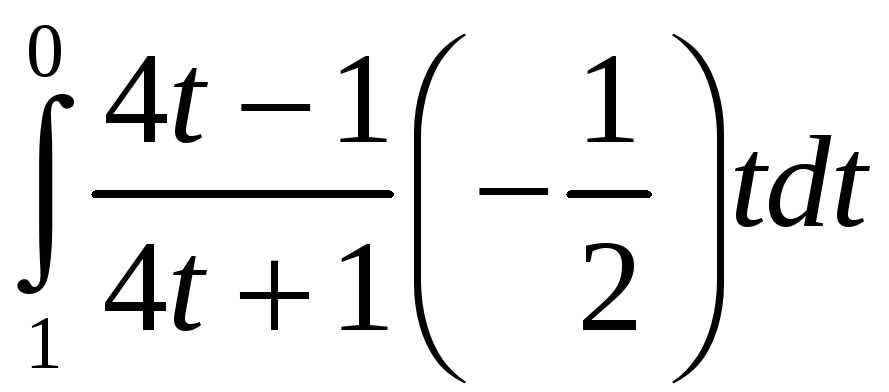 =
=
 .
.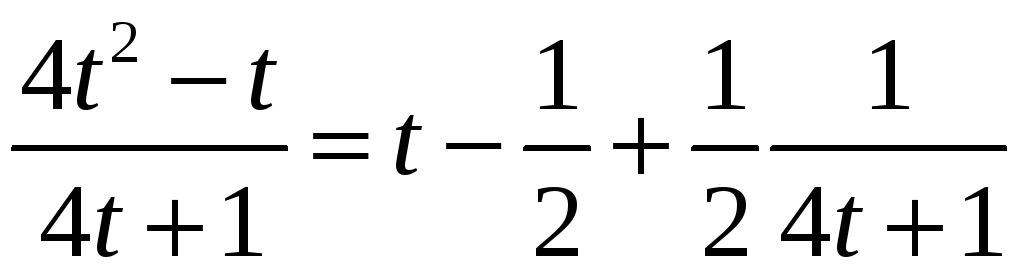 .
.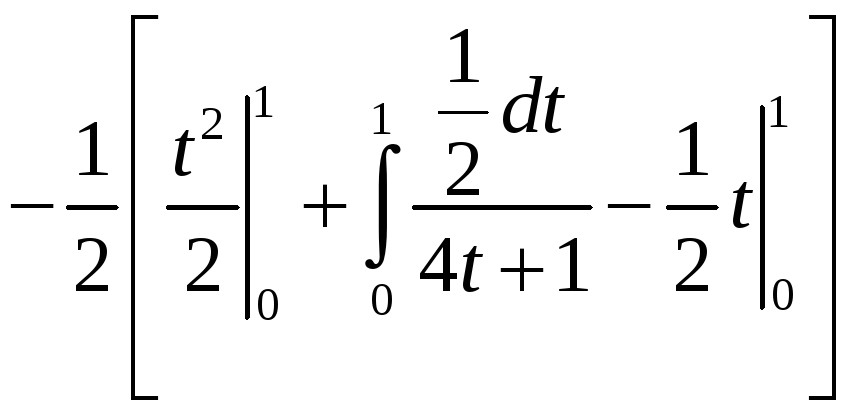 =
=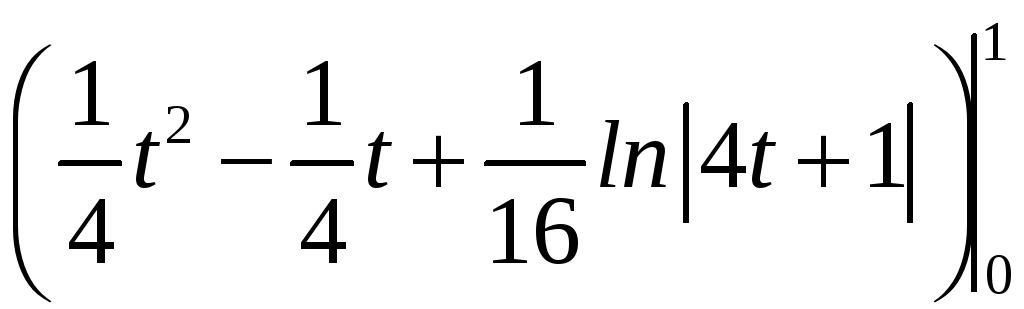 =
=
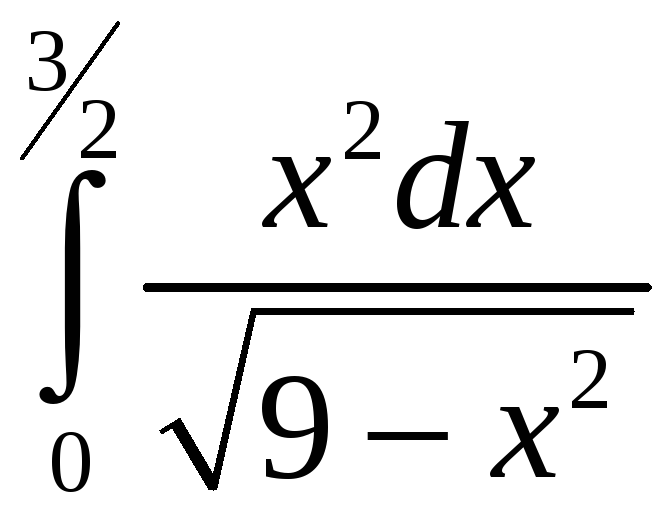 .
.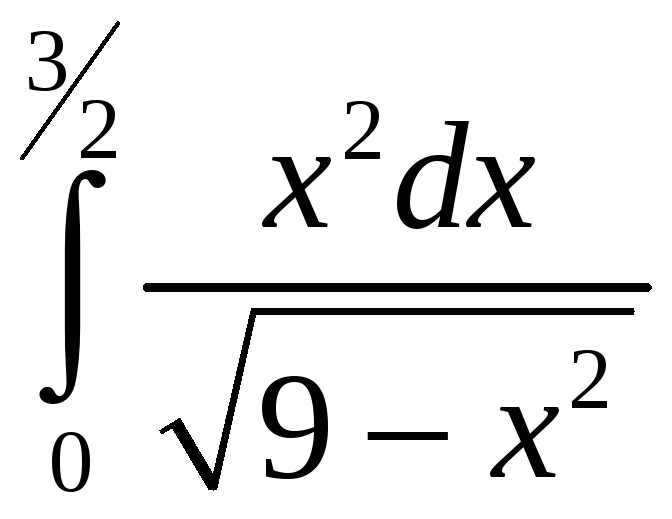 =
=
 =
=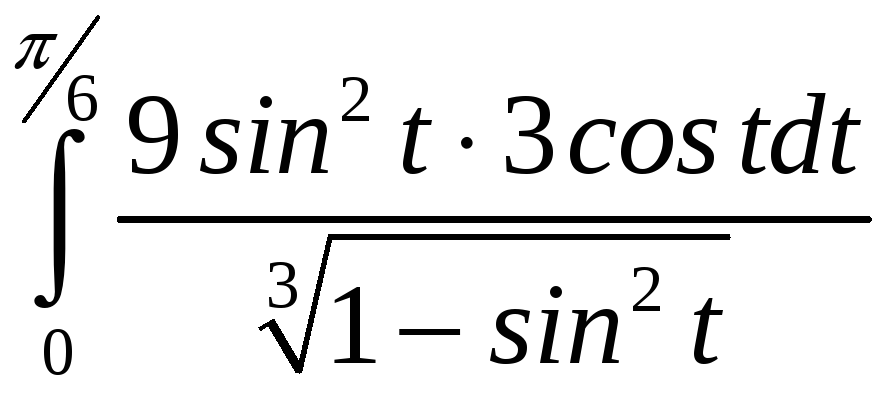 =
= =
=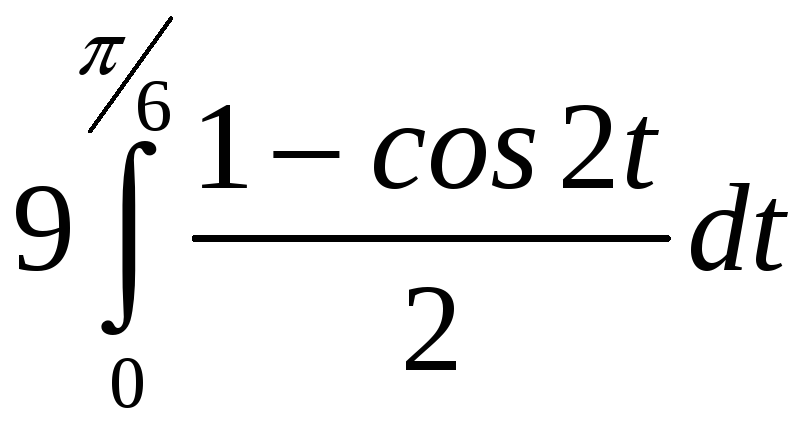 =
=
 =
=
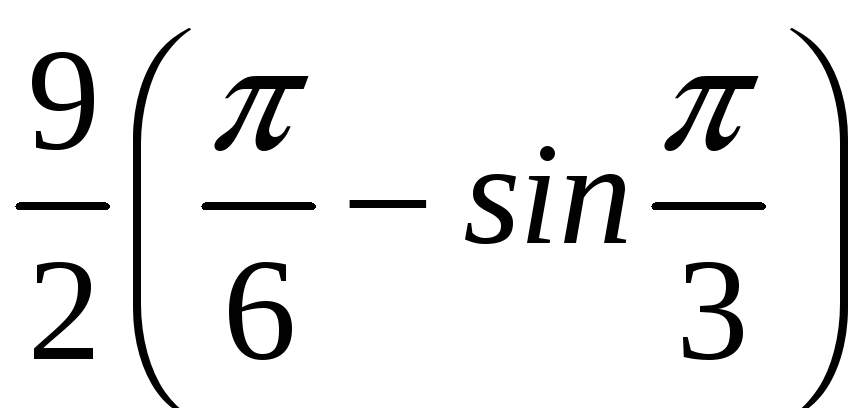 =
=
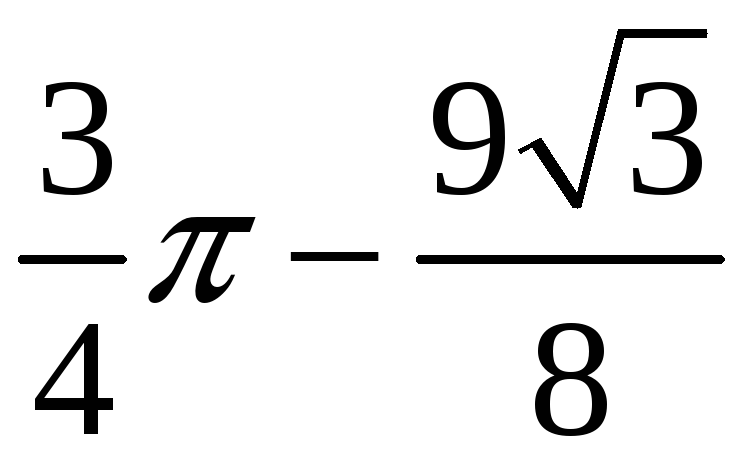
0,4.
0,4. .
.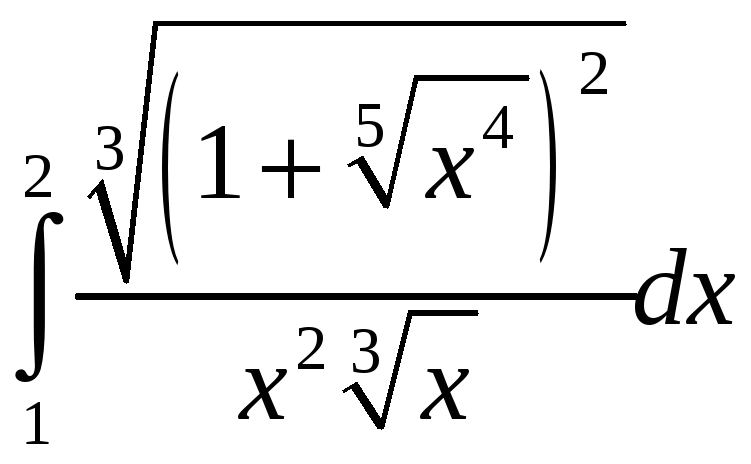 =
=
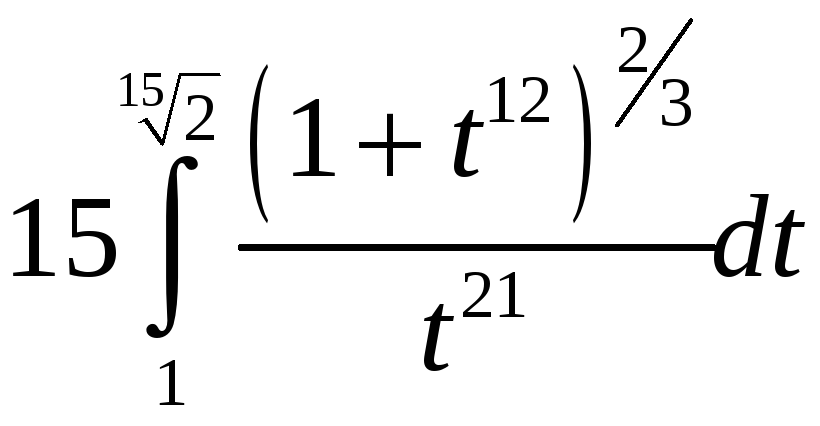 = =
= =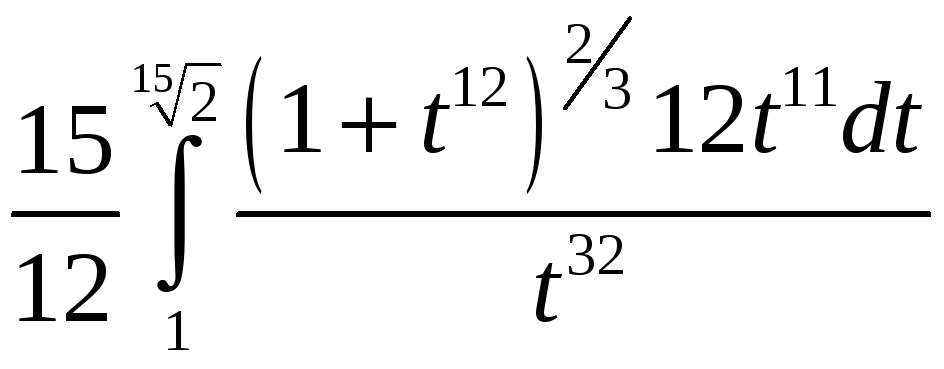 =
=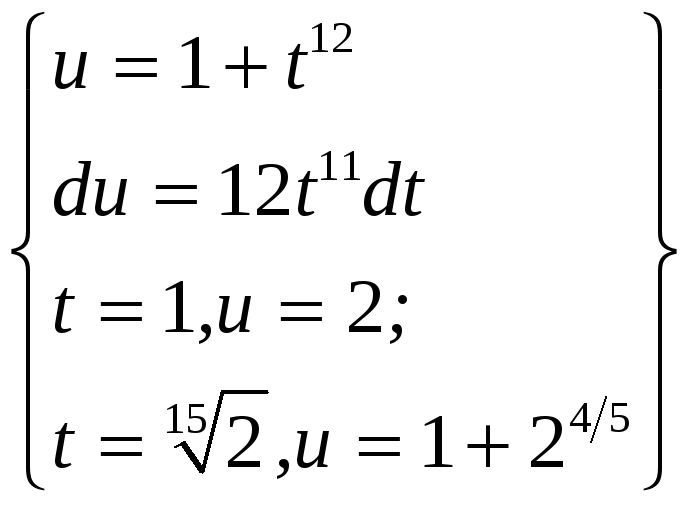
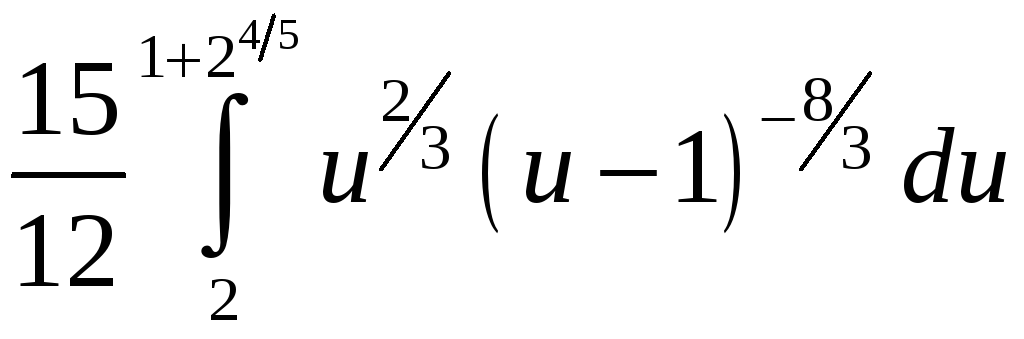 =
=
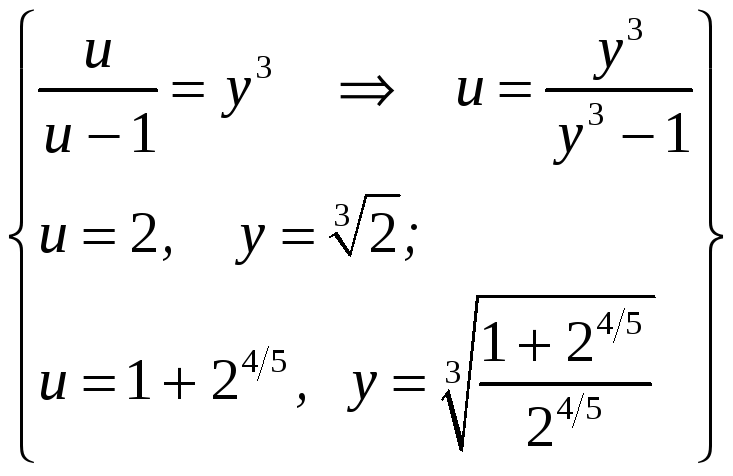
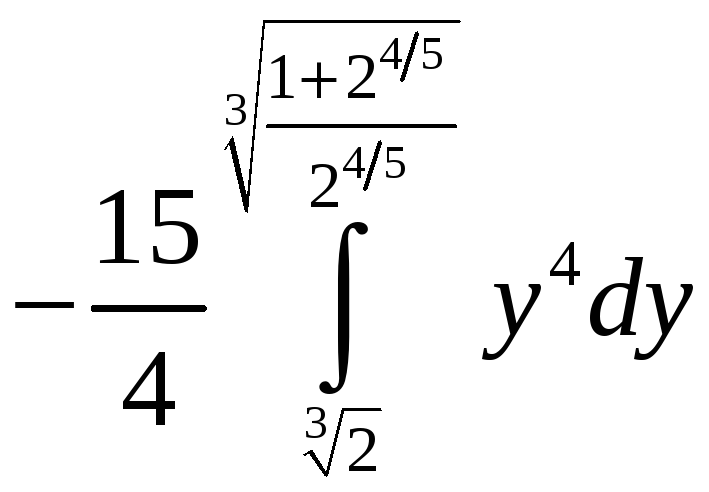 =
=
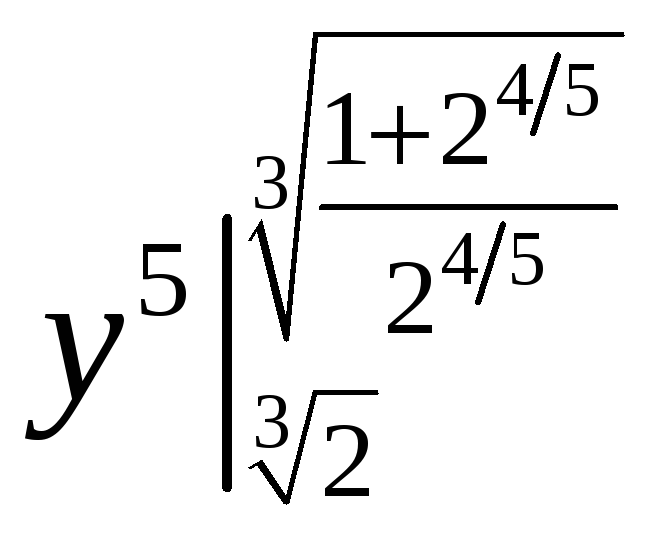 = =
= =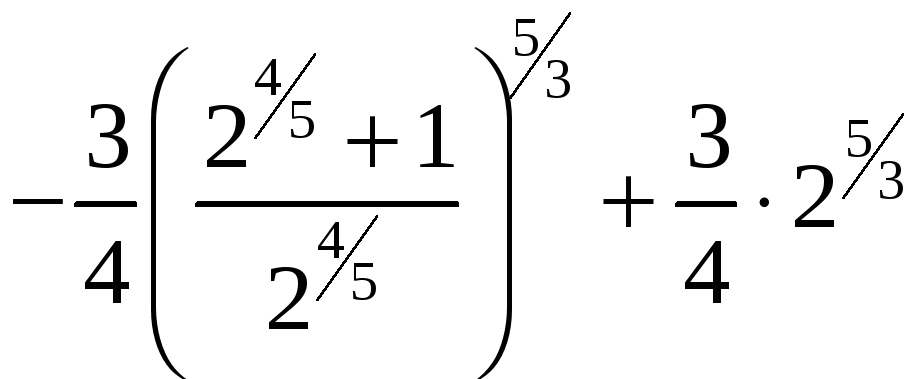
0,78.
0,78.