
ПП 22. Геометрические приложения определенного интеграла
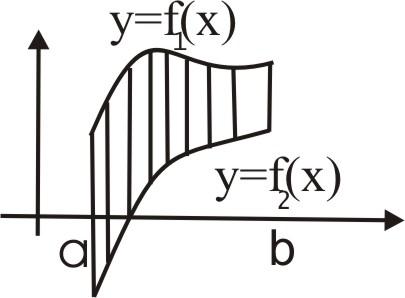
1. Вычисление площадей плоских фигур
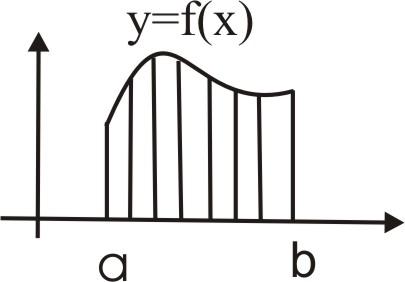
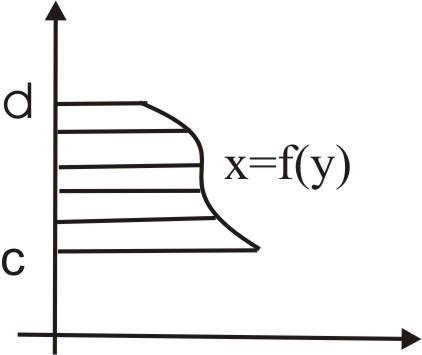
1.1. Вычисление площади в прямоугольных координатах
|
1)
|
|
|
2)
|
|
|
3)
|
|
1.2. Вычисление площадей фигур, заданных кривыми в параметрическом виде
Если кривая задана параметрическими уравнениями:
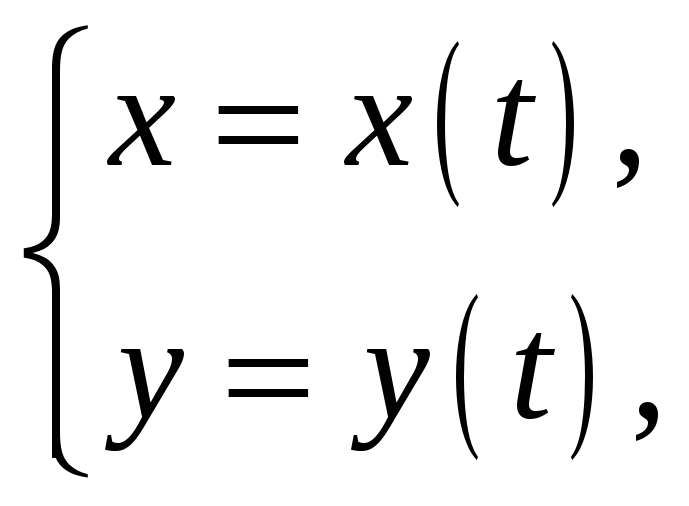
![]() ,
,
![]() ,
,
![]() .
.
 .
.
1.3. Площадь фигуры, заданной в полярной системе координат
|
Если
|
|
2. Вычисление длины дуги кривой
2.1. Длина плоской кривой в прямоугольных координатах
![]() ,
,
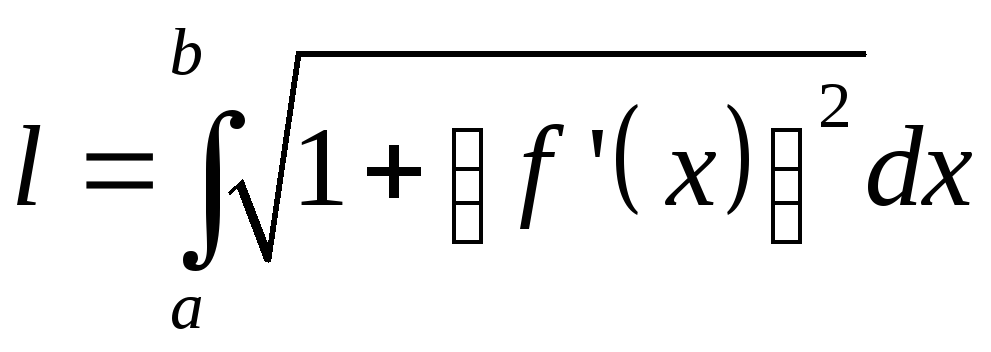 .
.
2.2. Длина плоской и пространственной кривой, заданной в параметрическом виде
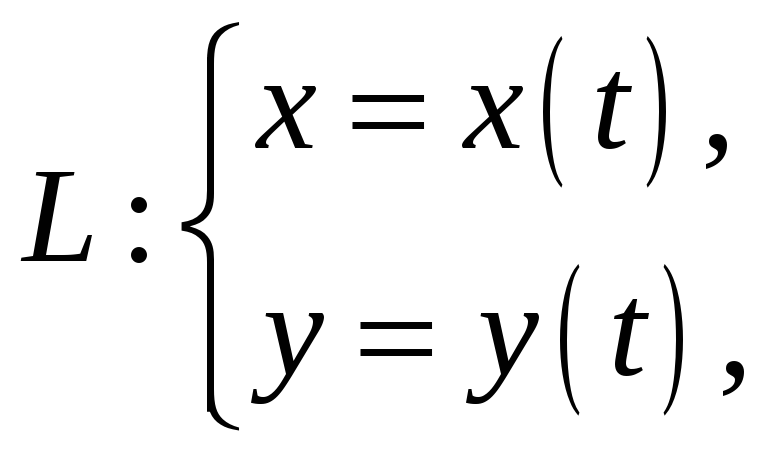
![]()
![]() ,
,
 ;
;
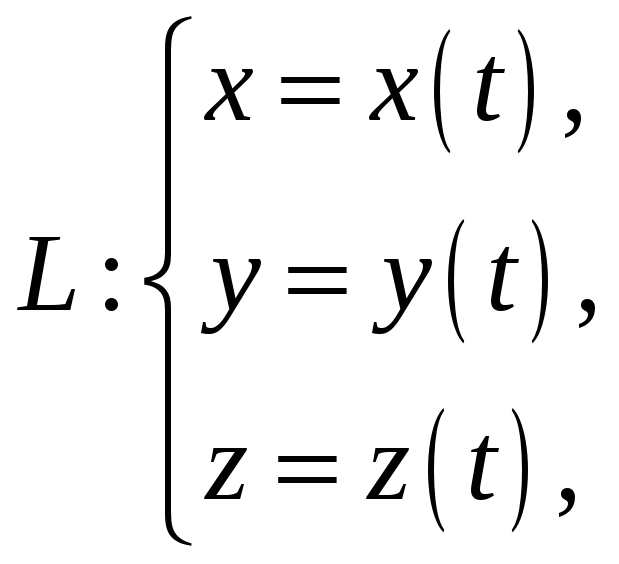
![]() ,
,
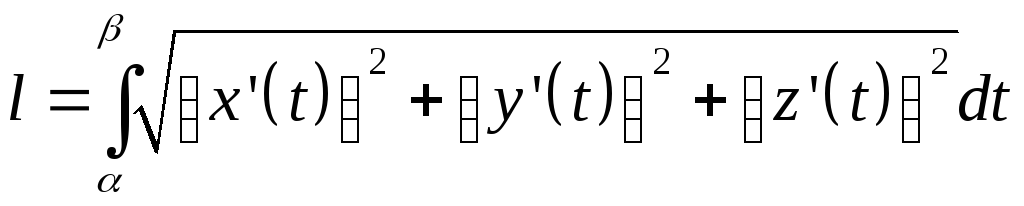 .
.
2.3. Длина кривой, заданной в полярных координатах
![]()
![]() ,
,
![]() ,
,
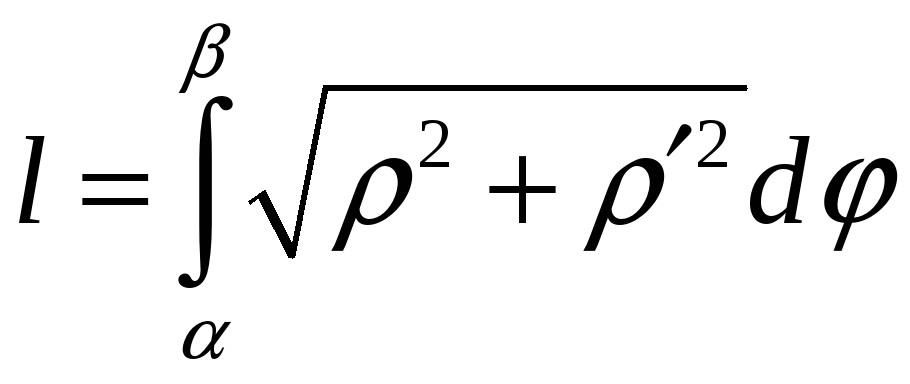 .
.
3. Площадь поверхности вращения
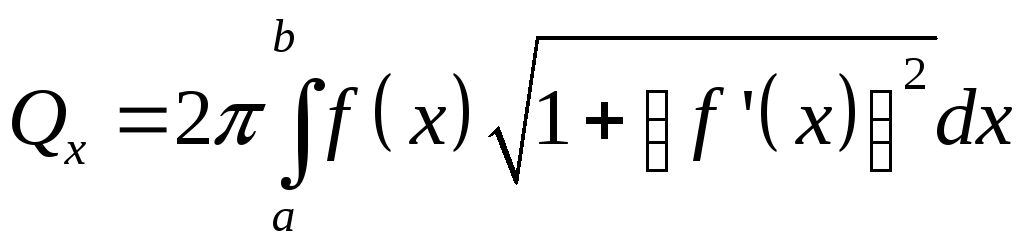 -
площадь поверхности, образованной
вращением кривой, заданной функцией у
=
-
площадь поверхности, образованной
вращением кривой, заданной функцией у
=
![]() ,
а
х
b
.
,
а
х
b
.
Если
дуга задана параметрическими уравнениями
х
= х
(t),
у
= у (t),
t1
t
t2
,
то Qх
= 2
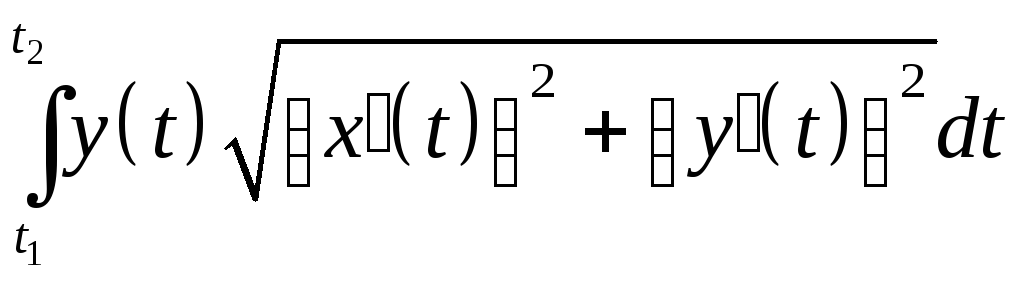 .
.
Если
дуга задана в полярных координатах
=
(),
,
то Qх
= 2
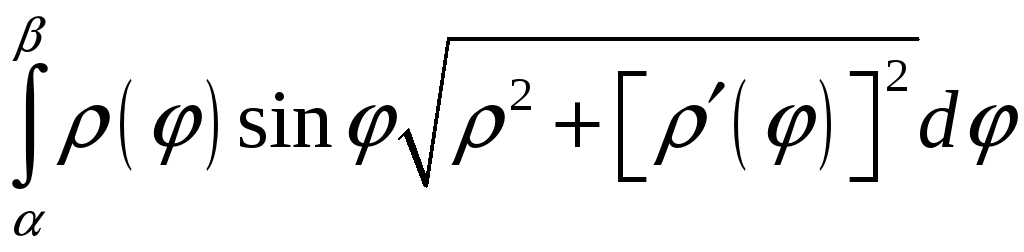 .
.
4. Вычисление объемов тел
4.1. Вычисление объемов по заданным площадям поперечных сечений
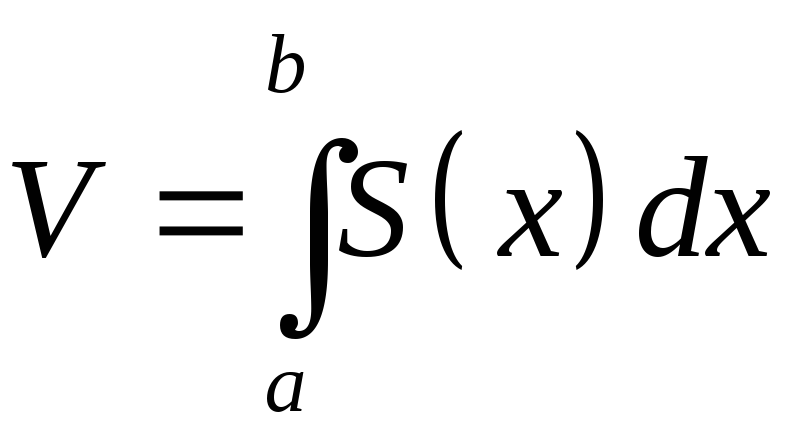 ,
,
![]() - площадь поперечного сечения.
- площадь поперечного сечения.
4.2. Вычисление объемов тел вращения
Если
криволинейная трапеция, ограниченная
кривой у
=
![]() ,
а
х
b,
вращается вокруг оси Ох,
то объём тела вращения вычисляется по
формуле:
,
а
х
b,
вращается вокруг оси Ох,
то объём тела вращения вычисляется по
формуле:
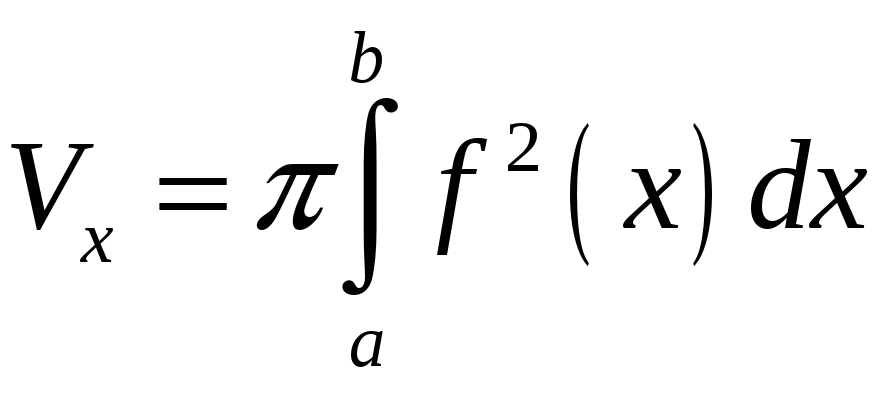 .
.
Если
криволинейная трапеция, ограниченная
кривой
![]() ,
c
y
d,
вращается вокруг оси Оу,
то
,
c
y
d,
вращается вокруг оси Оу,
то
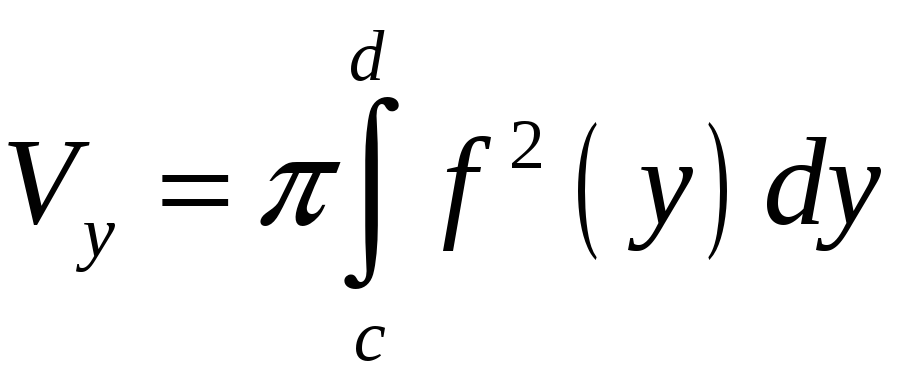 .
Величина
Vу
может быть также вычислена интегрированием
по х:
Vу
=
.
Величина
Vу
может быть также вычислена интегрированием
по х:
Vу
=
 .
.
5. Приложеия определенного интеграла к решению некоторых задач механики и физики
5.1. Моменты и центры масс плоских кривых
Статические
моменты дуги кривой, заданной уравнением
![]() с плотностью (если не указано, то
с плотностью (если не указано, то
![]() ),
относительно координатных осей Ох
и
Оу:
),
относительно координатных осей Ох
и
Оу:
 ,
,
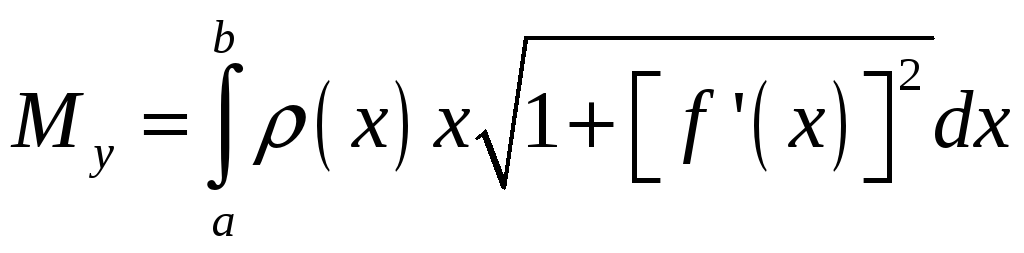 .
.
Моменты инерции
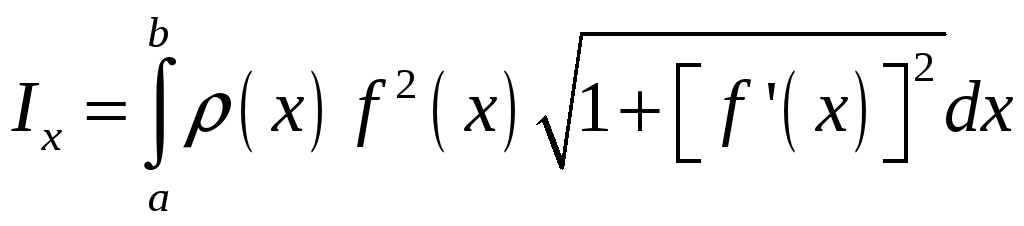 ,
,
 .
.
Координаты
центра масс
![]() и
и
![]() :
:
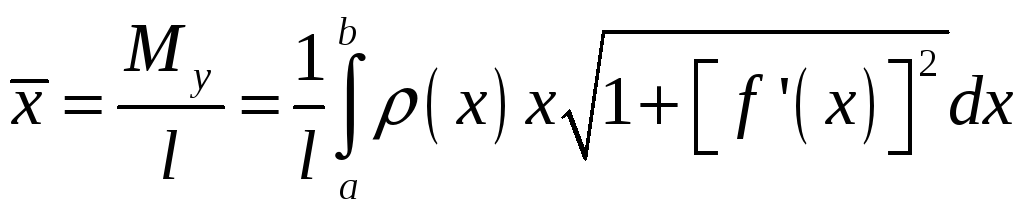 ,
,
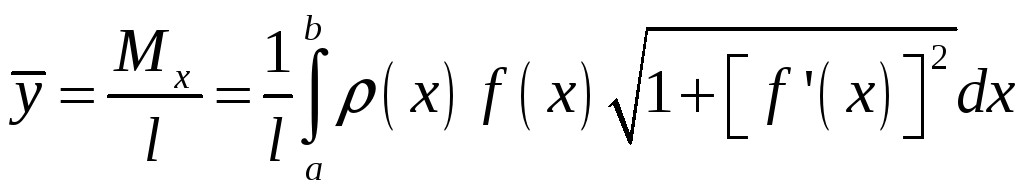 ,
,
где
 - масса дуги.
- масса дуги.
Теорема Гульдена.
Площадь поверхности, образованной вращением дуги плоской кривой вокруг оси, лежащей в плоскости дуги и ее не пересекающей, равна произведению длины дуги на длину окружности, описываемой ее центром масс.
5.2. Физические задачи
С помощью определенного интеграла вычисляются:
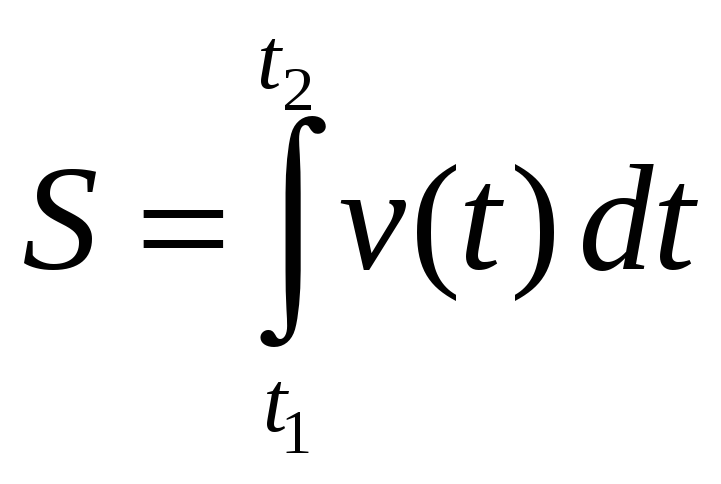 -
путь, пройденный телом, если известен
закон его движения;
-
путь, пройденный телом, если известен
закон его движения;
 -
работа переменной силы, совершаемая в
различных процессах;
-
работа переменной силы, совершаемая в
различных процессах;
 -
давление на погруженную в жидкость с
удельным весом
-
давление на погруженную в жидкость с
удельным весом
![]() вертикальную стенку, ограниченную
кривой
вертикальную стенку, ограниченную
кривой
![]() ;
;
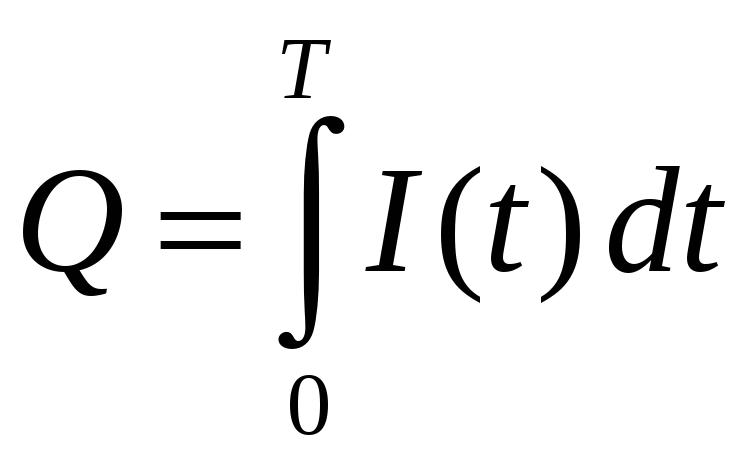 -
количество электричества, протекающее
через сечение проводника при силе тока
-
количество электричества, протекающее
через сечение проводника при силе тока
![]() за время
за время
![]() ;
;
 -
количество тепла, выделяющееся в
проводнике с сопротивлением
-
количество тепла, выделяющееся в
проводнике с сопротивлением
![]() ,
через который протекает ток
,
через который протекает ток
![]() .
.
кинетическая энергия; величина действующей силы; время; объем и др.
|
ПП 22. Геометрические приложения определенного интеграла 1. Вычисление площадей плоских фигур 1.2. Вычисление площадей фигур, заданных в прямоугольных координатах |
||
|
№ п/п |
Задача |
Ответ |
|
ПП 22 №1 |
Вычислите площадь фигуры, ограниченной параболой у = х2, прямыми х = -1 и х = 2 и осью абсцисс . Решение:
S
=
|
3 |
|
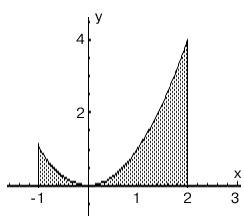
ПП 22 №2 |
Вычислите площадь сегмента, отсекаемого прямой у = -х от параболы у = 2х х2. Решение: Преобразуем уравнение параболы: у = 2х х2 = (х2 2х + 1) + 1, (у 1) = (х 1) 2. Находим
абсциссы точек пересечения параболы
и прямой
S |
|
|
ПП 22 №3 |
Вычислите
площадь эллипса
Решение:
|
|
|
ПП 22 №4 |
Вычислите площадь фигуры, ограниченной графиками функций: х = 4 (у 1)2 и х = у2 4у + 3. Р Найдем точки пересечения графиков функций х = 4 (у 1)2 и х = у2 4у + 3: 4 (у 1)2 = у2 4у + 3 2у (у 3) = 0 у = 0; 3.
|
9 |
|
1.2. Вычисление площадей фигур, заданных кривыми в параметрическом виде |
||||||||||||||||||||
|
№ п/п |
Задача |
Ответ |
||||||||||||||||||
|
ПП 22 №5 |
Вычислите площадь эллипса. Решение: Уравнения эллипса в параметрической форме имеют вид:
|
|
||||||||||||||||||
|
ПП 22 №6 |
Найдите площадь фигуры, ограниченной первой аркой циклоиды х = а (t sin t); у = а (1 cos t) и отрезком оси абсцисс Решение:
Точкам
О и
А
соответствуют значения параметра tО
= 0 и tА
= 2,
искомая площадь равна
S=
= =а2
|
3a2 |
||||||||||||||||||
|
ПП 22 №7 |
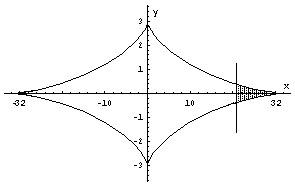
Вычислите площадь фигуры, ограниченной линиями, заданными
уравнениями х
=
РЕШЕНИЕ: Найдем точки пересечения астроиды
cos
t
=
|
|
||||||||||||||||||
|
ПП 22 №8 |
Вычислите площадь фигуры, ограниченной линиями
РЕШЕНИЕ:
Точки пересечения линий: 2
2сos
t
= 3; сos
t
=
t
a
= x
Площадь заштрихованной области: S= = = =
= =
= =
4
4
|
5,196152 |
||||||||||||||||||
|
1.3. Площадь фигур, заданных в полярной системе координат |
||||||||||||||||||
|
№ п/п |
Задача |
Ответ |
||||||||||||||||
|
ПП 22 №9 |
В Решение: В силу симметрии достаточно вычислить половину искомой площади.
|
|
||||||||||||||||
|
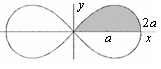
ПП 22 №10 |
Найдите площадь, заключённую внутри лемнискаты Бернулли 2 = а2 сos2 . Р В силу симметрии достаточно вычислить одну четверть искомой площади:
|
а2 |
||||||||||||||||
|
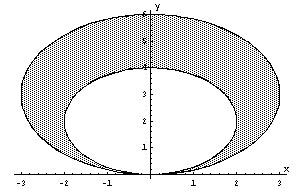
ПП 22 №11 |
Вычислите площадь фигуры, ограниченной линиями, заданными уравнениями в полярных координатах r = 6 sin , r = 4 sin . Р Линии в полярных координатах r = 6 sin и r = 4 sin представляют собой окружности, смещенные вверх по оси Оy, с радиусами 3 и 2 соответственно. S
=
Площадь фигуры, заключенной между окружностями:
S
= S1
S2
= = = |
15,708 |
||||||||||||||||
|
ПП 22 №12 |
Вычислите площадь фигуры, ограниченной линиями 1 = cos
2
=
РЕШЕНИЕ: 1:
2
=
-
окружность с центром в точке О1
и
радиусом R1
=
2
=
(получается
поворотом
= cos
на
и
увеличением радиуса в
Площадь заштрихованной фигуры: S
=
=
= = = |
0,535598 |
||||||||||||||||
|
ПП 22 №13 |
Вычислите площадь фигуры, ограниченной линией
РЕШЕНИЕ:
сos
S
= |
6,212389 |
||||||||||||||||
|
ПП 22 №14 |
Вычислите площадь фигуры, ограниченной линиями 1 = 4 sin 3, 2 = 2 ( 2). РЕШЕНИЕ: sin 3 0 2n 3 + 2n, n z,
На интервале (0, 2) укладывается три периода функции sin 3. Составим
таблицу для
Найдем
угол ,
соответствующий точке пересечения
линий
4sin
3
= 2; sin
3
=
Половина площади одной "луночки":
Sл
=
=
= Площадь всех заштрихованных областей: S
= 6 Sл
=
|
7,652892 |
||||||||||||||||
|
ПП 22. Геометрические приложения определенного интеграла 2. Вычисление длины дуги кривой 2.1. Длина плоской кривой в прямоугольных координатах
|
||
|
№ п/п |
Задача |
Ответ |
|
ПП 22 №15 |
Вычислите
длину кривой
Решение:
|
|
|
ПП 22 №16 |
Вычислите длину дуги кривой, заданной в прямоугольной системе координат уравнением у
=
РЕШЕНИЕ: у
l
=
|
|
|
2.2. Длина плоской и пространственной кривой, заданной в параметрическом виде |
||
|
№ п/п |
Задача |
Ответ |
|
ПП 22 №17 |
Вычислите длину винтовой линии
Решение:
|
|
|
ПП 22 №18 |
Вычислите длину дуги кривой, заданной параметрическими уравнениями:
0 t . l
=
l
=
|
|
|
2.2. Длина кривой, заданной в полярных координатах |
||
|
№ п/п |
Задача |
Ответ |
|
ПП 22 №19 |
Вычислите
длину окружности Решение:
|
|
|
ПП 22 №20 |
В l
=
Линия представляет собой часть дуги окружности, с центром в точке (0; 3) и радиусом, равным 3. l
=
|
6,28319 |
|
ПП 22. Геометрические приложения определенного интеграла 3. Площадь поверхности вращения |
||
|
№ п/п |
Задача |
Ответ |
|
ПП 22 №21 |
Найдите площадь поверхности, образованной вращением астроиды х2/3 + у2/3 = а2/3 вокруг оси Ох. Решение: у = (а2/3 х2/3)3/2, у
=
Qх
= 22
= |
|
|
ПП 22 №22 |
Найдите площадь поверхности, образованной вращением одной арки циклоиды х = а (t sin t), у = а (1 cos t) вокруг оси Ох. Решение: х = а (1 cos t), у = а (sin t),
=
а
Qх
= 2
=8а2 =
16а2
|
|
|
ПП 22 №23 |
Найдите площадь поверхности, образованной вращением кардиоиды = 2а (1+ cos) вокруг полярной оси. Решение: = 2а sin ,
Qх
=2 =
64 а2
|
|
|
ПП 22. Геометрические приложения определенного интеграла 4. Вычисление объемов тел 4.1. Вычисление объемов по заданным площадям поперечных сечений |
|||
|
№ п/п |
Задача |
Ответ |
|
|
ПП 22 №24 |
Найдите объём тела, основанием которого является круг с радиусом а, а сечение плоскостью, перпендикулярной фиксированному диаметру круга, представляет собой равнобедренный треугольник высотой h. Решение:
Выберем
систему координат, начало которой
совпадает с центром круга. Сечение тела плоскостью, перпендикулярной оси Ох,
-
равнобедренный треугольник с основанием
2у
= 2
S(х)
=
V
=
|
|
|
|
ПП 22 №25 |
Найдите
объем эллипсоида
Решение:
|
|
|
|
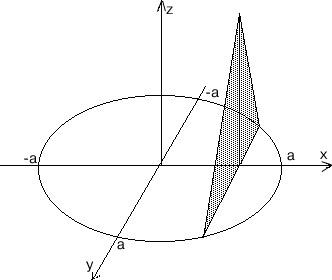
ПП 22 №26 |
Вычислите объем тела, ограниченного поверхностями
Первая поверхность представляет собой эллипсоид с полуосями 4, 13, 14 соответственно, вторая и третья поверхности – плоскости, параллельные координатной плоскости Оxy.
S
=
Найдем S (z)
V
=
|
241,903 |
|
|
4.2. Вычисление объемов тел вращения |
|||
|
ПП 22 №27 |
Найдите объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной кривой у2 = (х 1)3 и прямой х = 2 Решение: Vх
=
|
|
|
|
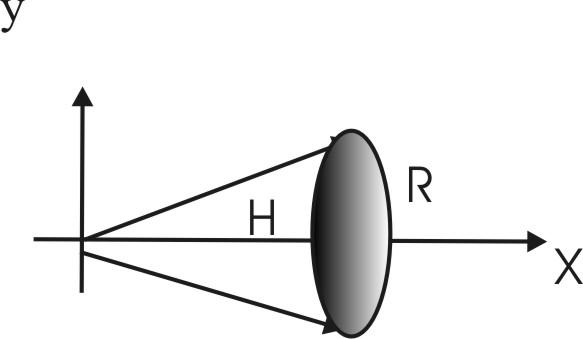
ПП 22 №28 |
Найдите объем конуса с высотой Н и радиусом основания R. Решение:
|
|
|
|
ПП 22№29 |
Вычислите объем тела, образованного вращением вокруг оси Оy фигуры, ограниченной графиками функций
РЕШЕНИЕ: Перепишем уравнения линий в виде
V
=
V
=
=
=
=
=
|
0,896602 |
|
|
ПП 22. Геометрические приложения определенного интеграла 5. Приложеия определенного интеграла к решению некоторых задач механики и физики 5.1. Моменты и центры масс плоских кривых |
||
|
№ п/п |
Задача |
Ответ |
|
ПП 22 №30 |
Найдите координаты центра масс дуги окружности
0
t
/2,
РЕШЕНИЕ:
l
=
|
( |
|
ПП 22 №31 |
Найдите координаты центра масс полуокружности
РЕШЕНИЕ: Вследствие
симметрии
По теореме Гульдена имеем
Отсюда
|
|
|
5.2. Физические задачи |
||
|
ПП 22 №32 |
Скорость
прямолинейного движения тела выражается
формулой
РЕШЕНИЕ:
|
150 м |
|
ПП 22 №33 |
Какую работу необходимо затратить для того, чтобы тело массы поднять с поверхности Земли, радиус которой R, на высоту h? Чему равна работа, если тело удаляется в бесконечность? РЕШЕНИЕ: Работа
переменной силы
Закон
Ньютона:
На
поверхности r=R,
F=mg,
mg=k
При
|
|
|
ПП 22 №34 |
С
какой силой жидкость плотности
РЕШЕНИЕ: По
закону Паскаля сила Р,
с которой жидкость плотности
Р Из подобия треугольников CAB и CDE:
Сила давления жидкости на всю пластинку равна:
|
|
|
ПП 22 №35 |
Два
электрических заряда
а) удалится на расстояние 30 см; б) удалится в бесконечность? РЕШЕНИЕ: Закон
Кулона:
а)
б)
|
|
|
ПП 22 №36 |
Найти
давление бензина, находящегося в
цилиндрическом баке высотой
РЕШЕНИЕ: Элемент
давления на поверхность стенки в
выделенной полоске выразится так:
|
|
|
ПП 22 №37 |
Какую работу нужно совершить, чтобы растянуть пружину на 4 см, если известно, что от нагрузки в 1 Н она растягивается на 1 см? РЕШЕНИЕ: По
закону Гука растягивающая сила
|
|
|
ПП 22 №38 |
Определить
работу, необходимую для запуска ракеты
для запуска ракеты весом
РЕШЕНИЕ: Сила
|
|
|
ПП 22 №39 |
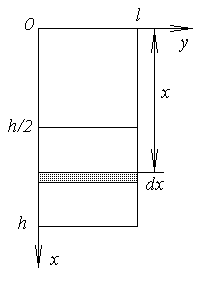
Прямоугольный сосуд наполнен равными по объему частями воды и масла, причем масло вдвое легче воды. Показать, что сила давления на каждую стенку сосуда уменьшится на одну пятую, если вместо смеси взять одно масло. РЕШЕНИЕ: У |
|

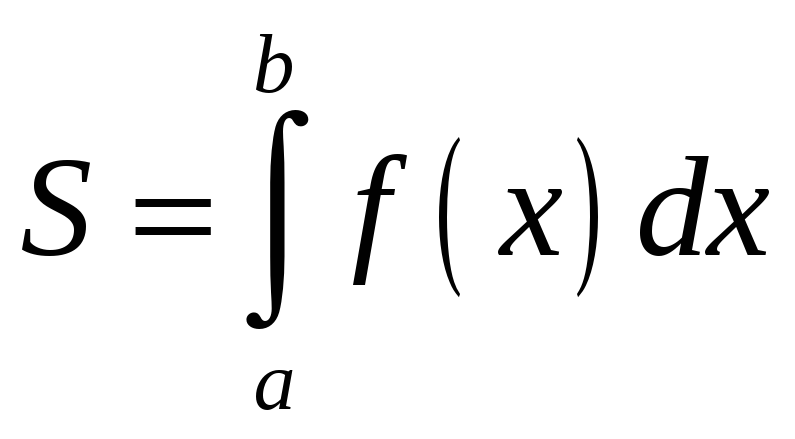 .
.
 .
.
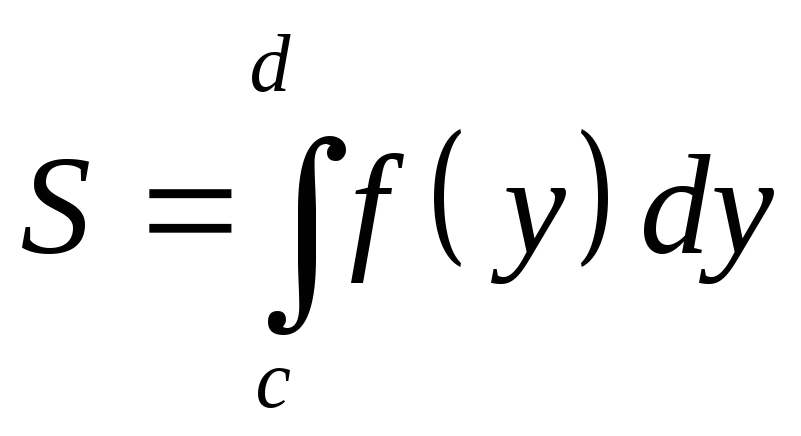 .
.


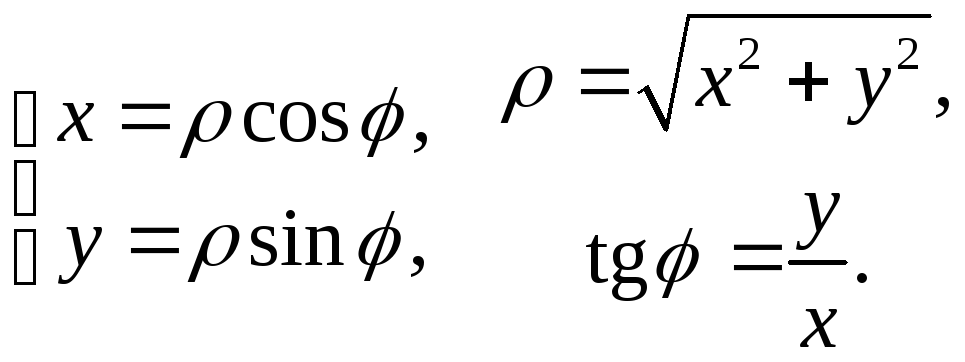
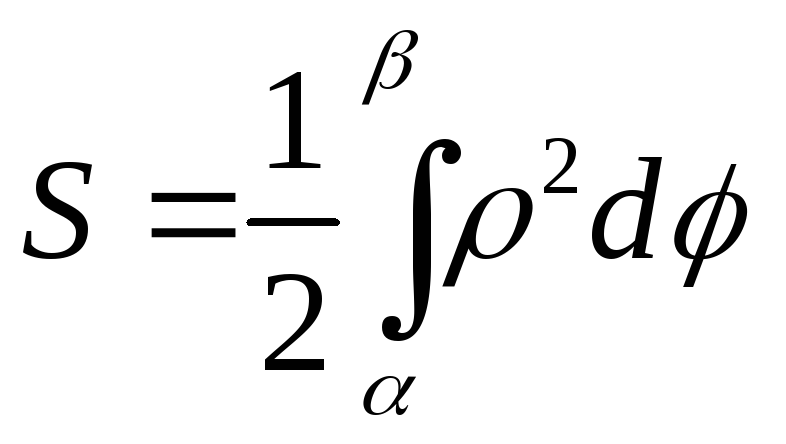 -
площадь криволинейного сектора.
-
площадь криволинейного сектора.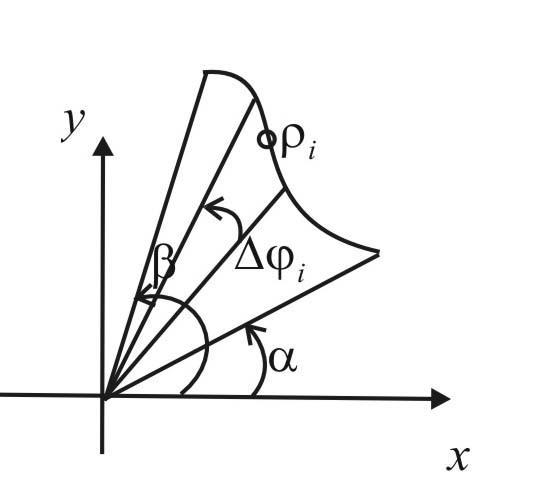
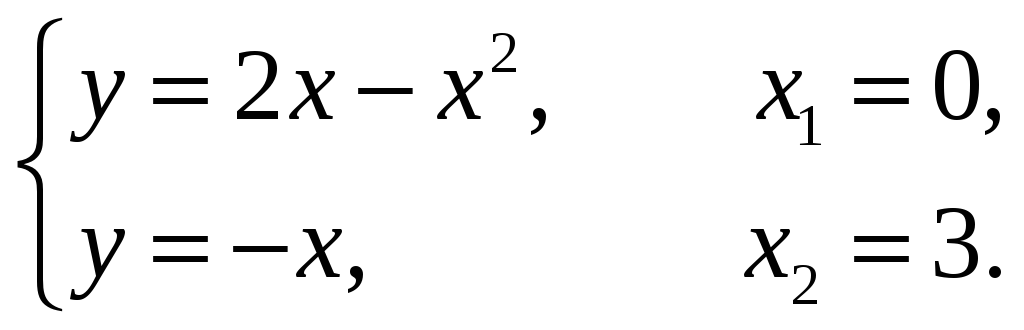 (0,0)
и (3,-3)
(0,0)
и (3,-3)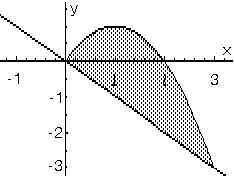 =
=
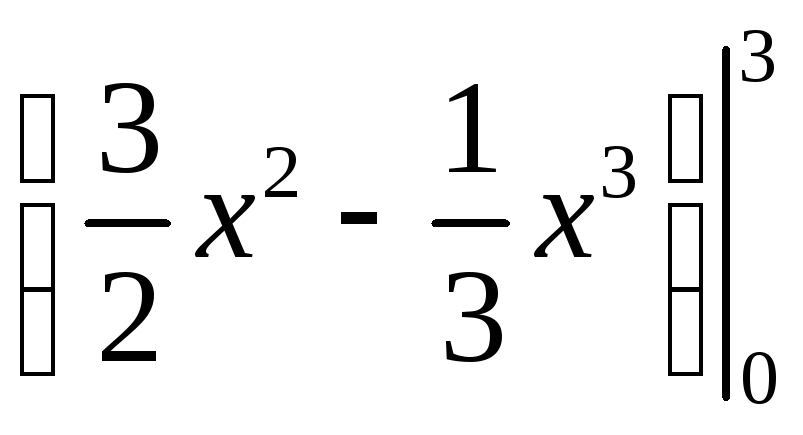 =
=
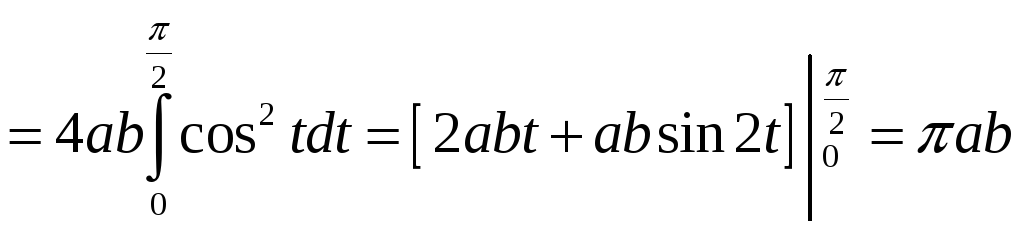 ,
,
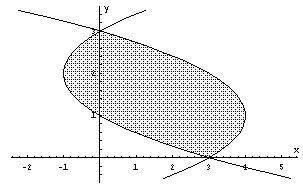 ЕШЕНИЕ:
ЕШЕНИЕ:
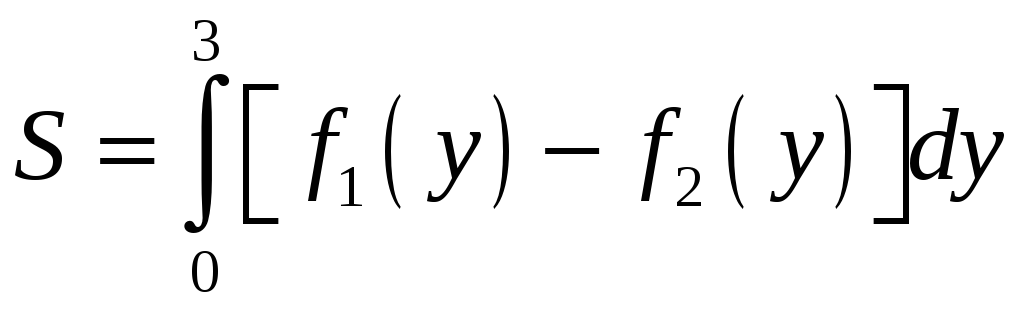
 =
=
=
=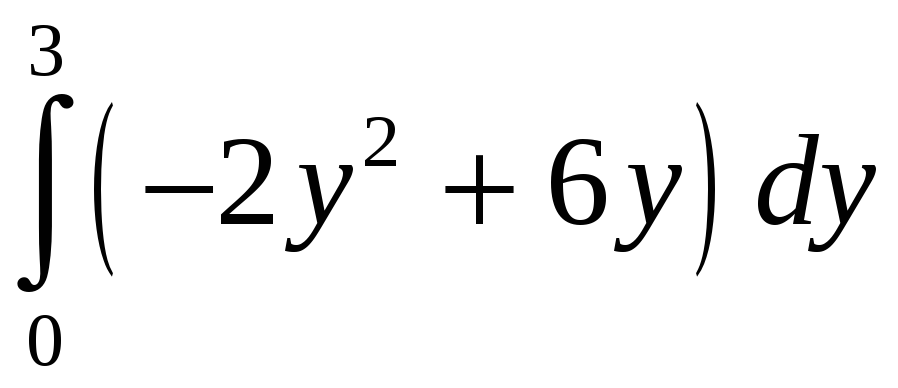 =
= = 9.
= 9.
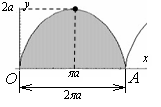
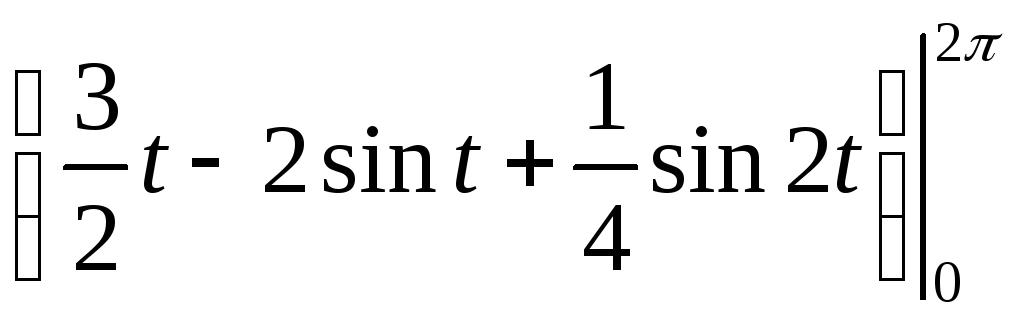 =
3a2.
=
3a2.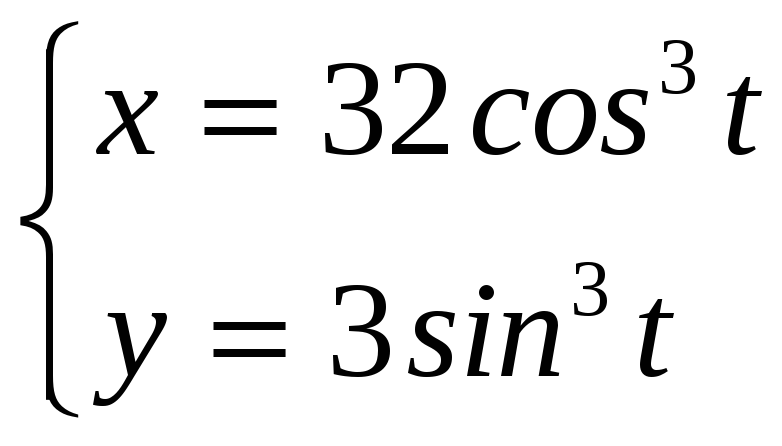 ,
,
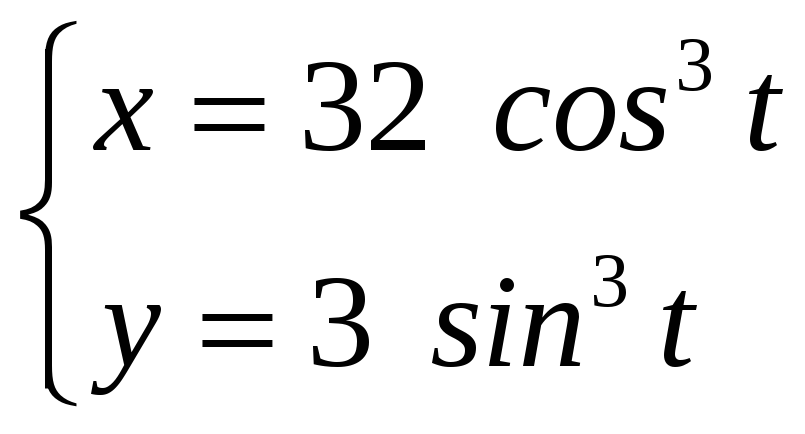 и
прямой х
=
и
прямой х
=
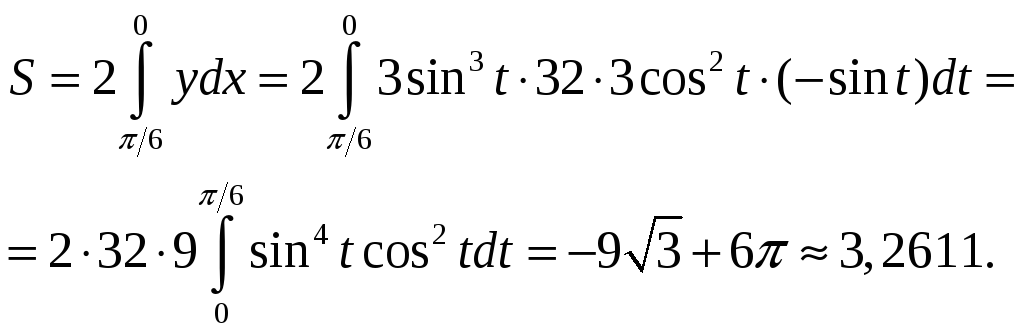


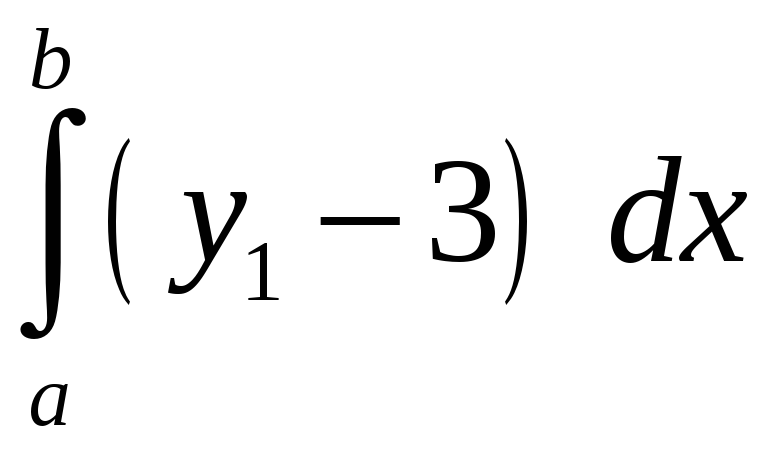 =
=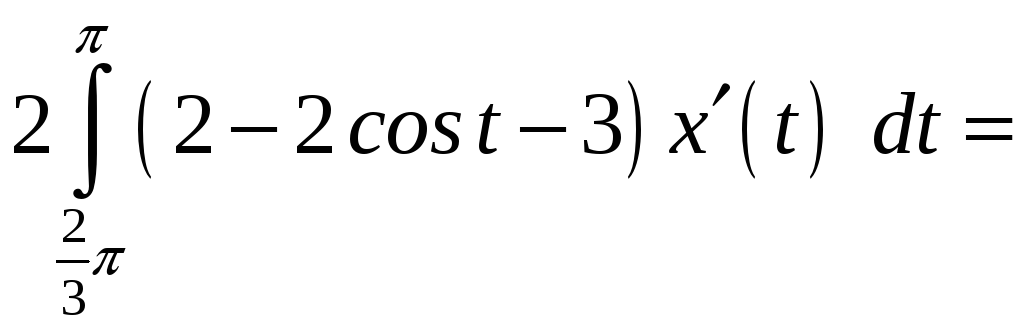
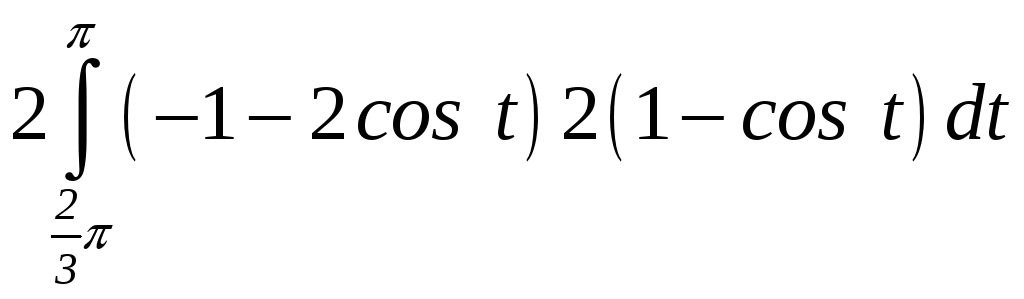 =
=
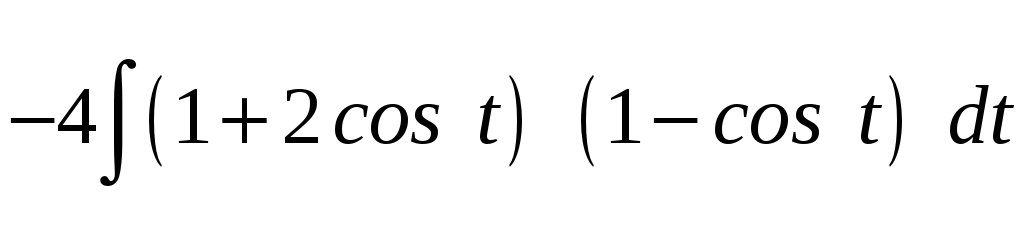 =
=
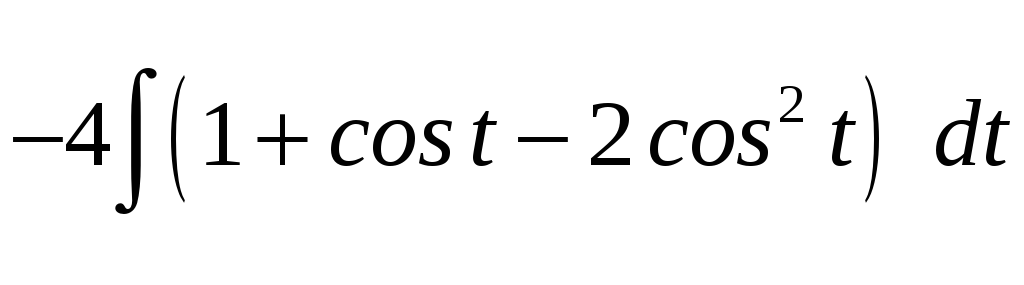 =
=
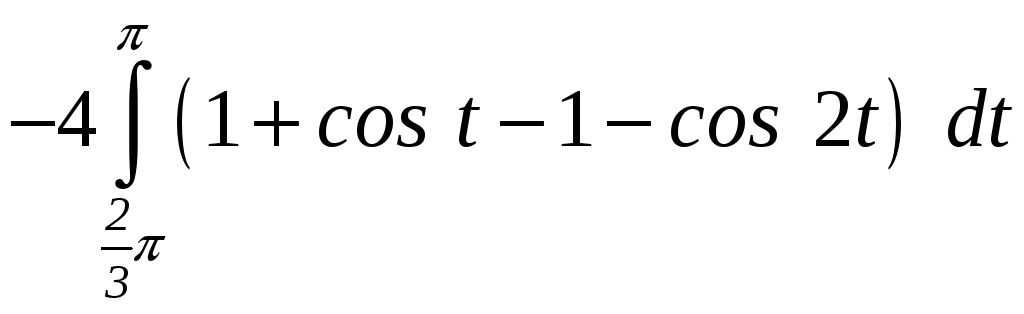 =
=
 =
=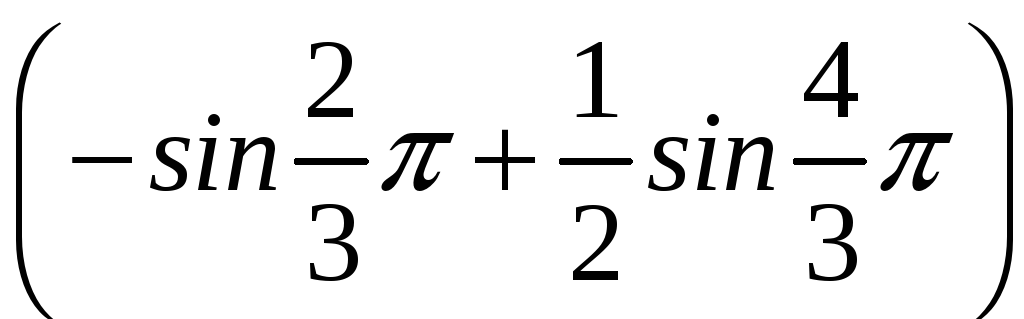 =
=
 = 3
= 3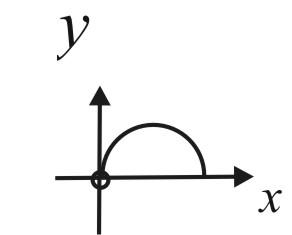 ычислите
площадь круга
ычислите
площадь круга
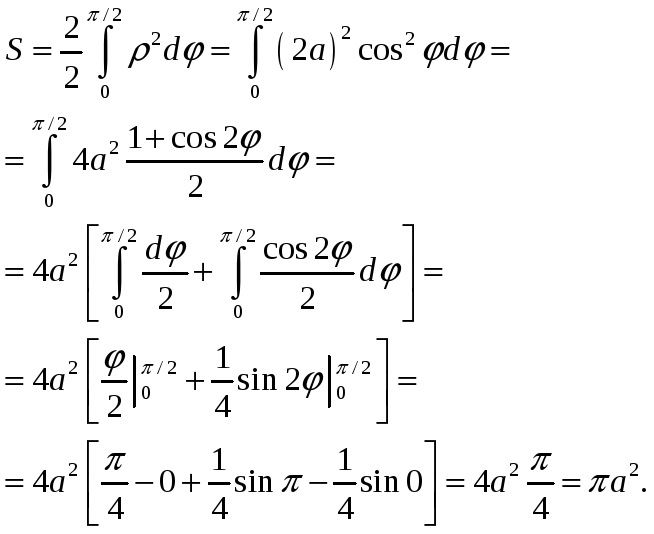
 ешение:
ешение: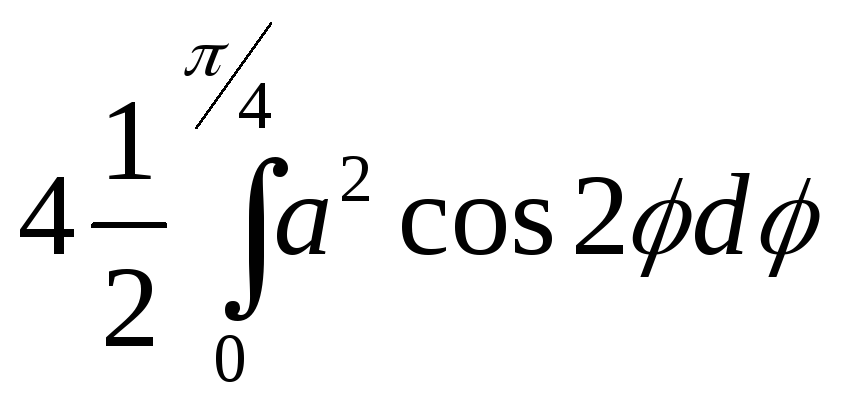 =
=
 ЕШЕНИЕ:
ЕШЕНИЕ: - площадь фигуры, ограниченной линией
=
().
- площадь фигуры, ограниченной линией
=
().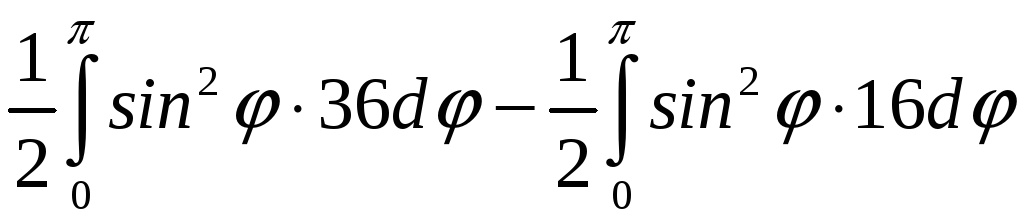 =
=
 ==
==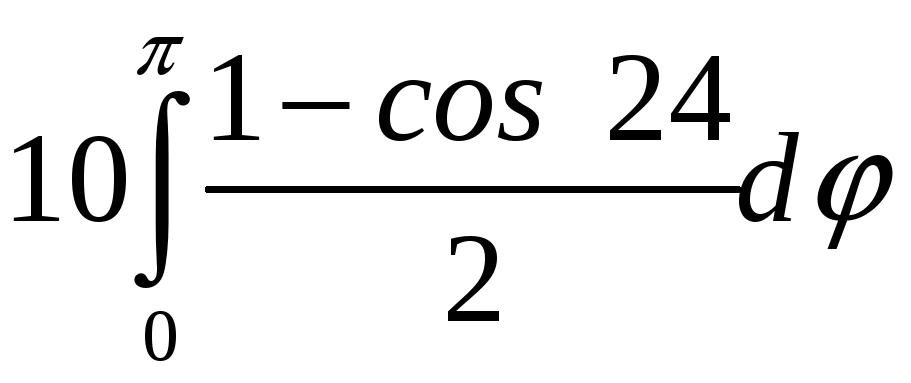 =
=
=
= = 5
15,708.
= 5
15,708.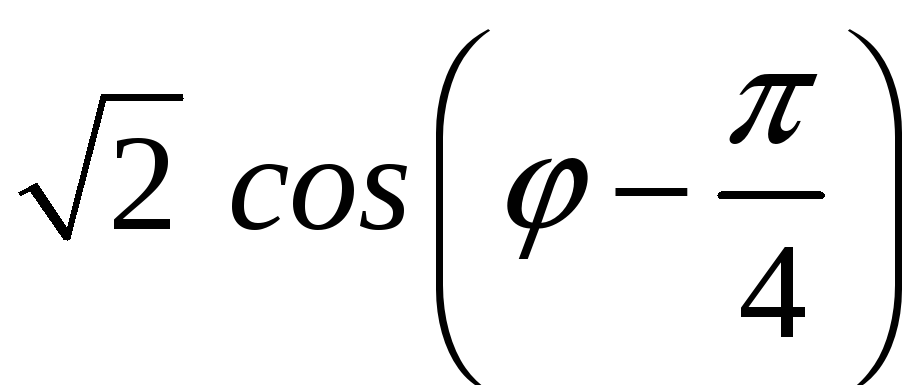 ,
,
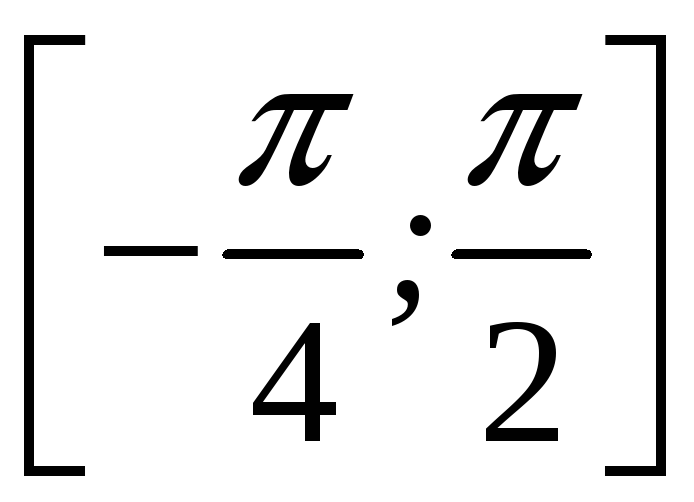 .
.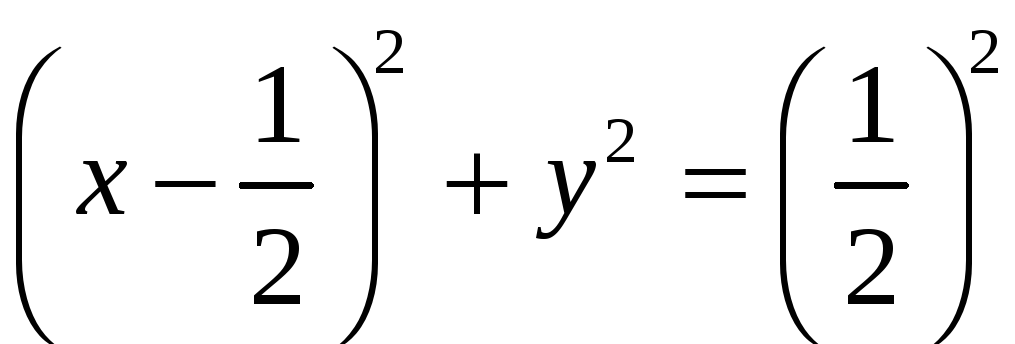
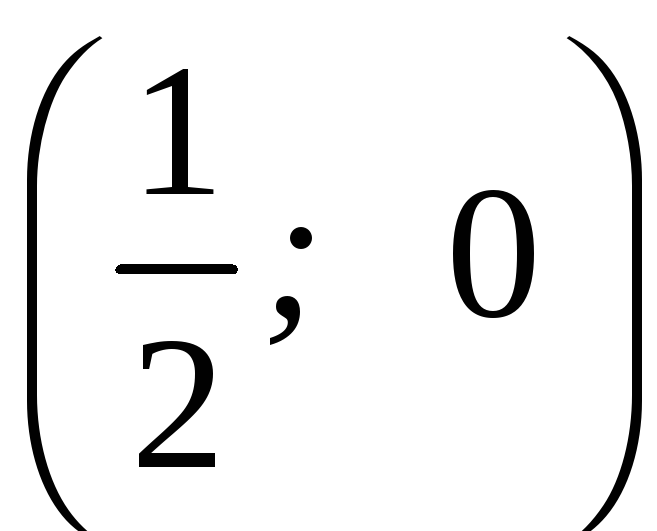
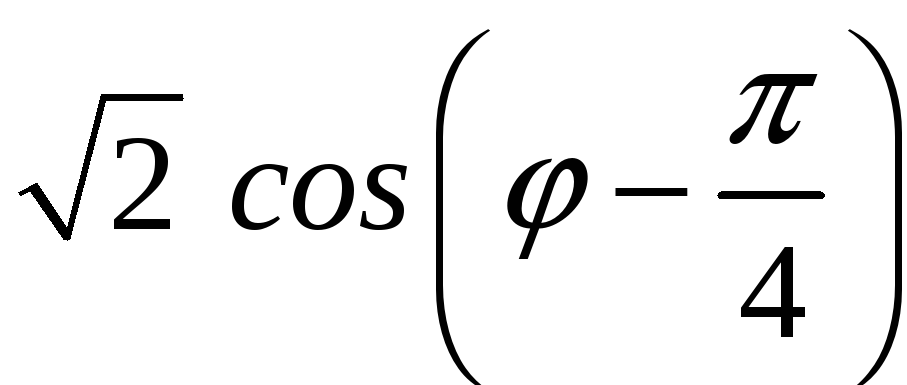 – окружность с радиусом R2
=
– окружность с радиусом R2
=

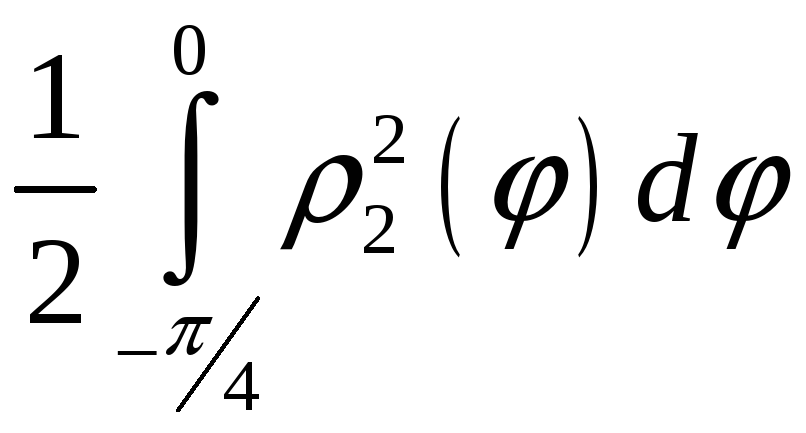 +
+
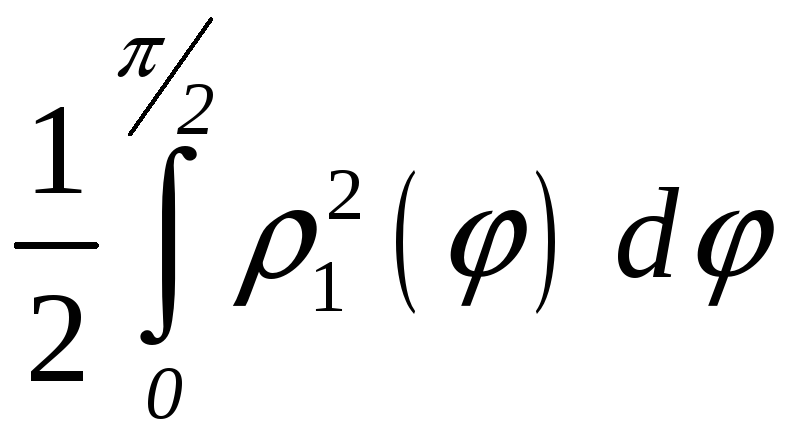 =
=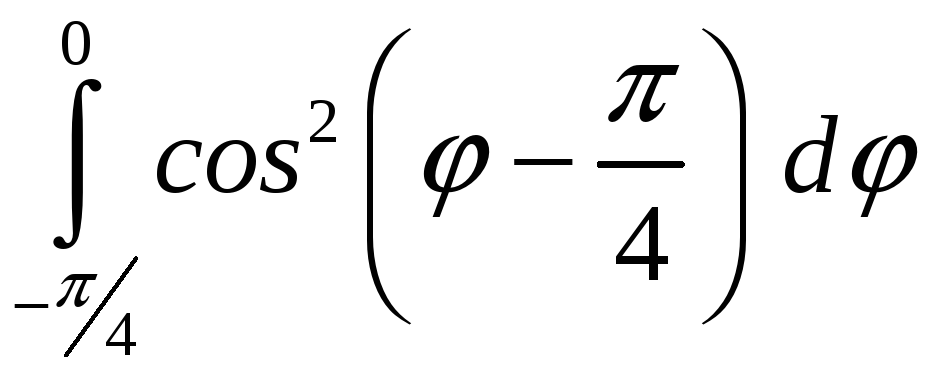 +
+
 =
=
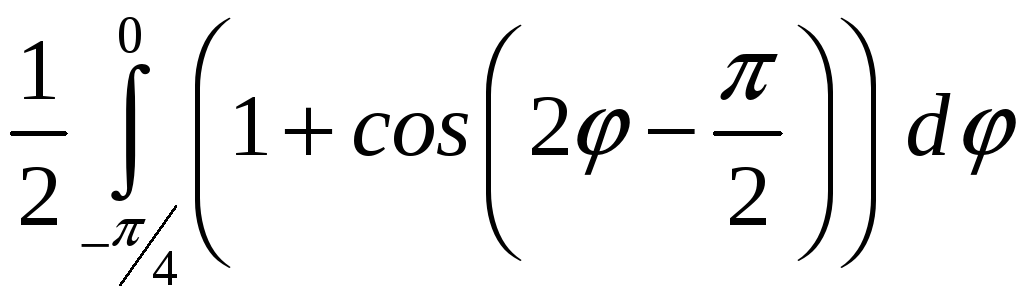 +
+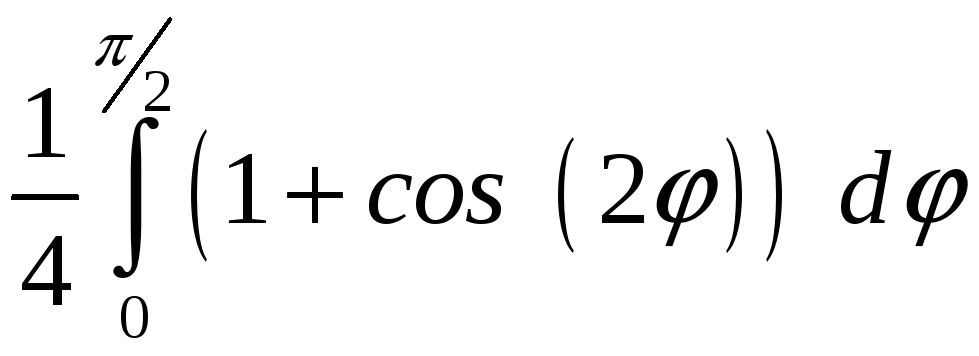 =
=
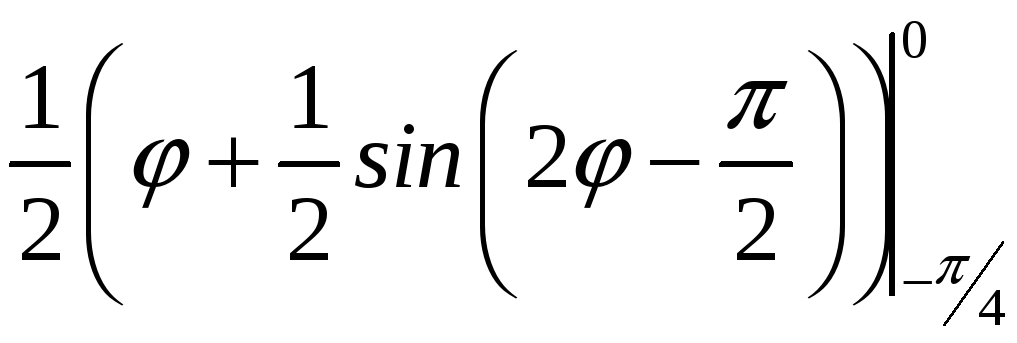 +
+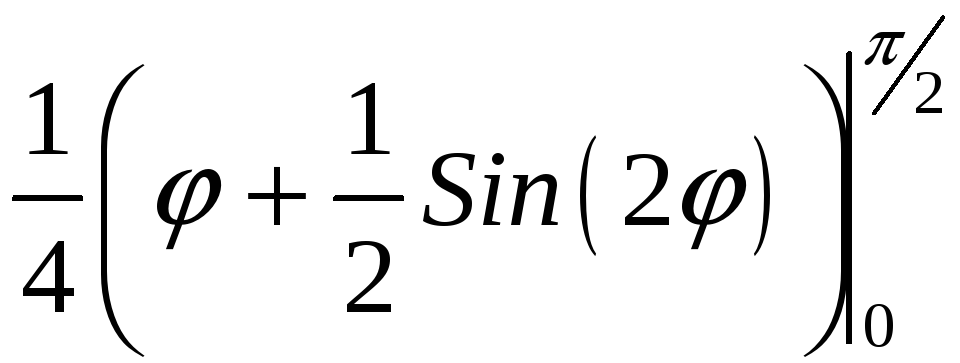 =
=
 +
+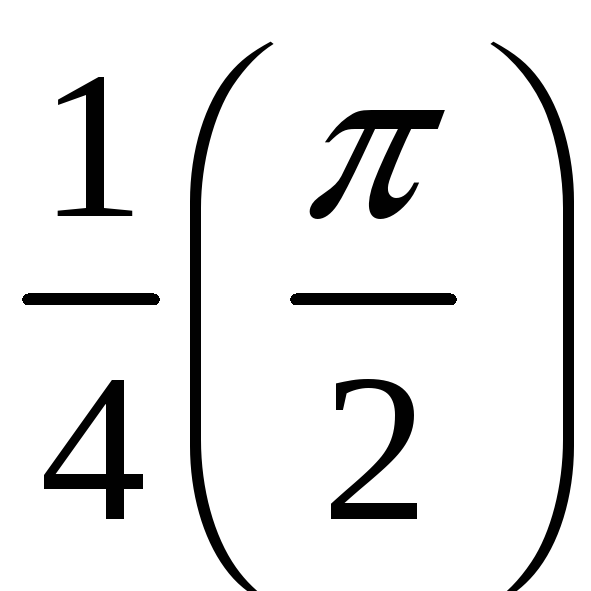 =
=
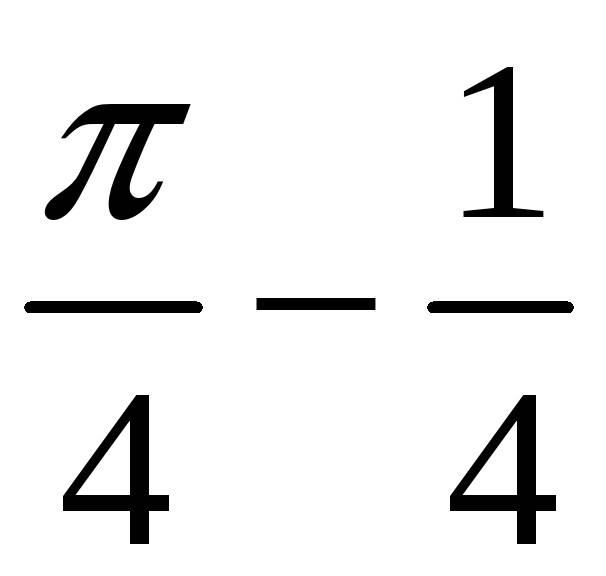 =
=
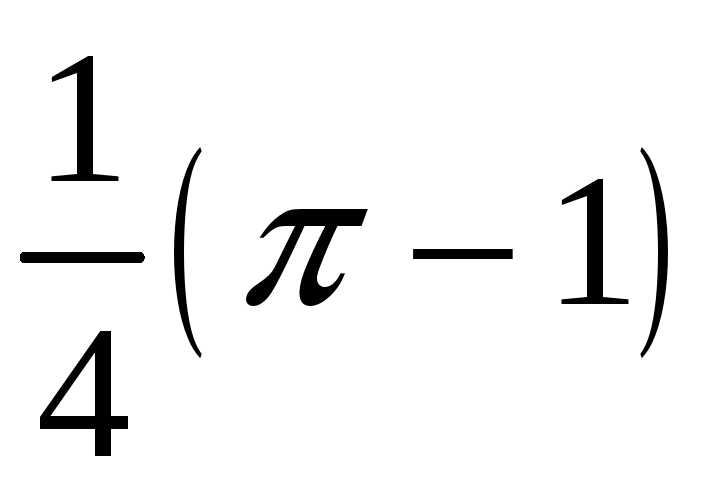
0,535598.
0,535598.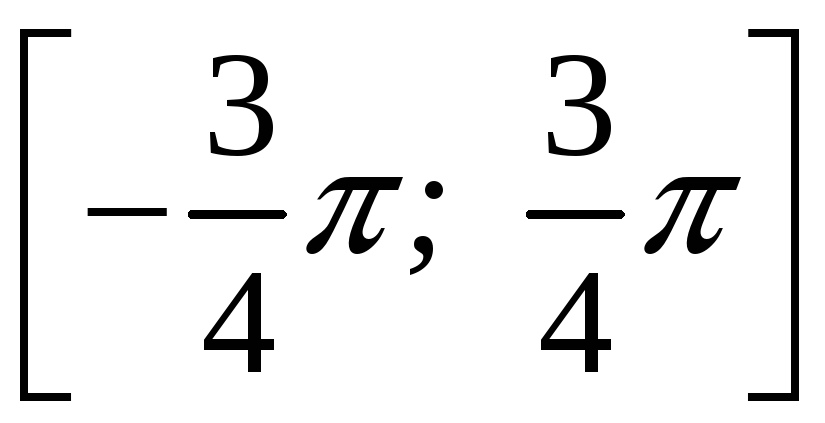 .
сos
- четная
функция, фигура симметрична относительно
оси Ох.
.
сos
- четная
функция, фигура симметрична относительно
оси Ох.
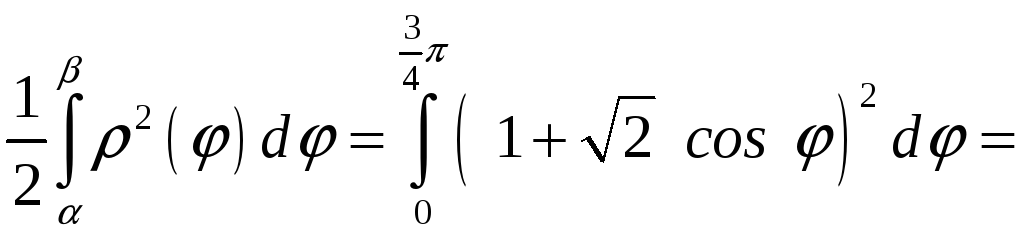 =
= =
=
=
= = =
= = =
=
=
= =
=
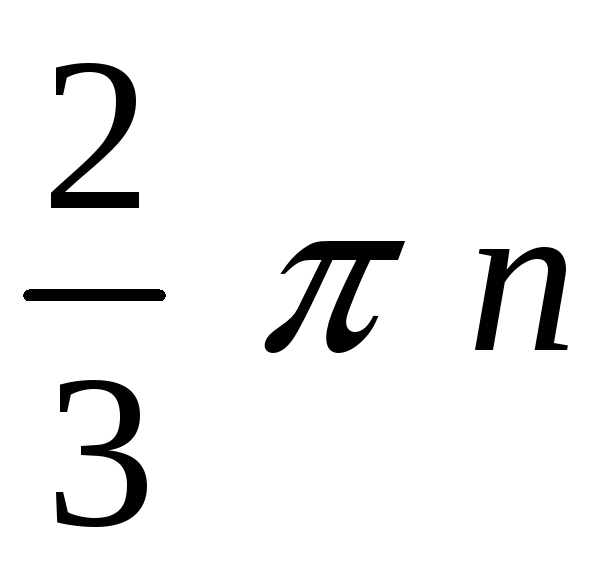
 .
.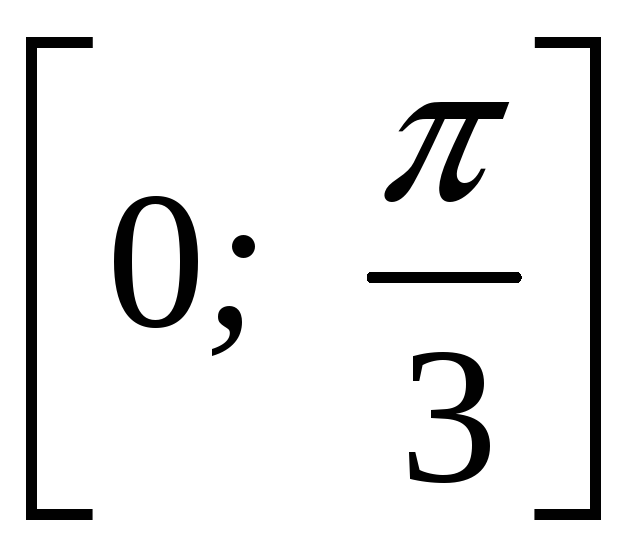 и учтем периодичность:
и учтем периодичность:
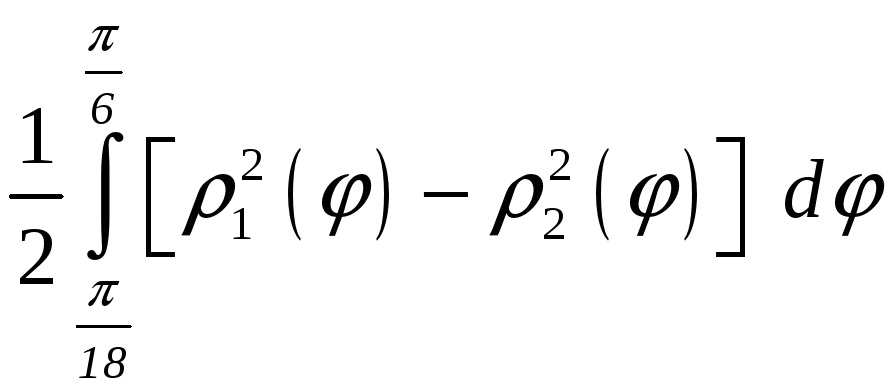 =
=
=
=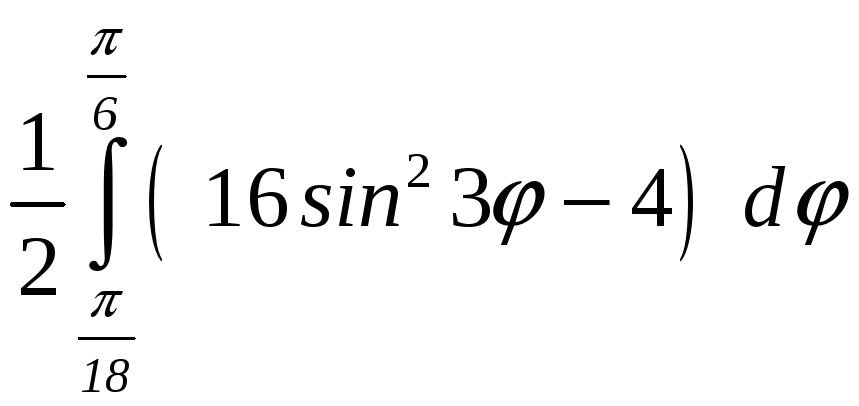 =
=
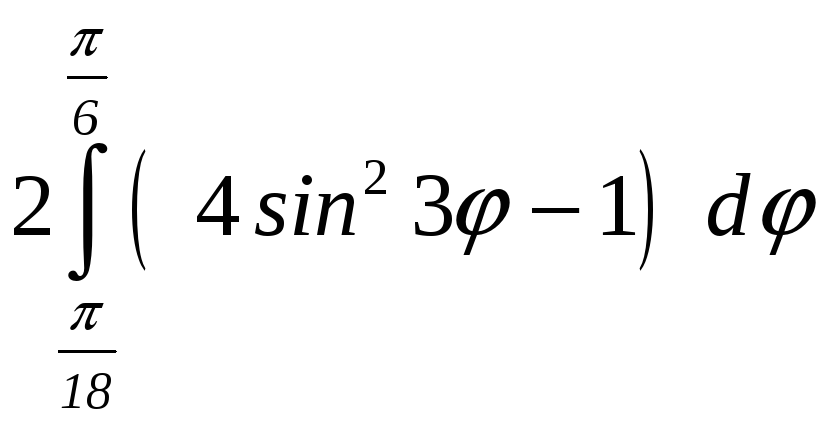 =
= =
=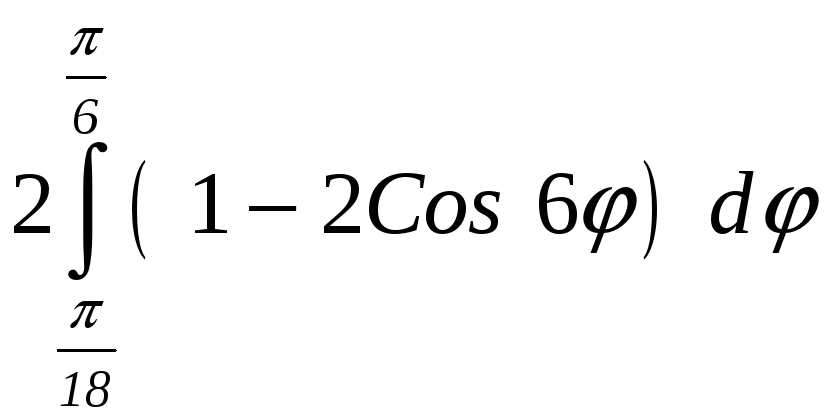 =
= =
=2
=
=2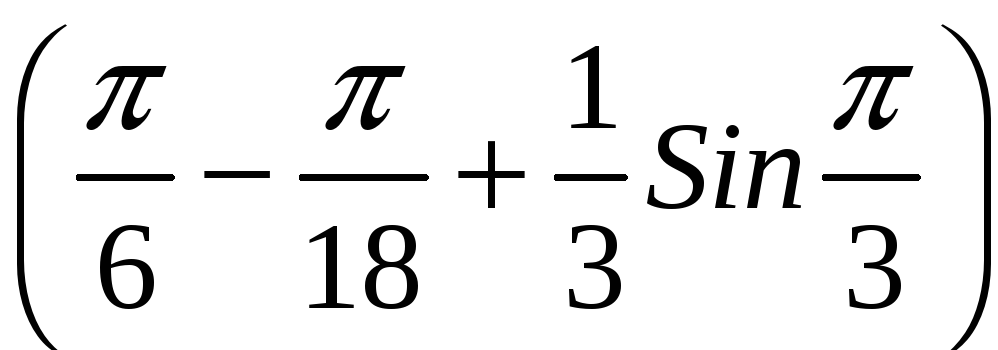 = 2
= 2 ==
==
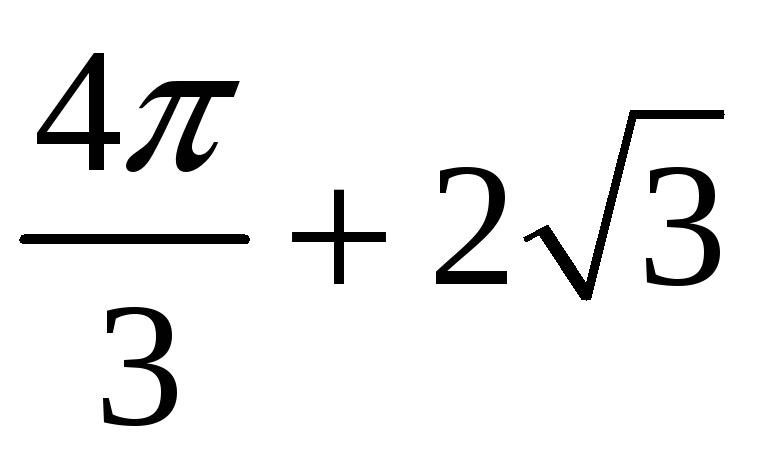
7,652892.
7,652892.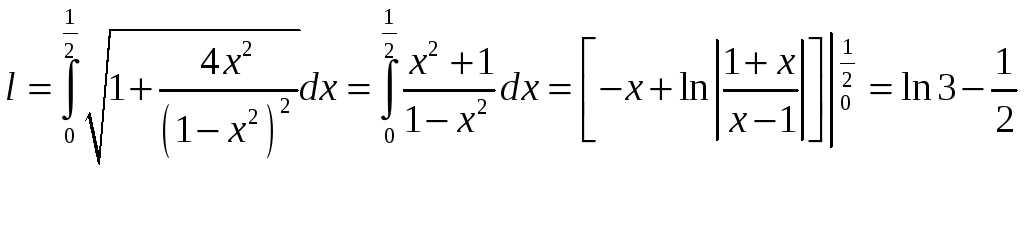
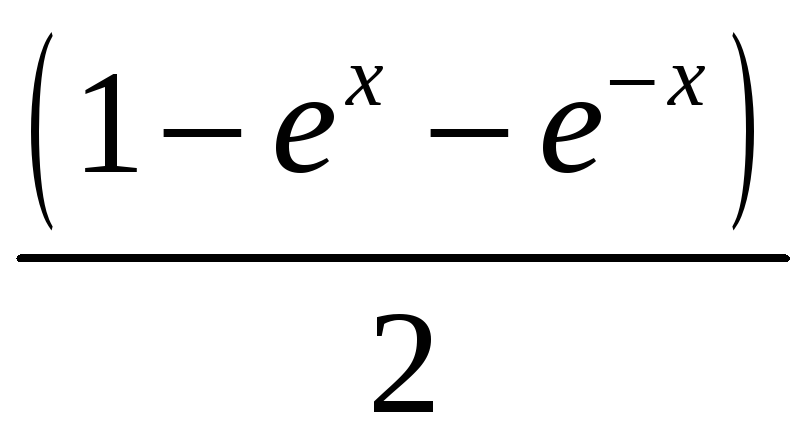 ,
0
х
3.
,
0
х
3. =
=
 =
=
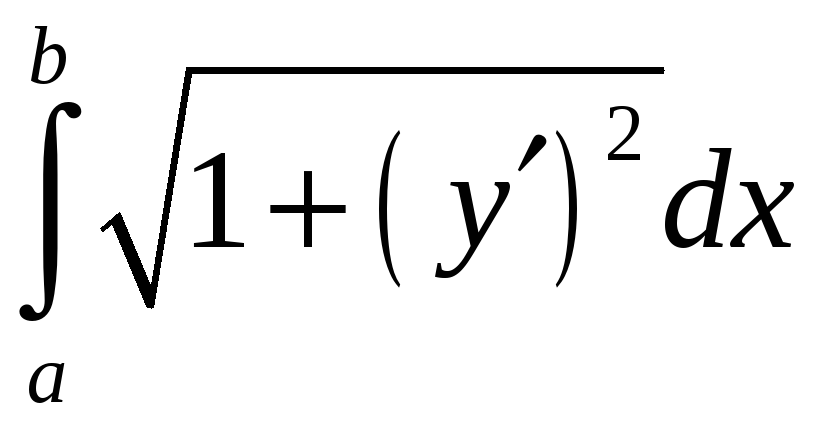 =
=
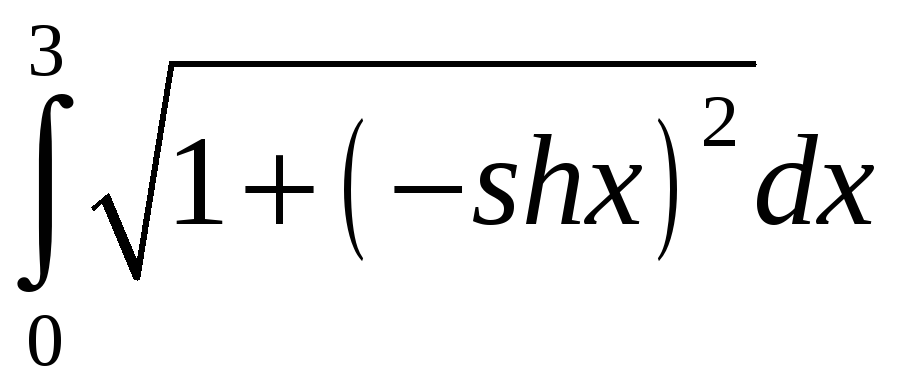 = =
= =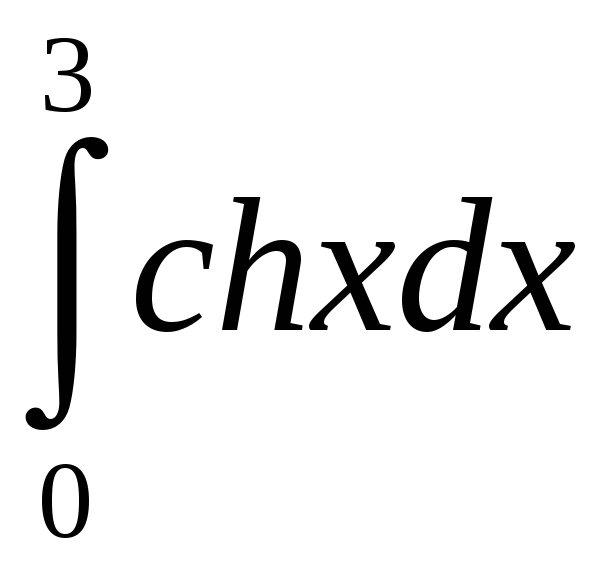 = (т.к. ch2х
sh2х
= 1)=
= (т.к. ch2х
sh2х
= 1)=
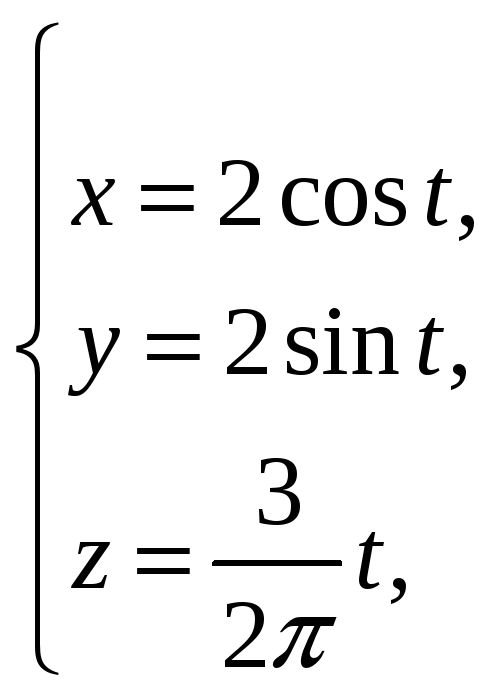
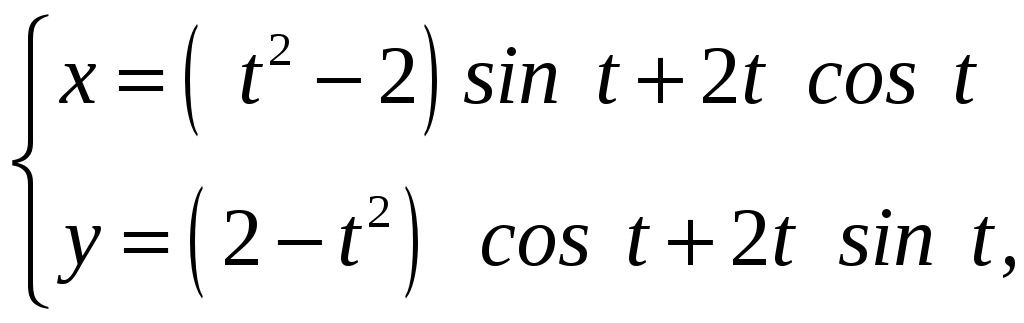
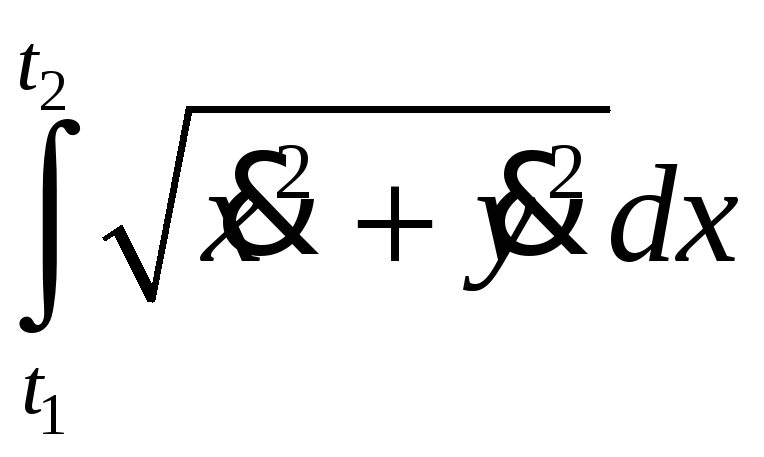 .
.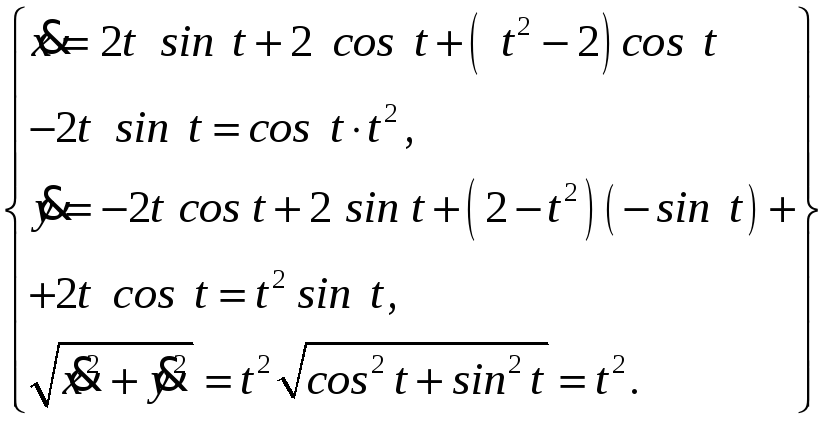
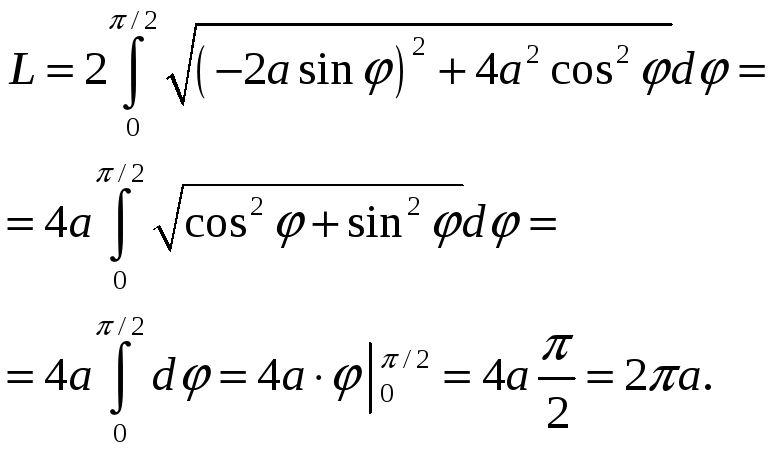
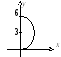 ычислите
длину дуги кривой, заданной уравнением
в полярных координатах
= 6 sin
,
0
ычислите
длину дуги кривой, заданной уравнением
в полярных координатах
= 6 sin
,
0
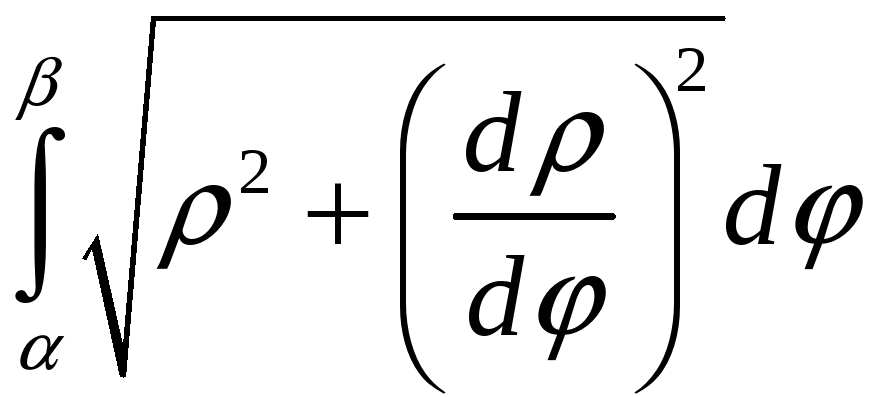 .
. =
=
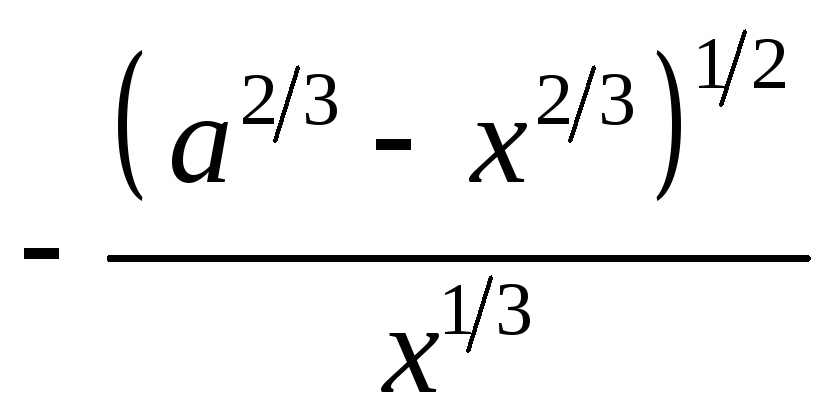 ,
,
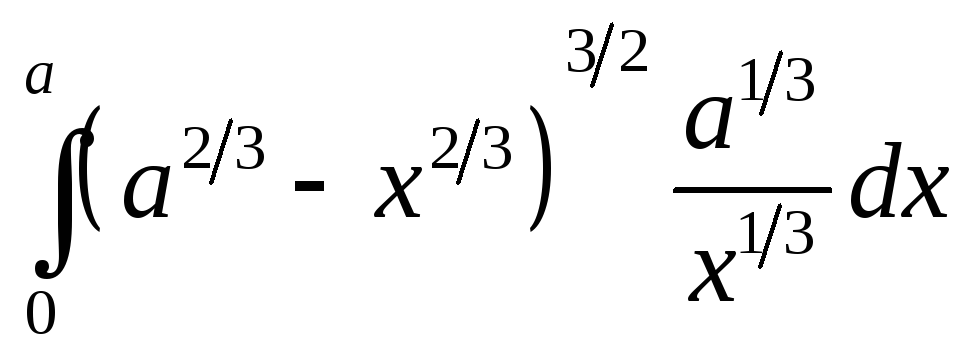 =
=
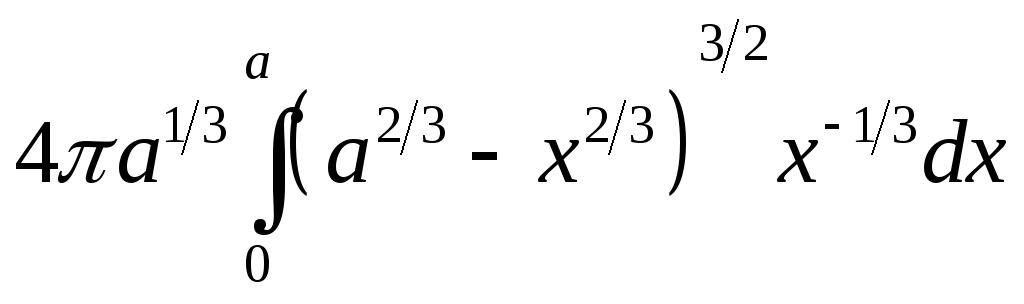 = =4а1/3
= =4а1/3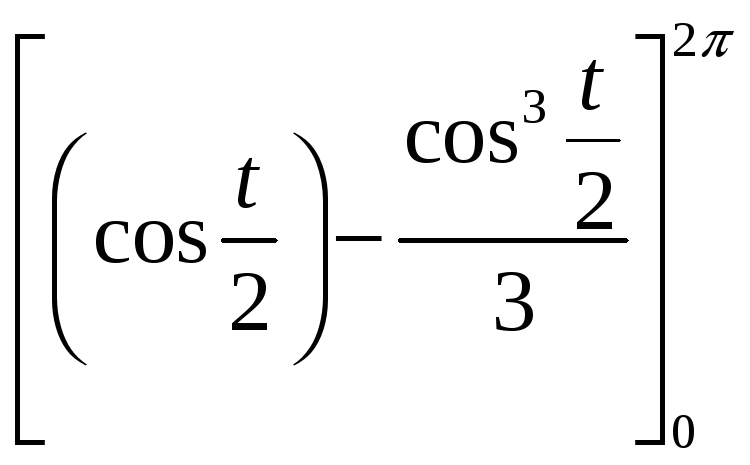 =
=
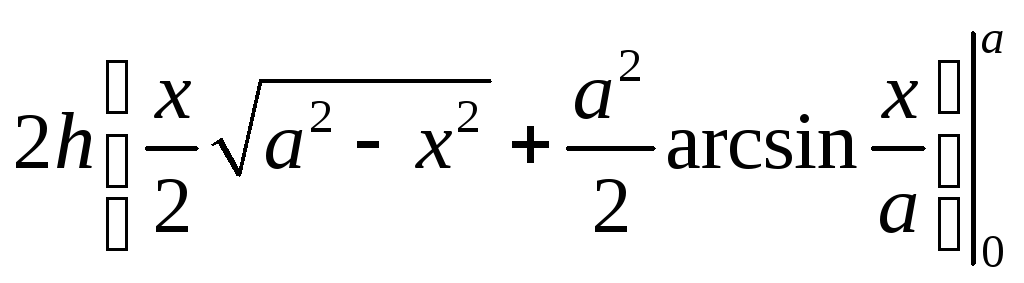 =
=
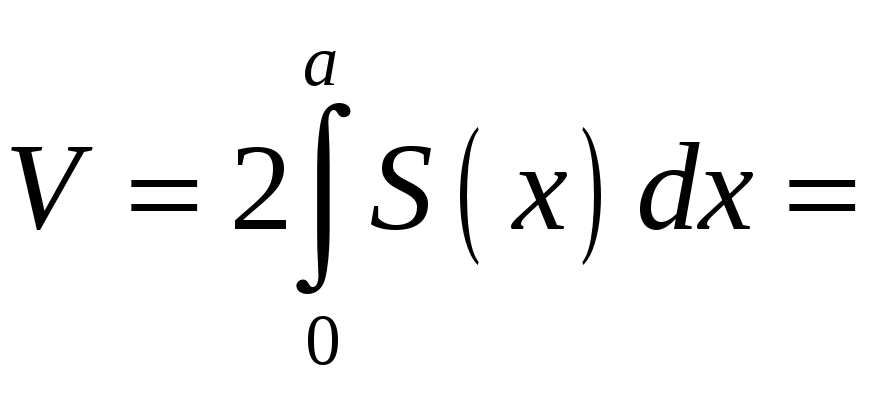

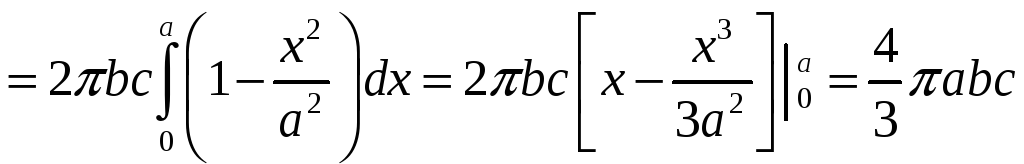 .
. ,
z
= 7, z
= 0.
,
z
= 7, z
= 0.
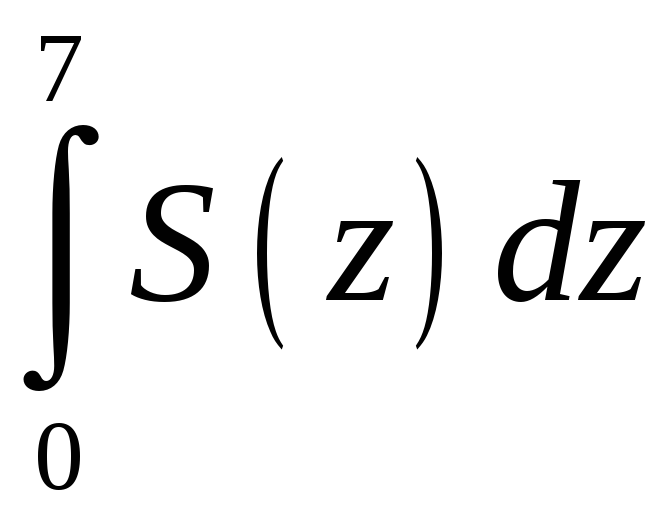 .
.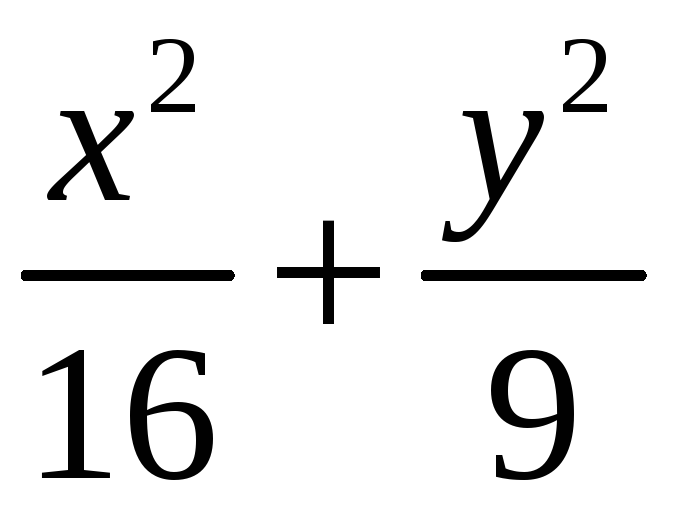 =
1
=
1
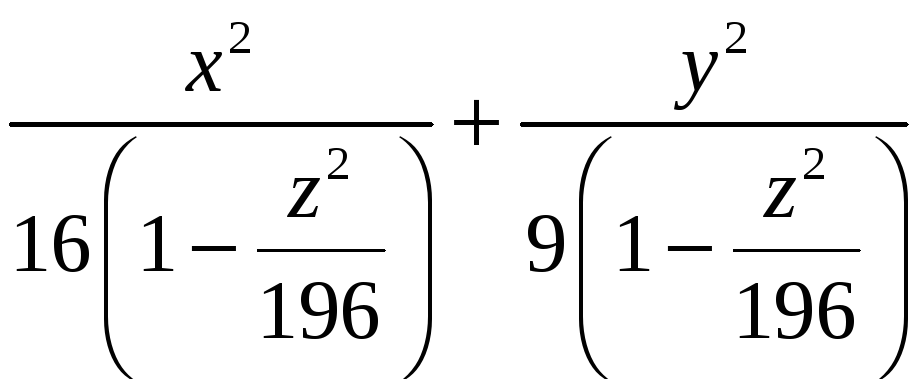 = 1.
= 1.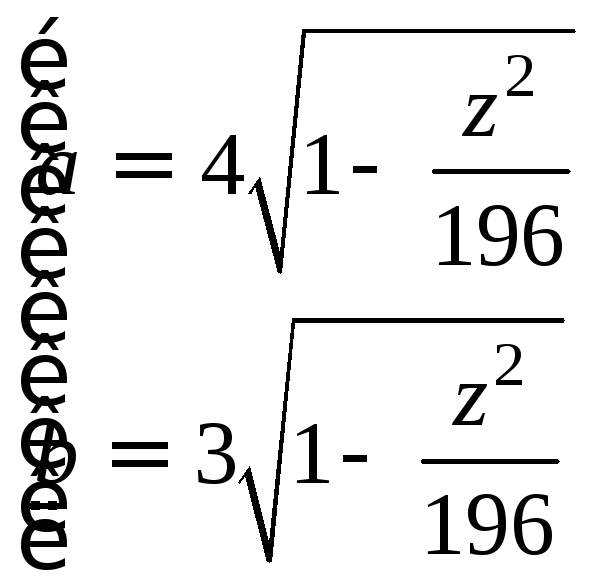 ,
S
(z)
=
а
b
= 12
,
S
(z)
=
а
b
= 12
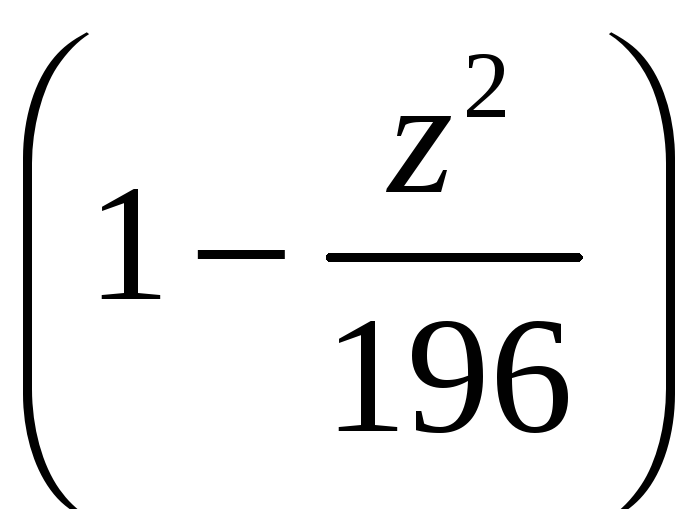 .
. =
=
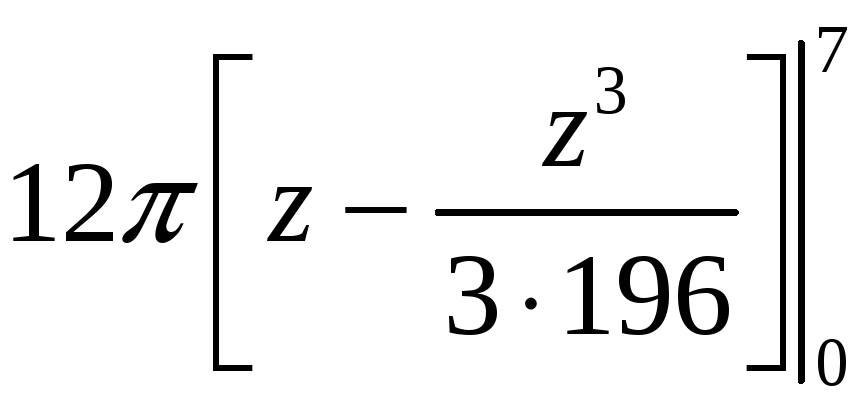 =
= 12
=
= 12

241,903.
241,903.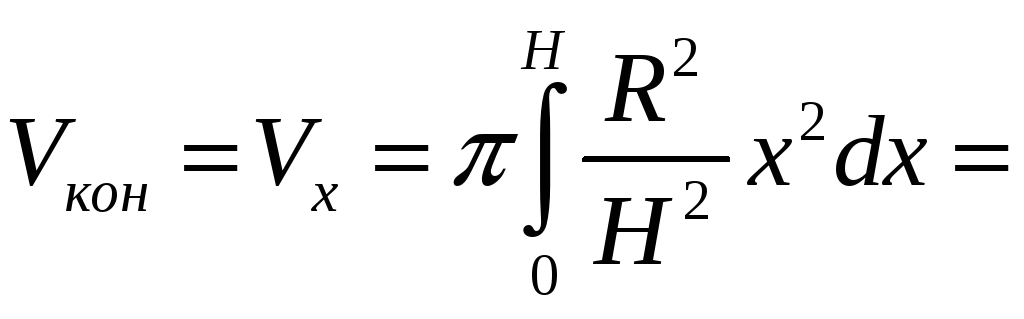
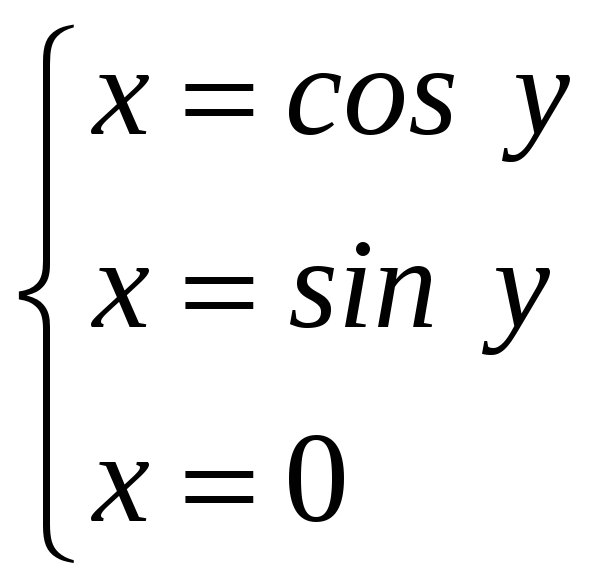

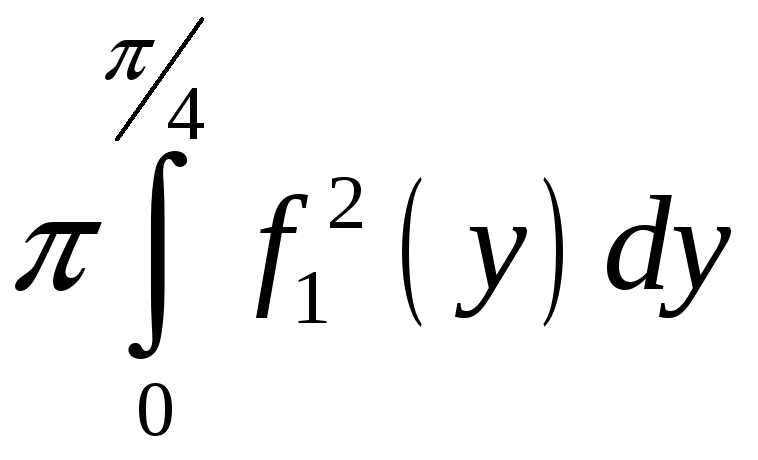 +
+
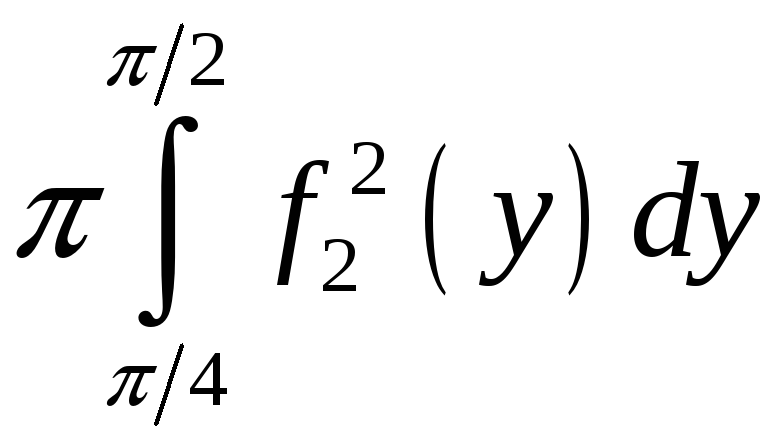
 +
+
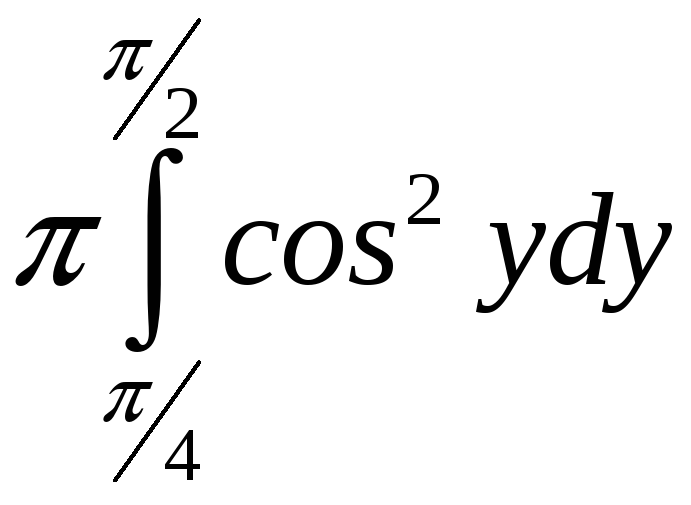 =
=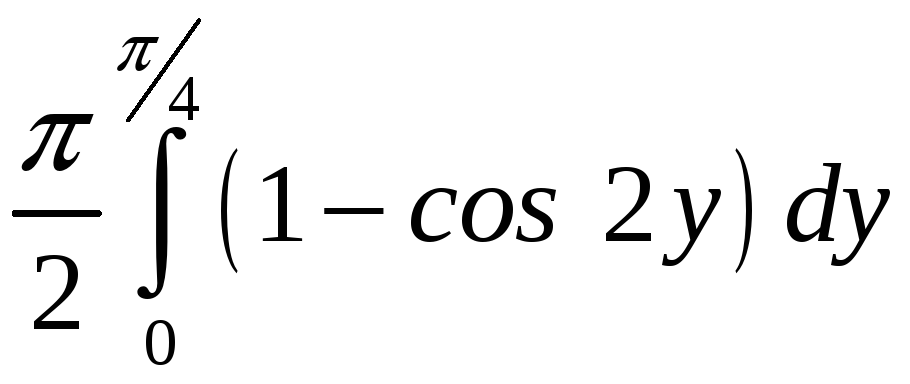 +
+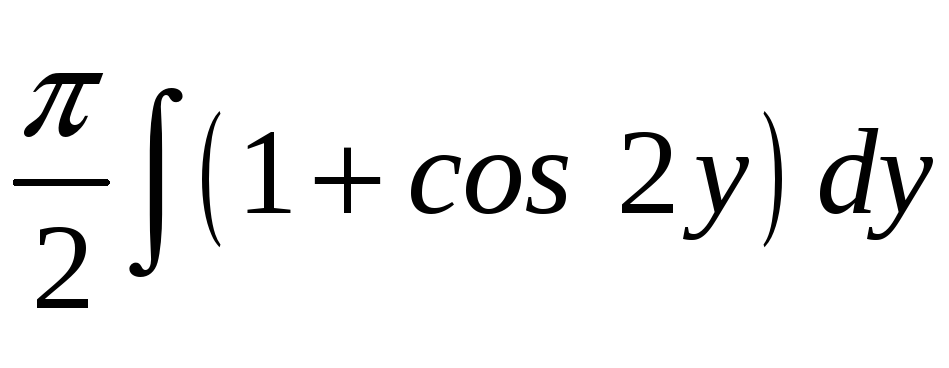 =
=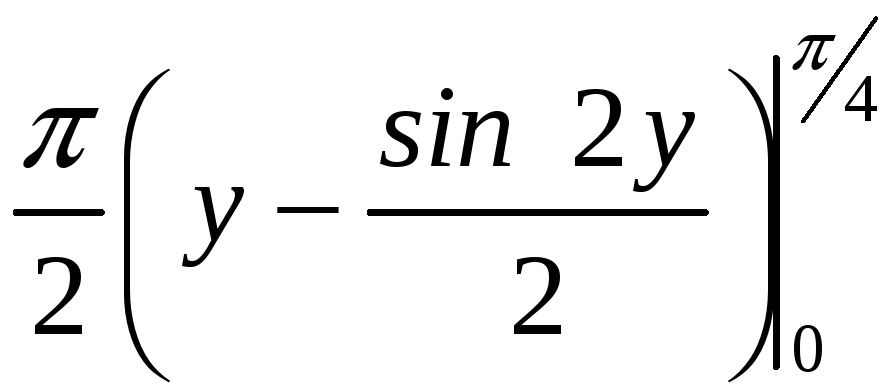 +
+
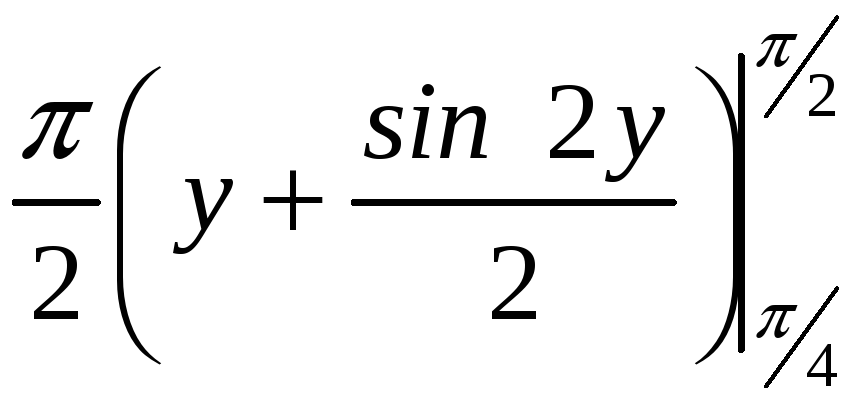 =
= =
=
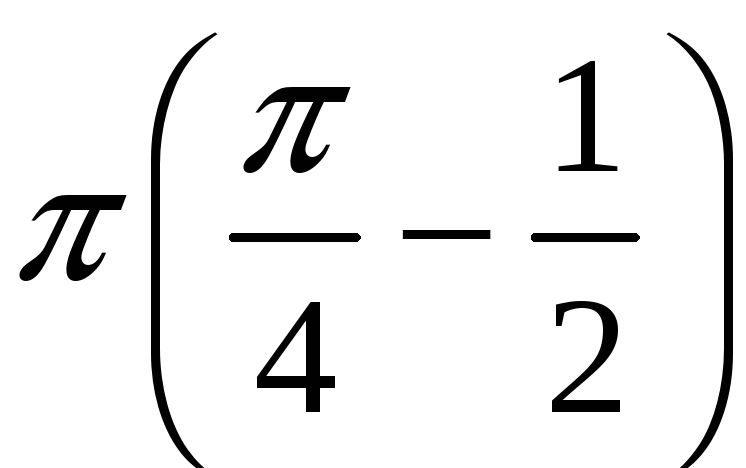
0,896602.
0,896602.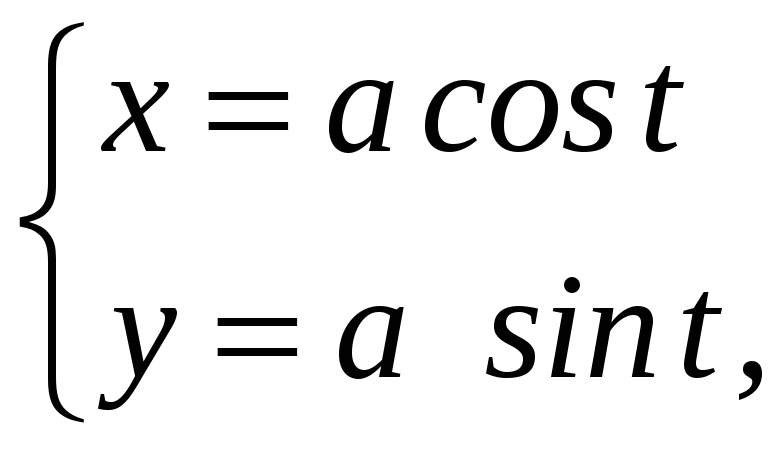
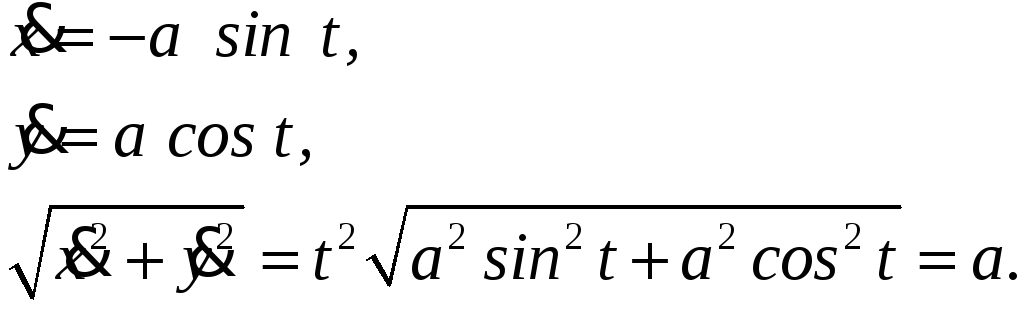
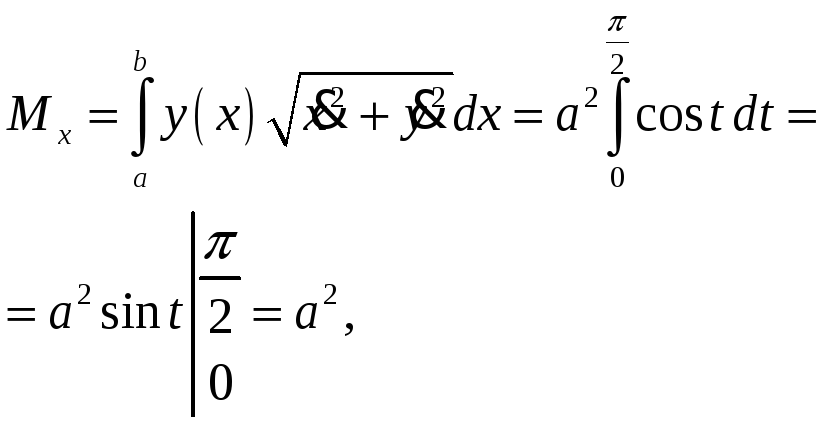



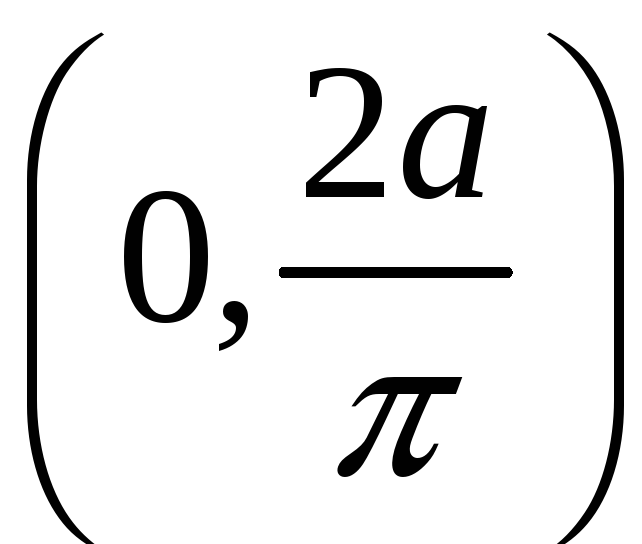 .
.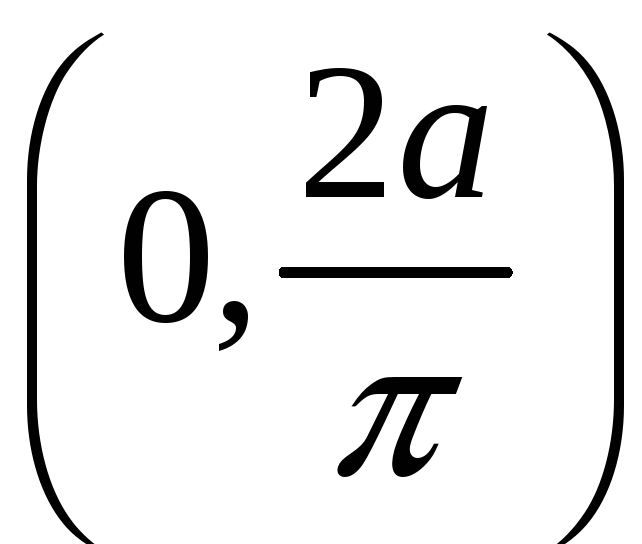
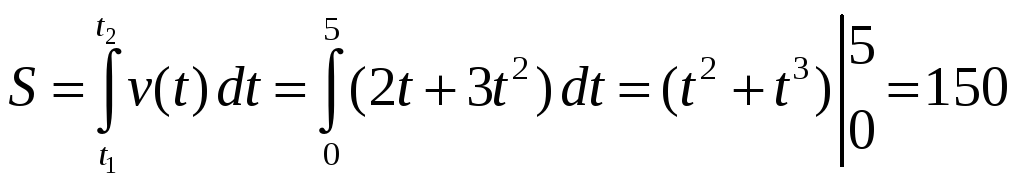 м.
м. .
. ,
М
– масса Земли, r
– расстояние
массы m
от центра Земли, k
– гравитационная постоянная.
,
М
– масса Земли, r
– расстояние
массы m
от центра Земли, k
– гравитационная постоянная.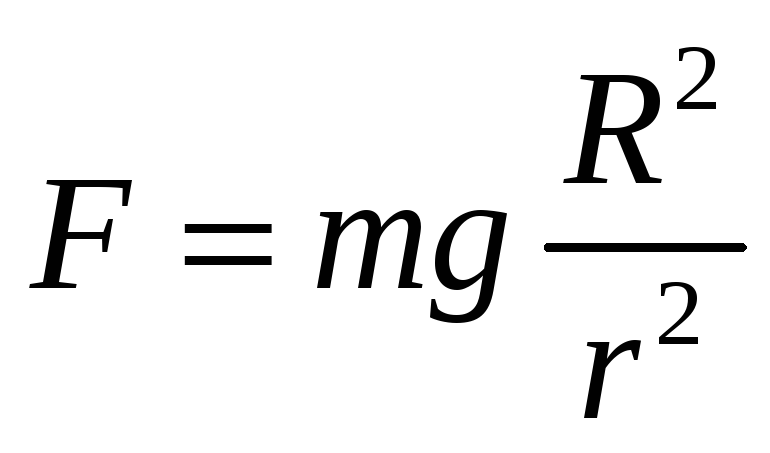 .
.
 ассмотрим
элементарную прямоугольную площадку,
находящуюся на глубине x,
имеющую основание b
и высоту dx.
ассмотрим
элементарную прямоугольную площадку,
находящуюся на глубине x,
имеющую основание b
и высоту dx.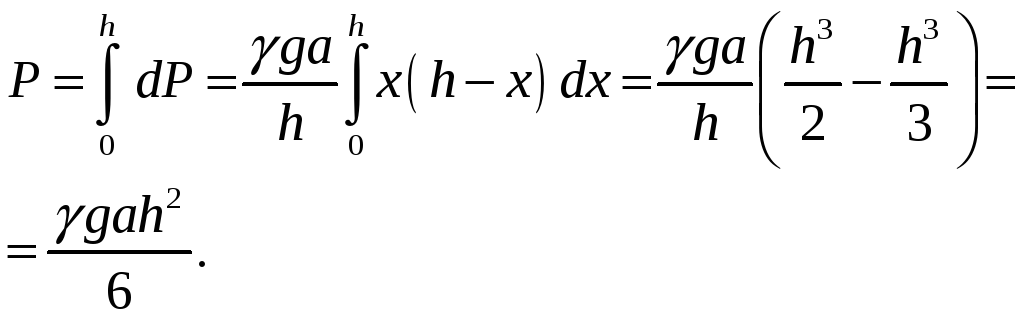
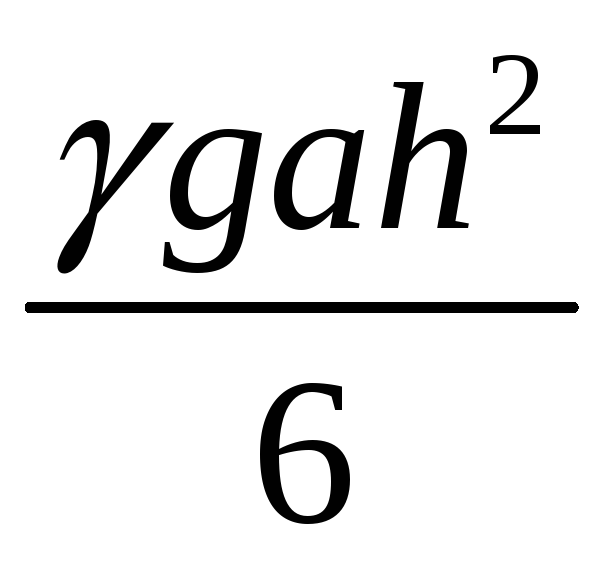
 ;
;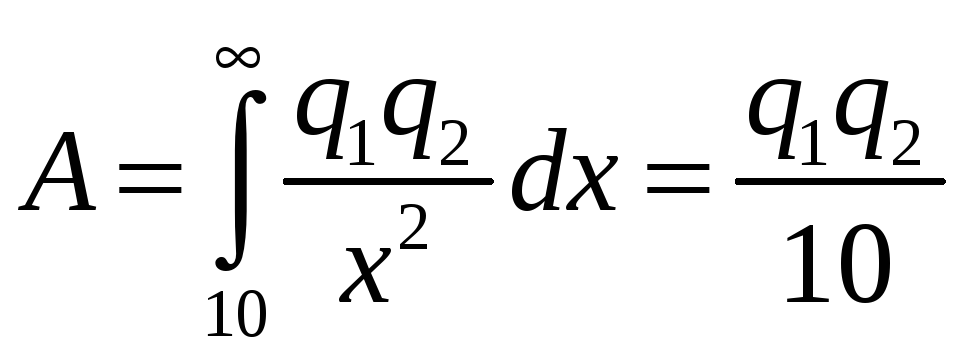 .
.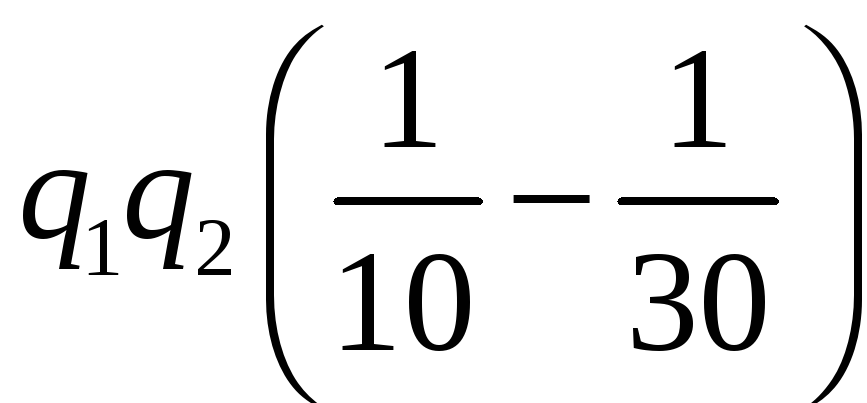 ,
,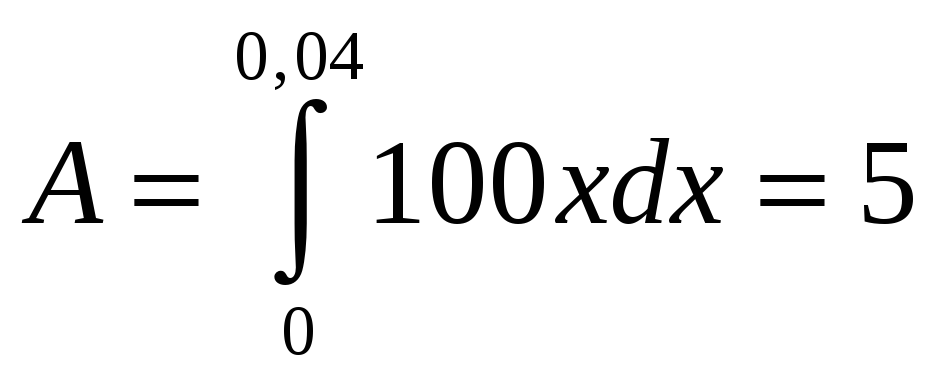
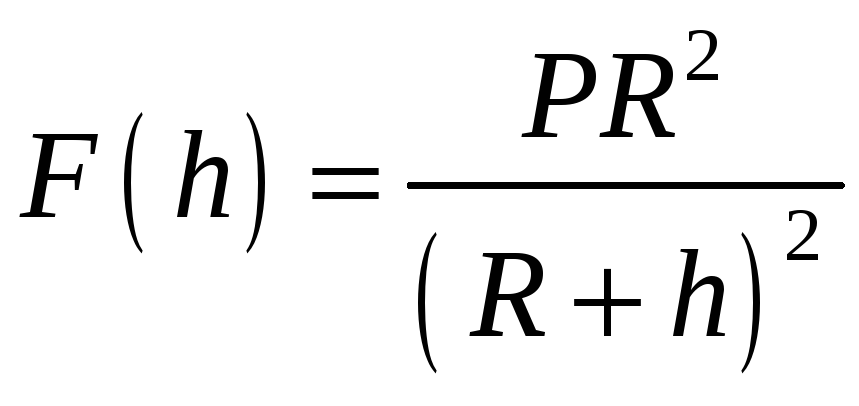 .
.
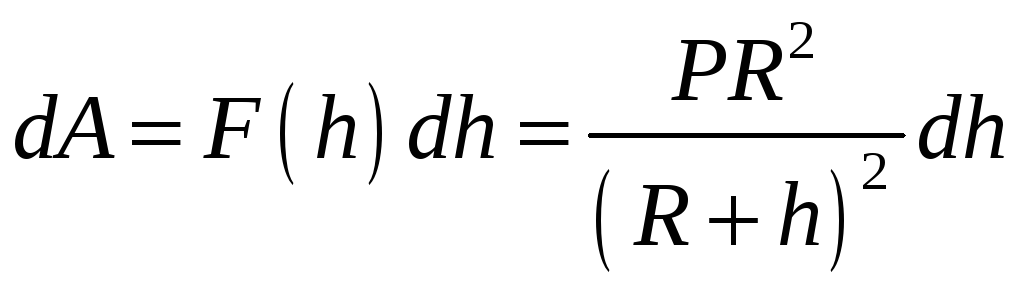 ,
,
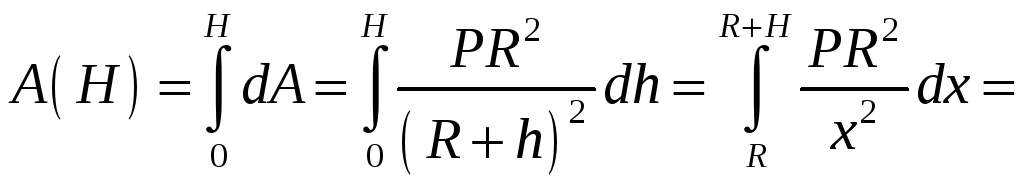
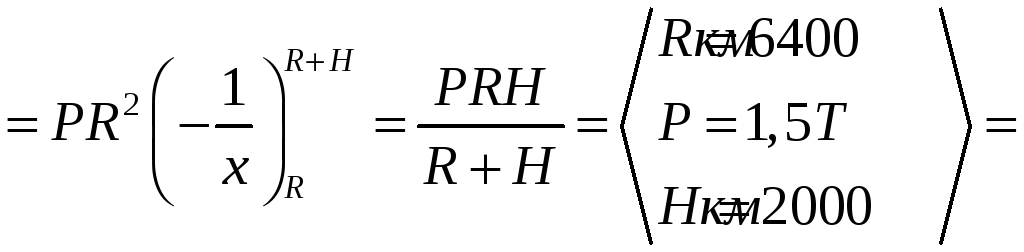
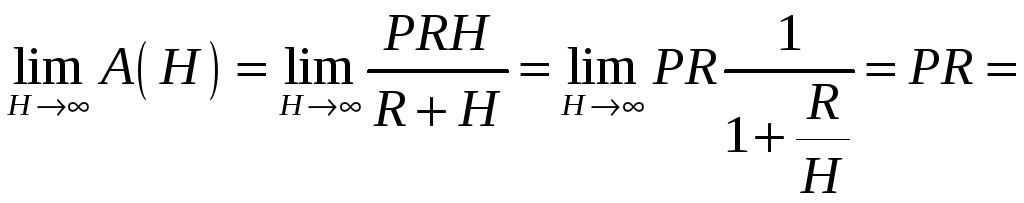
 дельный
вес воды
дельный
вес воды
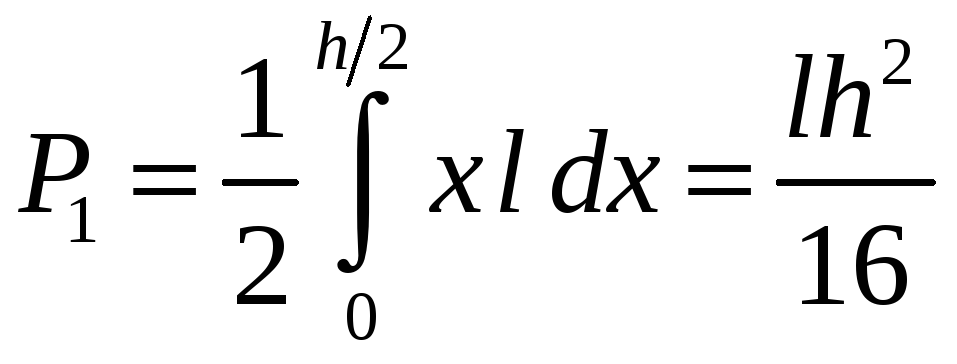 .
Давление
на глубине
.
Давление
на глубине
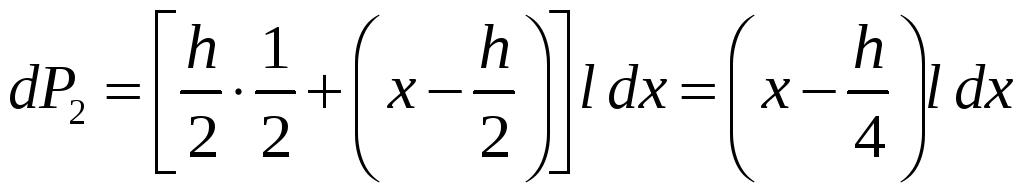 ,
,
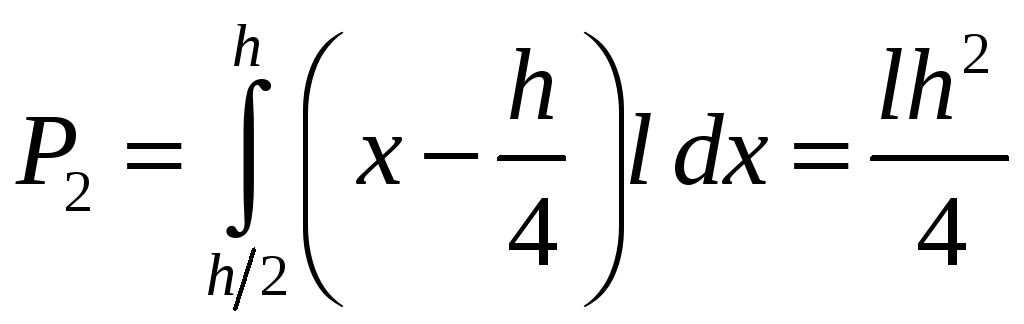 .
Полное
давление смеси на стенку:
.
Полное
давление смеси на стенку:
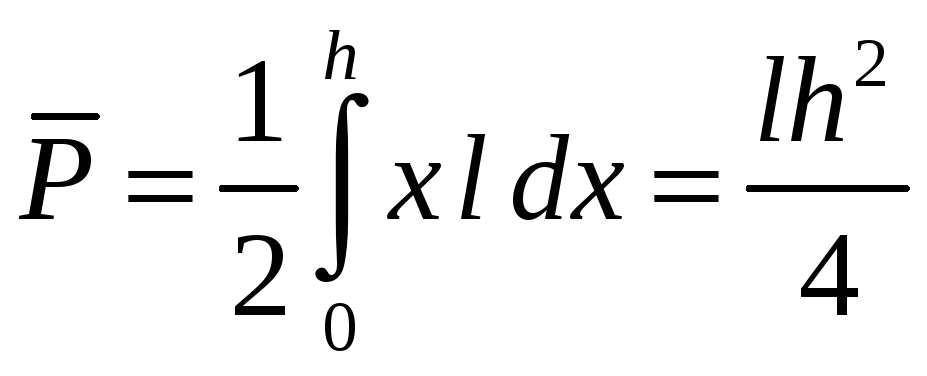 ,
,