
- •Пп № 3. Системы линейных уравненИй основные определения и формулы Системы n линейных уравнений с n неизвестными
- •Правило Крамера
- •Системы m линейных уравнений с n неизвестными
- •Теорема КронекераКапелли
- •Однородные системы
- •Метод последовательных исключений Жордана-Гаусса решения систем m линейных уравнений с n неизвестными Эквивалентные преобразования системы:
Пп № 3. Системы линейных уравненИй основные определения и формулы Системы n линейных уравнений с n неизвестными

В
матричной форме система имеет вид
![]() ,
где
,
где
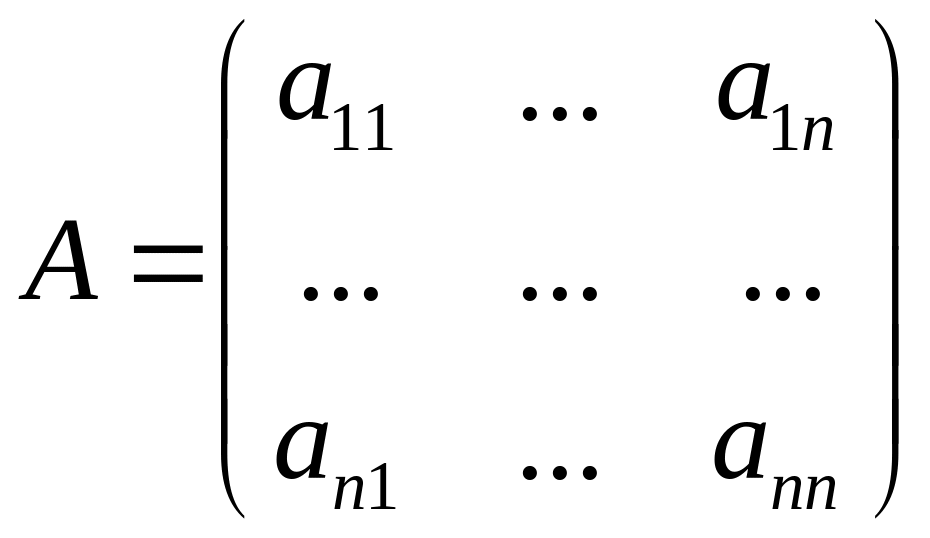 ,
,
 ,
,
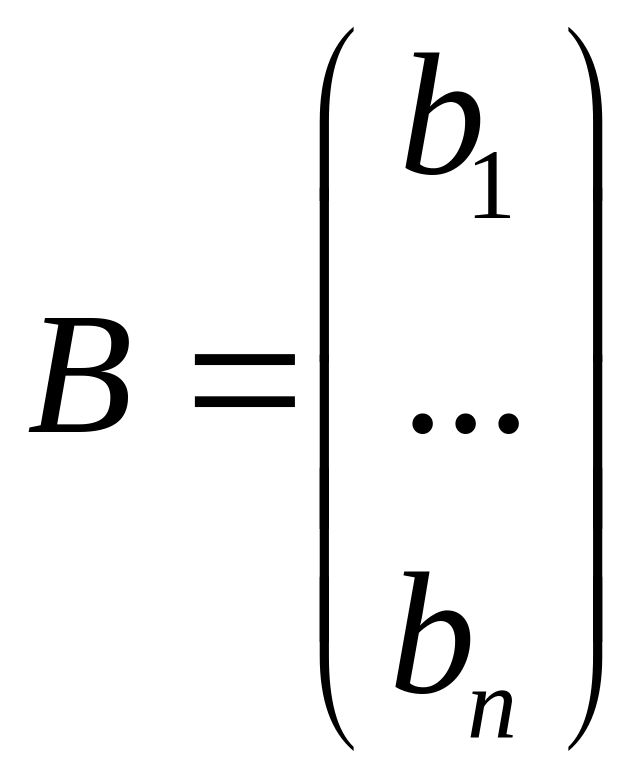 .
.
Правило Крамера
Если
главный определитель системы линейных
уравнений
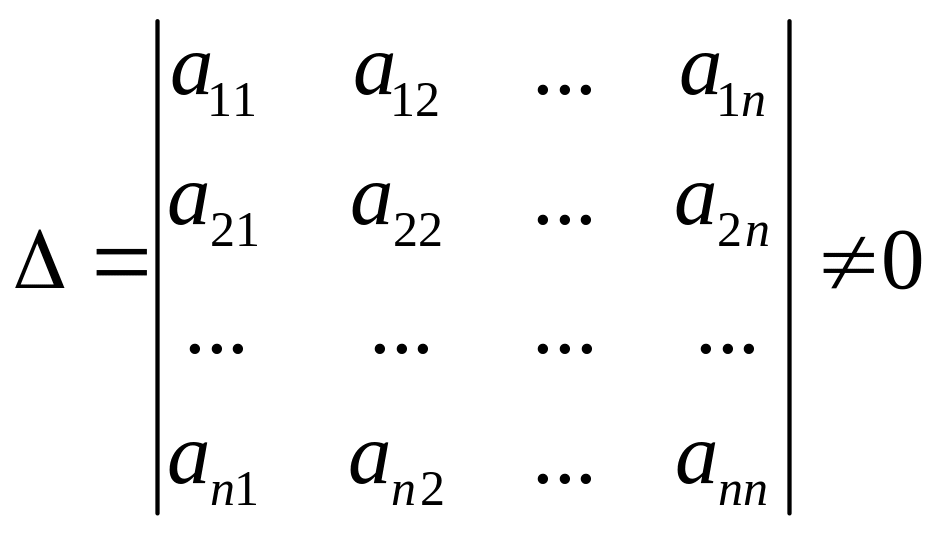 ,
то есть матрица А
имеет
обратную
,
то есть матрица А
имеет
обратную![]() ,
то
система имеет, и притом единственное
решение
,
то
система имеет, и притом единственное
решение
![]() ,
,
или, в покомпонентной записи,
![]() ,
,
![]() ,
,
где
![]() - определители, получаемые из главного
определителя системы
- определители, получаемые из главного
определителя системы
![]() заменой
заменой
![]() -го
столбца на столбец свободных членов:
-го
столбца на столбец свободных членов:
![]() ,
,![]() ,…
,…
![]() .
.
Системы m линейных уравнений с n неизвестными
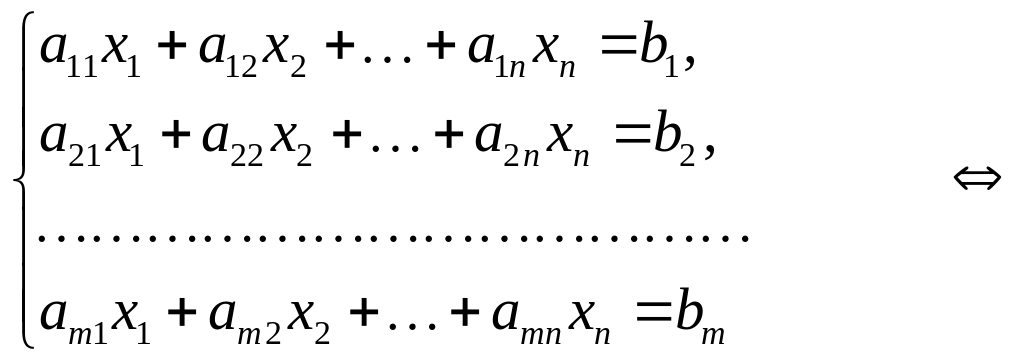 ,
,
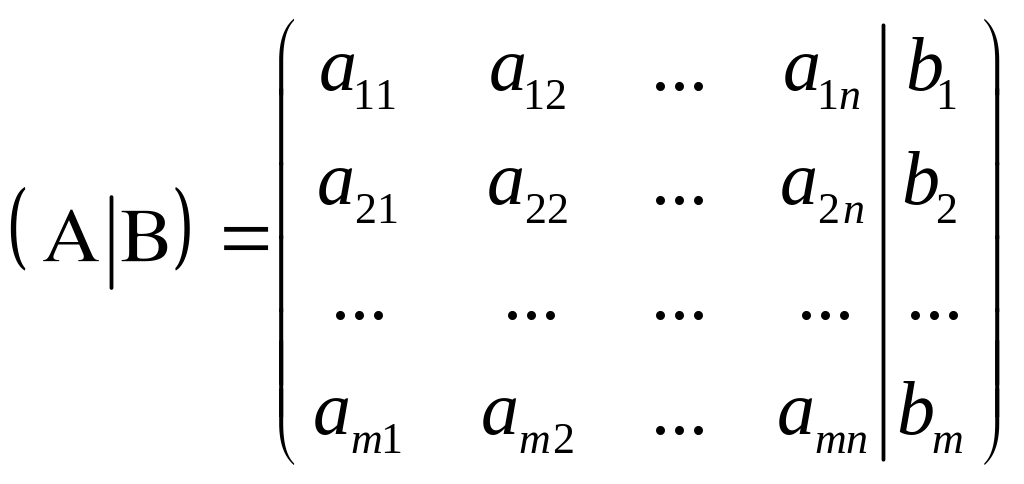 -
расширенная матрица системы,
-
расширенная матрица системы,
 - основная матрица системы,
- основная матрица системы,
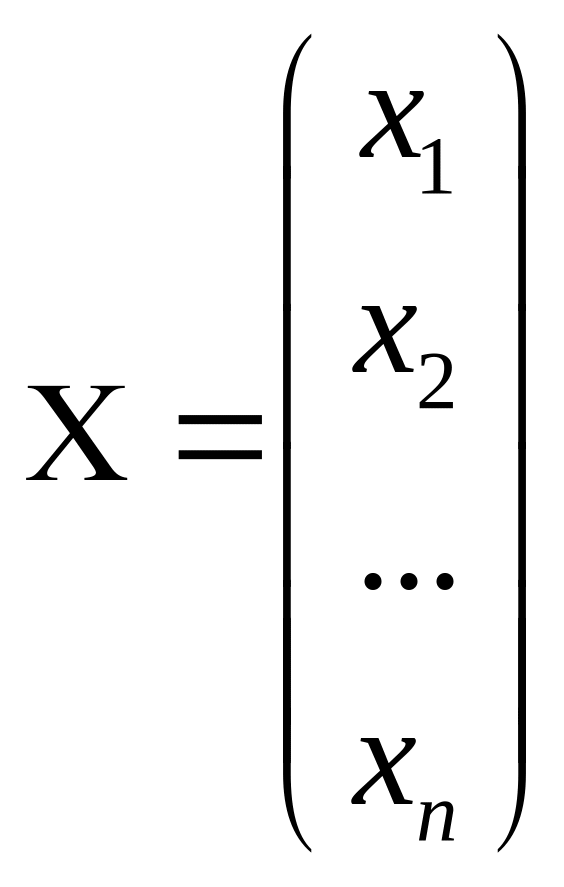 - столбец неизвестных,
- столбец неизвестных,
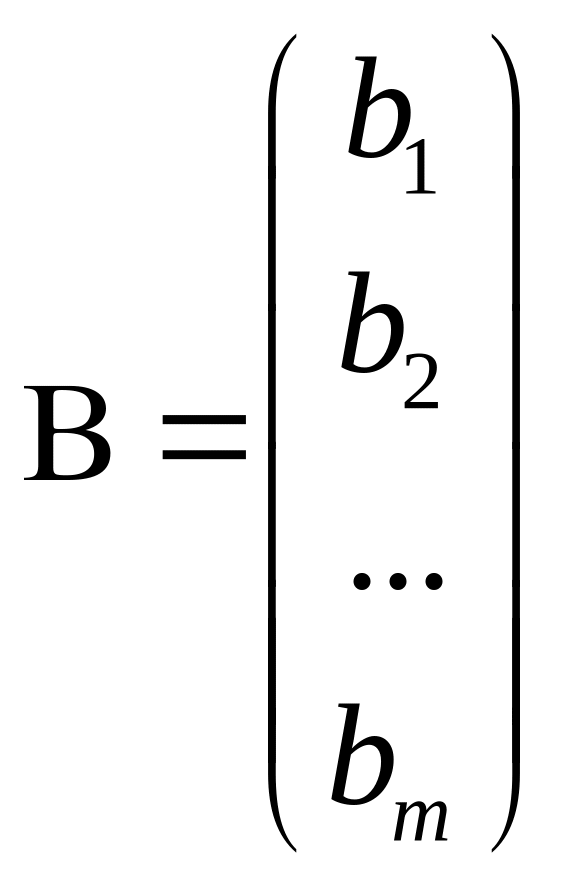 - столбец свободных членов.
- столбец свободных членов.
Система
линейных уравнений называется
неоднородной,
если матрица
![]() не является нульматрицей
не является нульматрицей
![]() ,
и называется однородной,
если
,
и называется однородной,
если
![]() .
.
Система линейных уравнений называется совместной, если она имеет решения, и называется несовместной - в противном случае. Система называется определенной, если она имеет единственное решение, и называется неопределенной, если она имеет бесконечное множество решений.
Теорема КронекераКапелли
Для того чтобы система m линейных уравнений с n неизвестными была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу расширенной матрицы системы:
![]() .
.
Если
![]() то система решений не имеет.
то система решений не имеет.
Eсли , то возможны два случая:
1)
![]() (числу неизвестных)
решение единственное и может быть
получено по формулам Крамера;
(числу неизвестных)
решение единственное и может быть
получено по формулам Крамера;
2)
![]()
решений бесконечно много.
решений бесконечно много.
Схема отыскания
решения системы m
линейных уравнений с n
неизвестными в случае бесконечного
числа решений, если
![]() и
и
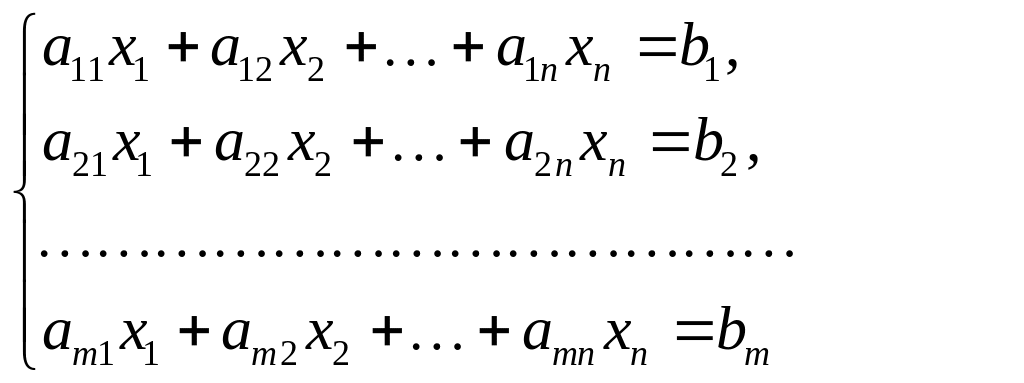
1)
Из коэффициентов матрицы системы выберем
любой отличный от нуля минор порядка
![]()
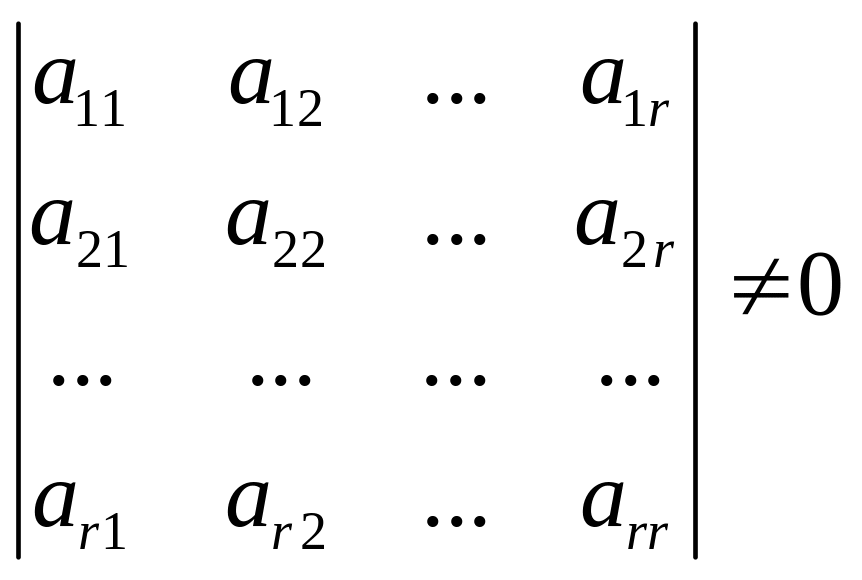 в
качестве базисного,
в
качестве базисного,
![]() – базисные
неизвестные, а
– базисные
неизвестные, а
![]() – свободные неизвестные.
– свободные неизвестные.
2) Перенесем свободные неизвестные в правую часть уравнений системы:
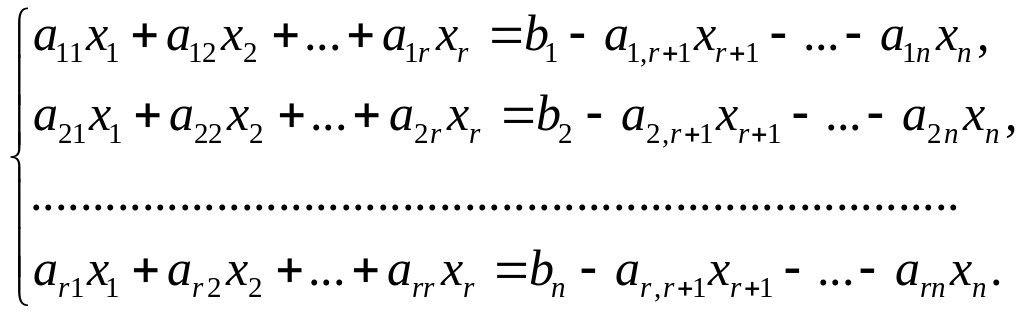
3) Найдем решение этой системы по формулам Крамера или матричным способом.
При этом базисные неизвестные выражаются через свободные.
Если
свободные неизвестные принимают значения
![]() ,
то общее решение неоднородной системы
имеет вид:
,
то общее решение неоднородной системы
имеет вид:
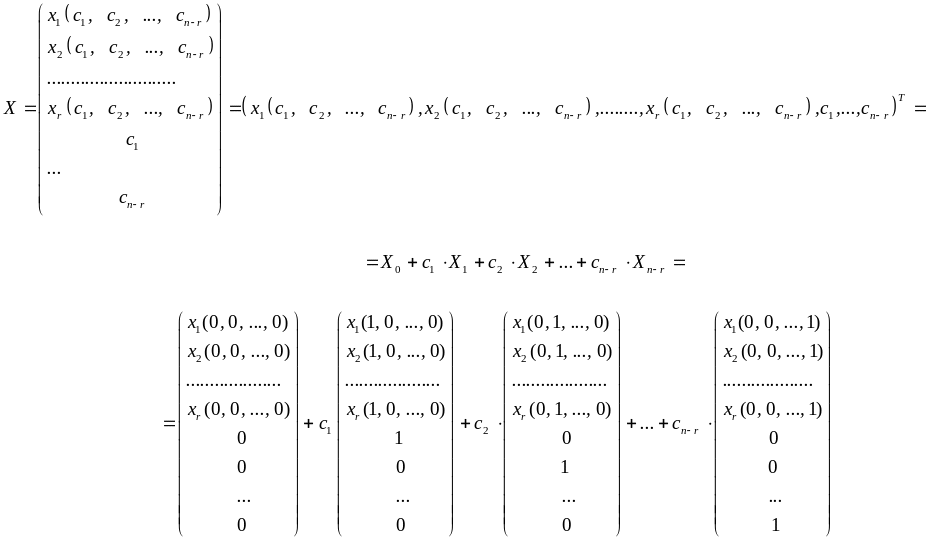 ,
,
здесь система вектор-столбцов
![]()
называется фундаментальной системой решений. Фундаментальная система решений получается из общего решения, если свободным неизвестным придавать поочередно значение 1, полагая остальные равными 0.
Однородные системы
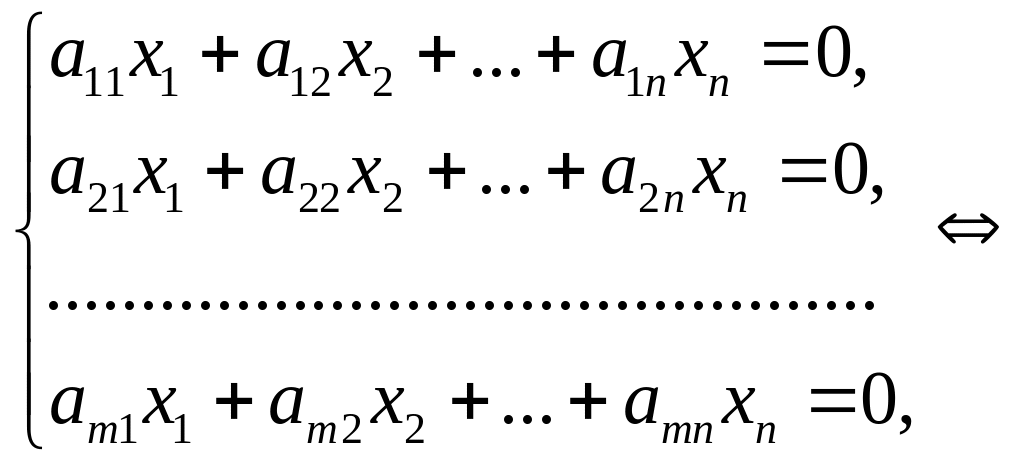
![]() .
.
Однородная система
всегда совместна (![]() ),
так как имеет тривиальное решение
),
так как имеет тривиальное решение
![]() .
.
Для того чтобы
однородная система имела ненулевое
(нетривиальное) решение, необходимо и
достаточно, чтобы
![]() =
=![]() .
.
Для того чтобы однородная система n линейных уравнений с n неизвестными

имела ненулевое
решение, необходимо и достаточно, чтобы
![]() .
.
Если
![]() ,
то заведомо
,
то заведомо
![]() ,
возникают свободные неизвестные
,
возникают свободные неизвестные
![]() ,
система имеет нетривиальные решения,
причем их бесконечно много.
,
система имеет нетривиальные решения,
причем их бесконечно много.
Общее решение при имеет вид:

и
совпадает с соответствующим общим
решением неоднородной системы при
![]() .
.
Метод последовательных исключений Жордана-Гаусса решения систем m линейных уравнений с n неизвестными Эквивалентные преобразования системы:
1) перемена местами двух любых уравнений системы;
2)
умножение любого уравнения системы на
произвольное число
![]() ;
;
3) прибавление к одному уравнению системы другого уравнения, умноженного на произвольное число .
Элементарные преобразования матрицы не изменяют ее ранга.
Элементарным
преобразованиям уравнений соответствуют
элементарные преобразования элементов
расширенной матрицы системы
![]() .
.
С помощью элементарных преобразований над строками и перестановкой столбцов расширенная матрица системы может быть приведена к виду
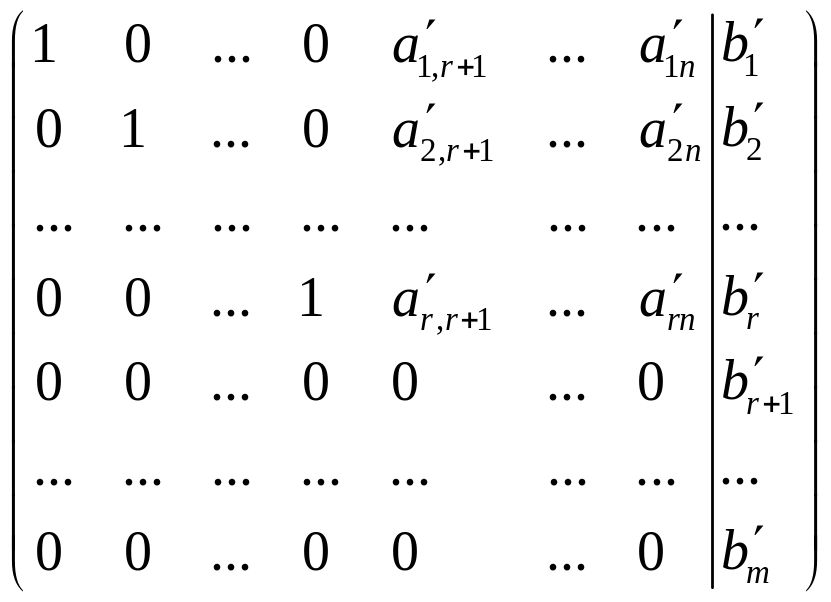 ,
,
и система принимает вид:
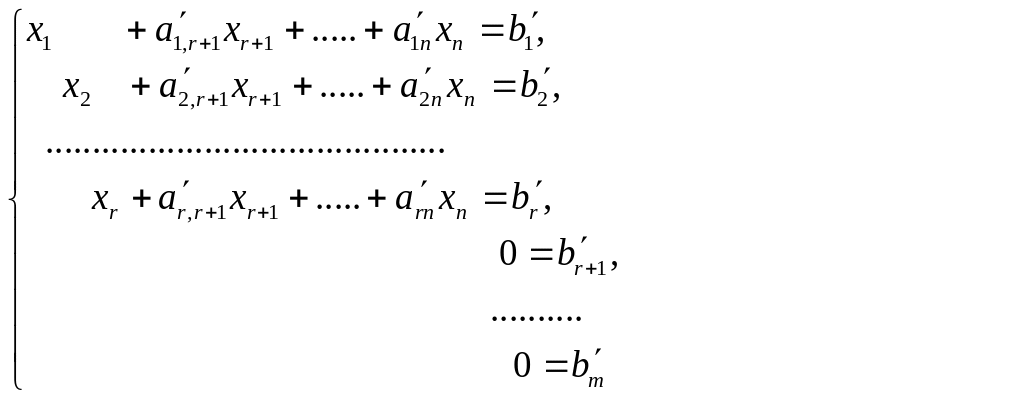 .
.
Если
хотя бы одно из чисел
![]() ,
….,
,
….,
![]() отлично от нуля, то система несовместна.
отлично от нуля, то система несовместна.
Если
=….=
=
0, то система совместна и выражения для
базисных неизвестных
![]() через свободные
через свободные
![]() очевидны.
очевидны.
Сформулируем
алгоритм Жордана-Гаусса
как
преобразование строк матрицы
к верхнему треугольному виду, которое
позволяет не только вычислить ранги
матриц
![]() и
и
![]() ,
но и записать решение системы.
,
но и записать решение системы.
ПП №3. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИй
|
||
№ п/п |
Задание |
Ответ |
ПП 3.№1. |
Решите систему
линейных уравнений матричным методом
РЕШЕНИЕ:
|
|
ПП 3.№2. |
Решите
систему
РЕШЕНИЕ:
по теореме Кронекера – Капелли система несовместна.
|
несовместна |
ПП 3.№3. |
Решите систему
линейных уравнений
и ответьте на вопросы об этой системе. РЕШЕНИЕ:
По
формулам Крамера
Данная система линейных уравнений: 1) однородна - нет; 2) неоднородна - да; 3) основная матрица системы имеет ранг, равный единице - нет; 4) основная матрица системы имеет ранг, равный двум - нет; 5) основная матрица системы имеет ранг, равный трем - да; 6) основная матрица системы имеет ранг больше трех - нет; 7) ранг прямой матрицы системы не равен рангу ее расширенной матрицы - нет; 8) ранг прямой матрицы системы равен рангу ее расширенной матрицы - да; 9) система несовместна - нет; 10) система совместна - да; 11) может быть решена методом Крамера - да; 12) может быть решена методом Гаусса - да; 13) имеет базисный минор первого порядка - нет; 14) имеет базисный минор второго порядка - нет; 15) имеет базисный минор третьего порядка - да; 16) имеет базисный минор более третьего порядка - нет; 17) имеет одно базисное неизвестное - нет; 18) имеет два базисных неизвестных - нет; 19) имеет более двух базисных неизвестных - да; 20) не имеет свободных неизвестных - да; 21) имеет одно свободное неизвестное - нет; 22) имеет более двух свободных неизвестных - нет; 23) решений не имеет - нет; 24) имеет единственное решение - да; |
|
ПП 3.№4. |
Решите систему линейных уравнений
РЕШЕНИЕ: Запишем расширенную матрицу системы
Если
Вычислим основной
определитель матрицы системы
Чтобы получить
определитель
Аналогично
вычисляем
Отсюда
|
|
ПП 3.№5. |
Решите систему линейных уравнений
РЕШЕНИЕ: Запишем расширенную матрицу системы
Ранг основной матрицы системы равен единице и совпадает с рангом расширенной матрицы системы, следовательно, по теореме Кронекера – Капелли система линейных уравнений совместна. Она равносильна уравнению:
В качестве базисного
неизвестного выберем
Итак,
|
|
ПП 3.№6. |
Решите систему линейных уравнений
РЕШЕНИЕ: Запишем расширенную матрицу системы
В левом верхнем
углу матрицы стоит треугольный
определитель
Восстановим по полученной матрице решение системы уравнений:
Базисный минор
содержит базисные неизвестные
,
|
|
ПП 3.№7. |
Решите систему линейных уравнений
РЕШЕНИЕ: Воспользуемся методом Гаусса. Запишем расширенную матрицу системы:
В левом верхнем углу стоит треугольный определитель третьего порядка
Чтобы получить
ее решение, получим нули под главной
диагональю базисного минора с помощью
преобразования
Восстановим по
матрице решение системы уравнений
при
|
|
ПП 3.№8. |
Решите систему линейных уравнений
РЕШЕНИЕ: Запишем расширенную матрицу системы уравнений
Система несовместна,
так как ранг основной матрицы системы
не равен рангу расширенной матрицы.
Убедимся, что ранг основной матрицы
меньше ранга расширенной матрицы.
Чтобы не работать с дробями, проделаем
вспомогательное преобразование
Таким образом,
элемент
С помощью
преобразования
Ранг прямой матрицы равен 3, так как она содержит минор
третьего порядка и не содержит отличных от нуля определителей большего порядка. Ранг расширенной матрицы равен 4, так как она содержит минор
четвертого порядка. Следовательно, по теореме Кронекера – Капелли система несовместна. |
несовместна |
ПП 3.№9. |
Решите систему уравнений
РЕШЕНИЕ: Ранг основной матрицы системы равен двум и совпадает с рангом расширенной матрицы системы, следовательно, по теореме Кронекера – Капелли система линейных уравнений совместна. В качестве базисных
неизвестных выберем
Данная система линейных уравнений: 1) однородна - да; 2) неоднородна - нет; 3) основная матрица системы имеет ранг, равный единице - нет; 4) основная матрица системы имеет ранг, равный двум - да; 5) основная матрица системы имеет ранг, равный трем - нет; 6) основная матрица системы имеет ранг больше трех - нет; 7) ранг прямой матрицы системы не равен рангу ее расширенной матрицы - нет; 8) ранг прямой матрицы системы равен рангу ее расширенной матрицы - да; 9) система несовместна - нет; 10) система совместна - да; 11) может быть решена методом Крамера - нет; 12) может быть решена методом Гаусса - да; 13) имеет базисный минор первого порядка - нет; 14) имеет базисный минор второго порядка - да; 15) имеет базисный минор третьего порядка - нет; 16) имеет базисный минор более третьего порядка - нет; 17) имеет одно базисное неизвестное - нет; 18) имеет два базисных неизвестных - да; 19) имеет более двух базисных неизвестных - нет; 20) не имеет свободных неизвестных - нет; 21) имеет одно свободное неизвестное - да; 22) имеет более двух свободных неизвестных - нет; 23) решений не имеет - нет; 24) имеет единственное решение - нет; 25) имеет бесконечно много решений - да. |
|
ПП 3.№10. |
Решите
систему
РЕШЕНИЕ: Рассмотрим матрицу системы:
Следовательно,
Полагая
|
|
ПП 3.№ 11. |
Найти фундаментальную систему решений и общее решение однородной системы уравнений:
Матрица коэффициентов
имеет ранг r=2 (проверьте!). Выберем в качестве базисного минор
Тогда укороченная система имеет вид
откуда, полагая
Общее решение системы
Из общего решения находим фундаментальную систему решений
С использованием фундаментальной системы общее решение может быть записано в виде:
|
|

 ,
,
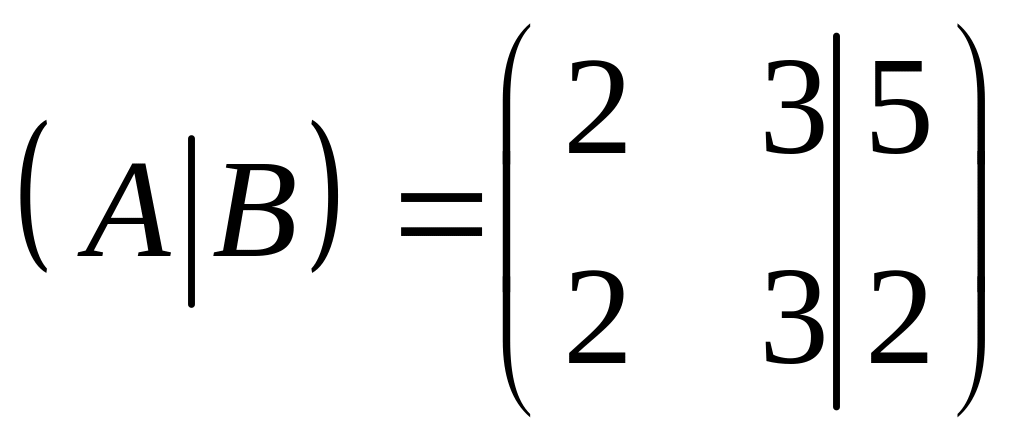 ,
,
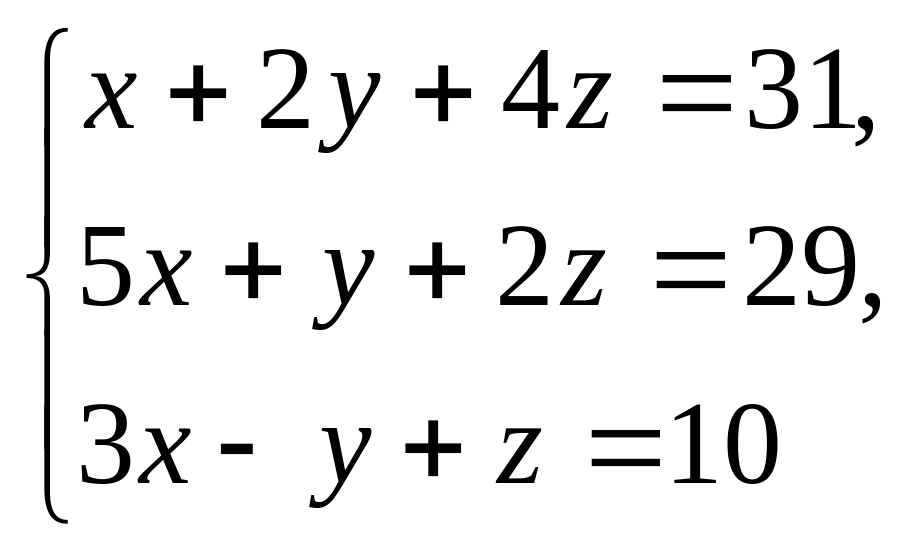
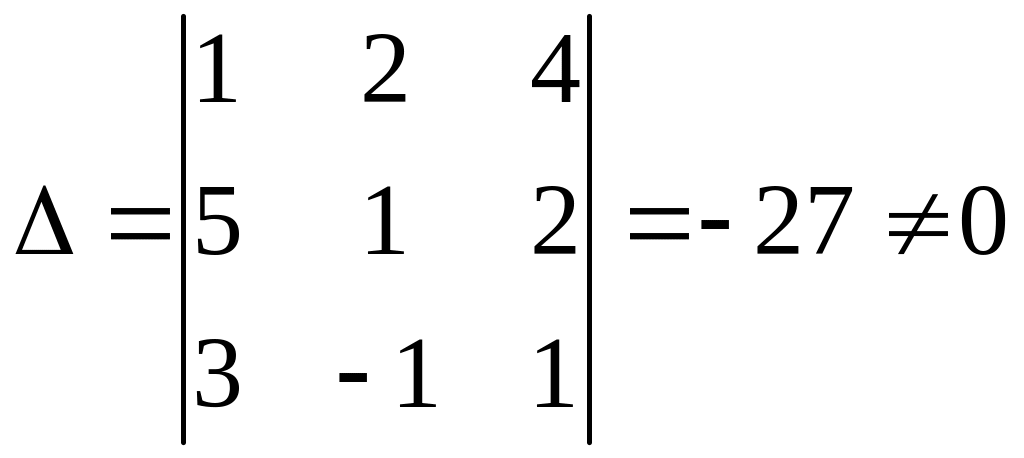 ,
,
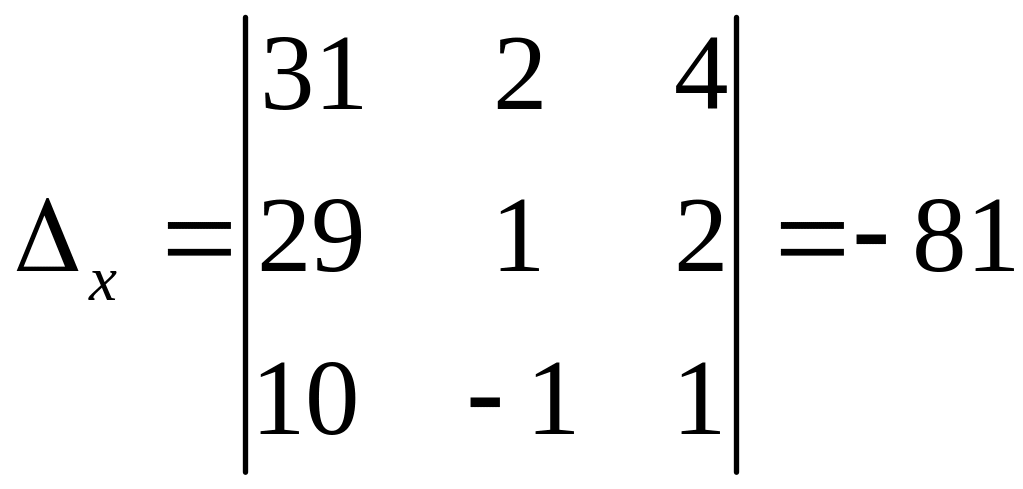 ,
,
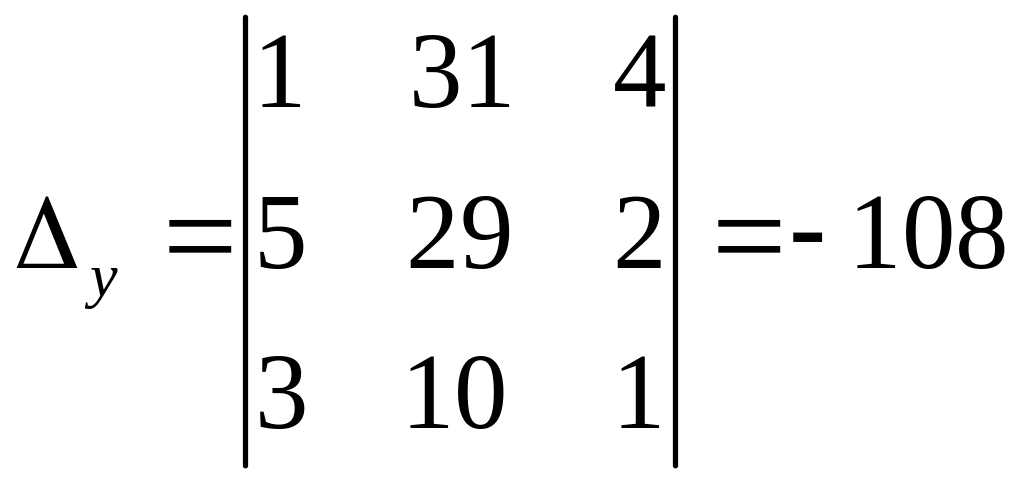 ,
,
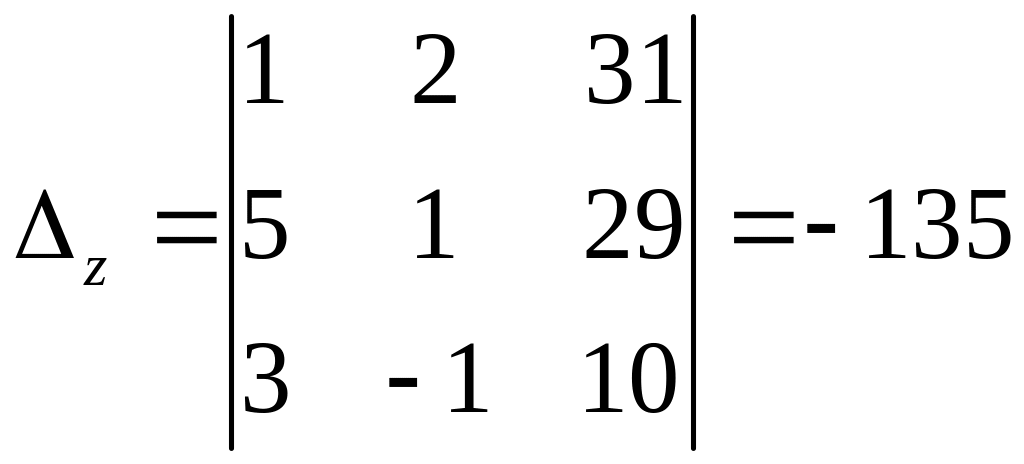 .
.
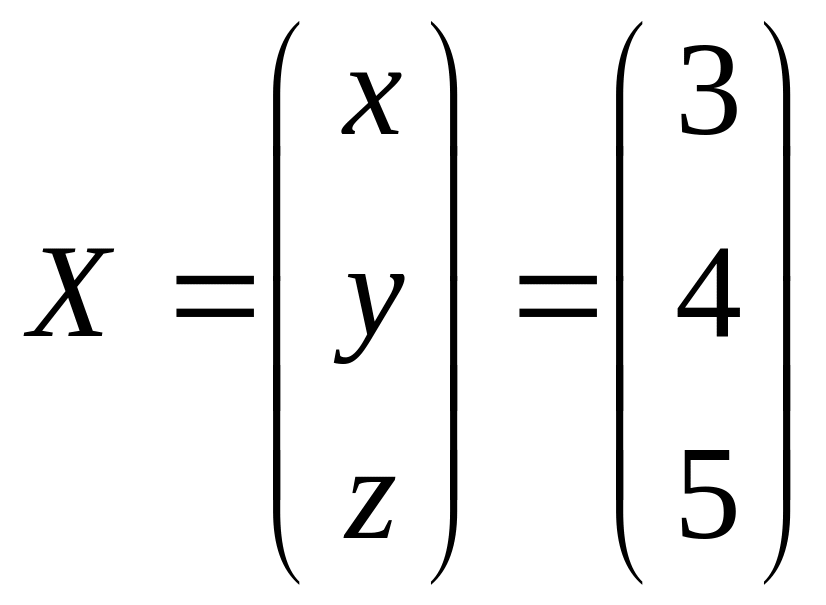 .
.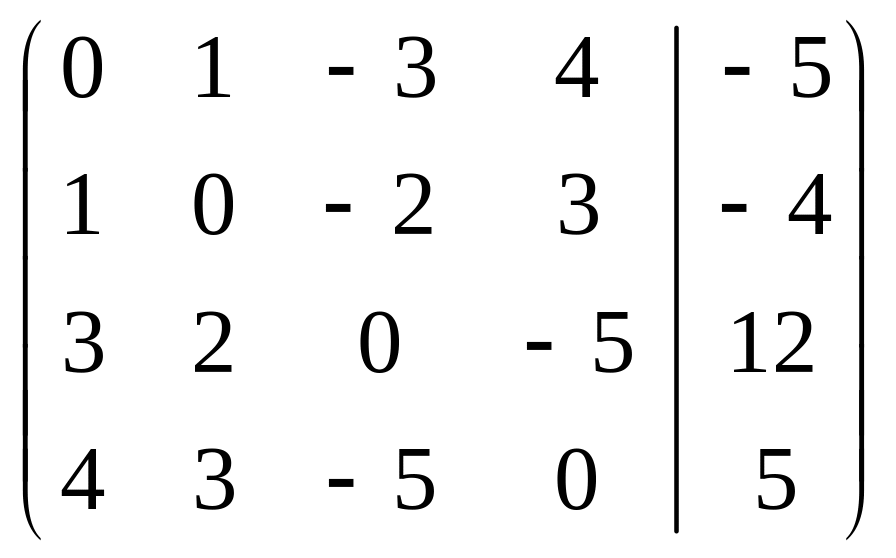 .
.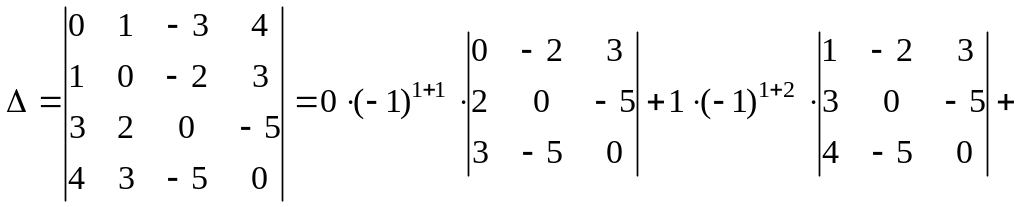
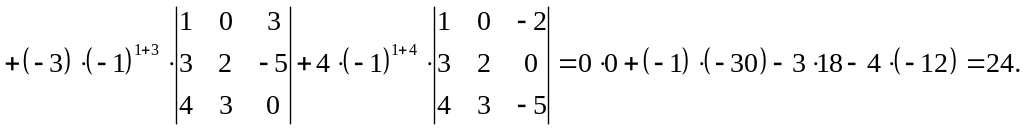

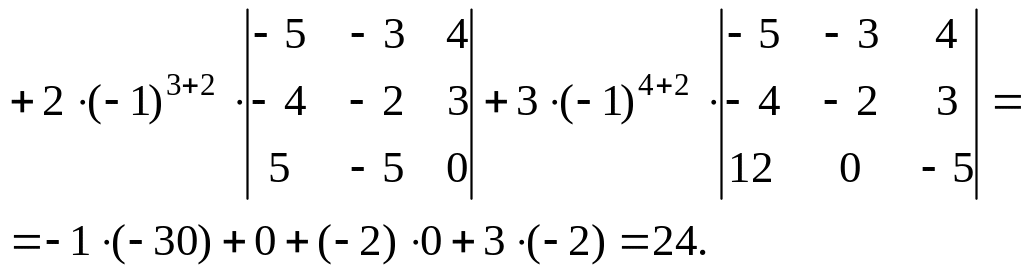
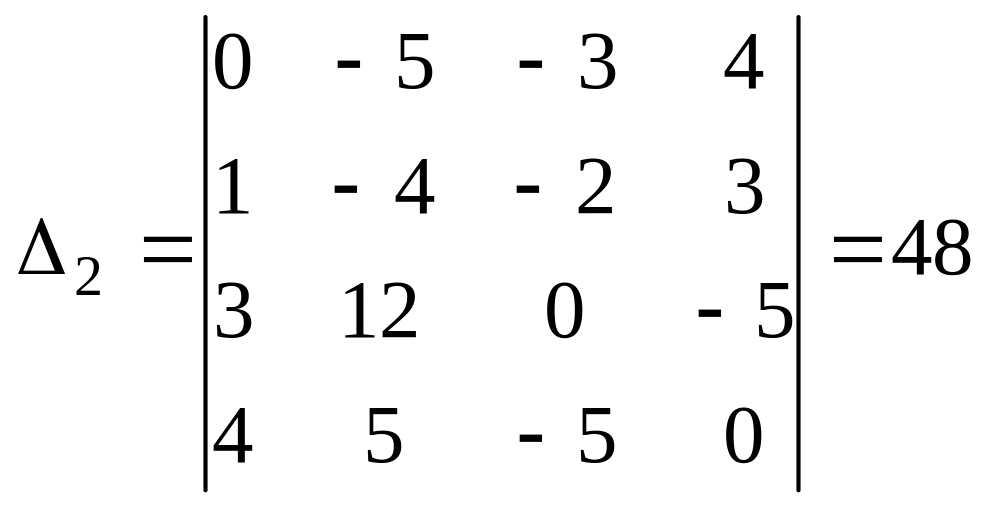 ,
,
 ,
,
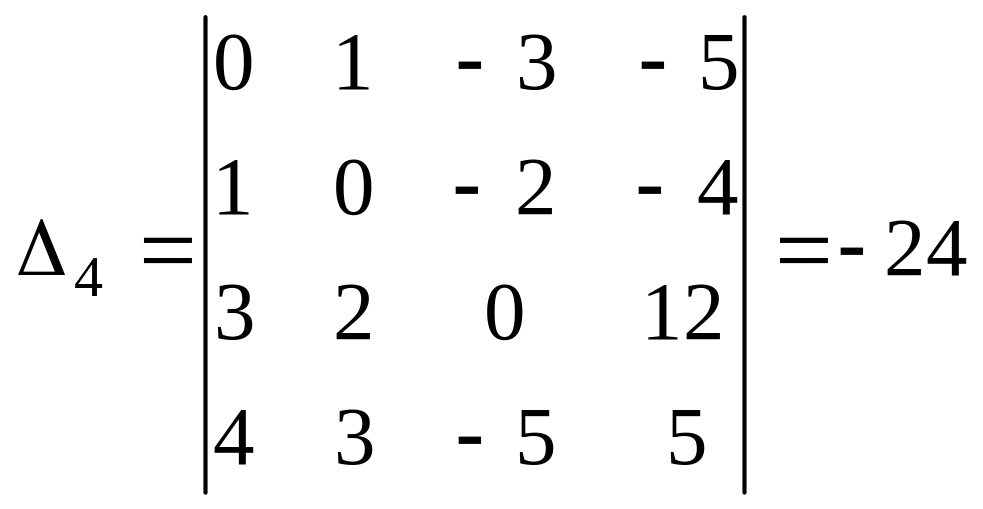 .
. .
.
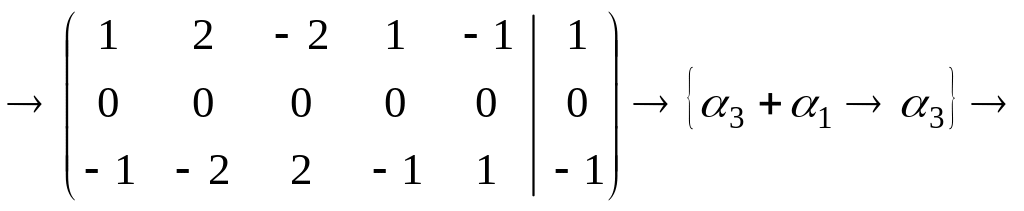
 .
. .
.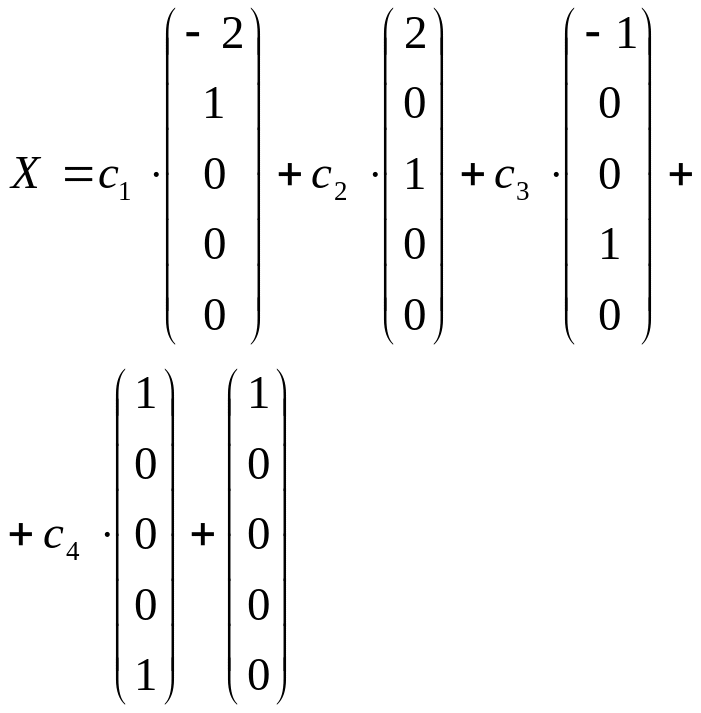


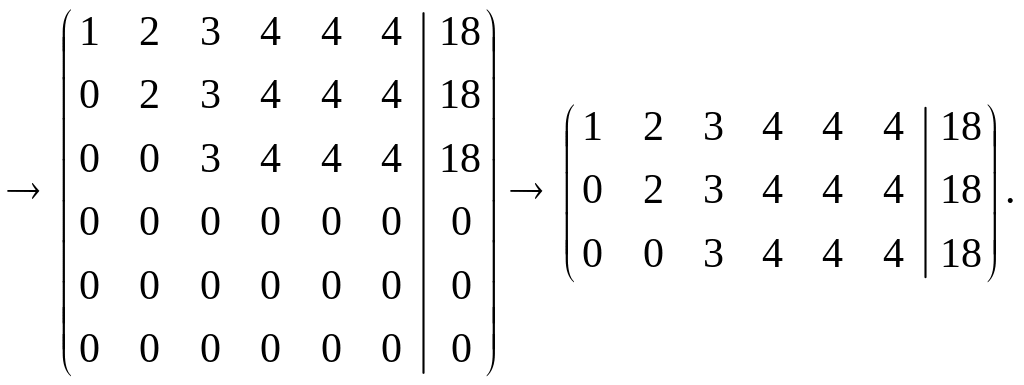
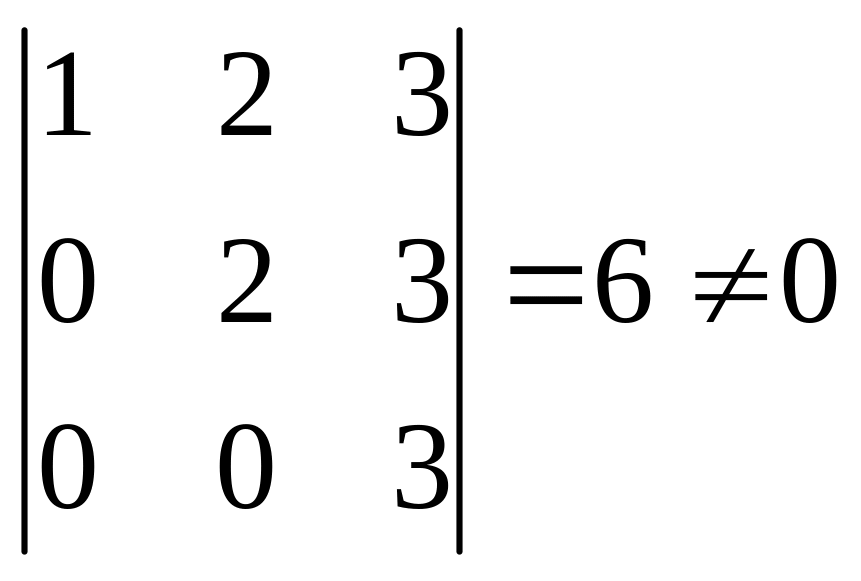 ,
его можно считать базисным минором.
Ранг основной матрицы системы линейных
уравнений равен трем и равен рангу ее
расширенной матрицы, следовательно,
система совместна по теореме Кронекера
– Капелли. Для удобства продолжим
преобразования матрицы и приведем
базисный минор не только к треугольному,
но и к диагональному виду. С помощью
преобразований
,
его можно считать базисным минором.
Ранг основной матрицы системы линейных
уравнений равен трем и равен рангу ее
расширенной матрицы, следовательно,
система совместна по теореме Кронекера
– Капелли. Для удобства продолжим
преобразования матрицы и приведем
базисный минор не только к треугольному,
но и к диагональному виду. С помощью
преобразований
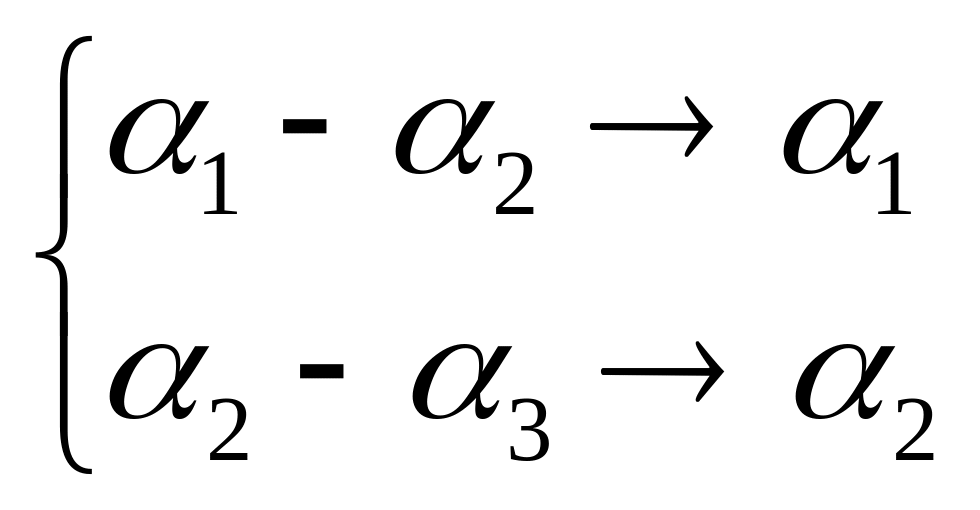 получим:
получим: .
.
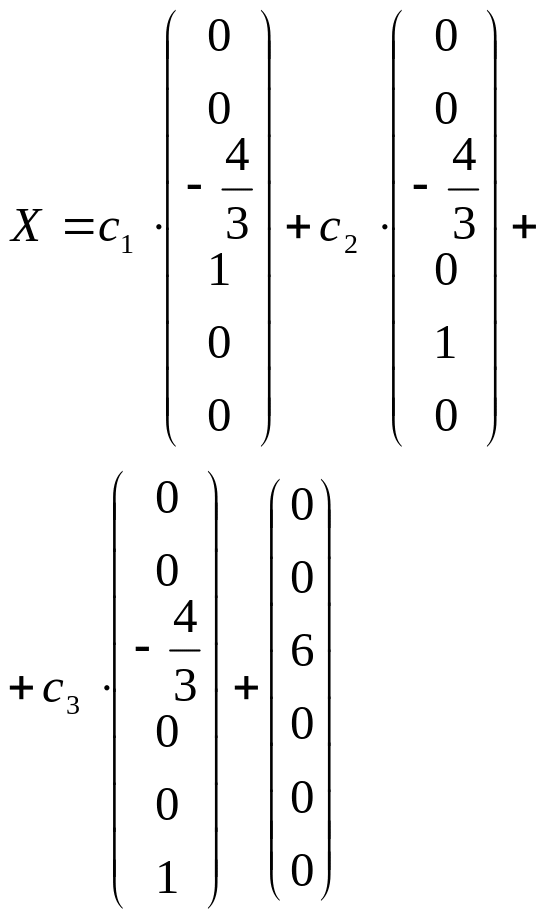
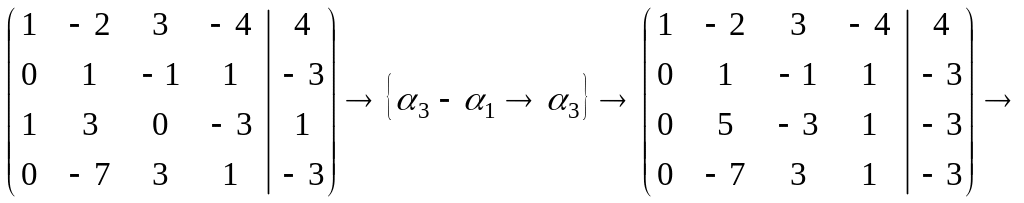

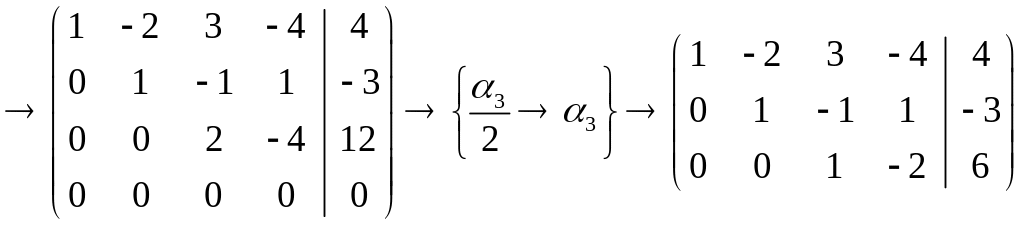 .
. ,
значит
ранг прямой матрицы системы равен 3,
равен рангу ее расширенной матрицы,
и система совместна.
,
значит
ранг прямой матрицы системы равен 3,
равен рангу ее расширенной матрицы,
и система совместна.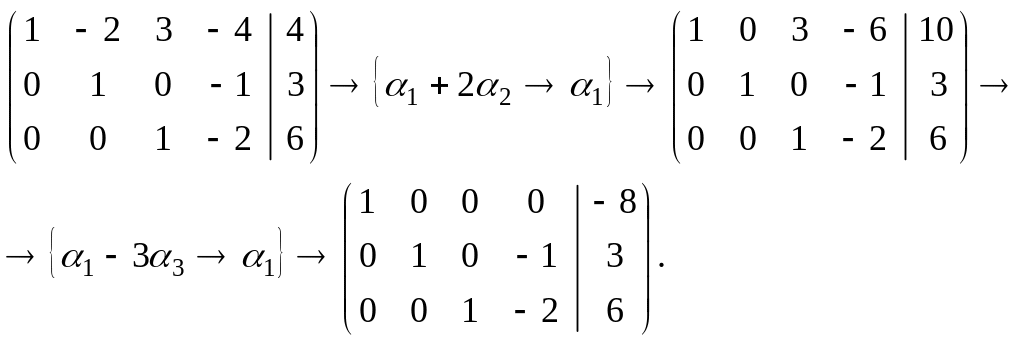
 .
.
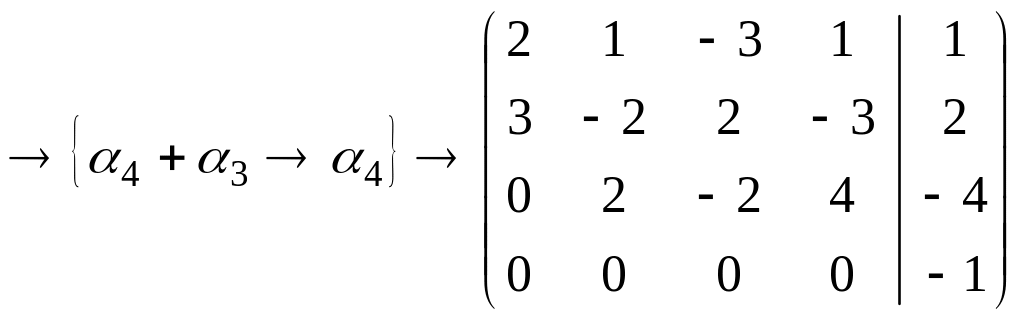 .
.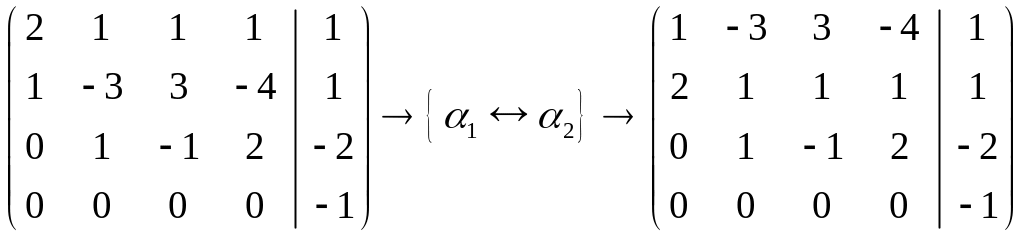 .
.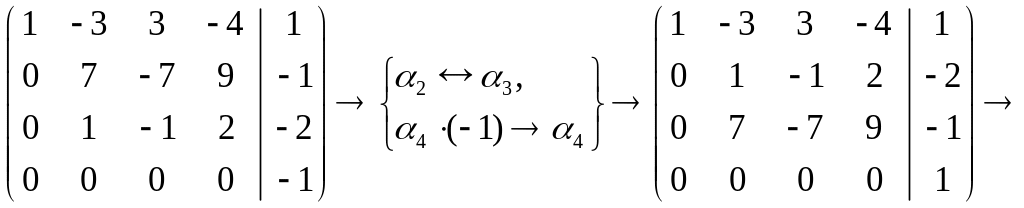
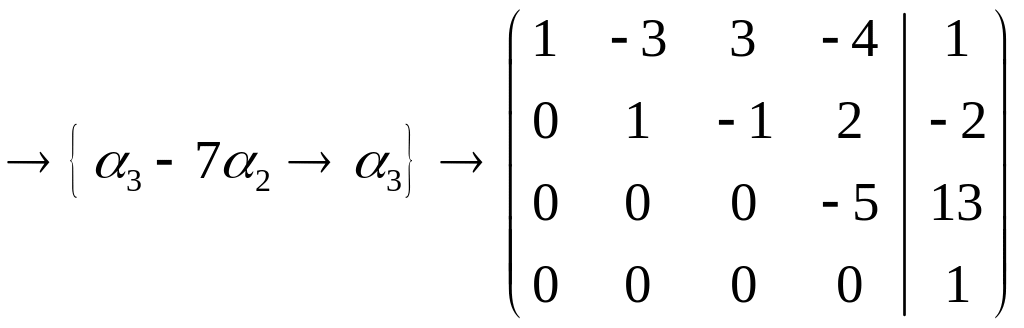 .
.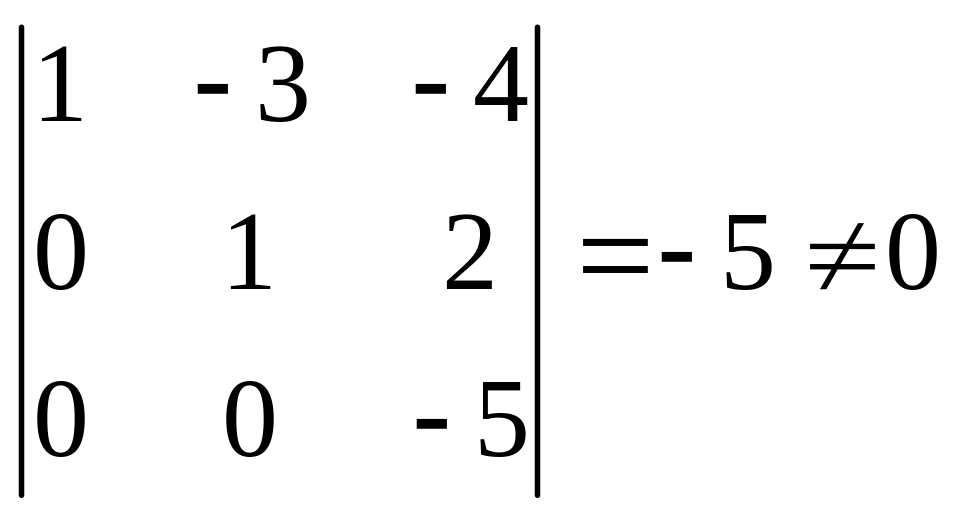
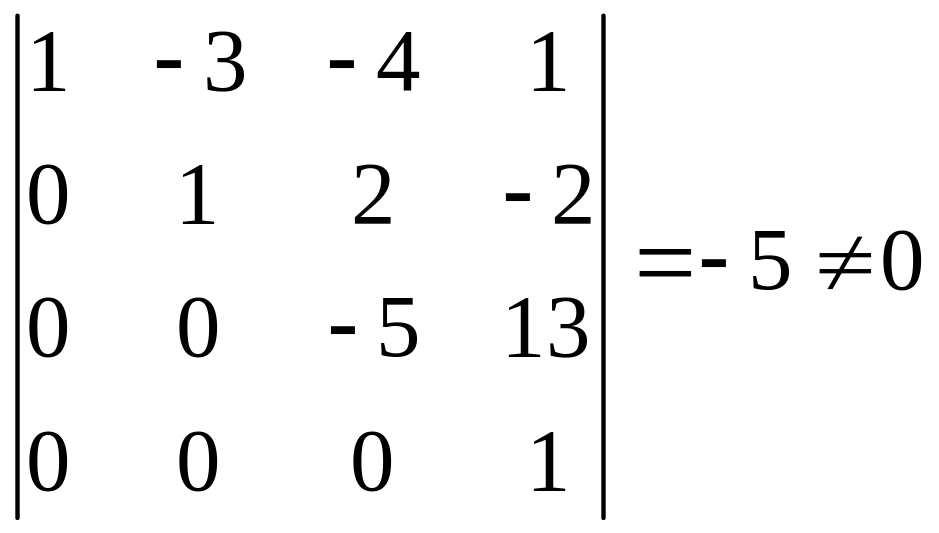
 и ответьте
на вопросы об этой системе.
и ответьте
на вопросы об этой системе.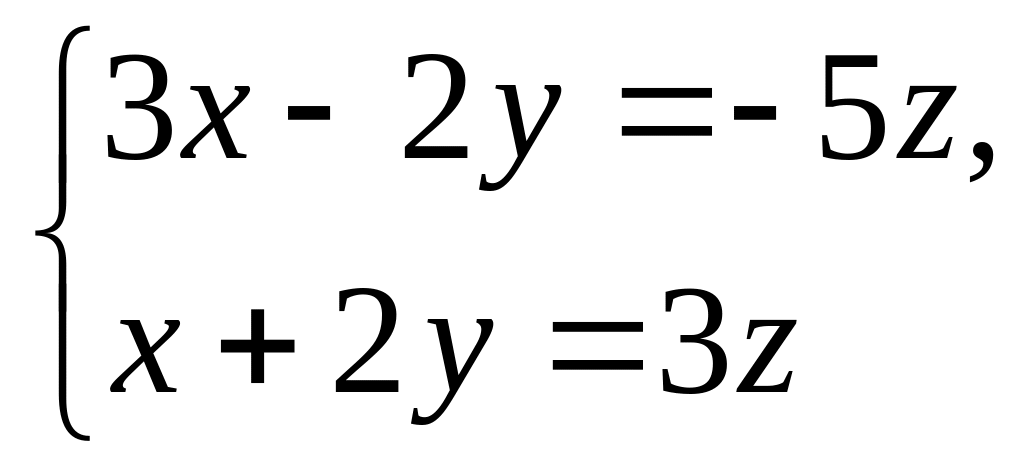 .
При
.
При
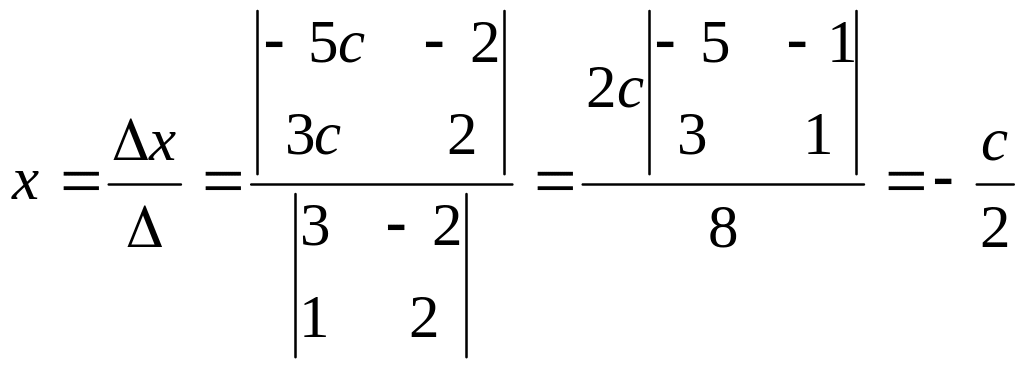 ,
,
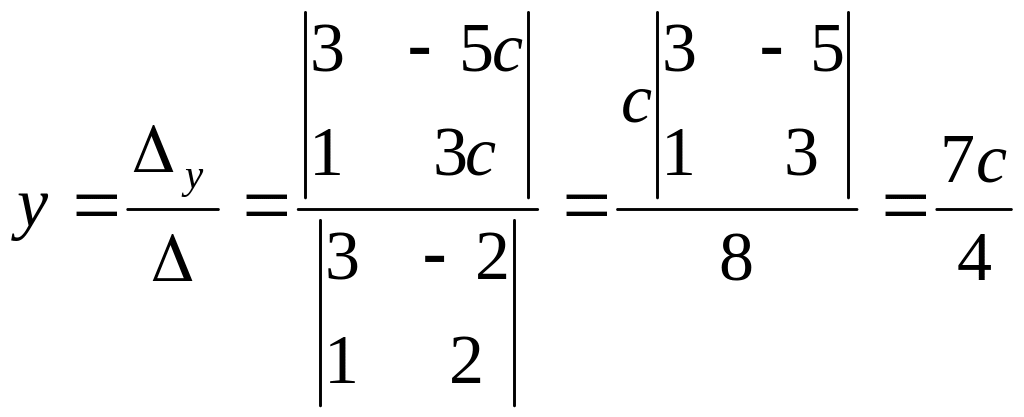 .
.
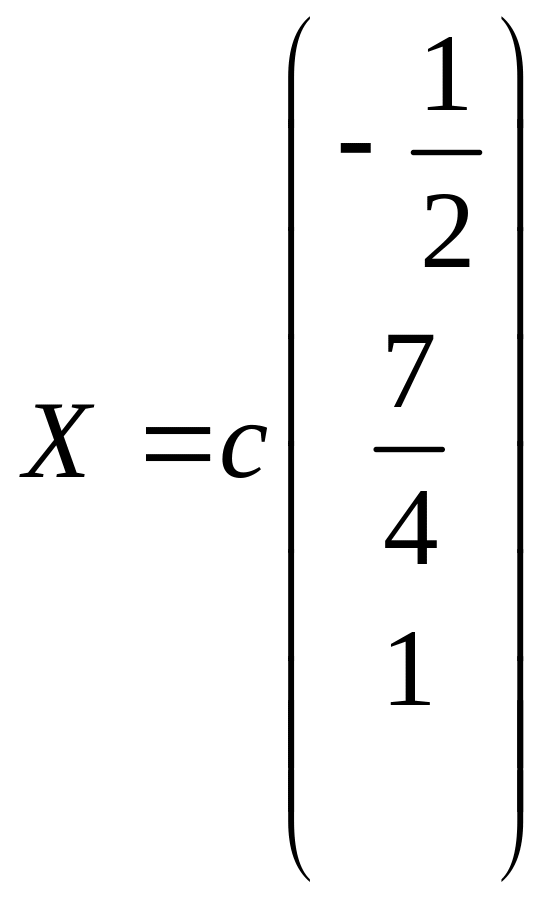
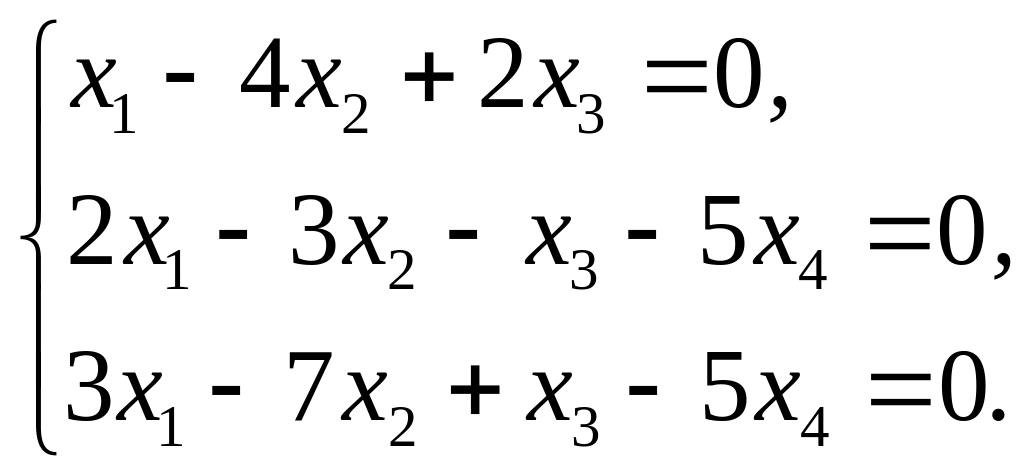

 .
.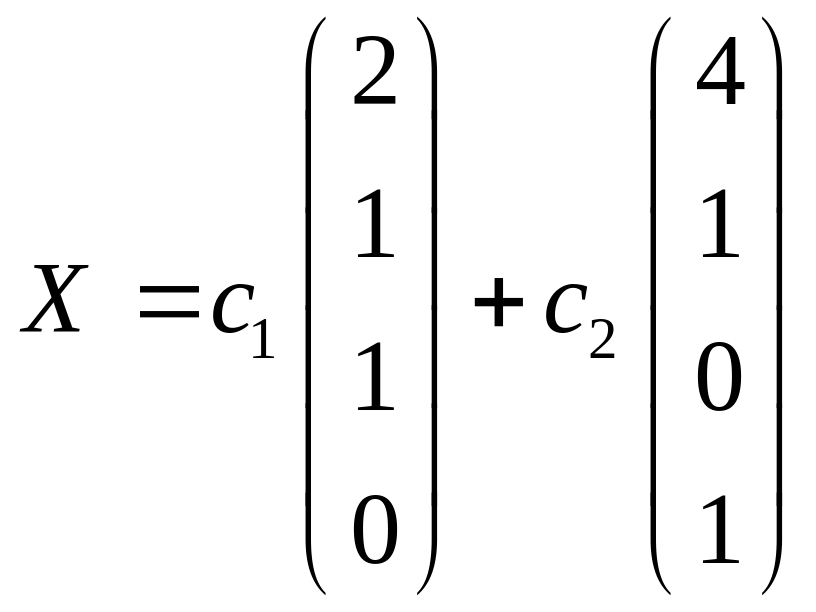 .
.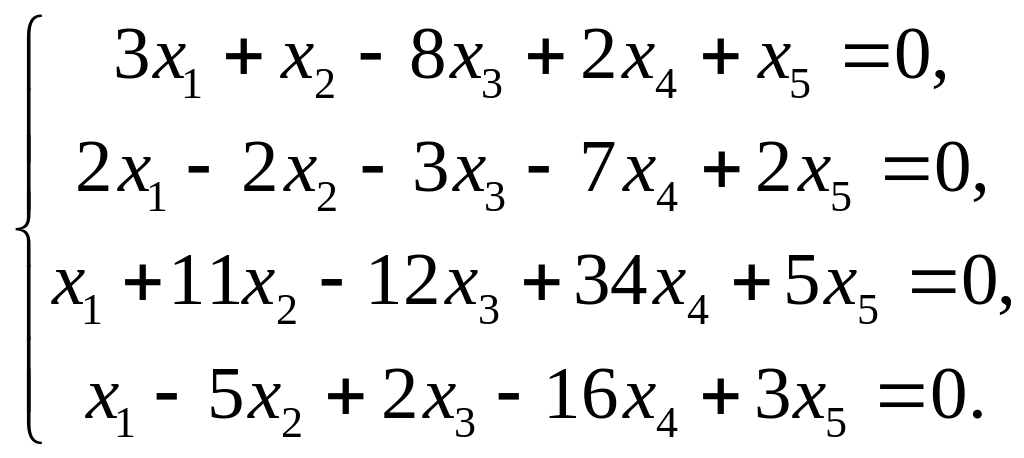

 .
.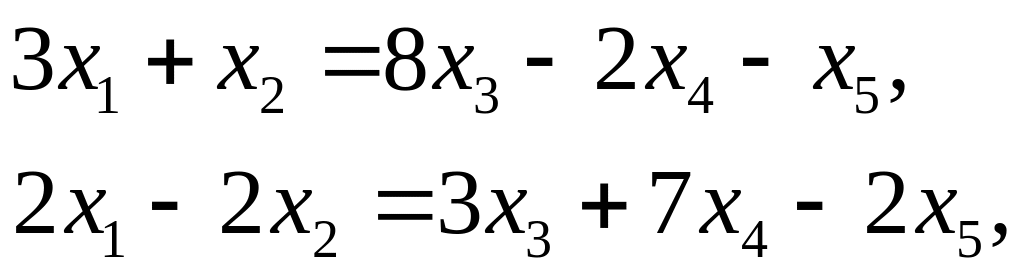
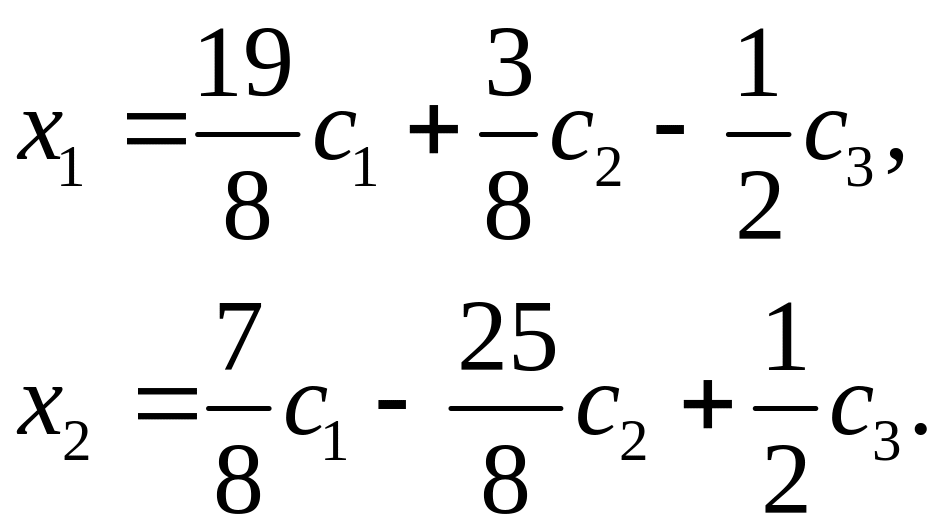
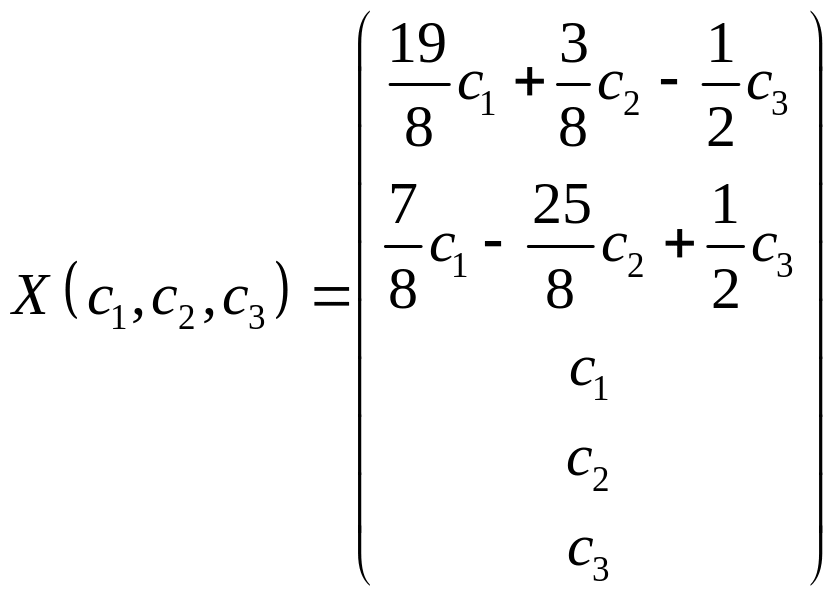
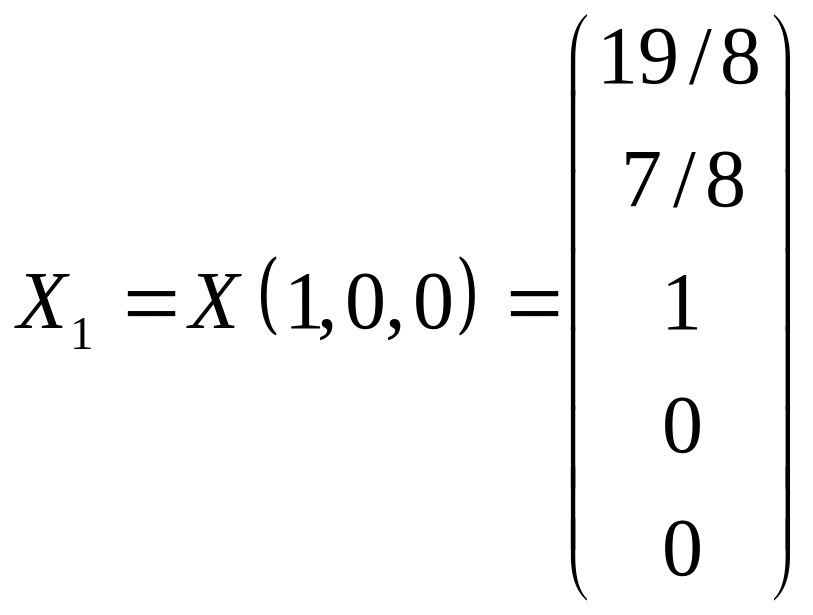 ,
,
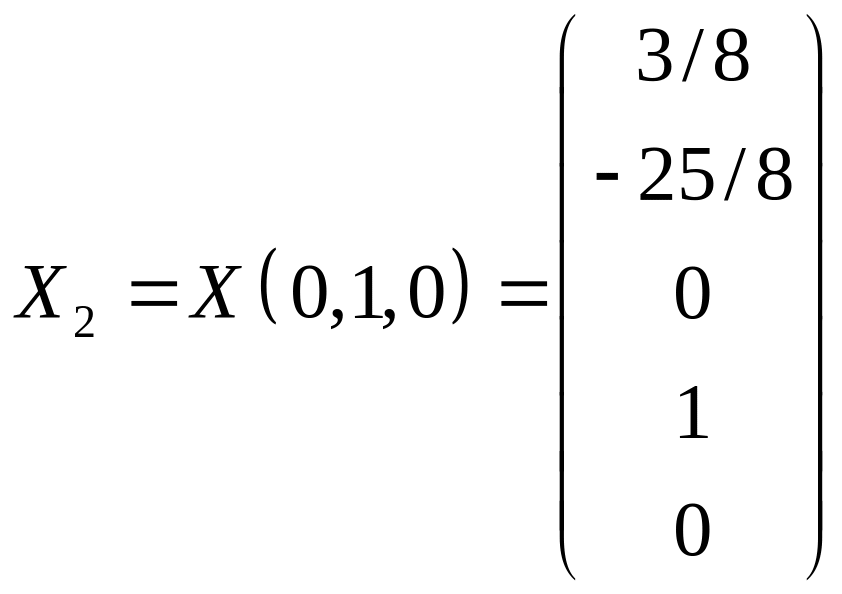 ,
,
 .
.