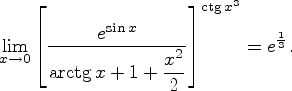- •3. Единственность предела сходящейся последовательности
- •4. Ограниченность сходящейся последовательности.
- •5. Сохранение знака сходящейся последовательности
- •10.Арифметические свойства сходящихся последовательностей.
- •11. Теорема Кантора о вложенных отрезках.
- •12.Теорема Больцано-Вейерштрасса об ограниченных последовательностях.
- •13. Критерий Коши сходимости последовательности.
- •14.Теорема о существовании точных границ числовых множеств.
- •15. Принцип Бореля-Лебега.
- •16.Теорема Больцано-Вейерштрасса о существовании предельной точки у ограниченного числового множества.
- •17. Эквивалентность двух определений предела функции в точке.
- •19.Критерий Коши предела функции в точке.
- •20.Непрерывность сложной функции.
- •21. Теоремы Вейерштрасса для непрерывных функций на отрезке.
- •22. Теорема Больцано-Коши о нулях функции.
- •25. Теорема о существовании обратной функции.
- •26. Теорема о существовании и непрерывности обратной функции.
- •29. Непрерывность дифференцируемой функции.
- •30. Производная и дифференцируемость функции в точке.
- •31. Дифференцируемость функции в точке: правила дифференцирования, дифференцируемость сложной функции.
- •33. Теоремы о среднем: Ферма, Ролля, Лагранжа, Коши.
- •35. Первое правило Лопиталя.
- •36. Теорема Тейлора.
- •37. Достаточные условия экстремума.
35. Первое правило Лопиталя.
Теорема
(Лопиталя). Пусть
функции ![]() и
и ![]() :
:![]() дифференцируемы
в выколотой окрестности
дифференцируемы
в выколотой окрестности ![]() точки
точки ![]()
![]()
![]()
![]()
![]() для
всех
для
всех ![]()
![]() существует
предел, конечный или бесконечный,
существует
предел, конечный или бесконечный, ![]() Тогда
существует и предел
Тогда
существует и предел ![]() и
имеет место равенство
и
имеет место равенство
![]()
Доказательство проведем
для случая ![]() Функции
Функции ![]() и
и ![]() непрерывны
на некотором интервале
непрерывны
на некотором интервале ![]() как
дифференцируемые на нем функции.
Доопределим функции
как
дифференцируемые на нем функции.
Доопределим функции ![]() и
и ![]() в
точке
в
точке ![]() :
: ![]() .
Таким образом, они становятся непрерывными
на отрезке
.
Таким образом, они становятся непрерывными
на отрезке ![]() .
Возьмем любое
.
Возьмем любое ![]() ,
тогда на отрезке
,
тогда на отрезке ![]() функции
функции ![]() и
и ![]() удовлетворяют
условиям теоремы Коши о среднем значении
( Пусть
функции
удовлетворяют
условиям теоремы Коши о среднем значении
( Пусть
функции ![]() и
и![]() : 1) непрерывны на отрезке
: 1) непрерывны на отрезке![]() 2) дифференцируемы
на интервале
2) дифференцируемы
на интервале![]() 3) производная
3) производная![]() во
всех точках интервала
во
всех точках интервала![]() . Тогда
существует такая точка
. Тогда
существует такая точка![]() ,
что имеет место
,
что имеет место ![]() ),
поэтому существует точка
),
поэтому существует точка![]() такая,
что
такая,
что ![]() Заметим,
что
Заметим,
что ![]() ,
иначе по теореме Ролля
,
иначе по теореме Ролля ![]() в
некоторой точке
в
некоторой точке ![]() .
Ясно, что и здесь
.
Ясно, что и здесь ![]() при
при ![]() .
Поэтому, по правилу вычисления предела
сложной функции, имеем
.
Поэтому, по правилу вычисления предела
сложной функции, имеем
![]()
Пример
1)
![]()
2)![]() 3)
3)![]()
36. Теорема Тейлора.
Формула
Тейлора для многочлена. Пусть
дан некоторый многочлен ![]() -й
степени (с действительными коэффициентами)
-й
степени (с действительными коэффициентами) ![]() .
Зададим произвольное
.
Зададим произвольное ![]() и
проведем преобразования, заменив
и
проведем преобразования, заменив ![]() на
на ![]() .
Получим
.
Получим
![]() Собрав
подобные члены при одинаковых степенях,
находим
Собрав
подобные члены при одинаковых степенях,
находим
![]() Это
есть разложение многочлена
Это
есть разложение многочлена ![]() по
степеням разности
по
степеням разности ![]() .
Дифференцируя его по
.
Дифференцируя его по ![]() ,
получим
,
получим
![]()
![]() Итак,
вычислены коэффициенты
Итак,
вычислены коэффициенты
![]() Следовательно,
многочлен
Следовательно,
многочлен ![]() можно
представить в виде
можно
представить в виде![]()
![]() Это
есть формула Тейлора для многочлена
Это
есть формула Тейлора для многочлена ![]() в
окрестности точки
в
окрестности точки ![]() .
. ![]() --
многочлен Тейлора степени
--
многочлен Тейлора степени ![]() от
функции
от
функции ![]() .
Если степень многочлена Тейлора
для
.
Если степень многочлена Тейлора
для ![]() есть
есть ![]() ,
то
,
то![]()
Пример. Разложим
многочлен ![]() по
степеням
по
степеням ![]() ,
т. е. в окрестности точки
,
т. е. в окрестности точки ![]() :
:![]() или
по-другому:
или
по-другому: ![]() Тогда
многочлен Тейлора степени
Тогда
многочлен Тейлора степени ![]() для
для ![]() есть
есть![]()
![]() Замечание. В
этом примере
Замечание. В
этом примере ![]()
![]()
![]()
Формула
Тейлора для произвольной функции. Если
у функции![]() существует
существует![]() ,
но функция
,
но функция ![]() не
есть многочлен, то для нее можно записать
многочлен Тейлора
не
есть многочлен, то для нее можно записать
многочлен Тейлора![]()
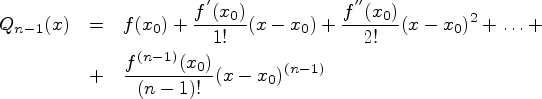 и
остаточный член
и
остаточный член ![]() ,
который,вообще говоря,не нуль.Равенство
,
который,вообще говоря,не нуль.Равенство![]() в
некоторой окрестности точки
в
некоторой окрестности точки ![]() называется формулой
Тейлора функции
называется формулой
Тейлора функции ![]() в
окрестности точки
в
окрестности точки ![]() ;
; ![]() --
многочлен Тейлора степени
--
многочлен Тейлора степени ![]() функции
функции ![]() ,
, ![]() --
-- ![]() -й
остаточный член формулы Тейлора.
-й
остаточный член формулы Тейлора.
Теорема
(Тейлора). Пусть
функция ![]() имеет
имеет ![]() -ю
производную в выколотой окрестности
точки
-ю
производную в выколотой окрестности
точки ![]() и
в самой точке
и
в самой точке ![]() имеет
непрерывную
имеет
непрерывную ![]() -ю
производную. Тогда
справедлива формула Тейлора
-ю
производную. Тогда
справедлива формула Тейлора![]() где
ее
где
ее ![]() -й
остаточный член
-й
остаточный член ![]() может
быть записан в форме Лагранжа:
может
быть записан в форме Лагранжа:![]() и
в форме Коши:
и
в форме Коши:![]() Доказательство проведем
для
Доказательство проведем
для ![]() Фиксируем
Фиксируем ![]() (см.
рис.).
(см.
рис.).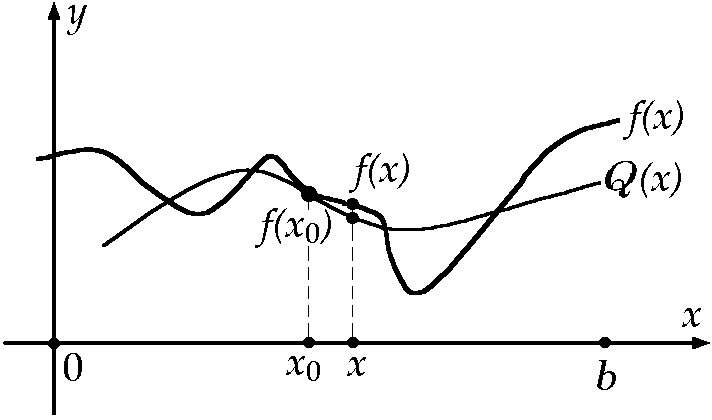
Запишем
формулу Тейлора функции ![]() :
:
![]()
![]() в
которой
в
которой ![]() --
остаточный член. Пусть
--
остаточный член. Пусть ![]() --
произвольное натуральное число.
Представим остаточный член в виде
--
произвольное натуральное число.
Представим остаточный член в виде![]() где
где ![]() -
неизвестно. Ясно, что
-
неизвестно. Ясно, что ![]() зависит
от
зависит
от ![]() Введем
новую переменную
Введем
новую переменную ![]() и
рассмотрим функцию
и
рассмотрим функцию![]()
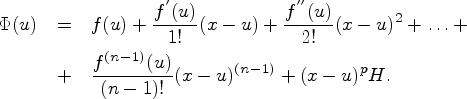 Функция
Функция ![]() обладает
следующими свойствами:1)
обладает
следующими свойствами:1) ![]() определена
и непрерывна на отрезке
определена
и непрерывна на отрезке ![]() ,
поскольку таковы функции
,
поскольку таковы функции ![]() на
отрезке
на
отрезке ![]() ;2)
;2) ![]() имеет
производную на интервале
имеет
производную на интервале ![]() ,
так как на нем имеет производную
,
так как на нем имеет производную ![]() -го
порядка функция
-го
порядка функция ![]() ;
3)
;
3)![]()
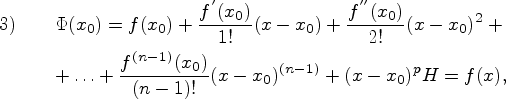 так
как имеет место формула Тейлора для
функции
так
как имеет место формула Тейлора для
функции ![]() .
Кроме того,
.
Кроме того, ![]() .Следовательно,
функция
.Следовательно,
функция ![]() удовлетворяет
на отрезке
удовлетворяет
на отрезке ![]() условиям
теоремы Ролля. Поэтому существует такая
промежуточная точка
условиям
теоремы Ролля. Поэтому существует такая
промежуточная точка ![]() ,
между точками
,
между точками ![]() и
и ![]() ,
что в ней
,
что в ней ![]() .Выпишем
производную
.Выпишем
производную ![]() после
всех сокращений и упрощений
после
всех сокращений и упрощений ![]() .
Так как
.
Так как ![]() ,
то получим уравнение
,
то получим уравнение ![]() Отсюда
найдем
Отсюда
найдем ![]() Следовательно,
с учетом того, что
Следовательно,
с учетом того, что ![]() остаточный
член запишется в виде
остаточный
член запишется в виде ![]() Получен
остаточный член в общей форме
Получен
остаточный член в общей форме![]() При
При ![]() получаем
остаточный член в форме Лагранжа, а
при
получаем
остаточный член в форме Лагранжа, а
при ![]() --
остаточный член в форме Коши.
--
остаточный член в форме Коши.
Замечание. 1. Формулу Тейлора можно записать в виде
![]()
![]()
![]()
![]() 2.
Формулу Тейлора функции
2.
Формулу Тейлора функции ![]() в
окрестности точки
в
окрестности точки ![]() :
:
![]()
![]()
![]()
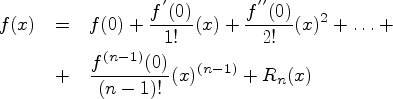 иногда
называют формулой Тейлора - Маклорена
функции
иногда
называют формулой Тейлора - Маклорена
функции ![]() .
Остаточные члены
.
Остаточные члены
 3.
Пусть функция
3.
Пусть функция ![]() имеет
в некоторой окрестности точки
имеет
в некоторой окрестности точки ![]() производную
производную ![]() -го
порядка, непрерывную в точке
-го
порядка, непрерывную в точке ![]() (следовательно,
производная
(следовательно,
производная ![]() -го
порядка непрерывна в окрестности
точки
-го
порядка непрерывна в окрестности
точки ![]() ).
Тогда справедлива формула Тейлора
функции
).
Тогда справедлива формула Тейлора
функции ![]() в
окрестности точки
в
окрестности точки ![]() с
остаточным членом в форме Лагранжа:
с
остаточным членом в форме Лагранжа:![]()
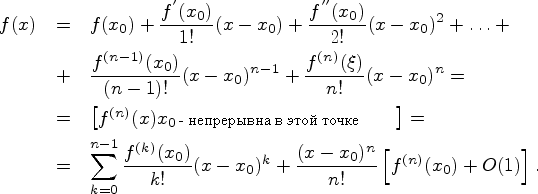
![]()
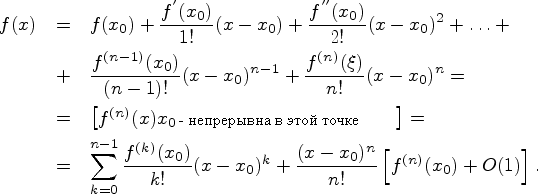 Таким
образом,
Таким
образом,![]()
![]()
![]() -
остаточный член в форме Пеано.
-
остаточный член в форме Пеано.
Формулы Тейлора основных элементарных функций
1. ![]() ,
, ![]() ,
, ![]() ,
, ![]() .Получим
формулу Тейлора с остаточным членом в
форме Лагранжа:
.Получим
формулу Тейлора с остаточным членом в
форме Лагранжа:![]() и
в форме Пеано:
и
в форме Пеано:![]()
Пример. Вычислим
число ![]() и
оценим погрешность вычисления:
и
оценим погрешность вычисления:![]()
![]()
Замечание. С
помощью формулы Тейлора можно вычислять
довольно точно значения функций и
оценивать величину ошибки, если остаточный
член берется в форме Лагранжа. Используя
формулу Тейлора с остаточным членом в
форме Пеано, такую оценку сделать
невозможно (из нее следует лишь,
что ![]() при
при ![]() и
при фиксированном
и
при фиксированном ![]() ).
2.
).
2. ![]() и
т. д.,
и
т. д., ![]() Следовательно,
получим формулу Тейлора - Маклорена:
Следовательно,
получим формулу Тейлора - Маклорена:![]()
![]()
![]() для
любых фиксированных
для
любых фиксированных ![]() .
Но особенно быстро остаточный член
стремится к
.
Но особенно быстро остаточный член
стремится к ![]() при
при ![]() .
.
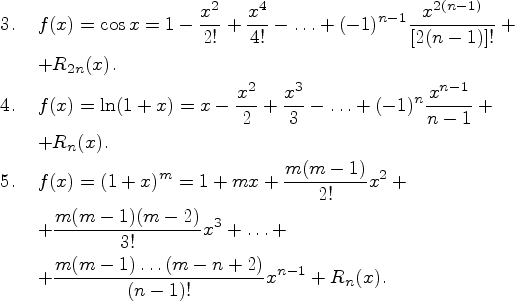
![]()
![]()
![]()
![]()
![]()
![]()
![]() В
частном случае
В
частном случае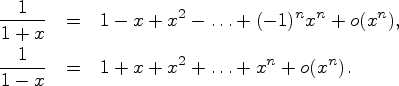
![]()
Пример.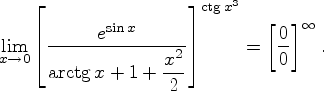 Необходимо
рассмотреть
Необходимо
рассмотреть
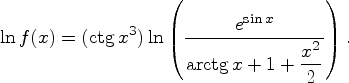 Здесь
понадобится формула Тейлора
Здесь
понадобится формула Тейлора ![]()
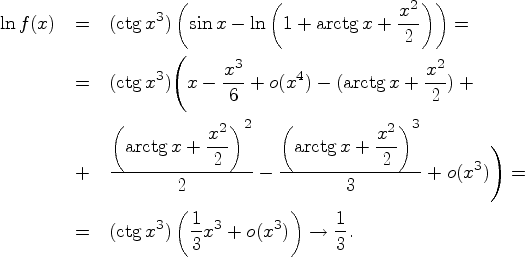
![]()
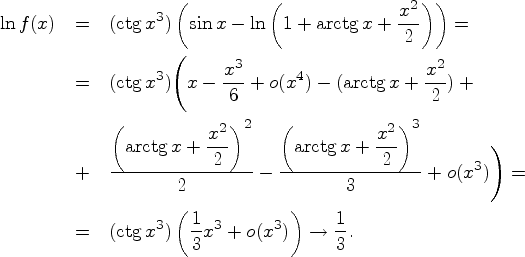
![]()
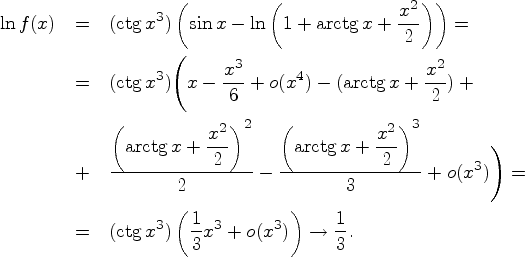
![]() Следовательно,
Следовательно,