31. Дифференцируемость функции в точке: правила дифференцирования, дифференцируемость сложной функции.

Свойства производной. Пусть функции иимеют производные в точке. Тогда существуют производные в левых частях следующих равенств и имеют место соотношения:1)2)3).

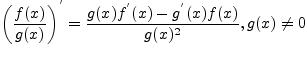Докажем, например, свойство 2. Рассмотрим

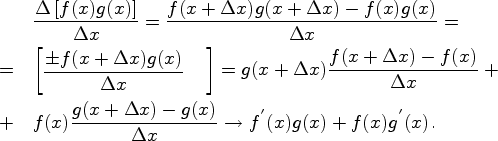
Производные элементарных функций 1) 2); 3); 4).

Доказательство

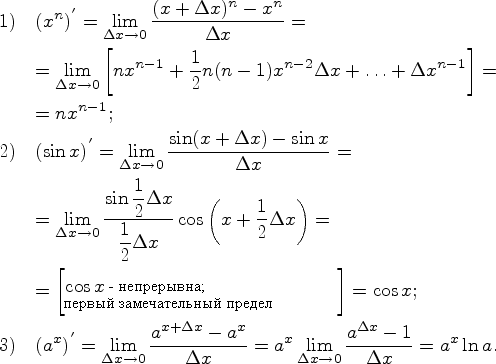
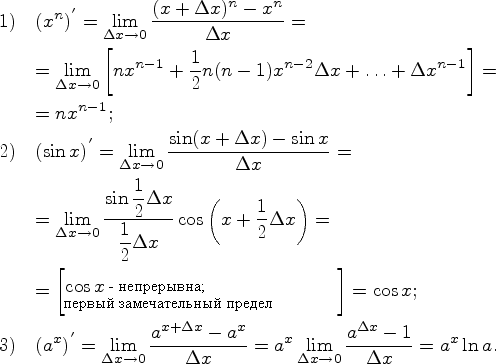
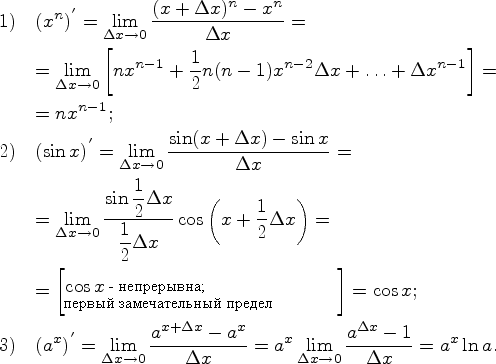
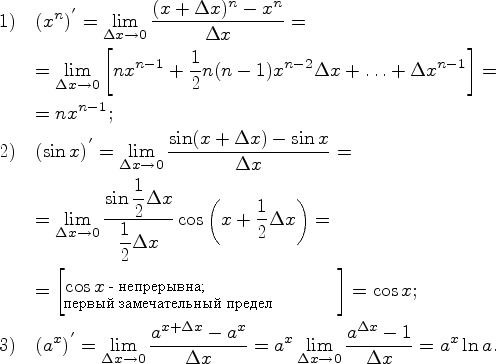
Дифференциал функции в точке обладает важными свойствами. Пусть функции идифференцируемы в точке, тогда имеют место равенства

Доказательства этих свойств легко следуют из определения и свойств производных.

Пример.

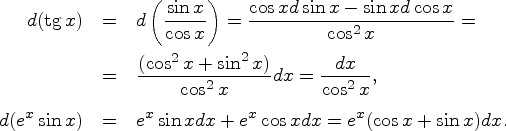
Производная сложной функции Теперь можно установить важное в практических приложениях правило, позволяющее вычислить производную сложной функции, если известны производные составляющих ее функций.

Теорема. Пусть задана сложная функция ; функция имеет производную в точке , а функция имеет производную в точке  Тогда функция имеет производную в точке и 

Доказательство. Так как функция дифференцируема в точке , то  где при . Если положить , то функция непрерывна в точке . Придадим переменной в точке малое приращение ; оно влечет приращение зависимой переменной :. Итак,Разделив на , получим Так как существует , то функция непрерывна в точке и, следовательно, при (Если функция имеет производную в точке то она непрерывна в этой точке.), и так как , то функция непрерывна в точке . Отсюда сложная функция, как суперпозиция непрерывных функций , непрерывна в точке . Теперь, переходя к пределу при , получим 

Пример. Тогда 

Замечание. Из теоремы следует инвариантность формы первого дифференциала.

Если задана функция от функциито дифференциал зависимой переменной равен произведению производной от нее по одной из переменных или на дифференциал по этой переменной, причем неважно, зависимая эта переменная или нет. Действительно, 

Пример. Найдем дифференциал функции :

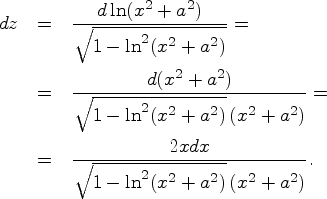
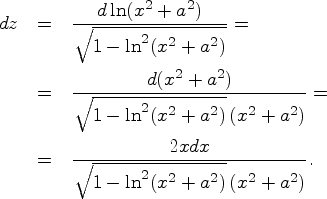
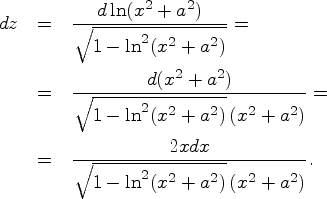
33. Теоремы о среднем: Ферма, Ролля, Лагранжа, Коши.

Теорема (Ферма). Если функция определена на интервале, в точкепринимает наибольшее значение и производнаясуществует, то

Доказательство. По условию теоремы для всех выполняется неравенство. Тогда (см. рис.)(1)(2). Так как существует производнаято существуют и односторонние производные, и они равны производной. Поэтому из (1) следует, а из (2) следует. Отсюда имеем

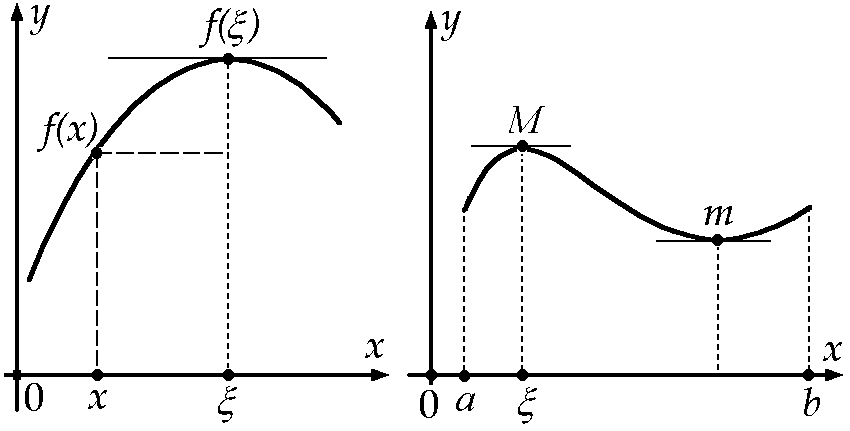
Теорема (Ролля). Пусть функция : непрерывна на отрезке имеет в каждой точке интервала производную; имеет на концах отрезка равные значения: . Тогда существует точка такая, что .

Доказательство. По второй теореме Вейерштрасса (Непрерывная функция на отрезкедостигает в некоторых точках отрезкасвоих точных верхней и нижней границ, т. е. существуюттакие, что) непрерывная функция на отрезке принимает наибольшее и наименьшее значения в некоторых точках отрезка (см. рис.). ПустьЕсли , то , поэтому на .Если , т. е. , то из условия следует, что одно из значений, или , функцией не принимается на концах отрезка , а принимается внутри интервала . Пусть, для определенности, значение принимается внутри интервала , т. е. существует точка такая, что  Так как производная функции существует в точке , то по теореме Ферма (см.выше) .

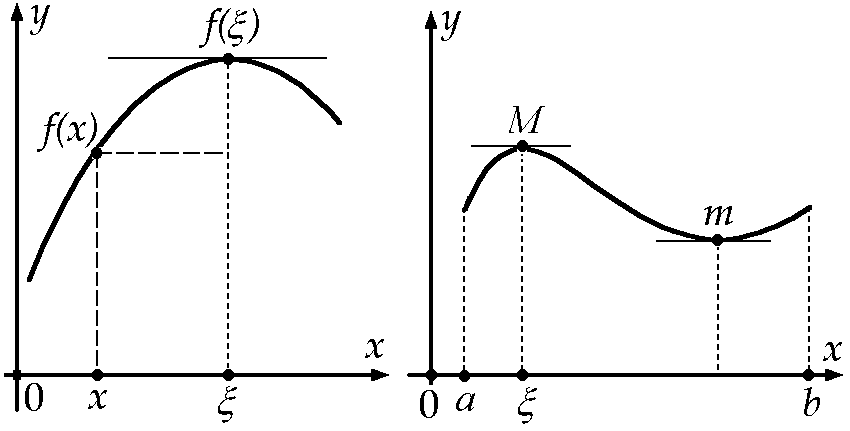
Теорема (Лагранжа). Пусть функция непрерывна на отрезке и имеет производную в каждой точке интервала . Тогда существует точка такая, что (см. рис.).

Доказательство. Рассмотрим функцию , где параметр выберем так, чтобы , т. е.. Отсюда Для функции выполнены все условия теоремы Ролля (см.выще):1) непрерывна на ; 2)существует в ; 3) .Тогда по теореме Ролля существует такая, что , т. е. . Следовательно, 

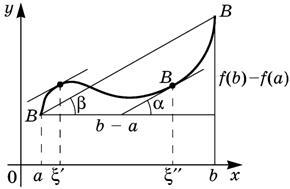
Замечание. При , т. е., получаем формулуконечных приращений Лагранжаили

Следствие. Пусть функция :непрерывна надифференцируема насуществует, конечный или нет. Тогда существует правая производная, конечная или нет, и.

Напомним, что , если функциянепрерывна в точкесправа и существует

Доказательство. Пусть . Возьмем любое , тогда по теореме Лагранжа (см. выше), примененной к отрезку , существует точка такая, что выполняется равенство .Точка будет зависеть от , т. е. выбирается какое-то одно значение в . Итак, . Отсюда следует, что при . Следовательно, определена сложная функция  и 

По правилу вычисления предела сложной функции имеем 

Следовательно, 

Пример. , вычислим,,:

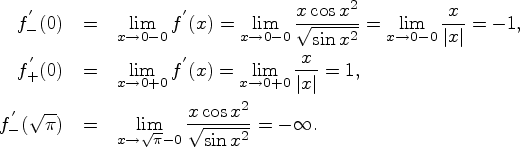
Теорема (Коши). Пусть функции и : непрерывны на отрезке 

 дифференцируемы на интервале производная во всех точках интервала . Тогда существует такая точка , что имеет место 

Доказательство. , иначе по теореме Ролля (см. выше) для функции существует точка такая, что . Рассмотрим функцию. Параметр подберем так, чтобы :следовательно,Итак, функция удовлетворяет всем условиям теоремы Ролля, поэтому существует точка такая, что . Отсюда и