29. Непрерывность дифференцируемой функции.

Функция называетсянепрерывной в точке , если существует предел функциипри, и он равен ее значению в точке, т. е.Можно записать развернутое определение непрерывности функции в точке, если воспользоваться определением предела функции по Коши или Гейне. Функцияназываетсянепрерывной в точке по Коши, если она определена в и для любогосуществуеттакое, что для всехивыполняется неравенство.  Функцияназывается непрерывной в точке по Гейне, если она определена в и для любой последовательноститакой, что, выполняется .

Теорема. Если функция имеет производную в точкето она непрерывна в этой точке.

Доказательство. Из существования следует, что разностьесть бесконечно малая функция при. Отсюдаи, следовательно, приращение функцииесть бесконечно малая функция при. Отсюдат.е., что означает непрерывность функциив точке.

Пример. Функция непрерывна в точке, но производная в точкене существует, так как не существует предел.

Из непрерывности в данной точке не следует дифференцируемость в этой точке

30. Производная и дифференцируемость функции в точке.

Производная: Важной характеристикой движения материальной точки является ее мгновенная скорость. Допустим, материальная точка движется по закону по прямой, т. е. находится в свободном падении под действием постоянной силы тяжести. Фиксируя произвольный момент времении какое угодно егоприращение , получимсреднюю скорость на отрезке времени Для нашего закона движенияСредняя скорость непостоянна, она зависит от момента времении от приращения времени.Мгновенной скоростью (или просто скоростью) движущейся точки называется предел, к которому стремится средняя скоростьпри стремлении к нулю приращения времени, т. е.Итак, при нахождении скорости изменения какой-то переменной величиныв точкенам нужно совершить предельный переход

Число , если такой предел существует, называется производной функциив точке.

Задача о проведении касательной к графику функции в точкетоже приводит к необходимости совершить подобного рода предельный переход. Рассмотрим квадратичную функциюи ее график. Проведем касательную к этой кривой в точке.Касательной к кривой в точке называется предельное положение секущей(если оно существует) при стремлении точкивдоль кривой к точке(см. рис.). Придадим абсциссеприращение, получим соответствующее приращение функциии тангенс угла наклона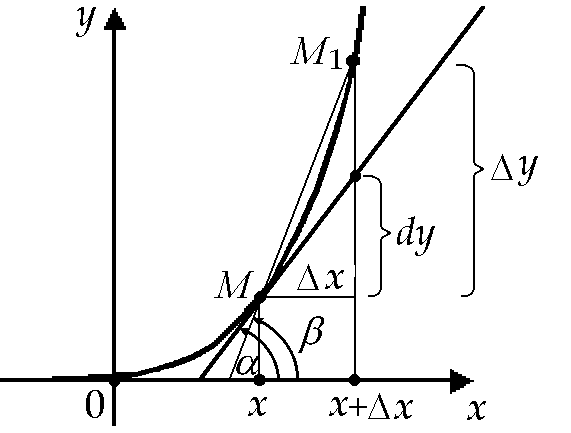

секущей :В нашем случае. Предельное положение секущей существует при, и тангенс угла наклона ее есть

Дифференцируемость: Рассмотрим приращение функции в точке

Поведение этого приращения, как функции приращения аргумента при фиксированном, показывает, существует ли производная в этой точке у функции. В случае существования производнойприращениеможет быть записано в виде (т.к.Если функция имеет производную в точке то она непрерывна в этой точке)Если же приращение функциив точкеможет быть записано в виде то функция называется дифференцируемой в точке . Докажем, что если функция имеет производную в точке, то она дифференцируема в ней.

Теорема. Функция имеет производную в точкетогда и только тогда, когда она дифференцируема в этой точке.

Доказательство. Необходимость доказана выше. Достаточность. Рассмотрим  . По определениюимеемОтсюда следует, что при наличии дифференцируемости функциив точкеглавную роль в приращениииграетлинейная часть . Она называетсядифференциалом функции в точкеи обозначаетсяЗдесь

Замечание. Если функция задана в виде , то и приращение ее, и дифференциал можно записать так:

Пример.