17. Эквивалентность двух определений предела функции в точке.

Соответствие между элементами множествиназываетсяфункцией, еслилюбомуэлементупоставлен в соответствиеединственныйэлемент(это записывается следующим образом:или).

Определение предела функции по Гейне.Пусть в каждой точке интервала, кроме, быть может, точки, определена функцияЧислоназываетсяпределомфункциипри стремлениик, если для любой последовательноститакой, чтопоследовательностьзначений функциисходится кпри.В этом случае пишут

Пример. Пусть

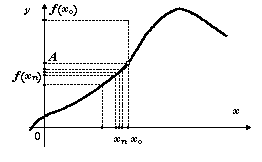
Предел функции прине существует, так как длязначения функции, а для,

.

Пример.ПустьТогдатак как

Определение предела функции по Коши.Пусть в каждой точке интервала, кроме, быть может, точки, определена функция. Числоназываетсяпределомфункциипри стремлениик, если для любогосуществуеттакое, что для всех, удовлетворяющих условию, выполняется неравенство. Или, на формальном языке,

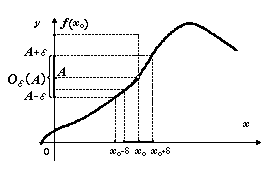
Теорема.Определения предела функции по Гейне и по Коши эквивалентны

Доказательство.

Необходимость. Докажем от противного. Пусть по Гейне, но не по Коши, т. е.Пусть. Тогда найдутсяи. Отсюда, и посвойству (Если для всех n и ,то) . Поэтому, по определению Гейне, , но по построению последовательностьлежит вне окрестности, что противоречит тому, что.

Достаточность.Пусть(по Коши). Согласно определению Гейне, возьмем любую последовательность. Для доказательства того, что, возьмем любое. Тогда из определения предела по Коши найдется соответствующее. Для, в силу сходимости, найдется номертакой, что для всех, но тогда по определению Коши, что доказывает, что, т. е.(по Гейне).

Пример 5.2.3.Докажем, что по определению КошиВозьмем произвольное, рассмотрим левую часть основного неравенства в определении КошипоэтомуИскомое. ЗдесьиДействительно, пусть для всехвыполняется, тогда, поэтому

19.Критерий Коши предела функции в точке.

Говорят, что функция удовлетворяетусловию Кошив точке, если она определена в, быть может, кроме самой точки, и выполнено:Теорема.Для того чтобы существовал конечный предел необходимо и достаточно, чтобы в точкевыполнялось условие Коши для функции

Доказательство.Необходимость. Легко следует из определения предела по Коши(

). Действительно, возьмем любое , тогда длянайдется.Возьмем любые, тогда

Достаточность. Пусть выполняется условие Коши (см. выше). Докажем, что существует (по Гейне). Пусть дана любая последовательностьВозьмем любое, по нему найдемиз условия Коши, тогда существует номертакой, что для всех, а следовательно, снова поусловию Коши, выполняется неравенство . Отсюдафундаментальна (см. критерий Коши сходимости последовательностей), значит, последовательностьсходится к некоторому числу.Остается доказать, что и для другой последовательности. Действительно, по изложенному выше существуетпри. Рассмотрев третью последовательностьбудем иметь. Следовательно,

20.Непрерывность сложной функции.

Теорема.Если функция непрерывна в точке, а функциянепрерывна в точке, где, то сложная функциянепрерывна в точке.

Доказательство.Пусть. Тогда в силу непрерывности в точкефункциипоследовательностьсходится к. Но тогда, в силу непрерывности уже функциив точке,последовательностьсходится к. Итак, из определения Гейне следует, что функциянепрерывна в точке.

Замечание.Если считать, что существуют пределыприипри, то в теореме доказано, что

Это равенство можно понимать как правило замены переменнойпри нахождении пределов.

Пример.