MatAn_thory

Запишем формулу Тейлора для некоторых элементарных функций при x0 0.

1).

Пусть f (x) ex и

x

0.

Вычислим производные функции ex

в точке x и

0

в точке x :

f n (x) ex,

f n (0) 1. Используя формулы (8.5) и (8.6), получим:

0

ex 1

x

x2

...

xn

o xn .

(8.9)

1!

2!

n!

В частности, при n 1

и

n 2 имеем:

x2

ex 1 x o(x),

ex 1 x

o(x2).

2

2).

Пусть

f (x) sin x

и x0

0. Ранее было показано, что

f n (x) sin

n x

.

Тогда

f n (0) sin

n

0,

n 2k

k 1

,n 2k 1.

2

2

( 1)

Используя формулы (8.5) и (8.6) при n=2k, получим:

sin x x

x3

x5

... ( 1)k 1

x2k 1

o(x2k )

.

(8.10)

2k 1

!

3!

5!

x3

В частности, при k 1 и k 2 имеем:

sin x x o(x2),

sin x x

o(x4).

3!

f x

3).

Пусть

f (x) cosx

и x0 0. Представим

в виде cosx sin

x .

2

n

n

0,

n

Тогда

f n (x) sin

x

и

f n (0) sin

k

2

( 1)

, n

2

2

2

Используя формулы (8.5) и (8.6)

при n 2k 1,

получим:

cosx 1

x2

x4

... ( 1)k

x2k

o(x2k 1)

.

2!

2k !

4!

2k 1

2k.

(8.11)

В частности, при k 1 имеем:

cosx 1

x2

o(x3).

2

4). Пусть f (x) ln(1 x)

и

x0 0. Вычислим производные этой функции в

точке x

и в точке x0

0:

1

1

2

4

2 3

1 x,

1 x 3

1 x 4

f (x)

f (x) 1 x 2

,

f

(x)

,

f

(x)

,...

f

1,

f

f

4

(0) 3!,..., f

n

(0) 1

n 1

n 1 !

(0) 1,

f (0)

(0) 2!,

Тогда

f n 0

1 n 1 n 1

!

1 n 1 1 2 3 ... n 1

1 n 1

.

n!

n!

n

1 2 3 ... n 1 n

Используя формулы (8.5) и (8.6), получим:

ln 1 x x

x2

x3

... ( 1)n 1

xn

o(xn)

.

(8.12)

3

2

n

В частности, при n 1 имеем:

ln 1 x

x o(x).

(8.13)

41

5). Пусть		x0 0	и – действительное число. Тогда
	f (x) 1 x ,

f		x		1	,	f			2	,	f
			1 x					(x) 1 1 x				(x)
f			f									,...,
	(0) ,			(0) 1 , f					(0) 1 2

Используя формулы (8.5) и (8.6), получим:

3	, ;
1 2 1 x

f n 0 1 n 1 .

1 x 1 x

1

x2 ...

1 ... n 1

xn o(xn).

2!

n!

В частности, при n 1 и при n 2 имеем:

1 x o(x),

(8.14)

1 x

1 x a 1 ax

a a 1

x2 o

x2

.

(8.15)

f (x) a x n,

2!

6). Пусть

n –натуральное число. Тогда

n 1

, f

1 a x

n 2

, , f

n

x n

n 1 2 1 a x

n n

n!.

f (x) n a x

(x) n n

f n 1

c

Так как f n

1 (x) 0, то остаточный член

R (x)

xn 1 равен нулю.

n

n 1 !

Учитывая, что

f

n 1

,

1 a

n 2

,... ,

f

n

(0) n!,

из формулы

(0) na

f (0) n n

(8.5) получим:

a x n an

n

an 1x

n n 1

an 2x2

... xn

.

(8.16)

1!

2!

Эту формулу называют «бином Ньютона».

Пример 8.4.

Вычислить число е

с точностью 0,01.

x2

xn

Решение. Воспользуемся формулой (8.9): ex 1

x

...

R x

.

1!

2!

n!

n

При x 1 эта формула примет вид:

e1

1

1

1

...

1

R

1 .

n!

Запишем остаточный член Rn x

1!

2!

n

в форме Лагранжа по формуле (8.8), учитывая,

что x 0, f n 1

(x) ex :

0

R

n

(x)

f n 1 (c)

(x x )n 1

ec

xn 1,

R

n

1

ec

,

n 1 !

0

n 1 !

n 1 !

причем точка c

находится между x 1

и x 0,

то есть

0 c 1. Тогда

ec e1

3.

0

Подберем

n

так,

чтобы

R

n

1 0,01.

Так

как

R

n

(1)

ec

3

0.01,

то

n 1 !

n 1 !

n 1 ! 300.

Это неравенство выполняется при n 5, так как

4! 1 2 3 4 24,

5! 24 5 120,

6! 120 6 720.

Итак, с погрешностью 0,01

e 1

1

1

1

1

1

2

1

1

1

1

2,72.

120

1!

2!

3!

4!

5!

2

6

24

Формулу Тейлора иногда удобно использовать для отыскания пределов.

42

Пример 8.5. Найти: lim

cosx e x2 /2

.

x 0

x4

0

Решение. Имеем неопределенность

. Для ее раскрытия воспользуемся

0

формулами (8.11) при k 2 и формулой

(8.9) при n 2, причем в формуле (8.9)

заменим x на

x2

:

2

x2

x4

x2

x4

cosx 1

o(x4) 1

o

x4 ,

2!

4!

2

24

x2

2

2

x2

1

x2

x2

x2

x4

e 2 1

o

1

o

x4

.

2!

2

2

8

2

2

Учитывая эти разложения, вычислим предел:

		x2				x	2		x	4			x	2		x	4				x4	o x
				1							o(x	4) 1						o(x4)					4
	cosx e	2	2 24										2		8						12					1
lim				lim															lim								.
	x4											x4										x4				12
x 0				x 0															x 0

9. Исследование функций с помощью производной

Одним из приложений производной является применение производной к исследованию функции и построению графика функции. Мы рассмотрим такие характеристики функции, как монотонность, экстремум, выпуклость, а также асимптоты графика функции.

9.1.Монотонность функции

Кмонотонным функциям относятся функции, возрастающие или убывающие на промежутке. Напомним, что функция возрастает (соответственно убывает) на интервале a,b , если для любых точек x1, x2 из этого интервала из нера-

венства x1 x2 следует неравенство f x1 f x2 (соответственно f x1 f x2 ).

	Теорема 9.1 (критерий монотонности).
	Дифференцируемая функция f x			возрастает (соответственно убывает) на ин-
	тервале a,b	тогда и только тогда, когда			f x 0 (соответственно			f x 0) на
	интервале a,b .
	Доказательство. 1). Пусть функция			f x	возрастает на a,b .
	Если x 0,	то f x x f x ,	f x f x x f x 0			и	f x	0.
							x
	Если x 0,	то f x x f x ,	f x f x x f x 0			и	f x	0.
							x

43

	Таким образом,			f x	0 и для x 0, и для x 0. Тогда			f x lim		f x	0,
				x						x
									x 0
	причем x произвольная точка из интервала a,b .
	2). В обратную сторону, пусть f x 0 на интервале a,b . Применим тео-
	рему Лагранжа к функции f x на произвольном отрезке
				f x2 f x1 f c x2 x1 ,		c x1,x2 a,b :
					f x2 f x1 f c x2 x1 ,		c x1,x2 .
	Так как	f c 0,		x2 x1 0 , то f x2 f x1 0. Таким образом,					f x1 f x2
	для произвольных точек x1, x2 из a,b таких, что x1						x2 ; значит, функция f x
	возрастает на a,b .
					9.2. Экстремумы функции
	Пусть функция f x непрерывна на интервале a,b , содержащем точку x0 .
	Напомним ряд определений.
	1). Точка x0		называется точкой максимума функции f x					, если	f x0 f x
	для всех	x	из некоторой выколотой окрестности точки x0 .
	2). Точка x0		называется точкой минимума функции f x					, если	f x0 f x
	для всех	x	из некоторой выколотой окрестности точки x0 .

3). Точки максимума и минимума функции называют точками экстремума функции.

Так как f x f x0 f x0 , то в окрестности точки x0 y

f x0 0, если x0 точка максимума;

f x0 0, если x0 точка минимума.

	На рис.21 точка максимума x1, точка минимума x2 .						o	x1	x
	Для отыскания точек экстремума выведем необходи-								x
									2
	мое условие экстремума и достаточные условия.								Рис.21
	Теорема 9.2 (необходимое условие экстремума).
	Пусть функция f x имеет экстремум в точке x0 .					Тогда производная f x в
	точке x0 равна нулю или не существует.
	Доказательство от противного. Пусть производная					f x	в точке x0		существует
	и не равна нулю, например, f x0		0. Тогда	lim	f x0		f x0 0		и из свой-
						x
		f x0	x 0
	ства пределов следует, что		0 в некоторой окрестности точки x . Поэто-
		x							0
	му f x0 0, если x 0, и f x0 0, если x 0. Так как f x0							меняет знак в
	окрестности точки x0 , то экстремума в точке x0			функция не имеет, что противо-
	речит условию теоремы.		44

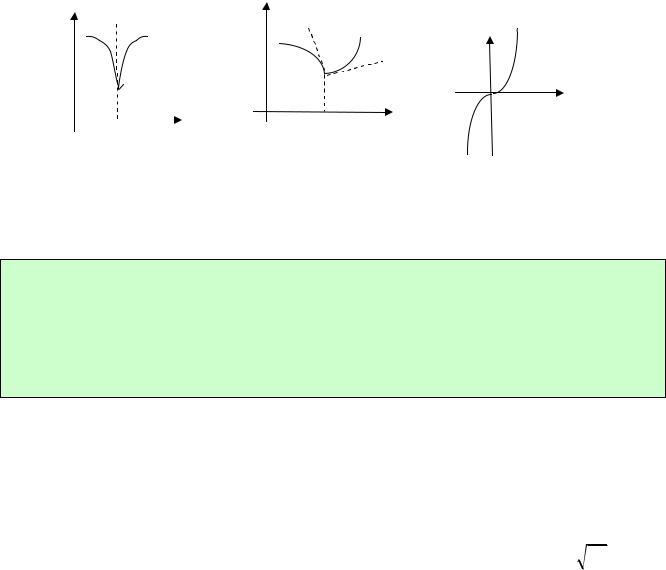
Сделаем ряд замечаний.

1). Точки экстремума, в которых f x 0, назовем точками гладкого экстрему-

ма. В таких точках касательная к графику функции параллельна оси ox (рис.21).

2). Точки экстремума, в которых f x не существует, назовем точками острого

экстремума. В таких точках касательная к графику функции перпендикулярна оси ox(рис.22) или не существует (рис.23).

3). Точки, в которых производная функции равна нулю или не существует,

называют критическими точками функции.

4). Необходимый признак экстремума не является достаточным, то есть из того,

что f x0	равна нулю или не существует,				не следует, что	f x имеет экстремум
в точке x0 . Например, для функции				y x3	ее производная y 3x2 равна нулю
при x 0, но x 0 (рис.24) не является точкой экстремума функции.
y	T		y	l2
		M
						y
					l	y x3
					1
	M0			M0		o	x
			o
		x			x
o	x			x0
	0
	Рис.22			Рис.23		Рис.24

Для исследования критической точки на экстремум используют первое или второе достаточное условие экстремума.

Теорема 9.3 (первое достаточное условие экстремума).

Пусть функция f x непрерывна в окрестности критической точки x0 и диффе-

ренцируема в выколотой окрестности точки x0 . Если производная f x при пе-

реходе (слева направо) через точку x0 меняет знак с плюса на минус, то x0 есть точка максимума; если с минуса на плюс, то x0 точка минимума.

Доказательство. Пусть f x		при переходе через точку x0 меняет знак с плюса
на минус,	то есть f x 0	на интервале x0 , x0	и f x 0 на интервале
x0, x0 .	Тогда в силу теоремы 9.1 функция f x		возрастает на интервале
x0 , x0	и убывает на интервале x0, x0 . Это и означает, что x0 точка мак-

симума функции.

Пример 9.1. Исследовать на монотонность и экстремум функцию y 3 3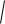 x2 2x; построить ее график.

45

Решение.

Найдем производную y

2

1

2

2.

Производная

не суще-

3

3

x

2

3

3

x

ствует при x 0

и равна нулю при

x 1. Эти точки и есть критические точки

функции. Они разбивают область определения функции − интервал ,

на

три интервала

;0 , 0;1 ,

1; . Исследуем знаки производной на этих ин-

тервалах, результаты оформим в виде таблицы.

y

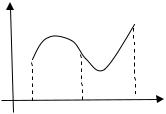
x

;0

0

0;1

1

1;

y

+

0

o

x

y

0

1

1

min

max

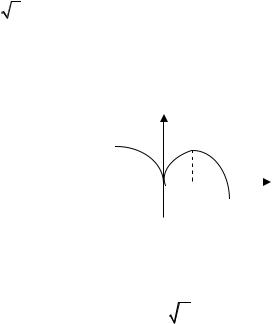
Так как

y

при

x 0,

то в этой точке касательная пер-

Рис.25

пендикулярна оси ox

и экстремум – острый. Так как

y 0

при x 1, то в этой

точке касательная параллельна оси ox и экстремум – гладкий.

При построении графика функции (рис.25) учтем еще,

что

y x 3/ 3

2

и,

x

значит,

y при x ;

y при x .

Теорема 9.4 (второе достаточное условие экстремума).

Пусть

f x0 0 и существует

f x в точке x0 .

Если f x0 0,

то

x0 точка максимума для

f x .

Если f x0 0,

то

x0 точка минимума для f x .

Доказательство. По формуле Тейлора второго порядка

f x f x

f x0

x x

f x0

x x

2

R

x .

0

1!

0

2!

0

2

Учитывая условия теоремы, получим:

f x0

f x

f x f x

x x

2 R

x .

0

0

2!

0

2

x x 2

Так как R

x

бесконечно малая приx x , а

0, то знак f x

совпада-

2

f x0 , а именно:

0

0

0

ет со знаком

если

f x0 0, то f x0 0, значит,

x0 точка максимума,

если

f x0 0,

то f x0 0,

значит, x0 точка минимума.

Пример 9.2. Исследовать на экстремум функцию y sinx cosx для x 0; 2 .

Решение. Найдем производную: y cosx sinx.

Она всюду существует и равна

нулю, если cosx sin x. Поэтому на отрезке 0; 2 получим две критические

точки

x

,

x

5

. Исследовать эти точки на экстремум проще не по знаку

1

4

2

4

первой

производной

в

окрестности точек,

а

по

знаку второй производной

46

a,b

y sin x cos x в самих точках. Так как							0,	5			0, то точка x1
				y				y
													4
				4					4
есть точка максимума, а точка x		5	есть точка минимума данной функции.
2	4

Замечания.

1.Рассмотренные достаточные признаки экстремума не всегда применимы. Иногда удобно исследовать функцию на экстремум, используя определение.

2.Иногда, для упрощения вычислений, удобно перейти от функции f x 0 к

функции c f x , или к функции

f x , или к функции f 2 x . Все эти функции

имеют экстремумы в одних и тех же точках.

9.3. Наибольшее и наименьшее значение функции на отрезке

На практике часто встречаются задачи, в которых требуется найти наибольшее или наименьшее значение функции на отрезке. Напомним, что функция, непрерывная на отрезке, принимает на этом отрезке наибольшее и наименьшее значения. Эти значения она принимает либо в критических точках внутри отрезка, либо на концах отрезка. Поэтому для отыскания наибольшего и наименьшего значения непрерывной на отрезке функции f x следует:

1)найти критические точки функции на интервале a,b ,

2)вычислить значения функции в этих критических точках (не исследуя их) и на концах отрезка,

3)из всех полученных значений функции выбрать наибольшее и наименьшее.

Пример	9.3.	Найти	наибольшее		M и наименьшее		m	значения функции
f x x3 3x2		3x 2 на отрезке 1,			2 .
Решение. Найдем критические точки функции:						f x 3x2 6x 3 3(x 1)2 ;
f x 0	в точке x 1, принадлежащей отрезку 1, 2 .
Вычислим значения			функции	в	критической	точке	и	на концах отрезка:
f 1 1,	f 1 9,		f 2 0.	Поэтому наибольшее значение функции на от-
резке M 0, наименьшее значение					m 9.

9.4. Выпуклость и вогнутость. Точки перегиба

Пусть кривая y f x , x a,b имеет в каждой точке невертикальную ка-

сательную.

Кривая называется выпуклой (соответственно вогнутой), если она расположена ниже (соответственно выше) любой своей касательной.

Точка,отделяющаявыпуклуючастькривой отвогнутой,называетсяточкойперегиба.

47

На рис. 26 дуга			AC кривой y f x ,	x a,c выпуклая, дуга CB кривой
y f x ,	x c,b вогнутая, точка C точка перегиба.
Теорема 9.5 (условие выпуклости).
Если		f x 0	на a,b , то кривая y f x ,		x a,b	выпукла.
Если		f x 0	на a,b , то кривая y f x ,		x a,b	вогнута.

Доказательство. Рассмотрим произвольную точку x0 a,b . Вычислим ордина-

ту точки кривой yкр. , используя формулу Тейлора перво-

y

B

го порядка с остаточным членом в форме Лагранжа:

C

y f x

yкр. f x f x0

f x0

x x0

f c

x x0 2 ,

A

1!

2!

где точка c находится между x и x0 .

a

c

b x

Из уравнения касательной

Рис.26

yкас.

f x0 f x0 x

x0 ,

y

кр.

y

кас.

f c

x x

2 .

0

2!

Если f x 0

a,b ,

на

то

yкр. yкас. 0,

yкр. yкас. .

Следовательно,

кривая

y f x является выпуклой. Аналогично доказывается,

что при

f x 0 кривая

является вогнутой.

Теорема 9.6 (необходимое условие точки перегиба).

y f x . Тогда

Пусть точка с абсциссой

x0

является точкой перегиба кривой

вторая производная

f x

в точке x0

равна нулю или не существует.

Доказательство. Точка перегиба x0,

f x0

отделяет выпуклую часть кривой от

вогнутой. Пусть при x x0

кривая y f x

выпукла, а при x x0

кривая y f x

вогнута. Тогда

при x x0

имеем:

f x 0 и, значит,

f x

убывает;

при x x0

имеем:

f x 0 и, значит,

f x

возрастает.

Это означает, что функция

f x имеет минимум в точке

x0 , следовательно, ее

x

в этой точке или равна нулю, или не существует.

производная f x f

Замечание. Необходимое условие точки перегиба не является достаточ-

ным. Например, кривая

y x4

является вогнутой, так как

y 12x2

0 и,

значит,

не имеет точек перегиба, хотя y 0

при x 0.

Теорема 9.7 (достаточное условие точки перегиба).

Если вторая производная f x

при переходе через точку x0

меняет знак,

то точка x0 ,

f x0 есть точка перегиба кривой y f x .

48

Доказательство. Пусть f	x 0 при x x0 и	f x 0 при x x0 . Тогда кривая
y f x выпукла при x x0	и вогнута при x x0 . Следовательно, точка с абсцис-
сой x0 является точкой перегиба этой кривой.

Итак, для исследования кривой y f x на выпуклость и отыскания точек перегиба нужно:

1)найти точки, в которых вторая производная f x равна нулю или не су-

ществует;

2)рассмотреть интервалы, на которые эти точки разделят область определения функции;

3)исследовать знак f x на этих интервалах.

Пример 9.5. Найти точки экстремума функции f x 3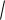x2 1. Исследовать гра-

фик этой функции на выпуклость, найти точки перегиба. Построить график функции.

	Решение. 1). Вычислим первую производную: f x		2x		. Она равна ну-
			(x2 1)2
	3 3

лю при x 0 и не существует (обращается в бесконечность) при x 1. Знаменатель у производной f x положителен, а числитель меняет знак только при

x 0, причем с – на +. Значит,

x 0

точка минимума;

f 0 1.

2). Для исследования на выпуклость найдем вторую производную:

2

1

3 x

2

1

2

x

2x

2 x2 3

3

3

f x

2

x2 1

.

3

x2

1

4

x2 1

5

3

93

Производная

f x

всюду отлична от нуля, но не существует при

x 1,

x 1.

Эти точки разбивают область определения функции

на ин-

y

тервалы ; 1 ,

1,

1 ,

1; . Исследуем знаки второй

производной на этих интервалах, результаты оформим в виде

таблицы.

1 0

1 x

x

, 1

1,1

1,

1

f x

−

+

−

y f x

выпукла

вогнута

выпукла

Рис 27

Точки с абсциссами x 1 являются точками перегиба. Их ординаты y 0.

3). Для построения графика функции (рис.27) сначала нанесем точку минимума0; 1 , затем точки перегиба 1;0 , 1;0 и учтем данные таблицы.

49

9.5. Асимптоты графика функции

Асимптотой кривой называется прямая, расстояние до которой от точки , лежащей на кривой, стремится к нулю при неограниченном удалении этой точки по кривой от начала координат.

Пример 9.6.	Кривая y 1/ x (рис.28) имеет вертикальную		y	1
			y
асимптоту x 0	и горизонтальную асимптоту y 0.
				xx
			o
Отыскание вертикальных асимптот			Рис 28
Для отыскания вертикальных асимптот кривой y f x		следует исследо-

вать точки разрыва функции f x и граничные точки ее области определения.

Если lim f x , то прямая x x0

есть вертикальная асимптота.

x x0

f x , то прямая

Если только правосторонний предел

lim

x x0 явля-

x x0 0

ется правосторонней вертикальной асимптотой.

Пример 9.7. Имеют ли вертикальные асимптоты следующие кривые

а) y

ex

, б) y e 1/ x ,

в)

y ln x,

г)

y

sin x

?

x 3

x

Решение. а). Функция y

ex

имеет точку разрыва

x 3. Так как lim

ex

, то

x 3

x 3

x 3

прямая x 3 является вертикальной асимптотой.

б). Функция y e 1/ x имеет точку разрыва x 0. Так как

lim e 1/ x

,

lim e 1/ x 0,

x 0

x 0

то прямая x 0 является только левосторонней асимптотой.

в). Функция y ln x определена на интервале 0,

и не имеет точек разрыва.

Исследуем граничную точку x 0 области определения. Так как

lim

ln x , то

x 0

прямая x 0 является правосторонней асимптотой.

sin x

г). Функция y

sin x

имеет точку разрыва x 0, но lim

1. Поэтому прямая

x

x 0

x

x 0 не является асимптотой.

Отыскание невертикальных асимптот

Теорема 9.8. Кривая y f x

имеет невертикальную асимптоту

y k x b тогда

и только тогда, когда существуют конечные пределы

k lim

f x

,

b

lim

f

x

kx .

x

x

x

50