MatAn_thory

Отметим, что при вычислении определенного интеграла по формуле (15.7) не надо возвращаться к старой переменной, как это приходилось делать при замене переменной в неопределенном интеграле. Рекомендации по выбору новой переменной такие же, как и для неопределенного интеграла.

9
			x
Пример 15.6. Вычислить интеграл
					d x .
			1
		x
4

Решение. Введем новую переменную t, положив

x

t .

Тогда x t2, dx 2td t .

Найдем пределы изменения новой переменной

t

: при

x 4 имеем

t 2;

x

при x 9

имеем t 3. Поэтому, в соответствие с формулой (15.7)

9

3 t 2tdt

3

(t2 1) 1

3

1

dt

2

3

x

dx

2

dt 2

t 1

2

t

t ln t 1

7 2ln2.

t 1

t 1

t 1

x

1

4

2

2

2

2

2

1

Пример 15.7. Вычислить интеграл

4 x2 dx.

0

Решение. Чтобы исчез корень под знаком интеграла,

положим x 2sint .

Тогда

4 x2

4 4sin2 t

2cost . Найдем dx 2costdt

и пределы изменения новой пе-

ременной: при x 0

имеем sint 0,

t 0;

при x 1 имеем sint

1 ,

t /6 .

2

1

6

6

sin2t

3

2

6

Тогда

4 x

dx 2cost 2costdt 2 1 cos2t dt 2 t

2

0

3

.

2

0

0

0

С помощью замены переменной выведем ряд полезных следствий.

Следствие 1. Если функция

f x − нечетная на отрезке a,a , то

a

f(x)dx 0.

a

a

0

a

Действительно, имеем: I

f (x)dx

f(x)dx f (x)dx I1 I2 .

a

a

0

В интеграле I1 сделаем замену переменной x t. Тогда dx dt ; в силу

нечетности функции, f x f t f

t . При x a имеем t a ;

при x 0 име-

ем t 0. Поэтому

a

0

0

I1 f (x)dx f (t)dt f (t)dt I2 ,

I I1 I2 0.

a

a

0

Следствие 2. Если функция

f x − четная на a,a , то

a

a

f(x)dx 2 f(x)dx .

a

0

Эта формула выводится так же, как предыдущая.

Пример 15.8. Вычислить интеграл I

/4

x7 3x5

2x3 x 4

dx.

cos

2

x

/4

81

Решение. Функция x7 3x5 2x3 x является нечетной, так как числитель есть cos2 x

функция нечетная, а знаменатель – функция четная. Поэтому интеграл от этой

функции по симметричному промежутку						равен нулю. Функция				4	является
										cos 2x
	/4		4dx	/4	4dx	8tg x|0		/4
четной, поэтому I				2					8.
			2		2
	/4		cos x	0	cos x
	Следствие 3. Пусть функция f x						имеет период T. Тогда
		a T		T			для любого числа a.
			f(x)dx f(x)dx
			a	0

Для вывода этой формулы воспользуемся свойством 4 определенного интеграла

		a T		0	T	a T
			f(x)dx f(x)dx f(x)dx f(x)dx .
		a		a	0	T
В последнем интеграле сделаем замену x y T . Тогда dx dy, а							в силу перио-
дичности функции f x f y T f y . При x T						имеем y 0;	при x a T
a T			a		a	0
имеем y a. Поэтому		f(x)dx f(y)dy			f(x)dx f(x)dx,
	T		0		0	a
a T			0	T	0	T
	f(x)dx f(x)dx f(x)dx f(x)dx f(x)dx.
a			a	0	a	0
Пример 15.9. Вычислить		2 sin5 xdx.
Решение. Функция sin5 x		0
		имеет период 2 , равный длине промежутка интегри-

рования. Используя следствие 3, сдвинем промежуток интегрирования вдоль оси

OX на	и, так как функция sin5 x − нечетная, воспользуемся следствием 1.
	2
Поэтому		sin5 xdx sin5 xdx 0 .

16.Геометрические приложения определенного интеграла

16.1. Площадь плоской фигуры

Пусть

фигура

в

плоскости

XOY

ограничена

линиями

y y x , y 0,

x a, x b, причем

y x − непрерывная неотрицательная функция

на a,b (рис.37).

y

y y x

0

x

1

x

k

xn

x

x

x

k

x

1

n

Рис.37

82

Разобьем отрезок a,b на n частичных отрезков с длинами x1, x2 ,..., xn . Через точки деления проведем вертикальные прямые, которые разделят фигуру на n вертикальных полосок. Каждую k -ю вертикальную полоску заменим прямоугольником площади Sk с основанием, равным xk , и высотой, равной y(xk), где xk − произвольно выбранная точка на k -м частичном отрезке. Тогда

Sk y(	x	k) xk	k 1,2,...,n .
				n	n
Суммируя площади всех прямоугольников, получим				Sk y(		x	k) xk.
Площадь S заданной фигуры определяется как				k 1	k 1
				предел	полученной суммы

n

S lim y(

x

k) xk. при стремлении к нулю d max xk . Мы получили предел

d 0k 1

1 k n

интегральной суммы непрерывной функции y x

по отрезку a,b , то есть инте-

b

грал y(x)dx . Таким

образом,

площадь

фигуры,

ограниченной

линиями

a

y y x , y 0, x a, x b, при условии,

что y x 0, вычисляется по формуле

b

b

S y(x)dx или S ydx .

(16.1)

a

a

y

a

Пример 16.1. Вычислить интеграл

a2 x2

dx.

0

Решение. Интеграл такого типа был вычислен заменой пере-

a

0

a

менной x a sint

в примере 15.7. Рассмотрим другой спо-

a

Рис. 38

соб. Исходя из формулы (16.1),

интеграл

a2 x2 dx

чис-

0

ленно равен площади фигуры, ограниченной линиями

y

a2 x2

,

y 0,

x 0,

x a . Построим эти линии, учитывая,

что уравнение y

a2

x2

определяет ту

часть окружности

x2 y2 a2

, где y 0 (рис.

38). Полученная фигура есть чет-

верть круга с площадью S 4a2

. Таким образом,

y

y y2 x

a

a2

a

2

x

2

dx

4 .

0

Перейдем к более общему случаю. Пусть фигура в

плоскости

XOY

ограничена

линиями

y y1(x), y y2(x),

x a,

x b,

причем

y2(x) y1(x)

на

a,b

a

y y1 x b

(рис.39). Аналогичным образом, как и в предыдущем случае,

Рис.39

можно получить следующуюформулу для площади

S такой фигуры:

b

S [y2(x) y1(x)]dx.

(16.2)

a

83

x

x

Иногда вычисления значительно упрощаются, если поменять ролями оси

OX и OY . Пусть фигура в плоскости XOY ограничена линиями x x1 y ,

x x2 y ,	y c,	y d , причем x2(y) x1(y)			на отрезке c,d		(рис.40). Тогда
			d	[x (y) x (y)]dy.			(16.3)
			S
			c	2	1

	Пример 16.2. Вычислить площадь фигуры, ограниченной ли-					y
						d
	ниями y ex, y e x, x 1.
	Решение. Построим заданные линии и заштрихуем фигуру,
	ограниченную этими линиями (рис. 41). Снизу фигура огра-							x
	ничена линией	y ex y1(x), сверху – линией y e x y2(x),	x x1 y
	x 1, 0 . Для вычисления площади фигуры воспользуемся					c		x x2 y
							Рис.40
	формулой (16.2):
							y
	0	0
	S [y2(x) y1(x)]dx (e x ex) dx ( e x ex)|01 e e 1 2.				y e x			y ex
	1	1
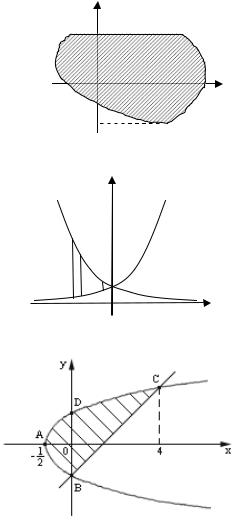
	Пример 16.3. Вычислить площадь фигуры, ограниченной линия-
	ми y2 2x 1, y x 1.
	Решение. Уравнение y2 2x 1 или y2 2 x 1/ 2 определяет							x
	параболу с вершиной A 1/ 2, 0 , осью симметрии − осью OX		1		0
							Рис.41

(рис. 42). Уравнение y x 1 определяет прямую, проходящую через точки 0, 1 , 1,0 . Найдем точки пересече-

ния параболы и прямой, решив систему уравнений: y2 2x 1, y x 1. Получим точку B 0, 1 иточку C 4,3 .

Вычислим площадь фигуры по формуле (16.3). Для

этого нужно записать уравнения кривых, ограничиваю-

Рис.42

щих фигуру, в виде, разрешенном относительно x. Слева

фигура

ограничена

дугой параболы CAB, на которой

x

y2 1

, справа –

отрезком прямой BC, на котором

x y 1; y меняется от

2

yB 1 до yC 3 . Поэтому по формуле (16.3) имеем

3

y2 1

(y 1)2

3

1

y3

3

16

S (y 1)

dy

1

y

5,33.

1

2

2

2

3

1

3

16.2. Объем тела вращения

Рассмотрим тело,

образованное вращением вокруг оси

OX фигуры, ограни-

ченной непрерывной кривой

y y x , осью OX и прямыми x a, x b

(рис. 43).

Разобьем отрезок a,b

на n частей точками

a x0

x1 x2

... xn b.

Проведем

через точки деления плоскости,

перпендикулярные оси OX . Сечение тела вра-

84

y(xk)

y2 (xk)

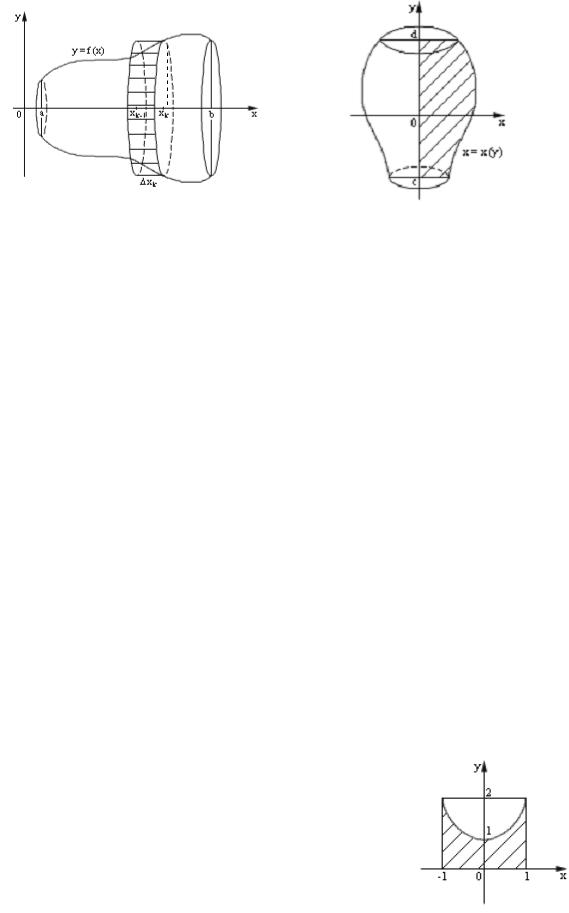
щения плоскостью x xk есть круг радиусом с площадью

k 1,2,...n . Проведенные плоскости разобьют тело на слои. Каждый k -й слой

y xk

Рис.43 Рис.44

приближенно заменим прямым цилиндром (рис.43) с радиусом y(xk), высотой

x	x x	k 1	и объемом	V	S h y2(x ) x				k	k 1,2,...n .
k	k			k			k
						n			n
Сумма объемов всех цилиндров равна							Vk	y2(xk) xk .
						k 1			k 1
Объем тела вращения Vox				определяется как предел этой суммы
						n
					VOX lim	y2		(xk) xk.
					d 0 k 1

при стремлении к нулю величины d max{ xk} . Мы получили предел инте-

1 k n

гральной суммы непрерывной функции y2(x) по отрезку a,b , который суще-

b

ствует и равен интегралу y2(x)dx.

a

Итак, объем VOX тела, полученного при вращении вокруг оси OX фигуры, ограниченной кривой y y x , осью OX ипрямыми x a, x b, вычисляется по формуле

		b			b
	VOX y2(x)dx ,			или	VOX y2dx			.		(16.4)
		a			a
Аналогично вычисляется объем VOY			тела, полученного при вращении вокруг оси
OY фигуры,ограниченнойлинией x x(y),осью OY ,прямыми y c,									y d	(рис.44):
		d			d
		VOY x2(y)dy ,		или	VOY x2dy .					(16.5)
		c			c
Пример 16.4. Вычислить объем тела, образованного вращением
фигуры, ограниченной линиями y x2			1, x 1, x 1,			y 0,
а) вокруг оси OX , б) вокруг оси OY .
Решение. Построим параболу y x2 1,				прямые x 1,		x 1, y 0 и

заштрихуем фигуру, ограниченную этими линями (рис.45).

85

f x

a,b

V1 R2H 2

Рис.45

Объем тела, полученного при вращении этой фигуры вокруг оси OX , вычислим по формуле (16.4):

1 1

VOX y2 dx (x2 1)2 dx.

1 1

Так как подынтегральная функция − четная, то удобно воспользоваться след-

ствием 2 (п. 15.3)

	1		1		56
V 2		(x2 1)2dx 2		(x4 2x2 1)dx		.
OX					15
	0		0

Для вычисления объема тела вращения фигуры вокруг оси OY нельзя непосредственно воспользоваться формулой (16.5), так как фигура сверху ограничена не прямой, а параболой. Поэтому сначала рассмотрим фигуру, ограниченную прямой x 1, осью OY , прямыми y 0, y 2. При ее вращении вокруг оси OY получим цилиндр, объем которого V1 можно вычислить по формуле

или по формуле (16.5)

		2		2
		V1 x2 dy dy 2 .
		0		0
	Теперь рассмотрим фигуру, ограниченную линиями						y x2 1, осью OY и пря-
	мой y 2. При ее вращении вокруг оси OY		получим тело, объем которого V2
	вычислим по формуле (16.5)
	2	2			y2	y)|2		.
	V2 x2dy (y 1)dy (
	1	1		2			1	2
	Тогда искомый объем VOY будет равен разности V1 V2 :
	V V V 2			3 .
	OY	1 2	2	2

17. Несобственные интегралы

При введении определенного интеграла мы предполагали, что отрезок

– конечный, а функция ограничена на этом отрезке. Если нарушается хотя

бы одно из этих условий, то вводят обобщение определенного интеграла – несобственные интегралы.

17.1. Несобственный интеграл первого рода (по бесконечному промежутку)

Несобственный интеграл первого рода (по бесконечному промежутку) определяется следующим образом:

	b	b		.	(17.1)
			f(x)dx
	f(x)dx lim
a		a

Если этот предел существует и конечен, то говорят, что несобственный интеграл сходится. Если же этот предел не существует или бесконечен, то говорят, что несобственный интеграл расходится.

86

Аналогично определяется несобственный интеграл и для промежутка ,b :

b		b		.	(17.2)
	f(x)dx	a	f(x)dx
		lim
		a

Для промежутка , , несобственный интеграл определяется равенством

		c
	f (x)dx		f (x)dx f (x)dx	,	(4.3)
			c

где c любое число. Несобственный интеграл в левой части называется сходящимся, если сходится каждый несобственный интеграл в правой части.

Обобщенная формула Ньютона-Лейбница

Пусть F x – первообразная для функции f x на промежутке a, . Вос-

пользуемся формулой Ньютона-Лейбница для интеграла b f(x)dx. Тогда

a

a

Если обозначить

f(x)dx		lim	b	f(x)dx lim [F(b) F(a)]			lim F(b) F(a) .
	b		a	b			b
F =		lim	F(b) , то можно записать
		b
		f(x)dx F( ) F(a) F(x)				.	(17.4)
					a
		a

Аналогично, если обозначить F = lim					F(b) , то
			b
	b		b
		f(x)dx F(x)		,		f(x)dx F(x)		.	(17.5)

Пример 17.1. Вычислить несобственные интегралы или доказать, что они расхо-

							dx2 ,									dx			0		dx
дятся: 1)												2)					,	3) cosxdx, 4)	ex dx, 5)				.
																						2
Решение.			1				x								1	x		0			1 x
			Воспользуемся обобщенной формулой Ньютона-Лейбница:
1)		dx2 1					(0 1) 1,										интеграл сходится;
	1	x	x				1
2)		dxx ln													интеграл расходится;
						x						,
											1
	1
3)		cosxdx sin x | 0															sin x ; этот предел не существует,
															lim
	0														x
		поэтому интеграл расходится;
	0
4)		ex dx ex								0		e0					ex 1 0 1, интеграл сходится;
															lim
															x
5)		dx																) , интеграл сходится.
			arctgx
																(
		2
		1 x													2			2
																		87

Геометрический смысл несобственного интеграла

		b
Пусть	f(x) 0	на промежутке a, . Тогда f(x)dx	численно равен площади
		a
фигуры,	ограниченной снизу отрезком a,b оси OX ,		сверху – линией y f x ,

слева и справа –	прямыми x a и x b (рис.46). При	y
возрастании b прямая x b , ограничивающая эту фигу-
	b
ру, движется вправо, а интеграл f(x)dx стремится к ин-
	a
		0	a
тегралу f(x)dx.	Поэтому величину интеграла f(x)dx
a	a

естественно принять за площадь бесконечной фигуры, ограниченной снизу осью OX , сверху − графиком функции y f x , слева – прямой x a (рис.46).

b	f x 0 численно равен
Аналогично, f(x)dx для случая

площади бесконечной фигуры, ограниченной снизу осью OX, сверху − кривой y f x , справа − прямой x b (рис.47).

y f x

b

Рис.46

y

y f x

Рис. 47 0

Пример 17.2. Вычислить площади фигур, ограниченных осью OX , прямой x a ,

	линией y f x , если	а) f x	1	, a 1,	x 1;	б) f x	1 , a 1,			x 1;
			x2
							x
		в) f x ex , a 0,			x 0;	г) f x		1	,	x ( , ) .
							1 x2

Решение. Построим фигуры, ограниченные данными линиями (рис.48, 49, 50, 51). Воспользуемся результатами примера 17.1:

	dx2 1;		dx		0		dx
а) S		б) S		;	в) S exdx 1;	г)			.
							1 x	2
1	x	1	x

Итак, фигуры, изображенные на рис.48, 50, 51 имеют конечные площади, а фигура, изображенная на рис. 49, имеет бесконечную площадь.

x

b x

Рис.48	Рис.49	Рис.50	Рис.51
	4.2. Несобственный интеграл второго рода

88

17.2. Несобственный интеграл второго рода

(от неограниченной функции)

Пусть функция f x неограничена вблизи точки x b

(рис.52). Несобственный интеграл второго рода (от неограниченной функции) определяется следующим образом:

b

b1

	f (x)dx	b b 0			f (x)dx.	(17.6)
			lim
a		1		a

Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, в противном случае несобственный интеграл называется расходящимся.

Аналогично для функции f x , неограниченной вблизи

					b
точки x a (рис. 53), несобственный интеграл					f(x)dx опре-
деляется следующим образом:					a
	b			b
		f(x)dx	lim		f(x)dx.
			a a 0
	a		1	a1

y

y f x

0 a Рис. 52 b1 b x

y

y f x

a a1 0

b x

Рис.53

(17.7)

Для функция f x	неограниченной вблизи точки x c	a c b (рис. 54)
	b

несобственный интеграл f(x)dx определяется равенством

a

b c b

f(x)dx f(x)dx f(x)dx .
a	a	c

Если каждый из интегралов в правой части равенства схо-

b

дится, то несобственный интеграл f(x)dx называется схо-

a

дящимся, в противном случае – расходящимся.

y

y f x

0 a

c

b x

Рис.54

Для функции f x , неограниченной вблизи точки x b, имеем аналог фор-

мулы Ньютона-Лейбница для несобственного интеграла второго рода:

	b		b		,	где F b =		F(x).			(17.8)
	f(x)dx F(x)						lim
	a		a			x b 0
Аналогично для функции		f x , неограниченной вблизи точки x a,
	b			b	,	где F a =		F(x).
		f (x)dx F(x)					lim
	a			a			x a 0
					89

Пример 17.3. Вычислить несобственные интегралы или доказать, что они расхо-

2

dx

1

dx2 .

дятся:

а)

,

б)

2 x

0

1

x

1

Решение. В первом интеграле подынтегральная функция

f x

неогра-

2 x

ничена при x 2, поэтому интеграл

2

dx

является несобственным. Применим

2 x

0

обобщенную формулу Ньютона-Лейбница:

2

dx

2 d (2 x)

2

2

2 x

0 (0 2 2) 2 2 .

2 x

2 x

0

0

f x

1

Во втором интеграле подынтегральная функция

неограничена вблизи

x2

1

dx2

0

dx2

1

точки

x 0.

Поэтому,

по определению,

dx2 ,

при

этом

1

x

1

x

0

x

0

0 . Поэтому интеграл

1

− расходится. Отметим, что если бы мы

dx2

1

dx2

1 x

x

1

1 x

стали вычислять данный интеграл, не обращая внимание на разрыв подынте-

гральной				функции в			точке	x 0,	то получили бы	неверный результат
1			1 (1 1) 2.
dx2		1
1 x		x	1
Геометрический смысл несобственного интеграла второго рода для функ-
ции	f x			неограниченной				вблизи	точки x b : если	f x 0 (рис. 52), то
	b1				b		естественно принять за площадь бесконечной фигуры,
lim		f(x)dx				f(x)dx
b b 0
1	a				a

ограниченной снизу отрезком a,b оси OX , сверху – линией y f x , слева и справа – прямыми x a, x b.

17.3.Гамма-функция

Втеории вероятности, математической физике и ряде других разделов используется несобственный интеграл, называемый гамма-функцией:

Г p x p 1e xdx .

0

Отметим ряд свойств гамма-функции.

1). Гамма-функция определена при p 0, т.е. интеграл		Г p x p 1 e xdx схо-
		0
дится при p 0 и расходится при	p 0 (это свойство примем без вывода).
	90