MatAn_practice

x 1 2x 1

Пример 1.13. Вычислить lim

.

x x 2

. Выделим целую часть дроби

Решение. Имеем неопределенность вида 1

x 1

x 2 3

3

3

3

x 2

1

.

Так как

0 при

x , то

3

e и

lim 1

x 2

x 2

x 2

x 2

x

x 2

x 2

3

2x 1

x 1

2x 1

3

2x 1

3

x 2

lim

6x 3

3

6

x

lim

1

lim 1

lim

1

e

x 2 e

.

x

2

x 2

x x 2

x

x

1

1 3x

Пример 1.14. Вычислить lim

sin2x

.

1 x

x 0

Решение. Имеем неопределенность вида 1 . В отличие от предыдущего при-

мера, удобнее свести выражение ко второму замечательному пределу отдельно в числителе и в знаменателе:

1

1/3x

3x

1

3x

3

lim(1 3x)sin2x

1

lim

1 3x

sin2x exp lim

exp

e3/2;

2

x 0

x 0

x 0 sin2x

1

1

1/ x ( x)

x

1

1/2

sin2x

sin2x

lim(1 x)

1 ( x)

e

.

1

lim

exp lim

exp

2

x 0

x 0

x 0 sin2x

			1				1
		1 3x					(1 3x)		sin2x
Поэтому	lim				sin2x	lim
								1
	x 0		1 x			x 0
							(1 x)sin2x

x

3/2

e 1/2 e2.

e

Пример 1.15. Вычислить

lim(3 2x)1 x .

x 1

Решение. Имеем неопределенность вида

. Для того чтобы воспользоваться

1

вторым замечательным пределом, выделим в скобке единицу:

3 2x 1 (2 2x) 1 2(1 x).

Произведем замену переменной: t 1 x,

где t 0

при x 1. Тогда

x

1 t

2t (1 t)

1/2t

e2 .

t

lim(3 2x)1 x lim(1 2t) t

lim

1 2t

exp lim

2(1 t)

x 1

t 0

t 0

t 0

2x 1 x

Пример 1.16. Вычислить

lim

.

2x 1 x

x

x 1

2

,при x .

Решение. lim

x

x 1

0,при x

Пример 1.17. Вычислить lim (x 5) ln(x 3) ln x .

x

Решение. Воспользовавшись свойствами логарифмов, получим

11

lim (x 5)(ln(x 3) ln x) ( )

x
		3			x 5				3		x/3
ln lim		1				ln lim		1
			x						x
x						x

		x 3 x 5				x 3 x 5
	lim	ln			ln lim
			x				x
	x				x
	x 5 3/x			lim	3x 15 / x
			ln e x		lne 3 3.

2. Непрерывность функции

Функция f x непрерывна в точке x0 , если	lim f (x) f (x0).
	x x0

Это равенство означает выполнение трех условий:

1)функция f x определена в точке x0 и ее окрестности,

2)функция f x имеет предел при x x0 или, что равносильно, существу-

ют и равны односторонние пределы f (x0 0) и f (x0 0),

3) предел функции f x при x x0 равен значению функции в точке x0 .

	Пример 2.1. Исследовать на непрерывность функцию f (x)			x 3		.
			x2	5x 6 2

Решение. Эта функция элементарна и определена для всех x, кроме нулей знаменателя x 2, x 3. Поэтому она непрерывна во всех точках x, кроме x 2, x 3; точки x 2, x 3 являются точками разрыва функции. Для установления типа точек разрыва преобразуем функцию и найдем пределы

f (x)

x 3

x 3

x 3

,

x2 5x 6

x 2

x 3

x2 5x 6 2

f (x) ,

lim

x 2

lim

f (x) lim

x 3

lim

x 3

lim

1

1,

x 2

x 3

x 2

x 3

x 2

x 3 0

x 3

x 3

x 3

x 3

x 3

x 3

1

lim f (x) lim

lim

lim

1.

x 2

x 3

x 2

x 3 1

x 2

x 3 0

x 3

x 3

x 3

x 3

Так как в точке x 2 предел бесконечен, то x 2 – точка разрыва 2 рода;

в точке x 3 односторонние пределы конечны, но не равны между собой, следовательно, x 3 – точка конечного разрыва 1 рода (скачок).

		x,	x 1,
Пример 2.2. Исследовать на непрерывность функцию		2,	x 1,
	f (x) x2
		0,	x 1.

Решение. При x 1	и x 1 функция	f (x)совпадает с непрерывными элемен-
тарными функциями, следовательно, непрерывна. Исследуем точку x 1:
lim	f (x) lim x 1,	lim	f (x) lim x2 2 1.
x 1 0	x 1	x 1 0	x 1

Односторонние пределы существуют, конечны и равны между собой, то есть

существует lim f x 1, но	f ( 1) 0	lim f (x) и, следовательно, x 1 есть
x 1		x 1

точка устранимого разрыва 1-го рода.

12

Пример 2.3. Исследовать функцию на непрерывность, указать тип точек

1

tg x

2

1/ x

1

1

, x 0,

разрыва: а)

f (x)

, б)

f (x)

,

в) f (x)

,

г) f (x) sin x

ln

x

x

2

1/ x

1

0,

x 0.

Решение. а). Функция

f (x)

1

не определена в точках

x 0,

x 1,

x 1. В

ln

x

точках x 0,

x 1,

x 1 функция

f (x)

является суперпозицией элементарных

функций, непрерывных на своей области определения; поэтому функция f (x)

непрерывна во всех точках, кроме точек					x 0, x 1,	x 1.			Исследуем функ-
цию в точке x 0. Так как lim ln		x		, то lim f (x) lim			1		0. Предел функ-
x 0					x 0	x 0 ln		x
ции при x 0 существует, но функция f					(x) в точке x 0 не определена, поэто-

му x 0 точка устранимого разрыва 1-го рода. Разрыв можно устранить, если

f (x) доопределить,

положив f (0) 0,

тогда функция

f (x)

будет являться не-

прерывной в точке x 0.

x 1.

Исследуем

функцию

в

точках

Так

как

lim ln

x

0, то

1

x 1

lim f (x) lim

.

Пределы

функции

при

x 1

бесконечны,

следова-

x

x 1

x 1 ln

тельно, x 1 − точки разрыва второго рода.

б). Функция

f (x)

tg x

не определена в точках x 0 и x

n

n

(n Z). В дру-

x

2

гих точках функция

f (x)

является непрерывной как частное двух непрерывных

элементарных функций.

Исследуем точку

x 0:

по следствию из первого замечательного предела

lim

tgx

1,

но

f (0)не существует. Поэтому x 0 − точка устранимого разрыва.

x 0 x

tg x

Исследуем точки x

n

(n Z).

Так как

lim tg x , то

lim

.

2

n

x xn

x xn x

Следовательно, x

n

(n Z)

− точки разрыва 2-го рода.

2

n

в). Функция f (x)

21/ x 1

при всех x 0

непрерывна как частное двух непрерыв-

21/ x 1

ных функций. В точке x 0 функция

f (x)

не определена, следовательно, x 0 −

точка разрыва. Исследуем эту точку. Предварительно заметим, что

lim

1

,

lim

21/ x 0;

x 0 0 x

x 0 0

lim

1

,

lim 21/ x ,

x 0 0 x

x 0 0

следовательно, lim

f (x) lim

21/ x 1

0 1

1,

x 0 0

x 0 0 21/ x 1

0 1

lim

f (x)

lim

21/x 1 2 1/x

lim

1 2 1/x

1 0

1.

1/x

1 2

1/x

x 0 0

x 0 0

2

x 0 0 1 2

1/x

1 0

13

Таким образом, при x 0 односторонние пределы конечны, но различны, поэтому в точке x 0 − конечный разрыв 1-го рода (скачок).

	1
г). Функция			, x 0,	при x 0 непрерывна как элементарная функция.
	f (x) sin x
	0,		x 0.
Точка x 0 − точка разрыва 2-го рода, так как lim					f (x) limsin	1	не существует.
				x 0	x 0 x

3.Производные

3.1.Определение производной и дифференциала

	f x lim	f x	lim	f x x f x	.	(3.1)
		x		x
	x 0		x 0

Функция f x дифференцируема в точке x тогда и только тогда,

когда существует ее производная в этой точке.

Выражение d f x f x dx есть дифференциал функции.

Из дифференцируемости функции следует ее непрерывность. Обратное неверно.

Пример 3.1. Является ли функция f x дифференцируемой? непрерывной?

		1
а)					x 0,
	f x x sin x,
		0,			x 0.

б)	x 1,			x 0,
	f x	x	,	x 0.
	e

Решение. Имеет смысл сначала исследовать функцию на дифференцируемость, так как из дифференцируемости следует её на непрерывность.

а). В точках x 0 функция f (x) дифференцируема как суперпозиция дифференцируемых функций и, следовательно, непрерывна.

Исследуем точку x 0. Найдем предел

f (0)

f (0 x) f (0)

x sin

1

0

1

lim

lim

lim

x

lim sin

.

x

x

x 0

x 0

x

x 0

x 0

x

Этот предел не существует, следовательно,

функция

f (x) не является диффе-

ренцируемой в точке x 0. Но функция

f (x)

непрерывна в точке x 0, так как

lim f x lim x sin

1

0 f 0 .

x

x 0

x 0

При этом мы учли, что при x 0 произведение бесконечно малой x на ограни-

ченную функцию sin 1 являетсябесконечно малой и имеет предел, равный нулю.

	x	x 1,				x 0,
б). Исследуем функцию							на дифференцируемость.
		f (x)		x	,	x 0,
В точках x 0	функция	e						(x) 1;
		f (x) x 1 дифференцируема, так как f
В точках x 0	функция	f (x) e	x						x	.
					дифференцируема, так как f (x) e

Из дифференцируемости функции следует ее непрерывность в этих точках.

14

Исследуем точку x 0:			1,		1 . Так как
	f 0 x 1	x 0		f 0 ex
					x 0

f 0 f 0 1 , то f 0 1. Следовательно, функция f (x) в точке x 0 диффе-

ренцируема, а значит и непрерывна.

3.2. Геометрический смысл производной

Значение производной f x0 равно угловому коэффициенту касательной,

проведенной к кривой y f x в точке M0 с абсциссой x0 : f x0 kкас

Уравнение прямой, проходящей через точку M0 x0, y0 , с угловым коэффици-

ентом k имеет вид:

y y0 k x x0

.

Для записи уравнения касательной или нормали нужно положить в этом урав-

	нении y0 f x0 и						kкас f (x0)		или kнорм								1			соответственно.
																f (x0)
	Пример 3.2. Какой угол образует с осью абсцисс касательная к кривой
	y	2	x5		1	x3 , проведенная в точке с абсциссой x 1.
	3			9						10			1
	Решение. Находим производную y										x4			x2 ; при						x 1 имеем y 1 3, то есть
	tg 3, откуда arctg3 71 34 .								3			3
	Пример 3.3. Составить уравнения нормали к линии y x3 3x2 5 , парал-
	лельной прямой 2x 6y 1 0.
	Решение. Для прямой 2x 6y 1 0 имеем:											y				1	x	1		, угловой коэффициент k	1	.
							1					3					6			3
	Для нормали k							. Так как искомая нормаль параллельна данной прямой,
							y x0

то их угловые коэффициенты совпадают. Поэтому:

k		1		1	y x0 3 3x02 6x0 3 3x02 6x0 3 0 3(x0 1)2 0, x0 1.
		y x0
			3
Подставляя k						1	,	x 1,	y	y( 1) ( 1)3 3( 1)2					5 3 в уравнение нормали
			3					0	0			1				1		8
y y0		k x x0 , получим:							y 3				(x 1) или y				x		.
											3				3		3
Пример 3.4. Найти угол между параболами															y 8 x2,					y x2 .
														2
									y 8 x					, найдем точки пересечения парабол:
Решение. Решив систему											2
									y x

A 2;4 , B 2;4 . Продифференцируем обе части каждого из уравнений парабол: y 2x, y 2x. Найдем угловые коэффициенты касательных к параболам в точке A (то есть значения производных при x 2): k1 4, k2 4.

Теперьнайдемугол 1 междупараболами,тоесть междуихкасательнымивточке A:

15

tg		k2 k1			4 4			8	,		arctg				8	.
		1 k k			1 16		15							15
1			2							1
		1

8

Аналогично, найдем угол 2 между касательными в точке B : 2 arctg .

15

3.3. Дифференцирование по формулам

При изучении этой темы следует использовать таблицу производных и правила дифференцирования.

Правила дифференцирования

1. u v u v ,

2.

uv

,

в частности,

c u

,

где с − число,

uv

uv

c u

u

c

3.

,

в частности,

, где с − число,

v2

v2

v

v

4.

yx yu

ux ,

где

y y u ,

u u x ,

5.

1

0).

yx

xy

(xy

Формулы дифференцирования

1

1

1

1.

xa a xa 1 ,

в частности,

,

x

;

x

2

x

x

2

2.

ax ax lna,

в частности,

ex ex ;

1

1

3.

loga x

,

в частности,

lnx

;

x

xlna

4.

sin x

cosx,

sin x

;

cosx

1

1

5.

tg x

cos2 x

,

ctg x

sin2 x

;

1

1

6.

arcsin x

,

arccosx

;

1 x2

1 x2

1

1

7.

arctgx

1 x2

,

arcctgx

1 x2

;

ch x,

8. sh x

ch x sh x ;

1

1

9.

th x

ch2 x

,

cth x

sh2 x

.

Пример 3.5. Применяя формулы и правила дифференцирования, найти производные следующих функций:

а) y x2ex ,	б) y	arcsin x	,	в)	y 5cosx x2 ln x .
		x
Решение. а). Воспользуемся формулой uv				u v	v u , из которой следует, что

16

y x2ex x2 ex ex x2 2xex x2ex .

u				u v vu
б). Воспользуемся формулой							, тогда
					v2
v

x

1

arcsin x

arcsin x (x)

x

1 x

2 arcsin x

arcsin x

x arcsin x

1 x2

y

.

x

x2

x2

x2 1 x2

1

в). y 5cos x x2

ln x

5 (cos x) (x2) (ln x) 5sin x 2x

.

x

Пример 3.6. Найти производную сложной функции:

а) y (2x3 5)4 ,	б) y tg6 x ,	в) y lntg	x	.
		2

Решение. По правилу дифференцирования сложной функции, если y y(u), u u(x), то yx yu ux .

а). Обозначим 2x3 5 u , тогда y u4 . Таким образом, имеем:

y (u4)u (2x3 5)x 4u3 (6x2) 24x2(2x3 5)3 .

6

5

5

1

б). Для функции y tg

x имеем: y

6 tg

x cos2 x .

x (tg x) 6 tg

в). Для функции y lntg

x

имеем:

2

1

x

1

1

x

1

1

1

y

.

tg

x

2

x

2

x

2

x

2

sin x

tg

sin

cos

x

tg

cos

2

2

2

2

2

Пример 3.7. Найти y(n) , если

а)

y ln x ,

б)

y 2x .

Решение. а). Для функции

y ln x

имеем:

y

1

,

y 1 x 2 ,

y 1 ( 2)x 3,

y(4) ( 1)( 2)( 3)x 4 ,…,

x

(n 1)!

y(n) 1 2 3 ... (n 1)( 1)n 1x n ( 1)n 1

.

б). Для функции

y 2x имеем:

xn

y n

y 2x ln2,

y 2x ln2 2,

y

2x ln3 2,...,

2x lnn 2.

3.4.Логарифмическое дифференцирование

Вряде случаев для нахождения производной функции y f x удобно это ра-

венство сначала прологарифмировать, а затем продифференцировать. Такой прием называют логарифмическим дифференцированием. Его полезно применять для дифференцирования произведения многих сомножителей, или для дифференцирования частного, числитель и знаменатель которого содержит несколько множите-

лей, или для дифференцирования степенно-показательных функций u x v x .

Пример 3.8. Найти производную y (sin x)tg x .

17

Решение. Здесь основание и показатель степени зависят от x. Логарифмируя, получим ln y tgx ln(sin x). Продифференцируем обе части последнего равен-

ства по x:

(ln y)x (tg x) ln(sin x) tgx (ln(sin x)),

1

yx

1

lnsin x tg x

1

cosx,

y

cos2

sin x

x

lnsin x

tg x

lnsin x

yx

y

1

(sin x)

1 .

2

x

2

x

cos

cos

Пример 3.9. Найти производную функции y 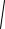x sin x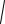1 ex .

Решение. Находить y как производную произведения слишком громоздко. Удобнее применить логарифмическое дифференцирование:

ln y ln

xsin x 1 ex

ln

x

ln

sin x

ln 41 ex ,

ln y 1 ln x 1 lnsin x 1 ln(1 ex) .

					2							2								4
Продифференцируем последнее равенство по x:
		1				1		1			1											1			1					x
		y	y		2x			2		sin x							cosx			4 1 ex e												.
																		1			cosx							ex
												x
Выразим y :	y				xsin x				1 e
																													x
																					2sin x						1 e				.
																		2x							4

3.5. Дифференцирование параметрически заданных функций

Пусть функция задана параметрически уравнениями x x(t), y y(t). Если существуют y (t) и x (t) 0, тогда существует yx , причем

y

yx

t

t

xt

,

xt

.

yx

yxx

Пример 3.10. Найти yx

и yxx

для функции, заданной параметрическими

уравнениями: x lnt,

y t2 1.

Решение.

y

2t

2

2t2

4t

.

t

2t

,

t

4t

2

yx

xt

1/t

yxx

xt

1/t

3

Пример 3.11. Составить уравнение нормали в точке

2

к линии

M0

;2

2

2

y y(x), заданной параметрическими уравнениями:

x 3cost,

y 4sint .

Решение. Найдем

y

4cost

4

ctgt .

t

yx :

yx

xt

3sint

3

Найдем значение параметра t0 , соответствующее точке M0 , из уравнений:

2

3

2

cost

0

3cost0

4

4

,

2

.

Отсюда t0

и kкас

yx(t0)

ctg

.

2

4

3

4

3

2

2 4sint0

2

sint0

2

18

Уравнение нормали: y y			1	x x	или	y 2			3	x	3		2		, или
							2
	0
			kкас.	0			4					2

6x 8y 72 .

3.6. Правило Лопиталя

Пусть	в выколотой окрестности точки a функции f x , g x		− диффе-
ренцируемы,	g x 0 и существует конечный или бесконечный lim		f x	.
	x a	g x

	Тогда, в случае неопределенности				0	или				, справедливо правило Лопиталя:
					0
		lim		f (x)			lim		f (x)		.
				g(x)
		x a					x a g (x)

Пример 3.13. Вычислить пределы, используя правило Лопиталя:

lncosx

ex e x 2x cos3 x

а)

lim

;

б) lim

.

x

x sin x

x 0

x 0

1 x5

lncosx

0

1

( sin x)

(lncosx)

Решение. а). lim

lim

lim cosx

0.

x

x

1

x 0

0

x 0

x 0

б). Имеем неопределенность 0 . Применение правила Лопиталя приведет к

0

громоздким выкладкам. Заметим, что к нулю стремятся только первые множители в числителе и знаменателе. Воспользуемся этим:

	ex e x 2x cos3 x				ex e x 2x		cos3 x			ex e x 2x
lim				= lim	x sin x	lim			= lim	.
x 0	x sin x 1 x5			x 0		x 0		1 x5	x 0	x sin x

После такого упрощения применим правило Лопиталя:

ex e x 2x

0

ex e x 2x

ex

e x 2

0

(ex e x 2)

lim

x sin x

=

lim

x sin x

= lim

lim

x 0

0

x 0

x 0

1 cosx

0

x 0

(1 cosx)

e

x

e

x

0

(e

x

e

x

e

x

e

x

lim

lim

)

lim

2.

sin x

0

cosx

x 0

x 0

(sinx)

x 0

Здесь пришлось применить правило Лопиталя три раза.

Для раскрытия неопределенностей вида 0 , , 1 , 0 их сводят

к неопределенностям вида	0			или				и затем применяют правило Лопиталя.
		0

Пример 3.14. Вычислить пределы, используя правило Лопиталя:

а) lim [( 2arctg x) x];	б) lim		x		1
								;
x	x 1	x 1				ln x

	Решение. а). lim [( 2arctg x) x] [0 ]	lim	2arctgx		0
			1/ x			0
	x	x

19

lim	( 2arctgx)		lim	2/ 1 x2		2	lim	x2		2.
x			x	1/ x	2		x 1 x		2
	1/ x

б). Имеем неопределенность [ ], поэтому правило Лопиталя неприменимо. Преобразуем функцию, приводя к общему знаменателю; получим неопреде-

0

ленность и применим правило Лопиталя:

0

lim

x 1

x

1

[ ]=lim

xln x x 1

0

lim

lim

(x 1) ln x

0

x 1 x 1

ln x

x 1

x 1

ln x x 1/ x

1

ln x

0

(ln x)

lim

lim

ln x (x 1)/ x

0

x 1 ln x 1 1/ x

x 1

lnx 1 1/ x

(xlnx x 1)
((x 1) lnx)
lim	1/ x				1	.
	1/ x 1/ x2
x 1				2

В данном примере пришлось применить правило Лопиталя два раза.

Пример 3.15. Вычислить предел lim		x sin x		.
x			x			f (x)
Решение. Имеем неопределенность			. Вычислим		lim		lim	1 cos x	.
						g (x)		1
					x		x

Выберем две последовательности:

x			2 n	при n ,	lim (1 cosx	) 1 ;
n	2				n	n
xn 2 n				при n ,	lim (1 cosxn) 0.
					n
Значит, lim(1 cosx)	не существует. Таким образом, для вычисления искомого
x

предела правило Лопиталя неприменимо. Вычислим предел другим способом:

					x sin x		1				1 .
				lim		lim 1			sin x
					x
				x		x	x
Мы воспользовались тем, что произведение										бесконечно малой при x
функции	1		на ограниченную функцию sin x				есть бесконечно малая функция и,
	x
значит, lim			1	sin x 0.
x x								x
Пример 3.16. Вычислить предел						lim 2 х tg				.
								2

x 1

Решение. Имеем неопределенность 1 . Воспользуемся основным логариф-

мическим тождеством lim 2 х tg 2x lim e tg 2x ln 2 x

x 1 x 1

. Вычислим предел показа-

теля степени, применяя правило Лопиталя:

lim	ln 2 x		0			lim	ln(2 x)
				0
x 1 ctg x/2						x 1	ctg x/2

limtg x ln 2 x 0

x 1	2
lim	1/ 2 x		2	.
	1/sin2 x/2 /2
x 1

Поэтому искомый предел равен e2/ .

20