MatAn_practice

3.7. Формула Тейлора

Пусть f (x) непрерывна и имеет непрерывные производные до n-го порядка включительно в окрестности точки x0 . Тогда справедлива формула Тейлора n го порядка

f (x) f (x

)

f (x0)

(x x ) ...

f (n)(x0)

(x x

)n R (x)

.

0

1!

0

n!

0

n

Остаточный член формулы Тейлора может

быть записан в форме Пеано:

R (x) o((x x )n) , где функция

o((x x

)n) − бесконечно малая функция более

n

0

0

высокого порядка, чем (x x )n .

0

Если в окрестности точки x

0

существует

f (n 1)(x), то остаточный член мо-

жет быть записан в форме Лагранжа:

точка, лежащая между x и х0 .

Пример 3.17. Разложить функцию

	R (x)	f (n 1)(c)	(x x		)n 1, где с некоторая
		(n 1)!
	n			0
	f (x) x3	2x2 3x 5		по степеням (x 2).

(x) 3x

2

f

(4)

(x) 0.Отсюда

Решение. f

4x 3 ; f (x) 6x 4;

f (x) 6;

f (2) 11; f

(2) 7;

8;

f

f

(4)

(2) 0.

f (2)

(2) 6;

Следовательно, по формуле Тейлора третьего порядка

x3 2x2 3x 5 11 7(x 2)

8

(x 2)2

6

(x 2)3 R x .

f 4 c

2!

3!

3

Остаточный член R

3

x

x 2 4

0. Таким образом,

4!

x3 2x2 3x 5 11 7(x 2) 4(x 2)2 (x 2)3 .

Пример 3.18. Вычислить

1

с точностью до 0,01.

4 e

Решение. Используем разложение

xn

f x ex 1 x

x2

x3

...

R (x)

при x

1

.

2!

3!

n!

n

4

Запишем остаточный член в форме Лагранжа:

										R (x)									f (n 1)(c)									xn 1							ec xn 1					.
												n									(n 1)!														(n 1)!
									Rn 1/4													ec 1/4 n 1
При x 1/4 получаем:																																		, где c 1/4, 0 . Тогда
																									(n 1)!
	Rn 1/4				e0
							.		Подставив в это неравенство n 1, n 2, , получим
				4n 1
					(n 1)!							1								1				;							1							1	0,01.
						R		1																		R	2
									4			2 2!					32														43 3!						384
Таким образом, для заданной точности достаточно трех слагаемых
												1			1						1				1/4 2								25				0,78.
																				4													32
									4				e											2!

21

	Пример 3.19. Вычислить lim	sin x x 3 1 x2	.
		x3
	x 0

Решение. Так как знаменатель равен х3, то достаточно найти разложение числителя до о х3 . Поэтому для первого слагаемого воспользуемся разложением

sin x x

x3

x5

... ( 1)k 1

x2k 1

o x2k ;

при k 1

имеем

sin x x

x3

о x3

.

3!

5!

2k 1 !

6

Для второго слагаемого воспользуемся разложением

1 x 1 x ...

1 ... n 1

xn o xn .

n!

Положим n 1,

1/3, заменим x на (−x2 ) и учтем, что x o x2 o x3 . Тогда

1/3

1

1

x 3 1 x2 x 1 x2

x

1

x2 o x2

x

x3 o x3 .

3

3

1

1

1

Тогда sin x x 3

1 x2 x

x3 o x3

x

x3 o x3

x3 o x3

,

3

2

6

o x3

sin x x 3 1 x2

1

,

sin x x 3

1 x2

1

.

lim

x3

2

x3

x3

о x3

x 0

2

Здесь мы учли, что lim

0, так как о x3 есть бесконечно малая более вы-

x

3

x 0

сокого порядка, чем x3 .

4.Исследование функций. Построение графиков

При построении графика функции можно использовать следующую схему:

1)найти область определения функции;

2)проверить функцию на четность, нечетность, периодичность;

3)найти асимптоты графика функции;

4)исследовать функцию на монотонность и экстремум;

5)исследовать график функции на выпуклость, вогнутость; найти точки перегиба;

6)найти (если возможно) точки пересечения с осями координат.

Не всегда нужно точно следовать этой схеме. Отметим следующие случаи: а) часто для построения графика функции достаточно пунктов 1-4 (краткая схема); б) если функция определена при x 0, то не надо проверять ее четность;

в) если функция определена на конечном интервале, то не надо искать ее невертикальные асимптоты; г) если функция четная (или нечетная), то достаточно исследование провести

для x 0, а при построении графика функции учесть, что он симметричен относительно оси Oy для четной функции (относительно начала координат для нечетной функции); д) если функция периодическая, то достаточно исследование провести на про-

межутке с длиной, равной периоду.

Пример 4.1. Исследовать функцию y x3 4 и построить её график. x2

22

x 0 и x 2

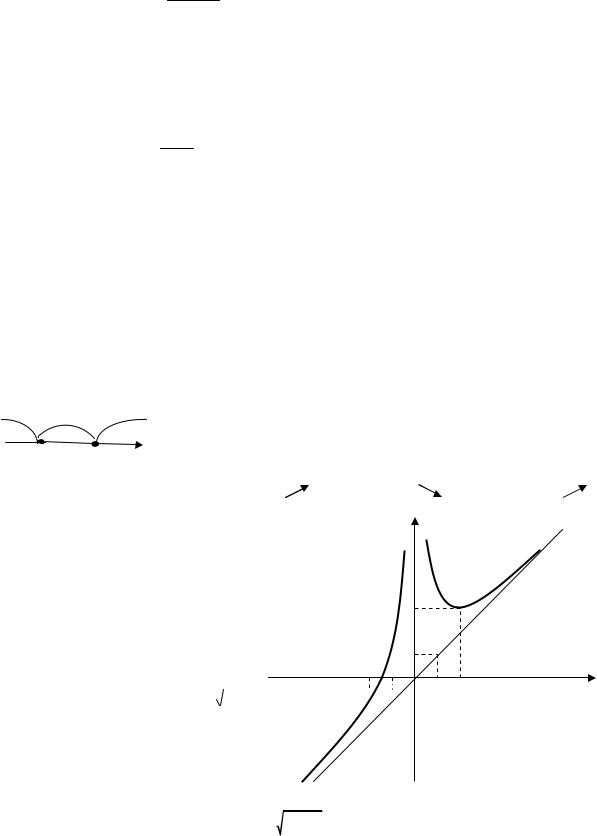
Решение.

1.Область определения функции − вся числовая ось Ох, за исключением точ-

ки x 0, то есть D(y) ( ; 0) (0; ).

2.Функция не является четной или нечетной

x3 4

y( x) ; y( x) y(x); y( x) y(x) x2

3. Найдем асимптоты.

а). Точка разрыва x 0, причем lim y , следовательно, x 0 (ось Оу) является

x 0

вертикальной асимптотой графика.

б). Найдем наклонную асимптоту y kx b :

k lim f (x)

x x

b lim( f (x)

x

lim	x3 4		1;
x x3
	x3 4						4
kx) lim					x	lim			0.
				2				2
			x			x x
	x

Наклонная асимптота имеет уравнение y x .

4. Найдем экстремумы функции и интервалы возрастания и убывания.

4

8

x3 8

y 0

при x 2;

при x 0.

y x

1

;

y

x2

x3

x3

Точки разбивают область определения функции на промежутки ( ; 0), (0; 2), (2; ) . Определим знак производной методом интервалов (рис.4), и в зависимости от него возрастание или убывание функции. Результаты исследования представим в виде таблицы.

+

−

+

x

x

( ; 0)

0

(0; 2)

2

(2; )

0

2

y

+

∞

0

+

Рис.4

y

∞

3

min

5. Найдем

интервалы выпуклости

y

и вогнутости кривой и точки ее пере-

гиба. Так как y

24

0,

то график

y

x

x4

3

всюду вогнут. Точек перегиба кривая

не имеет.

1

6. Найдем точки пересечения гра-

фика с осью Ох:

x3 4

0,

x 3

-2

0 1 2

x

4.

x2

Используя

полученные

данные,

строим график функции (рис.5).

Рис.5

Пример 4.2. Исследовать функцию y 31 x3 и построить её график.

23

Рис.6

y x

Решение.

1.D(y) ( ; )

2.Функция не является ни четной, ни нечетной.

3.Точек разрыва нет и, значит, вертикальных асимптот нет. Найдем наклонные асимптоты y kx b :

3

1 x3

1

3 1 x3 x

k lim

1,

b lim

lim

0 .

x

x

x

x

3 1 x3

2

x 3 1 x3 x2

Итак, наклонная асимптота y x .

4. Исследуем на экстремум и монотонность:

y

x2

;

y 0

при x 0,

y

при x 1.

3 (1 x3)2

Знак производной не меняется, экстремумов нет. Так как

y 0 при всех x, то

функция убывает на всей числовой оси.

5. Исследуем на выпуклость:

y

2x

; y 0

при x 0;

y

при x 1.

3 (1 x3)5

Результаты исследования можно представить в виде таблицы.

x		( ; 0)		0	(0;1)		1	(1; )
y		+		0				+
y				1			0
		вогнута		точка перегиба	выпукла		точка перегиба	вогнута
Точки перегиба имеют координаты (0;1),							(1;0).
6.Точки пересечения с осями координат:									y
если x 0, тоy 1; если y 0, то x 1.
Используя полученные данные, строим гра-
фик (рис.6).									1
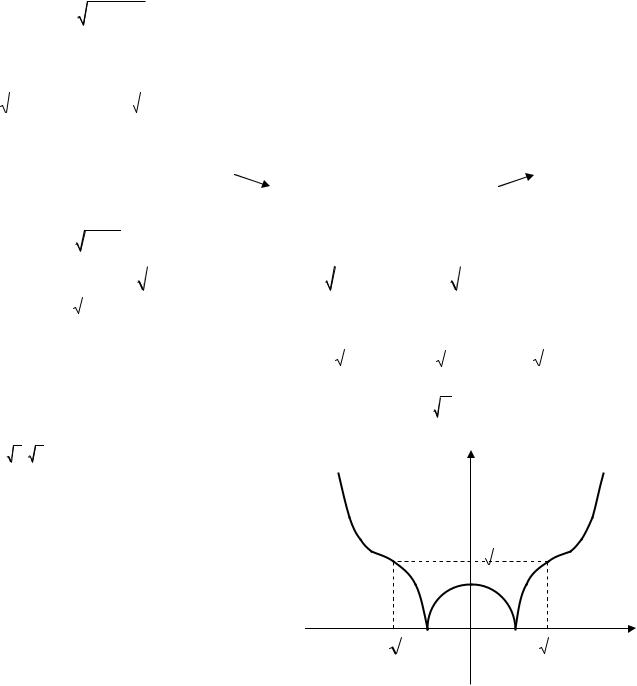
Пример 4.3. Исследовать функцию
			и построить её график.
y 3		1 x2 2						0	1		x

Решение. 1. D(y) ( ; )

2. Функция является четной, так как

y( x) 3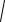(1 ( x)2)2 3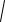(1 x2)2 y(x).

Поэтому построим график при x 0 и отразим его симметрично относительно оси Оу. Исследование функции также проведем только для x 0.

3. Точек разрыва и вертикальных асимптот нет. Найдем наклонную асимптоту y kx b :

24

k lim

y(x)

3

(1 x2)2

x

4/3

,

значит, наклонной асимптоты нет.

lim

lim

x

x

x

x

x

x

4. Исследуем функцию на монотонность и экстремумы.

y

2

1

( 2x)

4x

;

y 0,

если x 0;

y , если x 1.

3 3 1 x2

33 1 x2

x

0

(0;1)

1

(1; )

y

0

−

+

y

1

0

min

5. Исследуем выпуклость графика. Найдем вторую производную

3

1

2

2/3

1 x

2

(1 x

( 2x)x

4

)

4 1 x2 2x2

/3

4

3 x2

y

3

;

3

3 (1 x2)2

3

3 (1 x2)4

9 3 (1 x2)4

y 0,

если x

3, y , если x 1. Определим знаки второй производной, в

зависимости от них – характер выпуклости; результаты поместим в таблицу.

x

0

(0;1)

1

(1;

3)

3

( 3; )

y

4/3

–

–

0

+

3

y

1

0

4

выпукла

выпукла

точка перегиба

вогнута

Точка (

3;3 4) точка перегиба

y

6. Точки пересечения с осями координат:

если x 0, то y 1;

если y 0, то x 1.

Строим график (рис.7).

3

4

Пример

4.4.

Исследовать

функцию

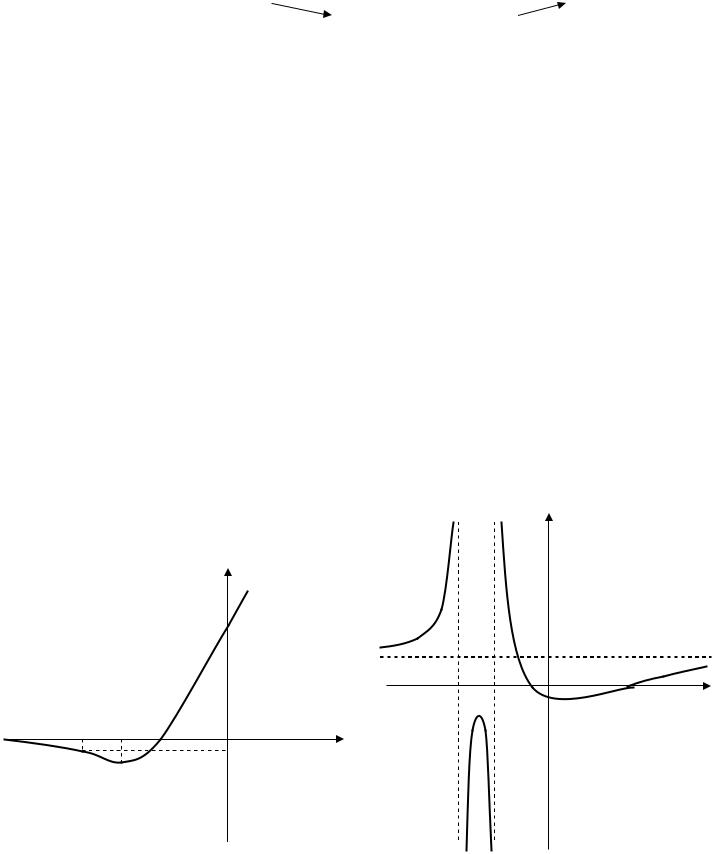
y ex (x 2) и построить её график.

Решение. 1. D(y) ( ; )

x

2. Функция не является четной и не явля-

3 -1

0

1

3

ется нечетной.

3. Точек разрыва нет, следовательно, вер-

Рис.7

тикальных асимптот нет.

Найдем наклонную асимптоту y kx b :

k lim

f (x)

ex

(x 2)

lim e

x

2

0, x

lim

1

, x .

x

x

x

x

x

x

Следовательно,

график функции не имеет асимптоты при x .

Найдем b

только при x :

x 2

(x 2)

1

b lim ( f (x) kx) lim

ex (x 2)

0

lim

lim

lim

0.

x

e

x

x

x

x e

x (e x)

x

Таким образом,

y 0 горизонтальная асимптота при x .

4. Исследуем функцию на монотонность и экстремумы:

y ex(x 2) ex ex(x 3);

y 0

, если x 3.

25

x

( ; 3)

-3

( 3; )

y

–

0

+

y

e 3

min

5. Исследуем выпуклость графика:

y ex(x 4);

y

0, если

x 4.

x

( ; 4)

-4

( 4; )

y

–

0

+

y

2e 4

выпукла

точка перегиба

вогнута

6. Точки пересечения с осями координат: (0; 2),( 2; 0) .

Строим график функции (рис.8).

Пример 4.5. Построить с минимальным использованием математического

аппарата эскиз графика функции

f (x)

x2 3x 4

.

(x 5) (x 3)

1). Функция f (x)

x2 3x 4

x 1 x 4

неопределена при x 5,

x 3.

(x 5) (x 3)

x 5 x 3

Прямые x 5, x 3 являются вертикальными асимптотами.

2). Точки x 1, x 4 − нули функции. Перемена знака происходит при перехо-

де через точки x 5, x 3,

x 1,

x 4.

3). Так как

lim f x 1, то прямая

y 1 является горизонтальной асимптотой

x

графика функции

f (x) при x .

4). Найдем ординату точки пересечения графика с осью Oy :

f (0) 4/15.

Построим схематично график функции f (x)

(рис.9).

y

y

y

f (x)

2

1

5

- 3 -

-

0

4

x

-4 -3

-2

0

x

2e 4

e 3

Рис.8

Рис.9

26

5. Неопределенный интеграл

Функция F x – некоторая первообразная для функции			f x , если F x f x .
Множество всех первообразных F x C функции		f x	называется неопреде-
ленным интегралом этой функции и обозначается		f (x)dx:
	f (x)dx F(x) C	,	(5.1)

Для вычисления неопределенных интегралов прежде всего следует знать свойства неопределенных интегралов и таблицу интегралов.

5.1. Таблица основных интегралов

1.

u du

u 1

C,

( 1);

du u C,

du

2

.

u

1

u

2.

du

ln|u| C .

u

3.

audu

au

C,

(a 0,

a 1),

eu du eu C..

lna

4.

sinu du cosu C,

shudu chu C.

5.

cosudu sinu C ,

chudu shu C

6.

du

tgu C .

2

cos

u

7.

du

ctgu C .

2

sin

u

8.

du

ln

tg

u

C ln

1

ctgu

C .

2

sinu

sinu

9.

du

u

C ln

1

+tgu

C .

ln

tg

4

cosu

cosu

2

10.

du

1

u

C,

(a 0).

arctg

u2 a2

a

a

11.

du

1

ln

u a

C,

(a 0).

u

2 2

2a

u a

a

12.

du

arcsin

u

C,

(a 0).

a2 u2

a

13.

du

C .

ln

u

u2 a2

u2 a2

Рассмотрим отыскание неопределенного интеграла с помощью свойств интегралов, таблицы интегралов и алгебраических преобразований.

Пример 5.1. Найти интегралы 1) (3 x2)2dx ;

2)

x2

x 2

dx; 3)

x2

dx.

3

1 x

2

6x3

x5

x

Решение. 1) (3 x2)2dx 9 6x2 x4 dx 9x

C 9x 2x3

x5

C ;

3

5

5

27

2)

x2

x 2

1

5

x 4

1

C ;

dx

x

dx ln

x

C ln

x

3

4

x

x

4

4x

x2

x2 1 1

1

3)

dx

dx 1

dx x arctg x C ;

1 x

2

1 x

2

1 x

2

Примеры для самостоятельного решения

Найти интегралы: 1.

du

,

2.

dx

, 3.

dt

,

4.

2x 3x dx.

4 u2

x2 4

3sint

Ответы. 1.arcsin

u

C ,

2. ln

C , 3.

1

t

C ,

4.

2x

3x

C.

ln

tg

x

x2 4

2

3

2

ln2

ln3

5.2. Метод подведения под знак дифференциала

Способ основан на применении свойств дифференциалов:

d x x dx;

d x d( (x) C);

d (x)

1

d(C (x)).

C

Пример 5.2. Найти интегралы

2x

dx

x dx

tg x

1)

;

2)

;

3)

dx ;

4)

4 ln x

dx ;

5)

dx;

5

cos2 x

x

4x 1

1 3x

1 x2

6)

cos

1

dx;

7)

arctgx

4 2

dx;

8)

sin

x cosx dx

;

2x 3

dx .

x

9)

2

x

1 x

cos2 x 3

1 x2

Решение:

d 1 3x 1 1 3x

1/2

1)

dx 1 d 3x

1 1 3x

2

C 2 1 3x C ;

1

3

3

3

1/2

3

1 3x

1 3x

2)

x dx

1

d(x2)

1

d

(1 x2

)

1

1 x2 4/5

5

5

C ;

C

(1 x2)4

5 1 x2

2

5 1 x2

2

5 1 x2

2

4/5

8

3)

tgx

dx

tgx

dx

tgx d(tgx)

tg2

x

C ;

2

2

x

2

cos

x

cos

4 ln x

1/2

2

3/2

4)

dx

4 ln x d(ln x) 4 ln x

d(4 ln x)

4 ln x

C ;

x

3

5)

2x

1

2x ln2

1

d 2x

1

2x 1

;

dx

dx

ln

C

4

x

ln2

2

2x

ln2

2

2x

2

x

1

1

1

1

2ln2

cos

1

cos

1

x

x

6)

cos

x 1 d(

x) 2 sin

x C ;

dx 2

dx 2

x

2

x

x

arctg x 4 2

2

arctg x 4 3

7)

dx arctg x 4

d(arctg x)

C ;

1 x

2

3

2

sin

x cos x

dx

cos x d

cos x

1

d

(cos

x 3)

8)

cos2 x 3 C ;

cos2 x 3

cos2 x 3

cos2 x 3

2

28

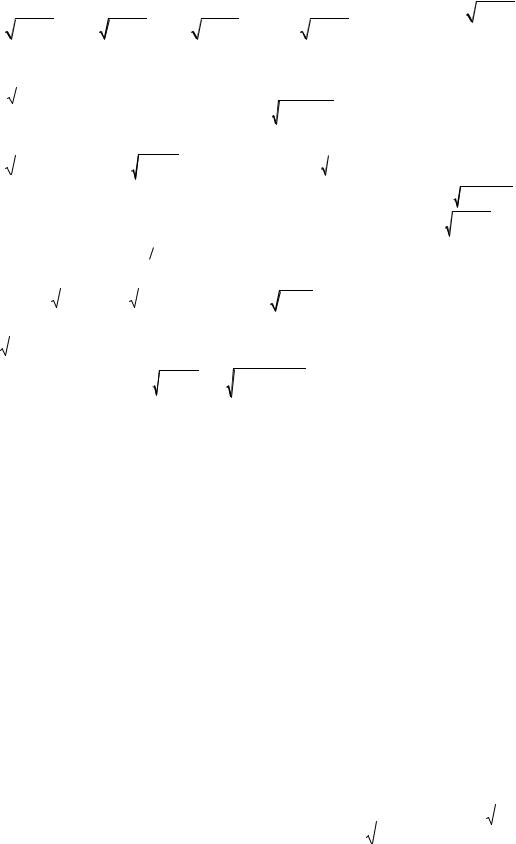
9)						2x 3								dx										2x																	3							dx											d			1 x2
																															dx																																					3arcsin x 2 1 x2										3arcsin x C.
								1 x2															1 x2																1 x2																						1 x2
																												Примеры для самостоятельного решения
1.															dx .					2.							sin(7x 3)dx .																3.																	dx						.
									2x 7
																																																									1 25x2
4.					x 5x3									dx .						5.								cosx									dx.									6.																	dx							.
																																																												2
							1 x4																				3 sin2 x																												cos						x 1 tg x
																													x
									dx																																																															2x arcsin x
7.											.									8.							e dx									.								9.									e x3							x2dx.									10.									dx .
																												2x
																																																																										1 x2
					xln x																						e				4
Ответы. 1.																		1	2x 7 3 2 C.																								2.									1	cos(7x 3) C .																3.		1		arcsin5x C .
		1															3								5																									7																					5
4.				ln						x2							1 x4										1 x4										C.							5. 3 3													sin x						C .
	2																						2																										1									ex
6.	2															C.						7. ln							ln x					C.									8.								arctg										C .
							1 tgx
				1			e x3 C .																																			2				2							2
																																														arcsin x 3
9.																				10.							2 1 x2																																		C .
			3																																						3
																							5.3. Метод интегрирования по частям
			Пусть функции u x и v(x)																																								дифференцируемы. Тогда справедлива формула
																																																		udv uv vdu																			.									(5.2)

Данная формула применяется в случаях, когда подынтегральное выражение можно представить в виде произведения двух множителей u и dv, причем по виду функции dv легко можно восстановить функцию v, и вычисление интеграла vdu является более простой задачей, чем вычисление интеграла udv .

Укажем, как выбирать множители u и dv в некоторых случаях:

1) в интегралах вида P(x)e xdx, P(x)sin xdx, P(x)cos xdx, где P(x) мно-

гочлен, в качестве u выбираем многочлен P(x), чтобы понизить его степень; 2) в интегралах вида P(x)ln xdx, xarctgxdx, arcsin xdx за “u” следует взять функции ln x, arctgx, arcsin x. В противном случае трудно восстановить функцию v по её дифференциалу.

	Пример 5.3. Найти неопределенные интегралы:
	1) xcosxdx;	2) xln xdx; 3) arctgxdx;	4)	x arctgx			dx ;	5)
									a2 x2	dx .
					1 x2

Решение. 1) xcosxdx I . Используя рекомендации, положим u x, dv cosxdx.

Тогда du dx, v sin x. Используя формулу (5.2), имеем:

I xcosxdx xsin x sin xdx xsin x cosx C.

29

u ln x du

dx

x2

x2

x2

x2

2) xln xdx

x

lnx

dx

ln x

C .

2

dv xdx v xdx

x

2

2

x 2

4

2

u arctgx du

3) arctgxdx

dv dx v x

4) x arctgxdx I . Положим u

1 x2

dx

dx

1 x2

x arctgx

x

1 x2

1

d(x2 1)

1

2

x arctgx

x arctgx

ln(x

1) C.

2

1 x

2

2

arctgx,

dv

x dx

; тогда

1 x2

1

dx

,

v

x dx

1

d(x2 1)

1

(x2 1)

2

.

du

x2 1

2

1 x

1 x2

2

1 x2

2

1

2

x arctgx

dx

Таким образом,

I

dx arctgx

1 x2

1 x2

2

1 x2

1 x

dx

x

C .

arctgx

1 x2

arctgx

1 x2 ln

1 x2

1 x2

x

5)

a2 x2

dx I .

Положим u

a2 x2

,

dv dx.

Тогда du

dx, v x .

Используя формулу (5.2) интегрирования по частям, получим

a2 x2

x2 dx

a2 x2 a2

I a2 x2 dx x a2 x2

x a2 x2

dx

a2 x2

a2 x2

dx

arcsin

x

.

x a2

x2

a2 x2dx a2

x a2 x2

a2 x2dx a2

a2 x2

a

Таким образом, имеем:

x

a2 arcsin

x

.

I x

a2

x2 I a2 arcsin

2I x a2

x2

a

1

x

a

Тогда I

x a2

x2 a

2 arcsin

. Мы получили одну из первообразных. Чтобы

a

2

записать множество первообразных, нужно добавить произвольное число C:

1

x

a2 x2dx

x

a2

x2 a2 arcsin

С .

2

a

2

x

Пример 5.4. Найти интеграл

cos

dx.

3

sin

x

Положим

u cosx, dv

cosx

dx

d sin x

. Здесь такой выбор u

и dv менее оче-

sin3 x

sin3 x

виден, чем в предыдущих примерах. В выражение для

dv мы включили cosx ,

чтобы получить d sin x

и легко вычислить v:

v

dv

d(sin

x)

sin 2 x

.

3

sin

x

2

30