MatAn_practice

b		b
f(x)dx F(x)			,	f(x)dx F(x)			.

Пример 7.1. Вычислитьнесобственныеинтегралыили установитьихрасходимость:

dx

2xdx

dx

dx

1)

,

2)

, 3)

,

4)

, 5) xsin xdx.

3/2

2

2

2x 2

x2

e x(ln x)

x 1

1 x

1

x

0

Решение. Воспользуемся обобщенной формулой Ньютона-Лейбница

f (x)dx F(x)|a F( ) F(a):

a

d x

d (ln x)

1

1

1)

2

2 0

2;

3/2

3/2

1/2

e

1/2

e

x (ln x)

e

(ln x)

(ln x)

(lne)

a

2)

2xdx

2xdx

2xdx

; интеграл расходится, т.к.

2

2

2

x

1

x

1

a

x

1

d x2 1

2xd x

ln x2 1

a

a

a ;

x2 1

x2 1

d

1/ x

dx

dx

ln 1/ x 1/ x2 1

3)

ln 1 2

;

2

2

2

2

1 x x

1

1 x

1 1/ x

1

1/ x

1

1

dx

dx

4)

arctg(x 1)|

;

2

2x 2

(x 1)

2

x

1

2 2

5)

u x,

du dx

xsin xdx

dv sin xdx,

v cosx

xcosx|0 cosxdx ;

0

0

интеграл расходится, т.к. не существует предел lim(xcosx).

x

Пример 7.2. Вычислить площадь фигуры, ограничен-

	ной линиями y	1	, x 1 и осью абсцисс.
		x2(x 1)

Решение. Построим фигуру, ограниченную данными линиями (рис. 17). Площадь S полученной фигуры равна:

dx

(1 x) x

dx

dx

S

dx

x

2

(x 1)

x

2

(x 1)

x

2

1

1

1

1

x(x 1)

y

1/2

0	1	x
		Рис. 17

1

dx

(x 1/2) 1/2

x

1

1 ln2.

1

1 ln

1 limln

ln

x

1

(x 1/2)2 1/4

(x 1/2) 1/2

1

x

x 1

2

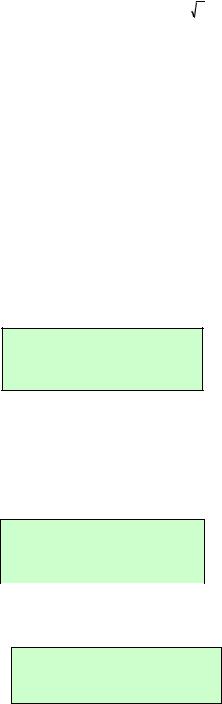
Пример 7.3. Найти площадь фигуры, заключенной

y

между линией y xe x2 и ее асимптотой.

1

Решение. Прямая y 0 является горизонтальной

-1

асимптотой графика функции y xe x2 , т.к.

0 1

x

51	Рис. 18

		lim xe x2				lim			x			0.
		x					x ex2					и y xe x2
Построим фигуру, ограниченную линиями y 0																					(рис. 18). Очевидно,
что площадь S всей фигуры равна 2S1, где
		2		1			2					1				2					1
S1 xe x		dx			e x		d( x2)							e x				|0				.
				2									2								2
0					0
Тогда, S 2S1 1.
Примеры для самостоятельного решения
1. Вычислить несобственные интегралы или установить их расходимость:
	x2dx						dx
а)			,		б)				,		в) e xdx.
	3 2						x ln x
0	(x	1)				e						0							1
										Ответ: а)										, б) расходится, в) 2.
																		3

	2.	Найти площадь фигуры, ограниченной линиями y x2, y			1	и осью абсцисс.
					x2
						Ответ: 8/3.
			1
	3.	Фигура ограничена линиями y		, x 1 (x 1) и осью OX . Найти объем тела,
			x3			Ответ: /5.
	образованного при вращении этой фигуры вокруг оси OX .

3.2. Несобственные интегралы второго рода

Для функции f x , неограниченной вблизи точки x b, несобственный ин-

теграл определяется следующим образом:

b

b1

	f(x)dx	lim		f(x)dx.
		b b 0
a		1	a

Если этот предел существует и конечен, то несобственный интеграл называется сходящимся, в противном случае несобственный интеграл называется расходящимся.

Аналогично для функции f x , неограниченной вблизи точки x a, несоб-

ственный интеграл определяется следующим образом:

b b

		f(x)dx	lim		f(x)dx.
			a a 0
	a		1	a1
Для функция f x неограниченной вблизи точки							x c	a c b несоб-

ственный интеграл определяется равенством

b c b

f(x)dx f(x)dx f(x)dx .
a	a	c

52

Если каждый из интегралов в правой части равенства сходится, то несобственный

b
интеграл f(x)dx	называется сходящимся, в противном случае – расходящимся.
a
Для функции	f x , неограниченной вблизи								точки x b, имеем аналог
формулы Ньютона-Лейбница:
		b			b	,		где F b =	lim F(x).
		f(x)dx F(x)
		a			a			x b 0
Аналогично для функции f x , неограниченной вблизи точки x a,
			b				b	, где F a = lim F(x).
			f (x)dx F(x)
			a				a		x a 0

Пример 7.4. Вычислитьнесобственныеинтегралыили установитьихрасходимость:

e		dx			e	dx			5		x2dx	1		3x2		2
1)					, 2)			,	3)				, 4)				dx.
							2
	x		ln x			x(ln x)					(x 3)(5 x)			3 x5
1				1					3				1

Решение. Во всех предложенных интегралах на интервалах интегрирования существуют особые точки, в которых подынтегральные функции неограничены, поэтому интегралы являются несобственными. Для вычисления интегралов будем использовать обобщенную формулу Ньютона-Лейбница.

1). В первом интеграле особая точка x 1																																							ln1 0 . Вычислим интеграл:
											e																e
																	dx												d		(ln x					)			2												|1e 2.
																																														ln x
													x					ln x													ln x
										1																1
				e		dx					e			d(ln x)																1					e
2). Интеграл																																					, т.е. интеграл расходится.
					x	(ln x)		2						(ln x)									2												1
		1								1																			ln x
																																			5										x2dx
3). Подынтегральная функция интеграла																																																											имеет две особые точки
																																									(x 3)(5 x)
																																			3
x 3, x 5, поэтому представим интеграл в виде суммы двух интегралов:
5		dx			4				dx							5														dx															4 d x 4																		5 d x 4
																											x2
3		(x 3)(5 x)			3		x2 8x 15 4																							8x 15														3						1 (x 4)2													4		1 (x 4)2
					arcsin x 4												4				arcsin x 4																	5
																																												0																0				.
																	3																					4																					2
																																															2
4). Точка x 0					является особой для функции																																									3x2 2										и расположена внутри от-
																																															3 x5
резка 1, 1 . По определению
								1			3x				2						2					0				3x		2					2							1				3x				2				2	dx .
																						dx																		dx
									1			3 x5															1				3 x5													0						3 x5

53

0		2				2 3 1						0					1	3x2 2
Интеграл					dx								, т.е. расходится, поэтому									dx	также
	3					2		3				1						3
		x	5						x	2									x	5
1																	1
расходится.																							y
Пример 7.5. Вычислить площадь фигуры, ограниченной линиями
					x 0, x 1,								y 0, y		1	.
															1 x2

Решение.Построимфигуру,ограниченнуюзаданнымилиниями(рис.19). Площадь этой фигуры вычисляется с помощью несобственного ин- 1 теграла (x 1 особая точка):

1	1		dx			arcsin x|10		.
S ydx
							2
			1 x	2
0	0

Пример 7.6. Фигура ограничена осью абсцисс и линия-

	ми y x3,	y	1	. Найти объем тела, образованного при
			x3
	вращении этой фигуры вокруг оси OY .

Решение. Построим фигуру, ограниченную данными линиями (рис. 20). Так как фигура симметрична относительно начала координат, то искомый объем V равен удвоенному объему, получаемому при вращении части

	фигуры при	x 0 .			Разрешим уравнения линий относи-
	тельно x: x	3		, x			1	. Рассмотрим две фигуры.
			y
	1	2			3		y

0	1 x
	Рис. 19

y
1
-1		x
0	1
-1

Рис. 20

Первая фигура ограничена линиями x 0,	y 1,	x 3	y	y [0,1] . При вращении
		1

этой фигуры вокруг оси OY получим тело, объем которого

1 V1 x12

0

1

(y)dy y2/3dy 35 .

0

Вторая фигура ограничена линиями x														1				, y 0, y 1, x 0				y [0;1] . При
									2		3					y
вращении этой фигуры вокруг оси OY получим тело, объем которого равен
						1					1						dy			3 .
			V2 x22(y)dy
																	2/3
						0					0						y
Тогда объем тела,	получаемого при вращении вокруг оси OY																					фигуры, ограни-
ченной линиями x	3		, x				1	и осью абсцисс (x 0) , равен
		y
1	2			3			y
				V V V 3							3								12		.
											5
						2			1							5
Объем тела, получаемого при вращении вокруг оси OY всей фигуры, равен
								V	2V	24						.
								oy			5

54

Примеры для самостоятельного решения

1. Вычислить несобственные интегралы или установить их расходимость:

2

xdx

e

dx

5

dx

1

x

1

а)

;

б)

; в)

; г)

dx.

xln x

x

2

1

x 1

1

1

4x

1

5 x3

	Ответ: а)		8		;		б) расходится;			в) расходится; г)			10	.
			3
												7
2.	Фигура, ограниченная линиями y		1			,	x 1 (x 1) и осью OX , вращается во-
			x3
												Ответ: 2 .
круг оси ординат. Найти объем тела вращения.
3.	Найти площадь фигуры, ограниченной линиями y								1		, x 1,	x 2, y 0.
									x 1

Ответ: 2 .

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Берман Г.Н. Сборник задач по курсу математического анализа. М.: Наука, 2002г., 443 с.

2.Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч.1. М.: Изд-во «Оникс»,2004. 304 с.

3.Задачи и упражнения по математическому анализу для втузов/ под ред. Б.П Демидовича. М.: «Изд-во Астрель», 2003. 495с.

4.Письменный Д.Т. Конспект лекций по высшей математике. Ч.1. М.: Айрис-

пресс, 2003. 288 с.

5.Сборник задач по математике для вузов. Линейная алгебра и основы математического анализа/ под ред. А.В. Ефимова, Б. П. Демидовича. М.: Наука, 1996. 464 с.

6.Краснов М.Л. Вся высшая математика./М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. Ч.1. М.: Эдиториал УРСС, 2004. 352 с.

7.Краснов М.Л. Задачи и примеры с подробными решениями./М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. Ч.1. М.: Эдиториал УРСС, 2004. 172 с.

8.Черненко В.Д. Высшая математика в примерах и задачах. / В. Д. Черненко. С-Птб.: Политехника, 2003. 703 с.

9.Минькова Р.М. Математический анализ. Часть 1. / Р.М. Минькова. Екатеринбург: УГТУ УПИ, 2006. 80 с.

55

Учебное издание

Наталия Владимировна Чуксина, Ревекка Максовна Минькова

Руководство к решению задач по математическому анализу

Редактор Н.П. Кубыщенко

Подисано в печать 16.08.2013			Формат 60 84 1 16
Бумага типографская	Офсетная печать		Усл. печ.л.	3.65
Уч.-изд. л. 3,4	Тираж	Заказ	Цена С

Редакционно-издательский отдел УрФУ 620002, Екатеринбург, ул. Мира, 19

56