Лекции Стечкина по матану

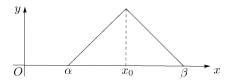
Рис. 5.1. Гладкость функции.

и будет выполняться условие: k0 − ε <	y0	< k0 + ε . Следователь-
	x0
но, график функции при |x − x0| <	заключен между прямыми с

тангенсами углов наклона k0 −ε и k0 + ε , проходящими через точку (x0, y0) (рис. 5.1). В этом случае говорят, что функция является

"гладкой" в точке M0 .

Определение. Пусть функция ϕ(x) определена на отрезке [a, b] и для всех точек x, x′ [a, b] удовлетворяет условию

|ϕ(x) − ϕ(x′)| ≤ K |x − x′|α ,

где 0 < α ≤ 1 . Тогда говорят, что функция ϕ(x) удовлетворяет на отрезке [a, b] условию Липшица порядка α с константой K. Класс функций, удовлетворяющих условию Липшица порядка α с константой K, будем обозначать LipK α .

Заметим, что из условия Липшица любого порядка α следует

непрерывность, но не наоборот.

√

Пример 1) . Функция y = 1 − x2 является непрерывной на от-

резке [−1, 1] , но не удовлетворяет условию Липшица порядка 1.

Теорема. Если функция дифференцируема в точке, то она непрерывна в этой точке и удовлетворяет условию Липшица порядка

1.

Д о к а з т е л ь с т в о. Пусть функция y = f (x) определена для x (α, β) , x0 (α, β) и существует f ′(x0) . Тогда a > 0 K

1) Функция LN1x , доопределенная нулем в точке x = 0 , дает пример непрерывной на [0, 0.5] функции, не принадлежащей классу LIPK α ни при каком α . (Ред.)

91

dy dx

| x0| ≤ a			¯	y0	¯	≤ K , откуда	|	y0| ≤ K | x0| (| x0| ≤ a) ,
что и			¯		¯
	означает, что выполняется условие Липшица порядка 1. Из
		Липшица следует непрерывность функции в точке x								.
условия			¯		¯				0

Заметим, что из непрерывности функции ее дифференцируемость не следует.

Пример. Функция y = y0 − |x − x0| (рис. 5.2) непрерывна в точке x0 , но не является дифференцируемой в точке x0 (не имеет производной в точке x0 ).

Рис. 5.2. Функция не имеет производной в точке x0 .

Теорема. Пусть функция имеет производную в точке x0 . Тогда она дифференцируема в этой точке.

Д о к а з а т е л ь с т в о. Пусть существует f ′(x0) = lim							y0 .
						x0→0	x0
Значит f ′(x			y0
	0	) =		+ o(1) (Δ x	0 →	0) . Тогда
			x0

f ′(x0) x0 = y0 + o(Δ x0) (Δ x0 → 0)

и

y0 = f ′(x0)Δ x0 + o(Δ x0) (Δ x0 → 0) .

Это значит, что приращение функции имеет главную линейную часть, т. е. дифференциал в точке d y = f ′(x0) x0 , и функция дифференцируема в точке x0 .

Рассмотрим функцию y = x . Приращение этой функции в точке x0 равно x0 , т. е. d x = x . Будем обозначать приращение

x независимой переменной d x . Тогда d y = f ′(x) d x и f ′(x) =

– обозначение Лейбница для производной – отношение дифференциала зависимой переменной к дифференциалу независимой переменной.

92

§ 22. Правила дифференцирования

22.1. Дифференцирование – линейная операция

Пусть функции f и	g дифференцируемы в точке x . Тогда для
	′	′
любой постоянной α	(αf ) = αf ′	и (f + g) = f ′ + g′ . Это следует

из соответствующих свойств пределов.

Лекция 20 (15.11.67)

22.2.Геометрический смысл дифференцируемости

Определение. Наклонная прямая Y = y0 +A(x−x0) , проходящая через точку M0 (x0, y0) , называется касательной к графику функции в точке x0 , если разность ординат точек графика и прямой

при x → 0 есть y − Y = o(Δ x) .

Теорема (геометрический смысл дифференцируемости).

Функция y = f (x) дифференцируема в точке x0 тогда и только тогда, когда у графика функции имеется касательная в этой точке. При этом уравнение касательной имеет вид

Y− y0 = f ′(x0)(x − x0) .

До к а з а т е л ь с т в о. Пусть функция дифференцируема в

точке x0 . Тогда y − y0	= f ′(x0)Δ x0 + o(Δ x0) и, значит, прямая
Y = y0 + f ′(x0)(x − x0)	– касательная, так как y − Y = o(Δ x) .

Обратно, если для какой-нибудь прямой Y = y0 + A(x − x0) выполняется условие y − Y = o(Δ x) , то

y − y0 = A x0 + o(Δ x0) ,

следовательно, функция дифференцируема и A = f ′(x0) . Отметим, что d y = Y −y0 – приращение касательной (рис. 5.3). Прямая, проходящая через точку M0 (x0, y0) и ортогональная

касательной называется нормалью функции в этой точке. Уравне-

ние нормали функции

1

Y − y0 = −f ′(x0) (x − x0).

93

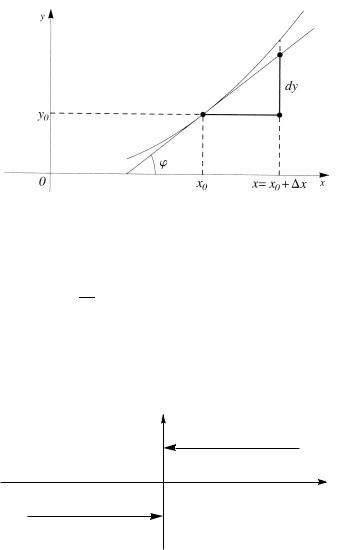
Рис. 5.3. Геометрический смысл дифференцируемости.

22.3. Механический смысл производной

Пусть точка движется по оси, s(t)

– перемещение точки от начала

движения. Тогда

s

= v

– средняя скорость за время

t . Если

t

s

устремим t → 0 , то получим

lim

– скорость дви-

t = v(t0)

t 0

→

жения в момент времени t0 . Тогда ds = v(t0)Δ t

– длина отрезка

пути, который точка прошла бы от точки s(t0) = s0 , если бы стала

двигаться с постоянной скоростью v(t0) .

y

x0 =0

x

Рис. 5.4. f (x) = sign x ,

f ′(0) = + .

∞

Замечание. Если

lim

0

y

= +

∞

(или lim

y

=

−∞

), то обо-

x

→

x

x 0

x

→

94

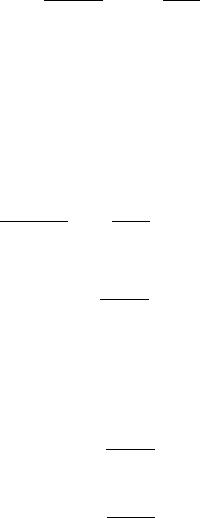
значаем f ′(x0) = +∞ (или f ′(x0) = −∞ ) и считаем, что x = x0

– касательная к графику функции в точке x0 (см. примеры на

рис. 5.4 и рис. 5.5).

√

Рис. 5.5. f (x) = 3 x , f ′(0) = +∞ .

22.4. Правила дифференцирования

Теорема. Пусть функции u = u(x) и v = v(x) определены в окрестности точки x и дифференцируемы в этой точке. Тогда их сумма, разность, произведение, а если v(x) =6 0 , то и частное

u(x) , дифференцируемы в точке x и верны формулы

v(x)

′

v′(x);

1) (u(x)

±

v(x)) = u′(x)

±

′

2) (u(x)

·

v(x)) = u′(x)v(x) + u(x)v′(x);

′

u′(x)v(x) − u(x)v′(x)

3)

u(x)

=

µ v(x)

¶

v2(x)

Д о к а з а т е л ь с т в о. Зададим приращение переменной, при этом функции u и v получат

(v(x0) =6 0).

x = h независимой приращения u и

v.

1)Пусть f (x) = u(x) + v(x) . Тогда функция f получит прира-

щение

f = f (x + h) − f (x) = u(x + h) + v(x + h) − (u(x) + v(x)) = = u(x + h) − u(x) + v(x + h) − v(x) = u + v.

95

Следовательно

h→0	h	h→0	µ h			h ¶	′	′
lim	f	= lim		u	+	v	= u	(x) + v	(x).

Аналогично для разности функций.

2) Пусть g(x) = u(x)v(x) . Тогда функция g получит прираще-

ние

g= g(x + h) − g(x) = u(x + h) · v(x + h) − u(x)v(x) =

=u(x + h)v(x + h) − u(x)v(x + h) + u(x)v(x + h) − u(x)v(x) =

					= u · v(x + h) − u(x) · v.
Отсюда, так как функция v(x)					дифференцируема в точке x , зна-
чит, непрерывна в этой точке и					lim v(x + h) = v(x) , следует
					h→0
g′(x) = lim	g	= lim	u	lim v(x + h) + u(x) lim		v	=
	h		h
h→0		h→0		h→0	h→0	h

= u′(x)v(x) + u(x)v′(x) .

3) Пусть ϕ(x) = u(x)

v(x)

и v(x) =6 0 . Тогда O(x) x + h O(x)

v(x + h) 6= 0 и

ϕ =

u(x + h)

u(x)

−

=

v(x + h)

v(x)

=

u(x + h)v(x) − u(x)v(x) − u(x)v(x + h) + u(x)v(x)

=

v(x)v(x + h)

=

u · v(x) − u(x) · v

.

v(x)v(x + h)

Так как

v(x)

дифференцируема в точке

x , то она непрерывна в

этой точке, следовательно,

lim v(x + h) = v(x) , и

h→0

u

v

ϕ′(x) = lim

ϕ

= lim

h

v(x) − u(x) h

=

h

v(x) v(x + h)

= µh→0

h→0

−

h→0

h ¶

µh→0

h ¶ = u′(x)v(x) − u(x)v′(x) .

lim

u

v(x)

u(x)

lim

v

v(x) lim v(x + h)

v2(x)

h→0

96

Теорема о производной сложной функции. Пусть u(x) дифференцируема в точке x0 и u0 – ее значение в точке x0 . Пусть y = f (u) дифференцируема в точке u0 . Тогда сложная функция F (x) = f (u(x)) дифференцируема в точке x0 и имеет место формула F ′(x0) = f ′(u0) · u′(x0) .

Д о к а з а т е л ь с т в о. Функция f дифференцируема в точке u0 .

Следовательно приращение функции f	в точке u0		с шагом u = k
равно
kf (u0) = f ′(u0) · k + α(k) · k ,
где lim α(k) = 0 . Положим α(0) = 0 . Тогда α			C(0) и формула
k 0
→

kf (u0) = f ′(u0) · k + α(k) · k верна также и при k = 0 . Пусть

hu(x0) = u(x0 + h) − u(x0).

Рассмотрим

F (x0) = f (u(x0 + h)) − f (u(x0)) =

= f (u(x0) +

hu(x0)) − f (u(x0)) =

k=Δh u(x0)F (x0) =

= f ′(u0)Δhu(x0) + α (Δhu(x0))

hu(x0).

Тогда

F ′(x0) = lim

hF (x0)

=

h→0

h

hu(x0)

hu(x0)

= f ′(u

)

lim

+ lim α (Δ

u(x

)) lim

.

h

0

· h

→

0

h 0

h

0

h 0

h

→

→

Здесь функция u(x) дифференцируема в точке x0 , значит, u(x) непрерывна в точке x0 , и следовательно,

lim	lim (u(x	0	+ h)	−	u(x	)) = 0 ,
h 0	hu(x0) = h 0				0
→	→

но тогда и

lim α (Δhu(x0)) = α(0) = 0 ,

h→0

так как α C(0) . Поэтому

F ′(x0) = f ′(u0) · u′(x0) + 0 · u′(x0) = f ′(u0) u′(x0) .

Мы получили формулу

′

(f (u(x))) = f ′(u(x)) · u′(x) .

97

22.5.Инвариантность формы дифференциала первого порядка

В предыдущей теореме мы получили формулу для производной сложной функции yx′ = yu′ · u′x . Тогда для дифференциала

df (x0) = dy = yx′ dx = yu′ · u′x dx = yu′ · du = F ′(u0) du ,

и значит, dy = yu′ du . В других обозначениях, если y = y(x) , а x = ϕ(t) получим dy = yx′ dx . Но эта же формула верна для дифференциала функции, когда x – независимая переменная. Это и

значит, что имеет место свойство инвариантности формы первого дифференциала.

Заметим, что так как производная y′ = dxdy , то для производной сложной функции получается формула dxdy = dudy · dudx .

22.6. Дифференцируемость обратной функции

Теорема (дифференцируемость обратной функции).

Пусть функция y = y(x) определена, строго монотонно возрастает (убывает) и непрерывна в окрестности O(x0) точки x0 . Обозначим y0 = f (x0) . Тогда, если существует f ′(x0) 6= 0 , то

существует производная обратной функции ϕ′(y0) = 1 , т.е.

f ′(x0)

x′y = 1 .

yx′

Д о к а з а т е л ь с т в о. Дадим приращение			y , тогда x
– приращение обратной функции. Рассмотрим		x	(заметим, что
		y

y 6= 0 x 6= 0 – следствие строгой монотонности, y → 0 x → 0 – следствие непрерывности). Тогда по теореме о пределе

сложной функции

lim

x

=

lim

1

=

1

=

1

=

1

.

y

y

y

y

→

0

y

y

→

0

lim

lim

y′

x

y→0

x

x→0

x

x

Таким образом, x′y = 1 .

yx′

98

Лекция 21 (17.11.67)

§23. Производные элементарных функций

1) Если f (x) ≡ c ,

c = const , то

f ′(x) = lim

f (x + h) − f (x)

= lim

c − c

= 0 .

2)

h→0

h

h→0

h

h→0

h

−

= h→0

·

h

h ¡

h

¢

sin 2

=

(sin x) = lim

sin(x + h)

sin x

lim 2

· cos

x + 2

′

sin h

µ

h

¶

h→0

2

2

h→0

2

= lim

lim cos

x +

= cos x ,

h

так как cos x – непрерывная функция.

3)

′

π

′

π

¢

(cos x)

= cos

x +

·

1 =

−

sin x .

4)

=

¡sin ¡x + 2 ¢¢

¡

2

(tg x) = cos x · cos x − sin x · (− sin x)

=

1

,

cos x = 0 .

′

6

cos2 x

cos2 x

5)

′

1

(ctg x)

= −

,

sin x 6= 0 .

sin2 x

6)

f (x) = loga x ,

a > 0 , a 6= 1 . Имеем

f = loga(x + h) − loga(x) = loga µ1 + x ¶ .

h

то

¡

x

x

h→0

¢

– непрерывная функция и

Так как u(h) =

1 + h

h

lim u(h) = e ,

f

1

h

x loga

1 + hx

f ′(x) = h→0

log

a µ

¶

¡x

¢

=

h

h→0 h

x

h→0 h

lim

= lim

1 +

= lim

h→0 x loga µ

x

=

x h→0

a

x ln a .

x ¶

u(h) =

= lim

1

1 + h

h

1

lim log

1

99

7)

(ln x)′ =

1

.

x

8)

f (x) = ax ,

a > 0 , a 6= 1 . Имеем

f ′(x) = lim

ax+h − ax

= ax lim

ah − 1

.

h→0

h

h→0

h

Обозначим u(h) = ah

−

1 . Тогда ah

= 1 + u ,

h ln a = ln(1 + h) ,

h =

ln(1+h)

и

ln a

f ′(x) = ax lim

u

·

ln a = ax ln a .

h

0 ln(1 + u)

→

9)

f (x) = xa ,

x > 0 , a R . Так как

f (x) = xa = ea ln x , то

f ′

(x) = ea ln x ·

a

a

= axa−1 .

= xa

·

x

x

При a > 1

f ′(0) = lim

f (x) − f (0)

= lim

xa − 0

= lim xa−1 = 0 .

x→0

x

x→0

x

x→0

Если f (x) = x , то f ′(0) = lim

x−0 = 1 .

x→0+

x

10)

′

1

(arcsin x)

=

√

.

1 − x2

Функция y = arcsin x

– обратная к функции x = sin y при y из

h

i

отрезка

−π2 , π2

. По теореме о производной обратной функции

y′ =

1

=

1

=

1

=

1

,

1 < x < 1 .

11)

x′

cos y

+p1 − sin2 y

√1 − x2

−

′

1

(arccos x)

= −

√

.

1 − x2

Так как arccos x = π2 − arcsin x , то

′

′

1

(arccos x)

= − (arcsin x)

= −

√

,

−1 < x < 1 .

1 − x2

100