Лекции Стечкина по матану

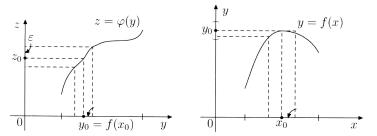
Рис. 4.7. Непрерывность сложной функции.

ϕ(y) определена для y L (L F (x) C(x0) .

f (M )) , ϕ(y) C(y0) . Тогда

Д о к а з а т е л ь с т в о. Из условий теоремы следует, что

ε > 0 δ > 0 y L , y f (M ) , |y − y0| < δ , |ϕ(y) − ϕ(y0)| < ε ,

δ > 0 η > 0 x M , |x − x0| < η , |f (x) − f (x0)| < δ .

Тогда для любого y		такого, что |y − y0| < δ ,			y f (M ) , имеем
y = f (x) и так как y0 = f (x0) , то
|ϕ(y) − ϕ(y0)| < ε , |ϕ(f (x)) − ϕ(f (x0))| < ε ,
т. е. |F (x) − F (x0)| < ε . Значит F (x) C(x0) .
Следствие. Пусть		F (x) = ϕ(f (x)) ,	lim f (x) = A ,			ϕ(y) опреде-
лена для y O(A) ,		x→x0
		ϕ(y) C(A) . Тогда			¶
x→x0		x→x0	ϕ µx→x0			,
lim	F (x) = lim ϕ(f (x)) =			lim f (x)
¯	¯	¯		½	A	(x = x0)
Д о к а з а т е л ь с т в о. Положим			f¯(x) =		f (x)	(x 6= x0) .
Тогда lim f (x)	= f (x0) , т. е. f (x) C(x0)			. Значит к этой функции
x x0
→

применима теорема о непрерывности сложной функции. Следова-

lim	¯		ϕ(f (x)) = ϕ lim	f (x)
	ϕ(f (x)) = ϕ(A) , откуда lim
тельно, x→x0		x→x0	µx→x0	¶
что доказывает утверждение.
Следствие.	lim f (x)	.
	lim ef (x) = ex→x0

x→x0

71

Лекция 15 (25.10.67)

§ 17. Функции, непрерывные на множестве

Пусть M X R и функция f (x) определена для x X . Говорят, что функция f (x) непрерывна на множестве M и обозначают f (x) C(M ) , если функция непрерывна в каждой точке

этого множества. Таким образом, f (x)		C(M ) , если x0	M
ε > 0 δ > 0	x X , |x − x0| < δ ,	|f (x) − f (x0)| < ε . Здесь
δ = δ (x0, ε) зависит и от x0 и от ε .
Рассмотрим сужение fM (x) функции		f (x) на множество	M :
fM (x) = f (x)	( x M ). Очевидно, что если f (x) C(M ) , то и

fM (x) C(M ) . При изучении функции на множестве будем считать, что M = X .

Пусть функция f (x) C(M ) . Нас интересует, какие свойства M

при переходе к образу при непрерывном отображении сохраняются, и какие не сохраняются.

При непрерывном отображении ограниченность не сохраняется.

Пример. M = (0, 1) , f (x) = x1 (x M ) , f (M ) = (1, ∞) .

При непрерывном отображении замкнутость не сохраняется.

Пример. M = (−∞, ∞) , f (x) = arctg x , f (M ) = ¡−π2 , π2 ¢ .

При непрерывном отображении открытое множество не обязано

переходить в открытое.

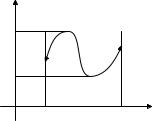
Пример. M = (0, 2π) , f (x) = sin x , f (M ) = [−1, 1] . Также для

функции, график которой изображен на рис. 4.8.

]
f (M )
[
a	M b

Рис. 4.8. Образ открытого множества не обязательно открытое множество.

72

§18. Свойства функций, непрерывных на множестве

18.1. Связность (линейная)

Определение. Множество M на числовой прямой связно (линейно связно), если оно обладает следующим свойством: если x, x′ M , то и [x, x′] M .

Замечание. Множество M на плоскости называется связным (линейно связным), если любые две точки x, x′ M могут быть соединены непрерывной линией, лежащей в этом множестве. Если M

открыто, в этом определении можно заменить непрерывную линию конечно-звенной ломаной (рис. 4.9).

x′ M

x

Рис. 4.9. Открытое связное множество на плоскости.

Теорема (структура связных множеств на числовой прямой). Связные множества – это отрезки, интервалы и полуинтервалы.

Д о к а з а т е л ь с т в о. Пусть M – связное множество на числовой прямой. Пусть α = inf x , β = sup x .

x M	x M
1). Пусть α > −∞ ,	β < +∞ (M ограничено). Тогда, если

α M , β M , то M = [α, β] , так как M – связное множество.

Если α M , β / M , то в этом случае γ , α < γ < β , x0 M γ < x0 < β . Тогда [α, x0] M , γ [α, x0] M , и, следовательно,

M – полуинтервал [α, β) .

2). α > −∞ , β = +∞ . Тогда M есть (α, ∞) или [α, ∞) . Аналогично для случая α = −∞ , β < +∞ .

73

3). α = −∞ , β = +∞ . Тогда M = (−∞, ∞) – вся числовая

прямая.

Сохранение связности. Пусть функция f (x) C(M ) , M R и

M – связно. Ниже мы докажем, что тогда f (M ) – связно.

Лемма об обращении непрерывной функции в нуль. Пусть f (x) определена на отрезке [a, b] и f (x) C [a, b] . Пусть также f (a)·f (b) < 0 . Тогда найдется такая точка c из интервала (a, b) ,

что f (c) = 0 .

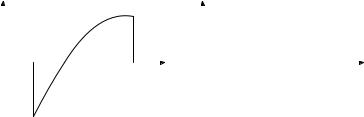
Замечание. Для несвязного множества лемма неверна (рис. 4.10).

y

y

a

0

c b1

b x

0

a

b

a′

b′

x

Рис. 4.10. Обращение непрерывной функции в нуль.

Д о к а з а т е л ь с т в о. Лемма доказывается методом деления пополам. Обозначим 0 = [a, b] . Разделим 0 пополам точкой b1 .

Возможны два случая:

1). f (b1) = 0 . В этом случае лемма доказана.

2). f (b1) =6 0 . Тогда f (b1) > 0 или f (b1) < 0 . Обозначим через 1 = [a1, b1] ту половину отрезка [a, b] , для которого выполняется

неравенство f (a1) · f (b1) < 0 . И так далее.

Тогда или процесс где-нибудь оборвется, и мы получим в одном из концов новых отрезков точку, где функция равна нулю; или мы

получим систему вложенных отрезков 0 1 ...							b na ... ,
для которых		n		·	n	, причем длины отрезков	2−	→
	f (a		)		f (b ) < 0		n		0

(n → ∞) . Допустим,
f (a) < 0 ,	f (b) > 0 ,
f (a1) < 0 ,	f (b1) > 0 ,

. . . . . . . . . . . . . . . . . . . . . . . . ..

74

f (an) < 0 , f (bn) > 0 ,

. . . . . . . . . . . . . . . . . . . . . . . . . . .

По теореме о стягивающейся системе отрезков существует единст-

венная точка c [an, bn] n . Тогда an → c ,		bn → c (n → ∞) , а
так как функция непрерывна, то
f (c) = nlim f (an) ≤ 0 ,	f (c) = nlim	f (bn) ≥ 0 .
→∞	→∞

Значит, f (c) = 0 .

Теперь легко может быть доказана следующая теорема.

Теорема о промежуточном значении. Пусть функция f (x)

определена и непрерывна на отрезке [a, b] и на его концах принимает разные значения: f (a) = A , f (b) = B , пусть A < B . Тогда для любого C такого, что A < C < B найдется точка ξ (a, b) такая, что f (ξ) = C .

Д о к а з а т е л ь с т в о. Введем функцию ϕ(x) = f (x) − C , тогда ϕ(x) непрерывна на [a, b] и принимает на концах этого отрезка значения разных знаков: ϕ(a) = A − C < 0 , ϕ(b) = B − C > 0 . По лемме об обращении непрерывной функции в нуль ξ (a, b)

ϕ(ξ) = 0 . Так как ϕ(ξ) = f (ξ) − C , то f (ξ) − C = 0 и f (ξ) = C .

Теорема. Пусть M – связное множество, f (x) C(M ) . Тогда и f (M ) связно.

Д о к а з а т е л ь с т в о. Обозначим Y = f (M ) . Пусть точки A и B принадлежат Y и для определенности A < B . Покажем, что [A, B] Y . Именно докажем, что если C – любая точка такая, что

A < C < B , то C Y .

Так как значения A, B Y , то a, b M f (a) = A , f (b) = B . В силу связности множества M отрезок [a, b] M . Функция f (x) непрерывна на отрезке [a, b] , следовательно, по теореме о промежуточном значении, ξ [a, b] , ξ M , f (ξ) = C . Таким образом, любая промежуточная точка C между A и B имеет прообраз. Значит, весь отрезок [A, B] лежит в Y и множество f (M ) связно.

Вопросы к коллоквиуму.

1.Счетность множества рациональных чисел.

2.Верхняя и нижняя грани числового множества.

3.Лемма о стягивающихся отрезках.

75

4. Лемма о выделении конечного покрытия.

5. Свойства функции (последовательности), имеющей предел (ограниченность, сохранение знака, единственность предела).

6. Свойства бесконечно малых. Предел суммы, произведения, частного.

7. Переход к пределу в неравенствах. lim sin x = 1 .

x→0 x

8.Теорема о пределе монотонной функции. Число e.

9.Теорема об эквивалентности двух определений предела.

10.Теорема о существовании предельной точки. Критерий Коши для последовательности. Критерий Коши для функций.

11.Сравнение бесконечно малых.

Лекция 16 (27.10.67)

18.2. Непрерывный образ отрезка

Лемма Больцано – Вейерштрасса. Пусть имеется последова-

тельность {xn} (n N) и |xn| ≤ K n N . Тогда существует последовательность натуральных чисел {nk} , nk ↑↑ , такая, что

подпоследовательность {xnk } сходится.

Таким образом, из всякой ограниченной последовательности можно выбрать сходящуюся подпоследовательность.

Д о к а з а т е л ь с т в о л е м м ы. Последовательность {xn}

ограничена, следовательно, по лемме Больцано –Вейерштрасса для бесконечных ограниченных точечных множеств (п. 13.2) для {xn} существует хотя бы одно предельное значение a . Построим подпоследовательность {xnk } , сходящуюся к a. Выберем εk > 0 , εk ↓ 0 (k → ∞) . Тогда

для	ε1	n1	|a − xn1 | < ε1 ;
для	ε2	n2 ,	n2 > n1 , |a − xn2 | < ε2 ;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
для	εk nk ,		nk > nk−1 , |a − xnk | < εk ;
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Теперь для подпоследовательности				{xnk } ε > 0 k0	k ≥ k0
εk < ε и |a − xnk | < εk < ε . Значит				xnk → a (k → ∞) .

Теорема об ограниченности непрерывной функции. Пусть функция y = f (x) определена и непрерывна на отрезке [a, b] . То-

76

гда функция f (x) ограничена на этом отрезке, т. е. найдется K такое, что x [a, b] |f (x)| ≤ K .

Д о к а з а т е л ь с т в о от противного. Предположим, что утверждение леммы неверно. Пусть, для определенности, функция f (x) не является ограниченной сверху. Тогда K > 0 x0 [a, b] f (x0) > K .

Зададим последовательность Kn > 0 , Kn ↑ ∞ (n → ∞) . Тогда
xn [a, b]	f (xn) > Kn . По лемме Больцано – Вейерштрасса
{xnk } xnk	→ c [a, b] (k → ∞) . Тогда f (xnk ) > Knk , т. е.
f (xnk ) → ∞ (k → ∞) .		f (x) C(c) . Следова-
С другой стороны, f (x) C [a, b] , значит,
тельно, f (xnk ) → f (c) (k → ∞) , так как		xnk → c (k → ∞) . Мы
пришли к противоречию.

Теорема о достижимости верхней и нижней граней. Всякая непрерывная функция на отрезке имеет максимум и минимум. Д о к а з а т е л ь с т в о. Пусть f (x) C [a, b] . По теореме об ограниченности непрерывной на отрезке функции f (x) на этом

отрезке ограничена. Значит она имеет конечные верхнюю грань

sup f (x) = M и нижнюю грань	inf = m , m		≤	M . Докажем,
x [a,b]	x	[a,b]

что значения M и m и есть максимальное и минимальное значения функции на отрезке [a, b] .

Допустим противное. Пусть x [a, b]			f (x) < M . Тогда функция
	(x) > 0 (x			[a, b]) . Значит, положи-
M − f (x) C [a, b] и M − f1
тельная функция ϕ(x) =		тоже есть функция, непрерывная

M −f (x)

на всем отрезке [a, b] . По теореме об ограниченности непрерыв-

ной на отрезке функции ϕ(x)		ограничена. Значит								K > 0 K,
				1		≤ K ,	1
K > 0 , ϕ(x) ≤ K x [a, b] . Тогда									≤ M − f (x)
			M	−	f (x)		K
1
x [a, b] , т. е. f (x) ≤ M −		< M	x [a, b] . Это противоре-
	K

чит тому, что M – верхняя грань функции. Значит, верхняя грань функции достигается и x0 [a, b] f (x0) = M .

Аналогично, нижняя грань непрерывной на отрезке функции достигается, т. е. x1 [a, b] f (x1) = m .

Теорема (свойство Дарбу, Д-свойство). Непрерывный образ отрезка есть отрезок.

Д о к а з а т е л ь с в о. Пусть функция f (x) определена на отрезке

77

[a, b] , f (x) C [a, b] . Тогда x0 [a, b]						f (x0) = M =		sup f (x) , и
								x [a,b]
	x		[a, b]	inf	f (x) . Значит, M, m			f ([a, b]) . Так
		1		f (x1) = m = x [a,b]
как			f ([a, b])	– связное множество, то [m, M ] f ([a, b]) . Следова-
тельно, f ([a, b]) = [m, M ] .
		Заметим, что свойство Дарбу переводить отрезок в отрезок есть
необходимое, но не достаточное для непрерывности функции.
Пример. Рассмотрим функцию f (x)						= sin 1 на полуинтервале
(0, 1] и f (0) = 0 (рис. 4.11).						x
		1) Если возьмем [a, b] , a > 0 , [a, b] (0, 1) , то f (x) C [a, b] и
по теореме образ отрезка [a, b]					есть отрезок.
		2) Если возьмем [0, b] , то			f ([0, b])	= [−1, 1] , но функция не

является непрерывной на [0, b] .

y

0	] [	]		x
	a	b	1

Рис. 4.11. Функция sin 1	на полуинтервале (0, 1] .
x

18.3. Непрерывность обратной функции

Определение. Функция f (x) на множестве M называется строго монотонной, если она строго возрастает ( f (x) ↑↑ ), или строго убывает ( f (x) ↓↓ ) на множестве M .

Функция f (x) строго возрастает (строго убывает) на множестве M , если для любых x, x′ M , x < x′ , выполняется f (x) < f (x′)

( f (x) > f (x′) ).

78

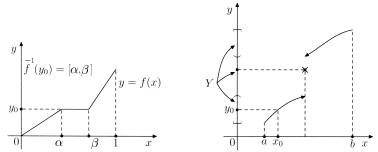
Пусть для функции f (x) существует обратное отображение. Если обратное отображение однозначно, то назовем его обратной функцией (рис. 4.12).

Рис. 4.12. Обратное отображение. Для строго монотонной функции обратное отображение однозначно.

Лемма о существовании обратной функции. Пусть функция f (x) определена и f (x) ↑↑ на множестве M R . Обозначим через Y = f (M ) образ множества M . Тогда на множестве Y

−1

существует обратная функция f (y) = ϕ(y) (y Y ) .

Таким образом, для строго монотонной функции обратное отображение однозначно (рис. 4.12).

Д о к а з а т е л ь с т в о. Если y0 Y , то x0 M f (x0) = y0 ,

−1	−1
x0 f (y0) . Надо доказать, что	f (y0) = x0 , т. е. других точек в
−1
f (y0) нет. Пусть x < x0 , тогда	f (x) < f (x0) = y0	и значит x не
меньше x0 . Пусть x > x0 , тогда f (x) > f (x0) = y0		и значит x не
	−1

больше x0 . Следовательно, x = x0 и f (y0) = x0 .

Лемма о монотонности обратной функции. Если функция

f (x) определена и f (x) ↑↑ или	f (x) ↓↓ на		M, то и обратная
функция ϕ(y) ↑↑ или ϕ(y) ↓↓ на	Y = f (M ) .		y, y′	Y , y < y′ .
Д о к а з а т е л ь с т в о. Пусть		f (x) ↑↑ ,
Докажем, что ϕ(y) < ϕ(y′) . Пусть		x = ϕ(y) , x′		= ϕ(y′) . Тогда

x < x′ , так как если бы было x > x′ , то f (x) > f (x′) , т. е. y > y′

и мы получили противоречие. Аналогично рассматривается случай f (x) ↓↓ .

79

Лекция 17 (01.11.67)

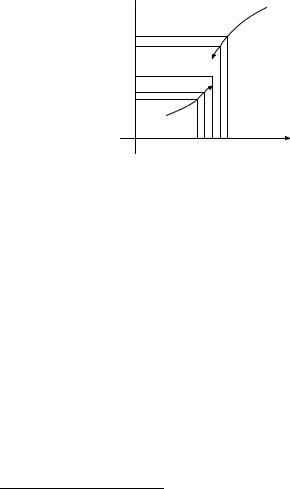
Лемма о непрерывности обратной функции. Пусть функция y = f (x) ↑↑ на [a, b] . Пусть Y – область значений этой функции и x = ϕ(y) (y Y ) – обратная функция. Тогда ϕ(y) C(Y ) 2) .

y

y

0	a	(	)	b x
		x0	x x1

Рис. 4.13. Лемма о непрерывности обратной функции.

Д о к а з а т е л ь с т в о. Пусть x – произвольная точка из [a, b] . Зададим ε > 0 и построим O(x) радиуса ε . Обозначим x0 = x − ε , x1 = x + ε (рис. 4.13). (Здесь используется, что M – отрезок!) Если x – внутренняя точка, то пусть x0, x1 [a, b] . Рассмотрим

y0 = f (x0) < y = f (x) < y1 = f (x1) . Построим δ > 0 (δ = δ(ε))

такое, что Oδ (y) (y0, y1) . По условию монотонности обратной функции y′ Oδ (y) ϕ(y) − ε < ϕ(y′) < ϕ(y) + ε , т. е. выполняется неравенство |ϕ(y′) − ϕ(y)| < ε . Значит, обратная функция непрерывна в точке y.

Если x = a или x = b , то достаточно рассмотреть односторонние интервалы.

Пример. На рис. 4.14 изображена функция, непрерывная и монотонная на [a, b) S [c, d] , для которой обратная функция разрывна.

Из доказанных лемм следует следующая теорема.

Теорема о существовании, монотонности и непрерывности обратной функции. Пусть функция f (x) ↑↑ и непрерывна

2) "Суть вся в том, что M – отрезок, т. е. исключаются какие-то там "уроды"." (С. Б. С.)

80