Лекции Стечкина по матану

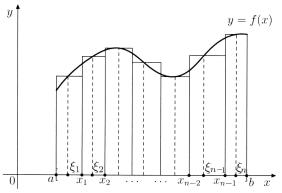
F (t) при t → 0 , если ε > 0 δ > 0 t , 0 < t < δ , y F (t) |A − y| < ε .

Геометрическую интерпретацию, поясняющую определение, смо-

три на рис. 9.1.

Определение интеграла Римана. Пусть на отрезке [a, b] задана функция y = f (x) . Рассмотрим систему точек (рис. 9.2)

a = x0 < x1 < ... < xk < ... < xn = b .

Будем говорить, что такая система определяет разбиение T отрезка [a, b] . Определим диаметр разбиения – это число

t = d(T ) = max xk > 0 ,

k=1,...,n

где xk = xk −xk−1 . В каждом из отрезков [xk−1, xk] , где k принимает значения 1, 2, ..., n , зафиксируем точку ξk . Мы получим n

точек ξ1, ξ2, ..., ξn . Вектор (ξ1, ξ2, ..., ξn) обозначим через ξ . При заданном T и векторе ξ строим интегральную сумму Римана

n	n
X	X
S(T, ξ) = f (ξk)(xk − xk−1) =	f (ξk) xk .
k=1	k=1

Рис. 9.2. Интегральная сумма Римана.

Каждое разбиение T имеет свой диаметр d(T ) = t > 0 . Поставим каждому t в соответствие множество всех таких интегральных

161

сумм S(t) = S(T, ξ) при различных разбиениях T, что d(T ) = t , при различных векторах ξ . Интегралом Римана называется число I , являющееся пределом интегральных сумм

I = lim S(t) ,

t→0

если этот предел существует. Обозначается интеграл Римана

	b			b
I = Za		f (x)dx = (R) Za		f (x)dx .
				2 семестр
				Лекция 3
				(21.02.68)
Если для функции f (x)		существует интеграл Римана на отрезке
[a, b] , то говорят, что	f (x)		интегрируема по Риману на отрезке
[a, b] . Если функция	f (x)		интегрируема по Риману, то мы будем

говорить, что f R [a, b] , где R [a, b] – множество функций, инте-

грируемых по Риману.

Интеграл – один из простейших функционалов, определенных на классе R [a, b] .

Рассмотрим, как понятие интеграла связано с характеристикой точечного множества на отрезке.

Пусть на отрезке [a, b] задано точечное множество E R и χ – характеристическая функция множества E , т. е. функция

½	0,	если	x [a, b] \E.
χ(x) = χE (x) =	1,	если	x E,

Если χ(x) R [a, b] , то будем говорить, что множество E имеет

b

R

длину, равную χ(x)dx = I(χ) = F (E) . Если χ(x) / R [a, b] , то

a

будем говорить, что E не имеет длины.

Замечание. Геометрически интеграл Римана от неотрицательной функции на отрезке [a, b] – это площадь криволинейной трапеции, образованной графиком функции, отрезком [a, b] и прямыми x = a и x = b .

Определение интеграла можно дать и на "языке ε – δ ".

162

Определение. Число I называется интегралом I =	b
	f (x)dx от
	a
функции f (x) на отрезке [a, b] , если для любого ε > 0	Rсуществует

такое δ > 0 , что для всех разбиений T отрезка [a, b] с диаметром d(T ) , меньшим, чем δ , и для всех промежуточных точек ξ выполняется неравенство |S(T, ξ) − I| < ε .

Числа a и b называются нижним и верхним пределами интегри-

рования соответственно.

b

R

Отметим, что I = f (x)dx = F (f, a, b) не зависит от x , x

– связанная переменная,a в отличие от неопределенного интеграла

R

f (x)dx = F (x) + C , зависящего от x .

Выясним, какие функции интегрируемы по Риману, т. е. из каких функций состоит класс R [a, b] .

§ 38. Функции, интегрируемые по Риману

Теорема (необходимое условие интегрируемости функции).

Для того, чтобы функция была интегрируема по Риману на отрезке [a, b] необходимо, чтобы она была ограничена на этом отрезке.

Д о к а з а т е л ь с т в о от противного. Пусть функция f (x) интегрируема на отрезке [a, b] и не является на нем ограниченной. Это значит, что для любого разбиения T найдется такой частичный отрезок разбиения [xk−1, xk] , что функция останется неограниченной на этом отрезке, т. е. sup |f (x)| = ∞ .

[xk−1,xk ]

Возьмем произвольное разбиение T отрезка [a, b] . Найдем такой отрезок [xk−1, xk] этого разбиения, на котором функция неограничена. Построим вектор ξ = (ξ1, ξ2, ..., ξn) . Точки

ξ1, ξ2, ..., ξk−1, ξk+1, ..., ξn

зададим произвольно ( ξi [xi−1, xi] ). Тогда, если зафиксировать T и точки ξi ( i =6 k ), интегральная сумма S(T, ξ) для функции f (x) останется зависимой только от ξk . Запишем интегральную

163

сумму в виде

	n
	X
S(ξk) =	f (ξi)Δ xi + f (ξk)Δ xk .
	i=1, i6=k,

Первое слагаемое правой части зафиксировано; xk также зафиксировано вместе с разбиением T . Точка ξk принадлежит отрезку [xk−1, xk] , на котором функция неограничена, значит, f (ξk) тоже неограниченная функция. Тогда и S(ξk) есть неограниченная

функция, т. е.

sup |S(ξk)| = ∞ .

ξk [xk−1,xk ]

Но тогда и sup |S(T, ξ)| = ∞ для любого разбиения T . Отсюда сле-

ξ

дует, что не существует предела интегральных сумм S(T, ξ) , что

противоречит тому, что функция интегрируема по условию теоремы.

Рассмотрим критерии и достаточные условия интегрируемости

функции, т. е. существования предела I = lim S(T, ξ) . Согласно

t→0

критерию Коши существование этого предела означает, что интегральные суммы S(T, ξ) и S(T ′, ξ′) должны быть близки друг другу, если диаметры разбиений d(T ) и d(T ′) достаточно малы.

Для дальнейшего нам понадобится исследовать при фиксированном разбиении T величину

sup S(T, ξ)	−	S(T, ξ′)	= sup S(T, ξ)	−	inf S(T, ξ′) .
ξ,ξ′ |		|	ξ		ξ′
Величина sup S(T, ξ)		называется верхней суммой Дарбу и обо-
ξ

значается S(T ) . Величина inf S(T, ξ) называется нижней суммой

ξ

Дарбу и обозначается S(T ) .

Найдем более простые выражения для верхней и нижней сумм

Дарбу. Пусть функция	f (x) ограничена на отрезке [a, b] . Тогда
найдется M такое, что для всех x [a, b]		справедливо |f (x)| ≤ M .
Зафиксируем разбиение T и отрезок [xk−1, xk] . Пусть
Mk = sup	f (x) , mk =	inf	f (x) .
x [xk−1,xk ]		x [xk−1,xk ]
164

Теорема (формулы Дарбу). Пусть функция f (x) ограничена на отрезке [a, b] , T – разбиение отрезка [a, b] ,

Mk = sup			f (x); mk =		inf	f (x) .
		x [xk−1,xk ]		x [xk−1,xk ]
Тогда
		n			n
		X			X
	S(T ) =		Mk	xk, S(T ) =	mk	xk .
		k=1			k=1
Д о к а з а т е л ь с т в о. Имеем
			n	n
			X	X
		S(T, ξ) =		f (ξk)Δ xk ≤ Mk		xk .
			k=1	k=1

Эта оценка верна для любого выбора точек ξk . Значит

n

X

sup S(T, ξ) ≤ Mk xk ,

ξk=1

откуда

n

X

Mk

xk .

S(T ) ≤

k=1

Зададим произвольное ε

> 0 . Подберем точки ξk [xk−1, xk]

( k = 1, 2, ..., n ) так, что

f (ξk) > Mk − ε . Тогда для этого набо-

ра ξ

n

n

X

X

Mk xk − ε(b − a),

S(T, ξ) =

f (ξk)Δ xk >

k=1

k=1

n

xk = b − a

так как сумма

равна длине отрезка [a, b] . Следо-

вательно,

k=1

P

n

X

S(T ) = sup S(T, ξ) ≥ Mk xk

ξk=1

			n
			P	xk .	n
	и значит, S(T ) = Mk
			k=1		P
	Аналогично доказывается формула S(T ) =
					mk xk .

k=1

165

Замечание. Обозначим Mk − mk = ωk = ωk(f, xk−1, xk) – колебание функции f (x) на отрезке [xk−1, xk] . Тогда

sup S(T, ξ)	−	S(T, ξ′)			|	= sup S(T, ξ)		−	inf S(T, ξ′) =
ξ,ξ′ |						ξ			ξ′
						n				n
						X				X
							(Mk − mk)Δ xk =			ωk	xk .
	= S(T ) − S(T ) =
						k=1				k=1
Определение. Пусть есть два разбиения T и T1 отрезка											[a, b] .
Говорят, что	T1		– продолжение разбиения T (будем записывать
T1 T ), если всякая точка деления, входящая в T, входит и в T1 .
Пусть функция f (x)						ограничена на отрезке [a, b] . Рассмотрим
простейшие свойства сумм Дарбу.

Свойство 1. Если T1 T , то S(T1) ≤ S(T ) и S(T1) ≥ S(T ) .

Д о к а з а т е л ь с т в о. Достаточно ограничиться присоединением к уже имеющимся точкам разбиения еще одной точки x′ . Пусть эта точка попадет между точками xk−1 и xk , так что xk−1 < x′ < xk . В сумме S(T ) этому отрезку отвечало слагаемое Mk xk , а в сумме S(T1) – сумма двух слагаемых Mk′ (x′ − xk−1) + Mk′′(xk −x′) , где

Mk′ и Mk′′

– верхние грани функции f (x)

на отрезках [xk−1, x′] и

[x′, xk]

соответственно. Так как эти отрезки являются частями от-

резка

[xk−1, xk] , то Mk′

≤ Mk , Mk′′

≤ Mk и значит, имеют место

M ′

(x′

−

x

k−1

)

≤

M

k

(x′

−

x

k−1

) и M ′′(x

x′)

≤

M

k

(x

x′) . Скла-

k

k

k −

k −

дывая эти неравенства почленно, получим

Mk′ (x′ − xk−1) + Mk′′(xk − x′) ≤ Mk

xk .

Отсюда и следует, что S(T1) ≤ S(T ) .

Аналогично для нижней суммы S(T1) ≥ S(T ) .

Свойство 2. Для любых двух разбиений T

и

T ′

нижняя ин-

тегральная сумма не превосходит верхней интегральной суммы:

S(T ) ≤ S(T ′) .

Д о к а з а т е л ь с т в о. Для доказательства построим разбиение T1 = {T, T ′} , которое содержит все точки разбиений T и T ′ . Тогда

T1 T , T1 T ′ , откуда S(T1) ≤ S(T ′) и S(T ) ≤ S(T1) . Но по определению S(T1) ≤ S(T1) , а отсюда S(T ) ≤ S(T ′) .

Из этого свойства вытекает, что по всем разбиениям T

sup S(T ) ≤ inf S(T ) .

TT

166

		n
Обозначим Ω(T ) =		ωk xk .
		k=1
Теорема	(предельный критерий интегрируемости функ-
		P

ций). Для того, чтобы на отрезке [a, b] функция f (x) была интегрируема по Риману, необходимо и достаточно, чтобы выпол-

нялось условие lim Ω(T ) = 0 .

d(T )→0

2 семестр Лекция 4 (23.02.68)

Д о к а з а т е л ь с т в о теоремы. Н е о б х о д и м о с т ь. Пусть функция f R [a, b] , т. е. существует предел интегральных сумм

lim S(T, ξ) = I . Зададим произвольное ε > 0 . В силу того, что

t→0

lim S(T, ξ) = I , δ > 0 T , d(T ) < δ , ξ |S(T, ξ) − I| < ε . От-

t→0

сюда, при тех же условиях, S(T, ξ) < I + ε . Значит, T , d(T ) < δ ,

S(T ) ≤ I + ε .

Аналогично доказывается, что S(T ) ≥ I − ε .
	Таким образом, ε > 0	δ > 0 T , d(T ) < δ , S(T )−S(T ) ≤ 2ε
и	0 ≤ Ω(t) ≤ 2ε . Это значит, что t			0
			lim Ω(T ) = 0 .
Д о с т а т о ч н о с т ь. Пусть			→
	t→0	т. е.	t→0	©			−	S(T )	ª
	lim Ω(T ) = 0,		lim	S(T )					= 0 .

Надо доказать, что существует предел интегральных сумм Римана. По свойствам сумм Дарбу S(T ) ≤ S(T ′) для любых разбиений T

и T ′ . По теореме отделимости I

T и T ′ S(T ) ≤ I ≤

S

(T ′) .

Докажем, что

I = lim S(T, ξ) . Зададим ε > 0 . В силу того, что

t→0

lim Ω(T ) = 0 для этого

ε

δ > 0

T

, d(T ) < δ , S(T ) −S(T ) < ε .

t 0

→

и по определению интегральной суммы

Имеем S(T ) ≤ I ≤ S(T )

S(T ) ≤ S(T, ξ) ≤ S(T ) .

Отсюда получаем, что S(T, ξ) ≤ S(T ) ≤ S(T ) + ε ≤ I + ε . Аналогично S(T, ξ) ≥ I − ε .

Это значит, что |S(T, ξ) − I| ≤ ε для любого выбора ξ , если только

d(T ) < δ . Следовательно, существует lim S(T, ξ) = I .

t→0

167

Теорема (критерий Дарбу). Для того, чтобы функция была интегрируема на отрезке [a, b] , необходимо и достаточно, чтобы

inf Ω (T ) = 0 .

T

Д о к а з а т е л ь с т в о. Н е о б х о д и м о с т ь очевидна, так как данный критерий содержит более слабое требование, чем предельный критерий интегрируемости.

Д о с т а т о ч н о с т ь. Пусть дано, что inf Ω (T ) = 0 , тогда

ε > 0

. Докажем, что

T

.

T Ω (T )

< ε

lim Ω (T ) = 0

t→0

Выберем произвольное

ε > 0 . Пусть

T0

– такое фиксированное

разбиение отрезка [a, b] , что

Ω (T0) < ε . Докажем, что

δ > 0

T , d(T ) < δ , Ω (T ) < 2ε .

n0

ωk0

xk0 . Таким образом, у нас за-

По определению Ω (T0) =

ε

k=1

T

, а вместе с

T

число n

и

разбиение

фиксированы число

и

P

0

0

0

точки x0 . Отметим, что если

T ′

T , то

Ω (T ′)

≤

Ω (T ) . Пусть

k

0

δ0 = min

xk

> 0 – длина наименьшего из отрезков разбиения T0 .

k

Пусть далее

δ < δ0 . Рассмотрим произвольное разбиение

T , для

которого d(T ) < δ . В каждом отрезке этого разбиения T окажется не более одной точки разбиения T0 .

Построим разбиение T ′ , состоящее из всех точек разбиений T0 и T . Тогда T ′ T0 , T ′ T и Ω (T ′) ≤ Ω (T0) < ε .

Рассмотрим те отрезки разбиения T , которые содержат точки T0 . Их всего n0 + 1 . Длина каждого такого отрезка не более d(T ) = t . Значит, сумма длин всех этих отрезков σ ≤ t(n0 + 1) .

Разобьем Ω(T ) на два слагаемых:

n

X

Ω (T ) = ωk xk = Σ1 + Σ2,

k=1

где сумма Σ2 распространена на выделенные отрезки, а сумма Σ1

– на оставшиеся отрезки.

	– часть суммы Ω(T ′) , т. е. все члены суммы			n
Σ1				ωk xk ,
входящие в Σ1 , входят и в Ω(T ′) , откуда			1 Ω(T ′)	k=1
		Σ		P
			≤	< ε .
Σ2	содержит отрезки общей длины σ .

Если ωk – верхняя грань колебания функции на маленьком отрезке длины xk , то ωk ≤ ωf , где ωf – верхняя грань колебания функ-

168

ции на всем отрезке [a, b] . Значит,

X X

ωk xk ≤ ωf xk ≤ tωf (n0 + 1) .

2 2

Таким образом, Ω (T ) ≤ ε + tωf (n0 + 1) . Здесь			ε ,		ωf , n0 + 1 от
функции f (x) . Значит, если δ1 = min	δ0,	ε		o	, то Ω (T ) < 2ε
		ωf (n0+1)
для всех t < δ1 . Следовательно, lim	n
Ω (T ) = 0 .

t→0

Теорема (критерий Римана). Для того, чтобы ограниченная функция f (x) была интегрируема на отрезке [a, b] , необходимо и достаточно, чтобы для любого ε > 0 и для любого η > 0 существовало такое разбиение T отрезка [a, b] , что

		X
		xk < η ,
	P≥	k,ωk ≥ε
		xk – сумма xk по таким k , для которых ωk ≥ ε .
	где
	k,ωk	ε

Д о к а з а т е л ь с т в о. Н е о б х о д и м о с т ь. Предположим

противное, т. е. пусть		ε0 > 0	η0	> 0 T		xk ≥ η0 .
					k,ωk	ε
Тогда для любого разбиения T					P≥
	X	X		xk ≥
Ω (T ) =	ωk xk +		ωk
	k,ωk <ε0	k, ωk ≥ε0		X
	≥	X			xk ≥ ε0η0 > 0 .
		ωk	xk ≥ ε0
		k, ωk ≥ε0		k, ωk ≥ε0

Отсюда следует, что inf Ω (T ) > 0 и по критерию Дарбу функция

T

f (x) не является интегрируемой, что противоречит условию. Необ-

ходимость доказана.

Д о с т а т о ч н о с т ь. Пусть для функции ω = ω [a, b] 6= 0 (ина-

че функция постоянная и значит, интегрируемая). Зададим произ-

	вольно	ε	> 0 . Тогда для η =	ε	по условию теоремы найдется
		b−a		ω
					169

P

ε

такое разбиение T, что

ε

xk <

ω

и значит,

k, ωk ≥

b−a

X

X

Ω(T ) = k, ωk <

ε

ωk

xk + k, ωk ≥

ε

ωk

xk ≤

b−a

b−a

X

≤

ε

X

xk + ω

xk ≤

b a

ε

ε

−

k, ωk

≥

k, ωk < b−a

b−a

≤

ε

(b − a) + ω

ε

= 2ε .

b − a

ω

Итак, Ω (T ) ≤ 2ε , т. е. неотрицательную величину Ω (T ) можно

сделать меньше любого наперед заданного положительного числа

2ε . Тогда inf Ω (T ) = 0 и функция интегрируема по критерию Дар-

T

бу.
Определение. Пусть ограниченная функция							f (x)		задана на от-
резке [a, b] и пусть x0 (a, b) . Рассмотрим отрезок									[α, β] , содер-
жащий точку	x0 строго внутри себя. Пусть ω [α, β] – колебание
функции f (x)	на отрезке [α, β]
	ω [α, β] = sup		f (x) − x	inf		f (x)	≥	0 .
					[α,β]
		x [α,β]
Очевидно, что если		[α′, β′]	[α, β] , то			ω [α′, β′] ≤ ω [α, β] . При
стягивании точек αn		и βn	к точке	x0		получим монотонно убы-

вающую последовательность колебаний {ω [αn, βn]} , которая име-

ет предел при αn → x0 , βn → x0		( n → ∞ ). Этот предел на-
зывается колебанием функции f (x)		в точке x0 и обозначается
ωf (x0) = lim	ω [αn, βn] . Колебания функции в точках a и b опре-
n→∞	ωf (a) = nlim ω [a, βn] , где βn → x0 ( n → ∞ ), и
деляются как
	→∞

ωf (b) = lim ω [αn, b] , где αn → x0 ( n → ∞ ).

n→∞

Заметим, что

1)	ωf (x0) не зависит от выбора последовательности {[αn, βn]} ;
2)	ωf (x0) = 0	функция f (x) непрерывна в точке x0 ;
3)	ωf (x0) > 0	в точке разрыва.

170