Глава 6. Построение статистических регрессионных моделей

6.1. Основные положения

Многофакторный регрессионный анализ служит для отыскания количественной зависимости между результирующим показателем (откликом) Y и независимыми факторами, (переменными) Х = {}, которые оказывают влияние на Y. Требуется установить зависимость отклика Y от факторов X, число которых k, т.е. у = f{}.

Значения отклика и фактора определяются в ходе пассивного или активного эксперимента над объектом. Количество факторов должно быть заранее установлено, т.е. значения известны. Сам вид функции связи факторов и откликов заранее неизвестен и должен быть установлен в ходе анализа. Кроме того, задача анализа состоит в определении численных параметров, входящих в эту функцию. Необходимо учитывать, что кроме установленных факторов на отклик y влияют случайные величины, значения которых в ходе эксперимента не определяются.

Таким образом, можно говорить о математическом ожидании отклика y, который связан с факторами уравнением регрессии

(6.1)

Описательные возможности линейного уравнения регрессии достаточно низки, поэтому для повышения адекватности модели в нее добавляют нелинейные зависимости. Например, парное взаимодействие факторов. Кроме того, нелинейные члены уравнения можно записать в виде квадратов, кубов и т.д.

В общем виде уравнение можно представить следующим образом:

(6.2)

Следует учитывать, что по конечной выборке, полученной в результате наблюдений, мы имеем не сами коэффициенты, а их оценки. В результате подстановки их в уравнение регрессии будет получена оценка математического ожидания. Ее запись аналогична записи предыдущего уравнения.

Пусть имеется n результатов наблюдений над величиной у, зависящей от k факторов, причем степень полинома равна d. Тогда число коэффициентов регрессии равно C и определяется как число сочетаний

.

Для получения возможности вычисления этих коэффициентов необходимо, чтобы количество опытов превышало .

Для проведения регрессионного анализа следует соблюдать следующие условия:

• случайная величина у должна иметь нормальное распределение;

• независимые переменные фактора X должны измеряться с погрешностью, пренебрежимо малой по сравнению с дисперсией случайной величины у.

Уравнение регрессии можно упростить, если ввести следующие обозначения:

1)  фиктивная переменная при свободном члене;

2) произведения двух переменных можно заменить, обозначив их следующим образом:

(6.3)

конечное значение, соответствующее общему количеству переменных, включенных в уравнение регрессии. Его максимальное значение определяется следующим образом:

.

Таким образом, оценка математического ожидания наблюдаемой величины определяется формулой

.

(6.4)

Здесь  оценка коэффициента. Штрих в дальнейшем можно опустить.

6.2. Матричный метод построения уравнения регрессии

Используем метод наименьших квадратов для определения коэффициентов регрессии по результатам наблюдений. Составим следующую систему линейных уравнений:

(6.5)

Значения результатов 1-го опыта имеют индекс 1, k-го  k.

Результаты этих наблюдений можно записать в матричной форме, где Х  матрица значений независимых переменных.

.

(6.6)

Коэффициенты регрессии можно представить в виде вектора В, а наблюдаемые значения переменной  в виде соответствующего вектора Y:

, .

(6.7)

Тогда систему можно записать в виде

Х  В = Y.

(6.8)

Для нахождения оценок по методу наименьших квадратов необходимо выяснить, при каких значениях коэффициентов В достигается минимум выражения

.

(6.9)

Приравняв к нулю частные производные выражения (6.9) по b_i, получим систему уравнений относительно неизвестных коэффициентов b_i:

(6.10)

Решением этой системы и будут оценки искомых коэффициентов b_i.

Представив результаты наблюдения в матричной форме в соответствии с формулами (6.6)  (6.7), можно осуществить решение системы линейных уравнений (6.5), вычислив произведение (6.8) в определенной последовательности.

Обе части уравнения (6.8) умножим на транспонированную матрицу :

.

(6.11)

Если в матрице ||x_ij|| переставлены местами строки и столбцы, то полученная матрица ||x_ji|| называется транспонированной к ней и обозначается как .

Обозначим C= X.

Вычислив определитель и матрицу алгебраических дополнений, определим обратную матрицу:

.

(6.12)

Здесь a_ij – алгебраические дополнения к элементам c_ij;  определитель матрицы.

Окончательно расчетное выражение для вычисления коэффициентов регрессии имеет вид

B = C ^-1 Y.

(6.13)

После определения коэффициентов регрессии необходимо установить правильность выбора регрессионной модели, т.е. проверить адекватность полученного уравнения регрессии. Такая проверка позволяет установить правомерность ограничения полинома регрессии выбранной степенью d. Например, сначала необходимо использовать линейное уравнение регрессии, затем уравнение 2-й степени и т.д.

Проверка адекватности осуществляется путем сопоставления расчетного значения критерия Фишера с критическим. Для этого, прежде всего, определяется дисперсия адекватности:

.

(6.14)

Здесь  расчетное значение отклика у;

y_j  наблюдаемое в ходе эксперимента значение отклика;

k  количество коэффициентов, включенных в уравнение регрессии; соответствует числу степеней свободы.

Следующим этапом проверки адекватности является сопоставление дисперсии адекватности с дисперсией эксперимента:

.

(6.15)

Здесь  оценка математического ожидания наблюдений у.

Расчетный критерий Фишера вычисляется по следующей формуле:

.

(6.16)

Наблюдаемое значение сопоставляется с критическим для выбранного уровня значимости q и соответствующих степеней свободы, которые для числителя выразятся как ₁ = n – k, а для знаменателя – ₂ = n – 1: .

Если наблюдаемое значение меньше критического, то модель можно признать адекватной. Иначе необходимо увеличить степень полинома регрессии, введя дополнительный член уравнения. Кроме того, необходимо учесть, что оценки коэффициентов регрессии будут приближаться к истинным значениям по мере увеличения числа опытов. Поэтому в некоторых случаях за счет увеличения числа опытов можно достигнуть адекватности модели.

Пример 6.1. Количество выпускаемой продукции y зависит от двух факторов: х₁ – количества бригад, занятых выпуском продукции, и х₂ – прибыли от реализации продукции (млн руб.). Требуется определить функцию зависимости y = f (х₁, х₂) по результатам наблюдений, приведенных в табл.6.1, и проверить адекватность полученной модели.

Таблица 6.1. Исходные данные к примеру 6.1

Наблюдения	x0 (фиктивная переменная)	х1	х2	y
1	1	1	2	4
2	1	3	3	3
3	1	2	4	3
4	1	1	3	2

Решение. Искомое уравнение будет иметь вид

Запишем исходные данные в виде матриц:

, , .

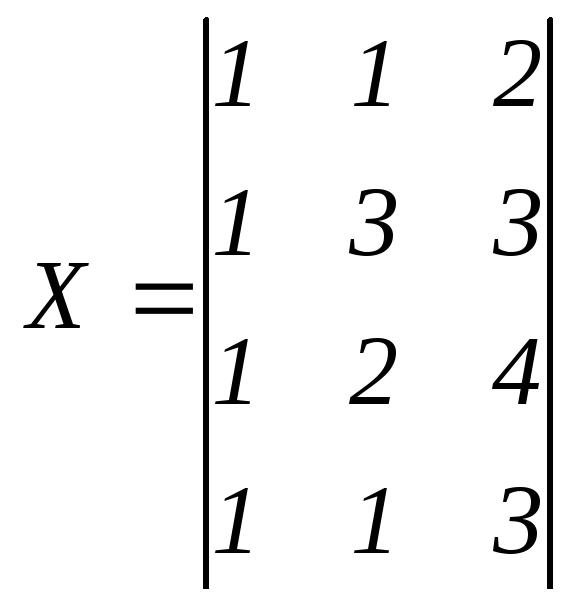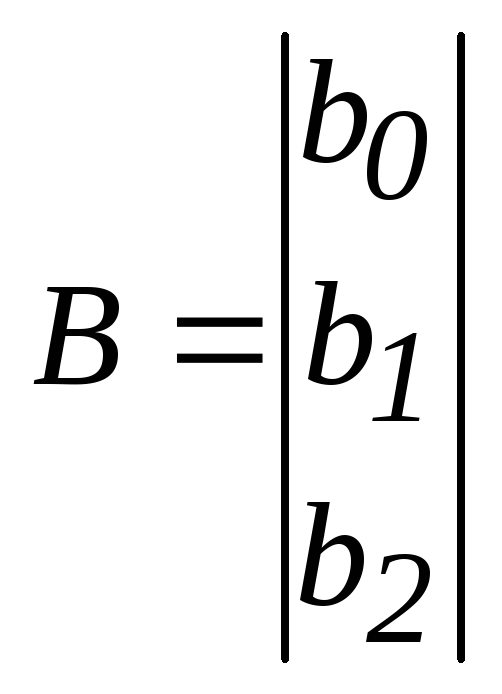Вычислим С:

.

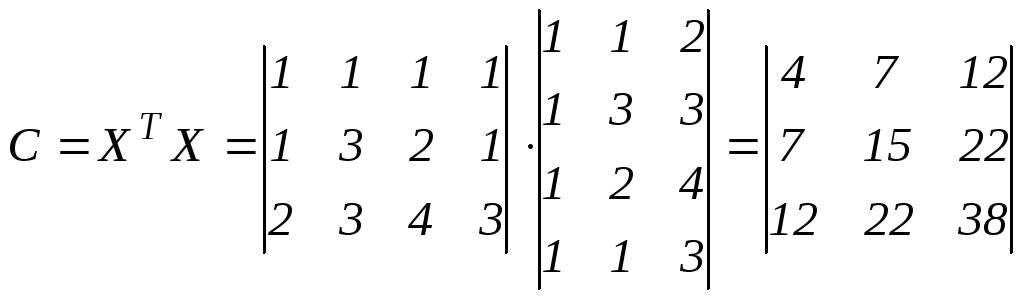Определитель

 = 4(15 38 – 22  22) – 7(7 38 – 12 22) + 12((7 22 – 15 12) = 18.

По формуле (6.10) определим:

;

, .

Таким образом, получаем модель

.

Значения y, полученные по модели,

.

Дисперсия адекватности (6.14)

.

Дисперсия эксперимента (6.15)

,

где = (4 + 3 + 3 +2)/4 = 3.

Расчетный критерий Фишера вычисляется по формуле

.

Критическое значение . Так как, то гипотеза об адекватности модели принимается.

Задания для самостоятельной работы

1. Для условия задачи 6.1 определите функцию зависимости y = f (х₁, х₂) по результатам наблюдений, приведенным в табл. 6.2, и проверьте адекватность полученной модели.

Таблица 6.2. Исходные данные

Наблюдения	х0 (фиктивная переменная)	х1	х2	y
1	1	1	2	4
2	1	3	3	3
3	1	2	4	3
4	1	2	3	1

2. Сформулируйте задачу аналитической обработки экспериментальных данных методом регрессионного анализа. Подготовьте выборку исходных данных и приведите решение матричным методом.
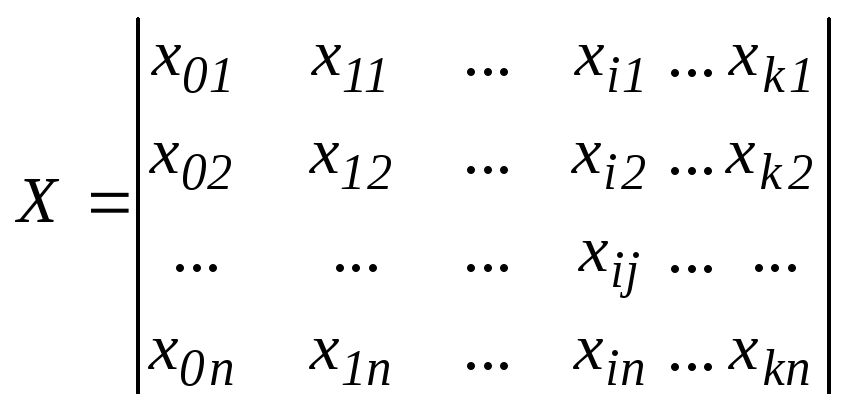
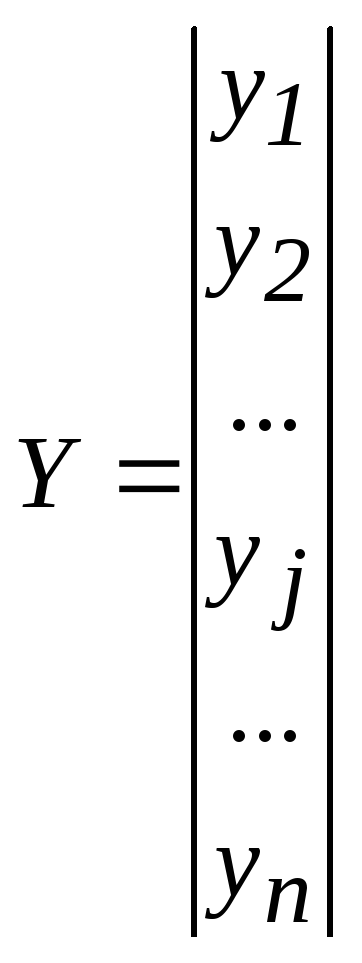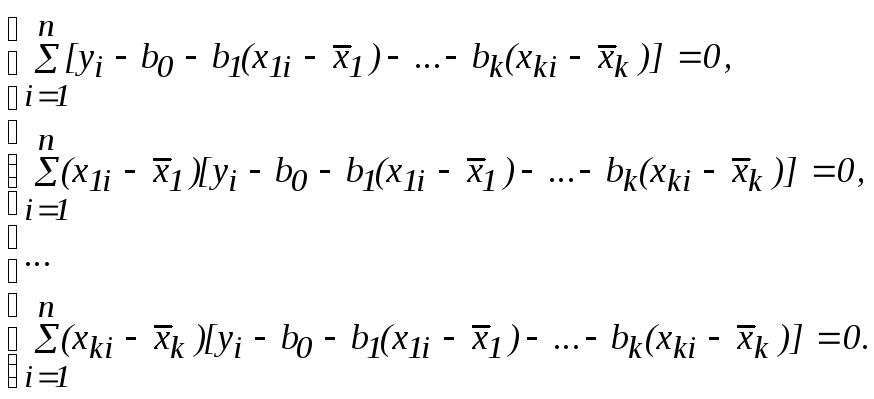
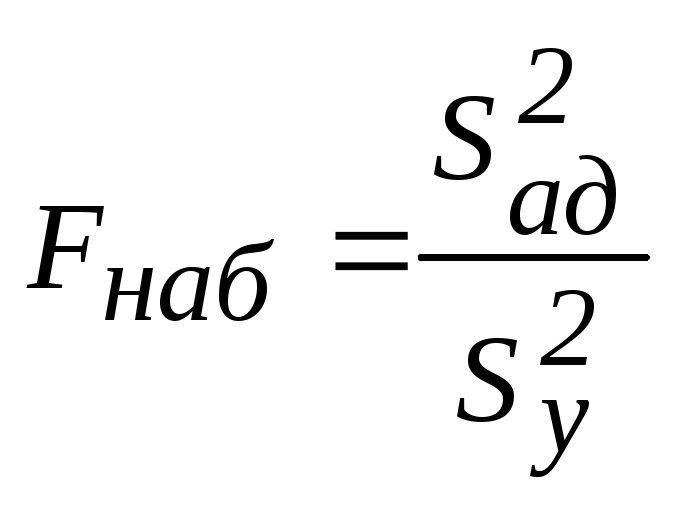