1.1. Интерполяция по Лагранжу
При интерполяции по Лагранжу задают n + 1 табличное значение (xi,fi), гдеi= 0, 1, .. ,n. Предположим, что точки (xi,fi) принадлежат кривойf =f(x) в интервалеx0xxn. Интерполяционный многочлен для этого метода имеет вид:
Ln(x) =f0Ф0(x) +f1Ф1(x) + ...+fnФn(x),
где все Фj(x) – многочлены степениn, коэффициенты которых можно найти с помощьюn + 1 уравнений:Ln(xi) =fiприi= 0, 1, .. ,n.
В результате получим систему уравнений:
x=x0,Ln(x=x0) =f0;f0Ф0(x0) +f1Ф1(x0) + ...+fnФn(x0) =f0;
. . .
x=xn,Ln(x=xn) =fn;f0Ф0(xn) +f1Ф1(xn) + ...+fnФn(xn) =fn.
Если значения Фj(xi) выбраны так, что
,
(т. е. Фj(xj) = 1), то выписанные выше уравнения будут удовлетворены. Это условие означает, что любой многочлен Фj(x) равен нулю при каждомxiкромеxj. Следовательно, в общем случае многочлен Фj(x) имеет вид:
Фj(x) =Cj(x–x0) (x–x1) ... (x–xj – 1) (x–xj + 1) ... (x–xn).
Так как Фj(xj) = 1, то коэффициентCjопределяется выражением:
;
.
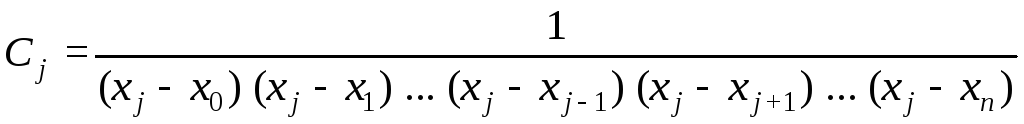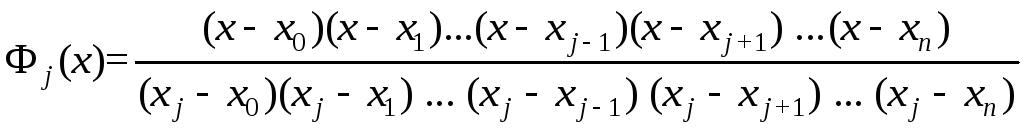Наконец для искомого многочлена получаем
.
Введя обозначения:
Lj(x) = (x–x0) (x–x1) ... (x–xj – 1) (x–xj + 1) ... (x–xn),
можем записать полученный многочлен в более компактном виде:
.
Основным преимуществом лагранжевой интерполяции является её простота и быстрота.
1.2. Метод разделённых разностей
Существует множество разностных методов интерполяции, однако наиболее распространён метод Ньютона для интерполирования вперёд, известный также как метод Ньютона-Грегори. Интерполяционный многочлен для этого имеет вид [1]:
Pn(x) = c0 + c1(x – x0) + c2(x – x0)(x – x1) + ... +cn(x–x0)(x–x1) ... (x–xn – 1).
Коэффициенты сjнаходят из уравненийPn(x) =yiприi= 0, 1, ... ,n, позволяющих записать систему:
Pn(x = x0) = c0 + c10 + c20(x0 – x1) + ... +cn0(x0 – x1) ... (x0 – xn – 1);
Pn(x = x1) = c0 + c1(x1 – x0) + c2(x1 – x0)0 + ... +cn(x1 – x0)0... (x1 – xn – 1);
. . .
Pn(x = xn) = c0 + c1(xn – x0) + c2(xn – x0)(xn – x1) + ... +
+ cn(xn – x0)(xn – x1) ... (xn – xn – 1).
Отсюда:
c0=y0,x=x0;
c0 + c1 (x1 – x0) = y1, x = x1, (x1 – x0) = h;
c0 + c1 (x2 – x0) + c2 (x2 – x0)(x2 – x1) = y2, x = x2, (x2 – x1) = h, (x2 – x0) = 2h;
. . .
c0 + ... +cn (xn – x0) (xn – x1) ... (xn – xn-1) = yn, x = xn, xn – x0 = nh,
xn – x1 = (n – 1)h,…, xn – xn – 1 = h.
Эта линейная система уравнений с треугольной матрицей, и определение с её помощью значений cj не вызывает затруднений. Однако существует ещё более простой способ определенияcj, основанный на применении правых конечных разностей. Если значенияxзаданы через равные промежуткиxi + 1–xi =h, то в общем случаеxi =x0+ih, гдеi= 1, 2, ... ,n. Последнее выражение позволяет привести решаемые уравнения к виду:
y0 = c0;
y1 = c0 + c1h;
y2 = c0 + c12h + 2h2c2;
. . .
yi = c0 + c1ih + c2ih[(i – 1)h] + ... +ci (i!)hi,
откуда для коэффициентов получаем:
c0 = y0;
c1 = (y1 – c0)/h = (y1 – y0)/h = y0/h .
y0называется первой правой разностью. Продолжая вычисления, находим:
c2= (y2–c0–c12h)/2h2= [(y2–y1) – (y1–y0)]/2h2= [(y0)]/2h2=2y0/2h2,
где 2y0 – вторая правая разность, представляющая собой разность разностей. Коэффициентcjможно представить в виде:
cj = jy0/(j!)h j.
В общем случае разности более высоких порядков для функции y=f(x) в интервалеx0x xnопределяются выражением:
jyi= j – 1yi + 1– j – 1yi,
где i = 0, 1, ... ,n –j. Часто их сводят в таблицы, где разности порядкаnвыражены через разности порядкаn – 1 (табл. 2.2).
Интерполяция вперед:
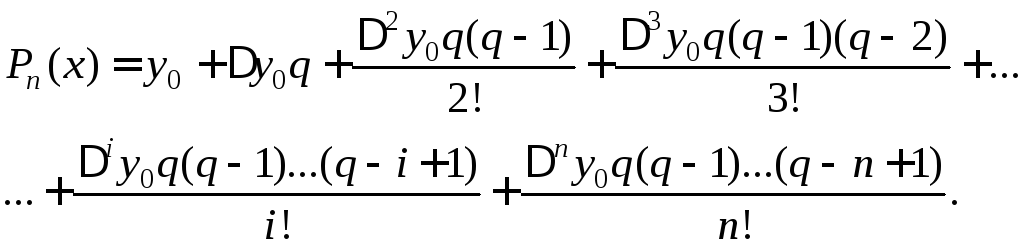
Интерполяция назад:
.
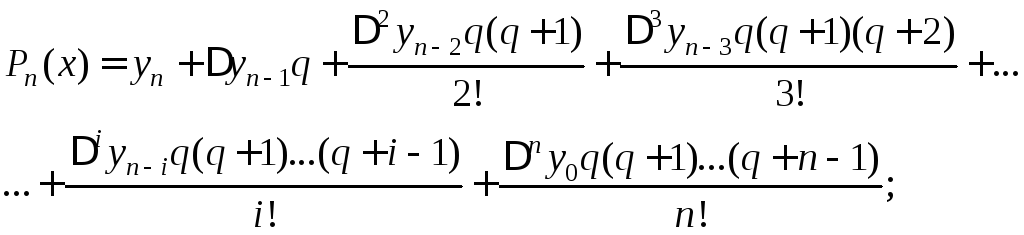
Таблица 2.2
Правые разности
|
xi |
yi |
yi= yi + 1 – yi |
2yi = = yi + 1 – yi |
3yi = = 2yi + 1 – 2yi |
4yi = = 3yi + 1 – 3yi |
5yi = = 4yi+ 1 – 4yi |
|
x0 |
y0 |
|
|
|
|
|
|
|
|
y0 |
|
|
|
|
|
x1 |
y1 |
|
2y0 |
|
|
|
|
|
|
y1 |
|
3y0 |
|
|
|
x2 |
y2 |
|
2y1 |
|
4y0 |
|
|
|
|
y2 |
|
3y1 |
|
5y0 |
|
x3 |
y3 |
|
2y2 |
|
4y1 |
… |
|
|
|
y3 |
|
3y2 |
… |
|
|
x4 |
y4 |
|
2y3 |
… |
|
|
|
|
|
y4 |
… |
|
|
|
|
x5 |
y5 |
… |
|
|
|
|
|
… |
… |
|
|
|
|
|