1.5. Сглаживание с помощью сплайнов

Сплайны лишь недавно стали использовать в вычислительнойматематике. Однако в машиностроительном черчении они фактически применяются уже давно, т. к. сплайн – это в переводе не что иное, как «гибкая линейка», которую деформируют так, чтобы по ней можно было провести кривую через заданные точки (x_i,у_i).Сплайн (или сплайн-функции) – функция с кусочной структурой и повторяющимся на каждом звене (отрезке) строением, но с различными значениями параметров.

Кубическийсплайн– это группа сопряженных кубических многочленов, в местах сопряжениякоторых первая и вторая производные непрерывны. Чтобы построить кубический сплайн, необходимо задать коэффициенты, которые единственным образом определяют кубический многочлен в промежутке между данными точками. Например, в случае,представленном на рис. 1, необходимо задать все кубические функции q₁(х), q₂(х), . . ., q_m(х).

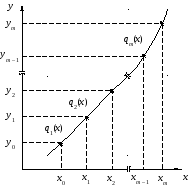
Рис. 1. Кубический сплайн

В наиболее общем случае эти многочлены имеют вид:

q_i (х) = k_1i + k_2i x + k_3i x² + k_4i x³, i=1, 2, . . ., m,

где k_ji – постоянные, определяемые указанными ниже условиями.

Первые 2т условий требуют, чтобы сплайны соприкасалисьв заданных точках. Эти условия имеют вид:

q_i (x) =y_i;i = 1,…,m;

q_{i + 1}(x_i) =y_i;i = 0,…,m – 1.

Следующие 2m– 2 условий требуют, чтобы в местах соприкосновения сплайнов были равны первые и вторые производные:

q_i₊₁(x_i) = q_i(x_i), i = 1,…, m – 1;

q_i₊₁(x_i) = q_i(x_i), i = 1,…, m – 1.

Система алгебраических уравнений имела решение тогда, когда число уравнений точно равно числу неизвестных. На данном этапе мы имеем 4mнеизвестных и 4m– 2 уравнений. Следовательно, мы должны найти еще два уравнения. Обычно используют уравнения

q₁(x₀) = 0 иq_m(х_m) = 0.

Полученный таким способом сплайн называют естественным кубическим сплайном. Найдя коэффициенты сплайна, эту кусочно-гладкую полиноминальную функцию можно использовать для представления данных при интерполяции, подгонке кривой или поверхности.

На первый взгляд может показаться, что определение коэффициентов сводится к решению 4m уравнений с 4m неизвестными. Однако, специально выбрав вид кубических многочленов, можно значительно упростить задачу. Если отдельные кубические уравнения имеют вид:

q_i (x) =ty_i +t_ср.y_{i – 1}+x_i[k_{i – 1}–d_i)tt²_ср.– (k_i–d_i)t²t_cp.],

где i = 1,..., m;

x_i = x_i – x_{i – 1};

t = (x – x_{i – 1})/x_i;

t_cp. = 1 – t;

у_i = y_{i – 1};

y_i/x_i = d_i ,

то каждое из уравнений q_i (x)содержит только два постоянных неизвестных коэффициента. После того как первое уравнение q_i (x) записано, с каждым следующим уравнением добавляетсятолько один новый неизвестный коэффициент. При этом при x = x_i – 1 t = 0, t_cp. = 1, а при х = x_i t_cp. = 0, t = 1. Следовательно, при таком выборе кубических многочленов автоматически удовлетворяются все условия, кроме условий, налагаемых на вторые производные. Последние условия для внутренних точек выражаются соотношениями:

k_{i – 1}x_{i + 1} + 2k_i (x_i + x_i + 1) + k_{i + 1}x_i = 3(d_ix_i + 1 + d_i + 1x_i),

а для двух внешних – соотношениями:

2k₀ + k₁ = 3d_l и k_m – 1 + 2k_m – l = 3d_m.

Таким образом, решаемая система уравнений является линейной, а ее матрица – трехдиагональной:

В этой системе уравнений число определяемых коэффициентов равно числу заданных точек. Поэтому решение оказывается не более сложным, чем в случае аппроксимации т + 1 точек многочленомm-й степени. Часто оказывается, что кубический сплайн аппроксимирует функцию лучше, чем многочлен степенит.

.

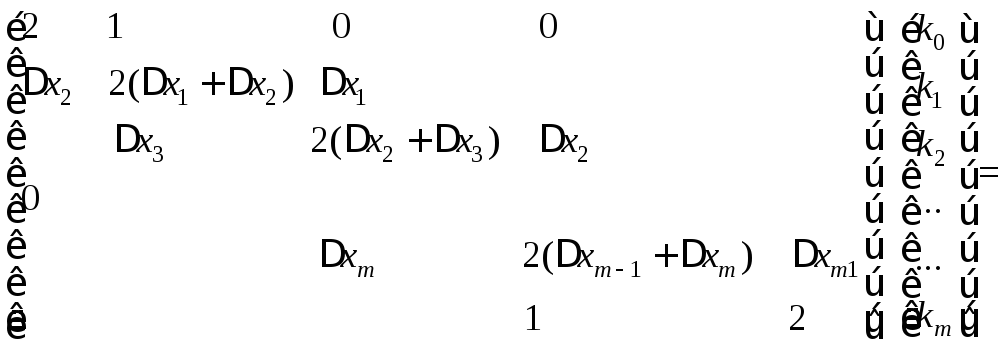
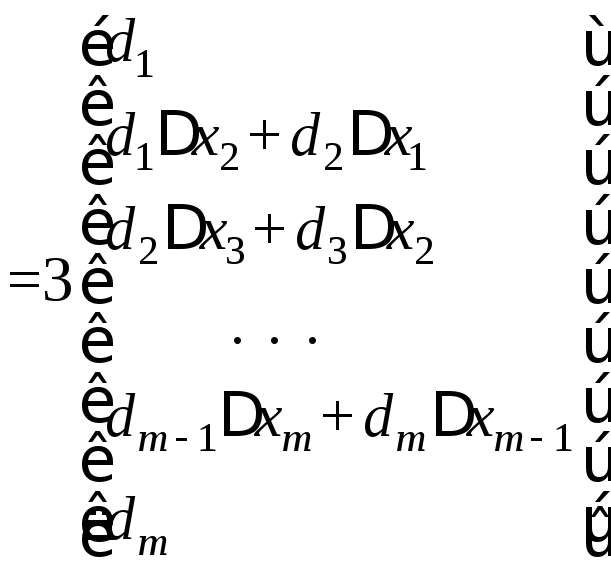Следует отметить, что существуют и другие сплайны, получающиеся при других условиях на концах или при использовании многочленов более высоких степеней.