1.8. Интегрирование по методу Ромберга

Из всех формул Ньютона-Котеса метод трапеций является наиболее простым, однако он не даёт достаточной степени точности. Метод Ромберга получил широкое распространение, поскольку сочетает в себе простоту метода трапеций с высокой точностью вычисления [1]. Он состоит в применении экстраполяционного метода Ричардсона для улучшения результатов, полученных с помощью метода трапеций. Для интегрирования по методу Ромберга вспомним метод трапеций:

,

где h= (b –a)/mиx_j=a+jh. Известно, что погрешность усечения уменьшается с увеличением числа шаговm. Один из способов повышения систематического повышенияmсостоит в использовании прогрессии вида:

m = 2^{k – 1}, k = 1, 2, ... , n,

где n– целое положительное число. Шагhдля такой прогрессии уменьшается как:

h_k = b – a/2^{k – 1}, k = 1, 2, ..., n.

h₁ = b – a/2^{1 – 1} = b – a/1, отсюда m = 1

h₂ = b – a/2^{2 – 1}= b – a/2, m = 2

h₃ = b – a/2^{3 – 1}= b – a/4, m = 4

Удобно обозначить R_k,1приближённое значение интеграла, тогда:

R_1,1 = (h₁/2)[f(a) + f(b)], (k = 1, m = 1);

R_2,1 = (h₂/2)[f(a) + f(b) + 2f(a + h₂)], (k = 2, m = 2);

R_3,1 = (h₃/2)[f(a) + f(b) + 2[f(a + h₃) + f(a + 2h₃) + f(a +3h₃)]], (k = 3, m = 3).

Можно показать, что эта последовательность записывается в общем виде как:

,

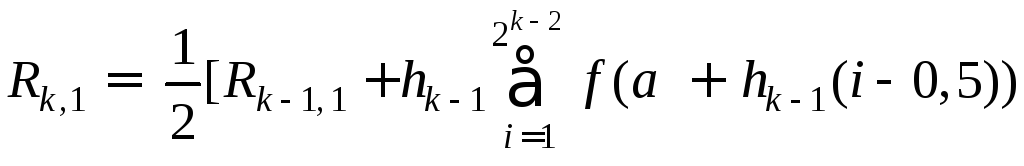для каждого k = 2, 3, ... ,n. Это выражение можно использовать для ускорения процесса вычисления каждогоR_k,1. В то время какkувеличивается, точностьR_k,1также увеличивается, однако сходимость к точному значению интеграла очень медленная. Для ускорения процесса сходимости используют экстраполяционную формулу Ричардсона:

R_ij= [2^{2(j – 1)}R_{i,j – 1} –R_{i – 1,j – 1}]/(2^{2(j – 1)}– 1).

для каждого i= 2, 3, ... ,n;j= 1, 2, ... ,i, где экстраполированное значение, отвечающее большему индексуj, соответствует более старшему порядку в формулах Ньютона-Котеса (рис. 2).

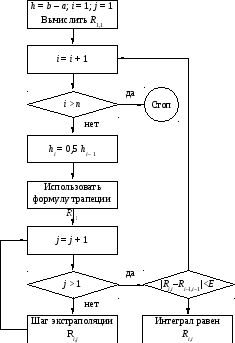
Рис. 2. Алгоритм интегрирования по формулам Ньютона-Котеса

Результат аппроксимаций может быть записан в виде треугольной матрицы:

R_1,1

R_2,1R_2,2

R_3,1R_3,2R_3,3

R_4,1R_4,2R_4,3R_4,4

. . .

R_n,1R_n,2...R_n,n

Диагональные элементы сходятся к точному значению интеграла быстрее, чем R_n,1. Обычно процедура применения итерационной схемы метода Ромберга заключается в последовательном нахождении элементов в строчках до тех пор, пока для некоторогоnразность междуR_n,nиR_{n – 1,n – 1} меньше некоторой наперёд заданной погрешности.

1.9.Квадратурные формулы Гаусса

Все формулы интегрирования Ньютона-Котеса используют равноотстоящие координаты абсцисс. Если это ограничение снято, расстояние между точками можно выбрать таким образом, чтобы понизить погрешность аппроксимации.

В выражении:

,

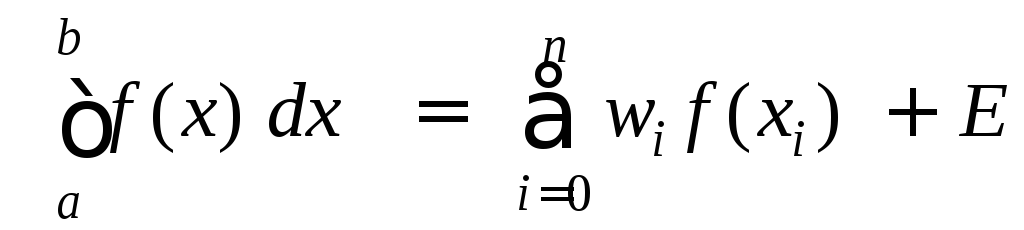w_iиx_iвзяты неизвестными, подлежащими определению. Таким образом, полное число неизвестных параметров равно 2(n + 1). Полином степени 2n + 1 для своего однозначного определения требует задания 2n + 2 узлов.

Будем аппроксимировать интеграл, используя полином степени 2n + 1, и потребуем, чтобы для всех полиномов со степенями, равными или меньшими этого значения, погрешности аппроксимации были равны нулю. Это условие даст 2n + 2 уравнений для 2n + 2 неизвестных. В общем случае конечные уравнения окажутся линейными относительноw_i, но нелинейными относительноx_i. Если пределы интегрирования составляют [–1, 1], значениямиx_iстанутn+ 1 корней полинома ЛежандраP_n + 1(x) = 0. После того как найденыx_iвеличиныw_iмогут быть найдены методами решения линейных систем. Рассмотрим случай сn = 1. Требование, чтобы ра­венство

,

удовлетворялось для всех полиномов степени 2n + 1 и меньше, означает, что дляf(x) = 1,x,x²иx³равенство должно строго выполняться. Из этого получаем следующие уравнения:

;

;

;

.

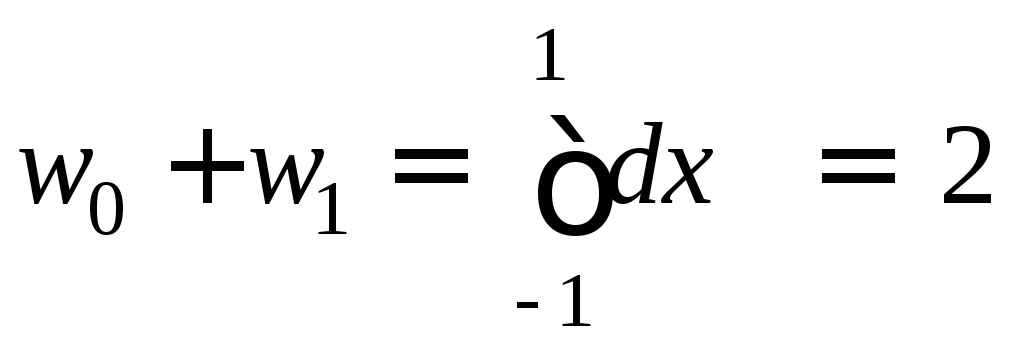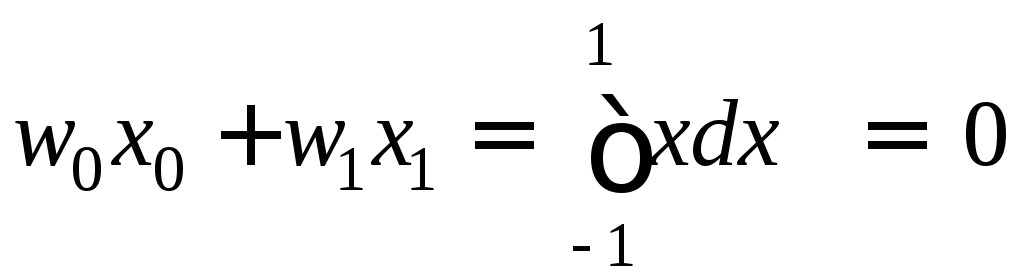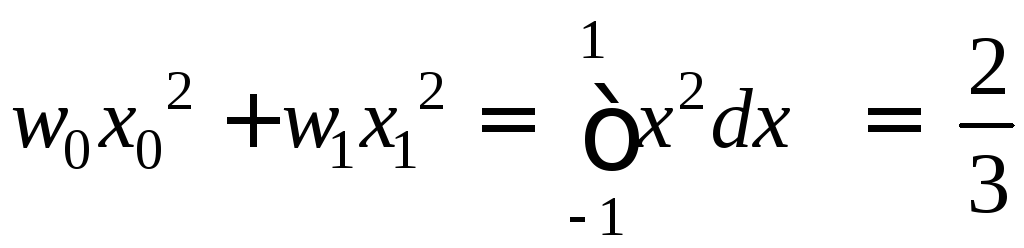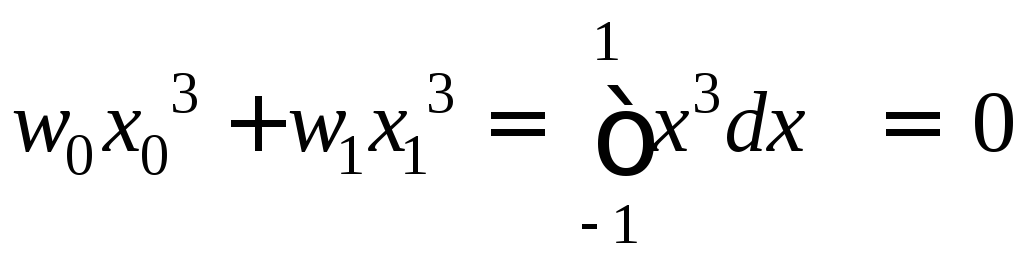Система четырёх уравнений для четырёх неизвестных может быть решена даже для нелинейных уравнений. Чтобы избежать трудностей, связанных с нелинейностью, возьмём полином Лежандра в виде:

P²(x) = –1 + 3x².

Преимуществом подобной схемы является то, что корни полиномов Лежандра хорошо известны и табулированы в литературе.

Полином второй степени имеет корни и. Используя эти значения и два любых уравнения из выше приведённых, получим, чтоw₀ = 1 иw₁=1. Тогда интеграл записывается в виде:

_.

Ограничение, связанное с необходимостью выбора промежутка интегрирования от –1 до 1 не настолько затруднительно. Очевидно, что замена переменных z= 2x– (a+b)/(b–a) преобразует интеграл к требуемому виду:

.

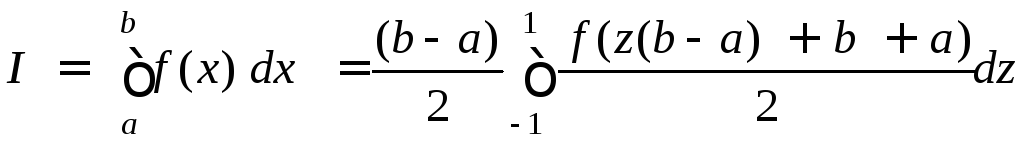Таким образом, применение метода квадратур Гаусса с n= 2 для вычисления интеграла даёт:

I = (b – a)/2 [w₁f([(b – a)z₁ + b + a]/2) + w₂f([(b – a)z₂ + b + a]/2)].

Для функции с n= 3 результат окажется следующим:

I = (b – a)/2 [w₁f([(b – a)z₁ + b + a]/2) + w₂f([(b – a)z₂ + b + a]/2) +

+ w₃f([(b–a)z₃+b+a]/2)].

Задача, таким образом, состоит в нахождении коэффициентов w_iи корней полинома Лежандраz_i. Эти значения приведены в табл. 

Таблица

Значения коэффициентов и корней для формул Гаусса [1]

n	Корни	Коэффициенты	n	Корни	Коэффициенты
2	0,5773502692 –0,5773502692	1,0000000000 1,0000000000	8	0,9602898565 0,7966664774 0,5255324099 0,1834346425 –0,1834346425 –0,5255324099 –0,7966664774 –0,9602898565	0,1012285363 0,2223810345 0,3137066459 0,3626837834 0,3626837834 0,3137066459 0,2223810345 0,1012285363
3	0,7745966692 0,0000000000 –0,7745966692	0,5555555556 0,8888888889 0,5555555556
4	0,8611363116 0,3399810436 –0,3399810436 –0,8611363116	0,3478548451 0,6521451549 0,6521451549 0,3478548451
5	0,9061798459 0,5384693101 0,0000000000 –0,5384693101 –0,9061798459	0,2369268850 0,4786286705 0,5688888889 0,4786286705 0,2369268850	9	0,9681602395 0,8360311073 0,6133714327 0,3242534234 0,0000000000 –0,3242534234 –0,6133714327 –0,8360311073 –0,9681602395	0,0812743884 0,1806481607 0,2606106964 0,3123470770 0,3302393550 0,3123470770 0,2606106964 0,1806481607 0,0812743884
6	0,9324695142 0,6612093864 0,2386191861 –0,2386191861 –0,6612093864 –0,9324695142	0,1713244924 0,3607615730 0,4679139346 0,4679139346 0,3607615730 0,1713244924
7	0,9491079123 0,7415311856 0,4058451414 0,0000000000 –0,4058451414 –0,7415311856 –0,9491079123	0,1294849661 0,2797053914 0,3818300505 0,4179591837 0,3818300505 0,2797053914 0,1294849661	10	0,9739065285 0,8650633667 0,6794095683 0,4333953941 0,1488743390 –0,1488743390 –0,4333953941 –0,6794095683 –0,8650633667 –0,9739065285	0,0666713443 0,1494513492 0,2190863625 0,2692667193 0,2955242247 0,2955242247 0,2692667193 0,2190863625 0,1494513492 0,0666713443