1.6. Дифференцирование с использованием формул разностей

Возьмём интерполяционный многочлен второй степени в таком виде, чтобы он проходил через три соседние точки (x₀,y₀), (x₁,y₁) и (x₂,y₂):

.

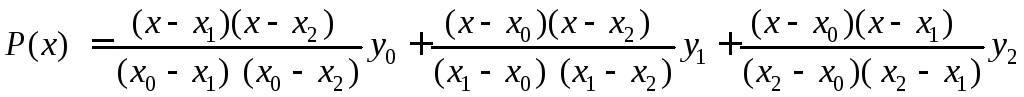Первая производная этого выражения имеет вид:

.

Если это выражение вычислить при x=x₀, результатом окажется значение первой производной, полученное по левым разностям. Если это выражение вычислить приx=x₁, найдём первую производную по центральным разностям. Приx=x₂получим производную по правым разностям. Формулы с центральной разностью неприменимы для начальной и для конечных точек в таблице данных.

Для более точных значений левой, центральной и правой разностей при нахождении производных можно использовать аппроксимирующие многочлены старшей степени с более чем тремя узлами. Кроме того, приближенные значения производных более высокого порядка найдены дифференцированием полученных многочленов.

При равностоящих друг от друга значениях xвыражения для приближённых вычислений производных упрощаются. Если шаг составляетx₁ –x₀=h, приближение правой разностью для производной в точкеx₀есть

P(x) = (–3y₀+ 4y₁–y₂)/(2h).

Для оценки величины ошибок аппроксимации используем разложение в ряд Тейлора в виде:

f(x+ζ) =f(x) +ζ/1!f (x) +ζ²/2!f (x) +ζ³/3!f (x) + ... .

Если x=x₀и=h(единичный шаг), тоf(x₀+h) =y₁. Тогда

y₁=y₀+hD(y₀) + (h²/2)D²(y₀) + (h³/6)D³(y₀) + ... .

Аналогично, если = 2h, получаем

y₂=y₀+ 2hD(y₀) + 4(h²/2)D²(y₀) +8(h³/6)D³(y₀) + ... .

Избавляясь от второй производной в этих уравнениях домножением первого из них на 4, второго на –1 и затем, складывая их, получаем в итоге:

D(y₀) = (4y₁–y₂– 3y₀)/(2h) +h²y₀/3.

Найденное второе приближение первой производной совпадает с вычисленным ранее, за исключением слагаемого h²y₀/3, характеризующего погрешность.

Аналогичная процедура может быть применена для нахождения производной с более высоким приближением для левой, центральной и правой разностей наряду с вычислением соответствующих погрешностей.

Приближённые формулы дифференцирования пятых разностей [1]:

1) y₀

(–3y₄+16y₃– 36y₂+ 48y₁– 25y₀)/12hлевая;

(–y₂+ 8y₁– 8y_–1+y_–2)/12hцентральная;

(3y_–4– 16y_–3+ 36y_–2– 48y_–1+ 25y₀)/12hправая;

2) y₀

(11y₄ – 56y₃ + 114y₂ – 104y₁ + 35y₀)/12h²;

(–y₂ + 16y₁ – 30y₀ + 16y_–1 – y_–2)/12h²;

(11y_–4 – 56y_–3 + 114y_–2 – 104y_–1 + 35y₀)/12h²;

3) y₀

(–3y₄ + 14y₃ – 24y₂ + 18y₁ – 5y₀)/2h³;

(y₂ – 2y₁ +2y_–1 – y_–2)/2h³;

(3y_–4 – 14y_–3 + 24y_–2 – 18y_–1 + 5y₀)/2h³.

1.7. Интегрирование по методу Симпсона

Одним из путей уменьшения ошибки в процессе численного интегрирования является использование иного, чем прямая линия (метод трапеций), вида аппроксимирующей кривой на малом отрезке интегрирования. Из этого предположения естественным образом следует, что нужно взять кривую более старшего порядка, а именно параболу. Разумеется, парабола требует уже не двух, а трёх соседних точек табулированных значений, так что в результате формула для интеграла будет другой, чем в методе трапеций. Новая формула, известная как формула Симпсона, имеет вид [1]:

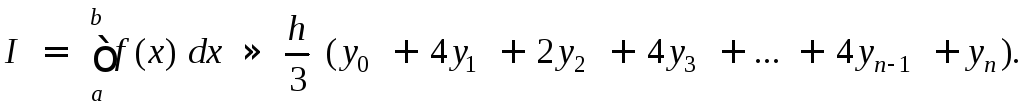
Это равенство применяют для чётного числа промежутков. Погрешность усечения в методе Симпсона может быть представлена в виде:

E = –(x_{i + n} – x_i)* h⁴ * f ^IV_ср. /180,

где f ^IV_ср.означает среднее значение четвёртой производной функцииf(x) на промежутке (x_i,x_i + n). Суммарная погрешность пропорциональна четвёртой степени интервала разбиения. Это означает, что при делении интервала пополам – погрешность уменьшается в 16 раз. Такой метод, безусловно, имеет преимущества по сравнению с методом трапеций.

При использовании метода Симпсона может случиться так, что количество промежутков нечётно. Этой трудности можно избежать, если для первых трёх промежутков применять следующую формулу, использующую параболу третьей степени, проходящую через четыре первые точки:

A₃= (3h/8)(y₀+ 3y₁+ 3y₂+y₃).

Эта формула известна как формула Симпсона трёх восьмых.