1.3. Итерационные методы интерполяции
Эти методы основаны на повторном применении простой интерполяционной схемы. Наиболее известным из них является метод Эйткена, сущность которого состоит в повторном применении линейной интерполяции.
Линейная интерполяция между точками (x0,y0) и (xi,yi) осуществляется по формуле [1]:
yi1(x) = (xi – x0)–1[y0(xi – x) – yi (x0 – x)],
с помощью которой, задав значение xi, можно составить таблицу функцийyi1(x), гдеi= 1, 2, ... ,n. Пользуясь этими функциями, с помощью линейной интерполяции:yi2(x) = (xi –x1)–1[y11(x)(xi –x) –yi1(x)(x1–x)], получим новое семейство соотношений. Простой подстановкой можно показать, что выражение дляyi2(x) представляет собой многочлены второй степени, описывающие кривые, проходящие через точки (x0,y0), (x1,y1) и (xi,yi). Получив многочленыyi2с помощью линейной интерполяции и, используя функцииyi2(x), можно записать выражение для многочлена третьей степени:yi3(x) = = (xi –x2)–1[y22(x)(xi–x) –yi2(x)(x2–x)], описывающего кривые, проходящие через точки (x0,y0), (x1,y1), (x2,y2) и (xi,yi). Продолжая этот процесс, получим значенияyij(x), которые будут стремиться к значениюf(x). Хотя в принципе этот метод позволяет вводить многочлены степениn 3, обычно стремясь избежать роста ошибок, этого не делают. Следует, однако, отметить, что метод Эйткена не требует, чтобы используемые для интерполяции значения функции были расположены через равные интервалы (h ≠ const).
1.4. Метод наименьших квадратов для функций
Пусть функция задана n + 1 точками (x0,y0), (x1,y1), ... , (xn,yn) и требуется найти аппроксимирующую кривуюG(x) в диапазонеx0xxn. В этом случае погрешность в каждой точке составит:
Тогда сумма квадратов погрешностей определится выражением:
.
Обычно функцию G(x) выбирают в виде линейной комбинации:
G(x) = c1G1(xi) + c2G2(xi) + ... +ckGk(xi).
Условие минимума Еопределяются из уравнений частных производных, приравненных к нулю:
.
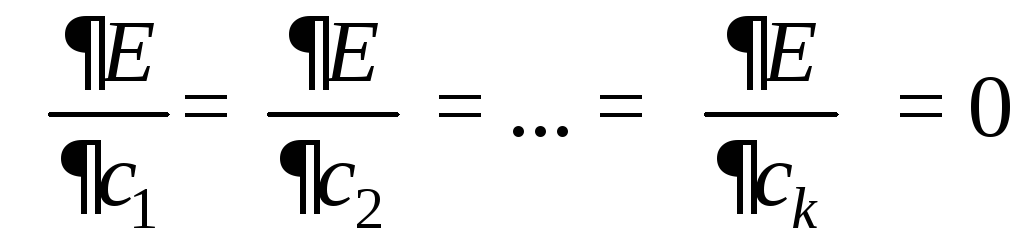Поскольку
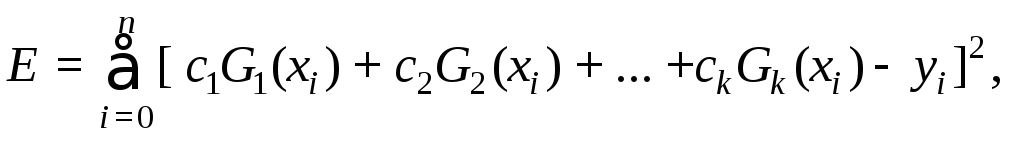
то это условие эквивалентно системе уравнений
.
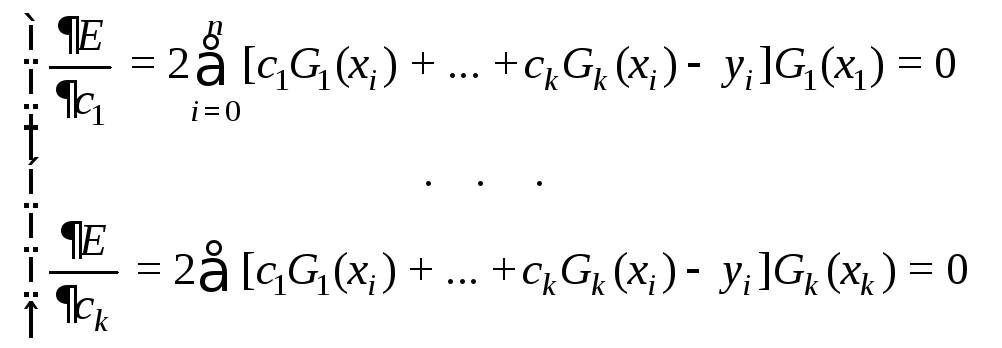Эти kуравнений, очевидно после открытия скобок, можно представить в виде:
.
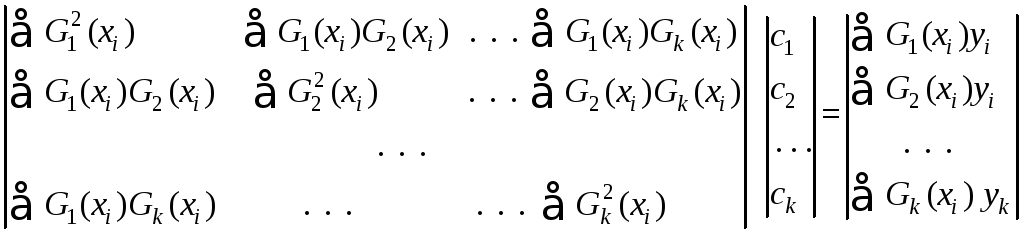Так как элементы матрицы в левой части и вектор-столбца в правой определяются табличными данными, то выписанная система kлинейных уравнений сkнеизвестными может быть решена. Можно выбрать любую функциюGi(x), лишь бы она была линейной относительно своих коэффициентов (например,ax +b). Фактический выбор функцииGi(x) должен осуществляться с учётом специфики табличных данных, под которой понимается их периодичность, экспоненциальный или логарифмический характер, свойства симметрии и наличие асимптотики.
Иногда таблицу разбивают на несколько частей и подбирают отдельную аппроксимирующую кривую для каждой части, в тех случаях, когда есть основания полагать, что аппроксимируемые данные соответствуют разным физическим состояниям системы. Пользуясь приближённой формулой, не следует выходить за пределы интервала, в котором она справедлива.
Если при построении аппроксимирующей функции в качестве Gi(x) используют ортогональные полиномы, для которых
Gj(xi)Gk(xi) = 0 при j i,
то матрица выписанной выше системы уравнений окажется диагональной, а выражения для коэффициентов cjупростятся:
.
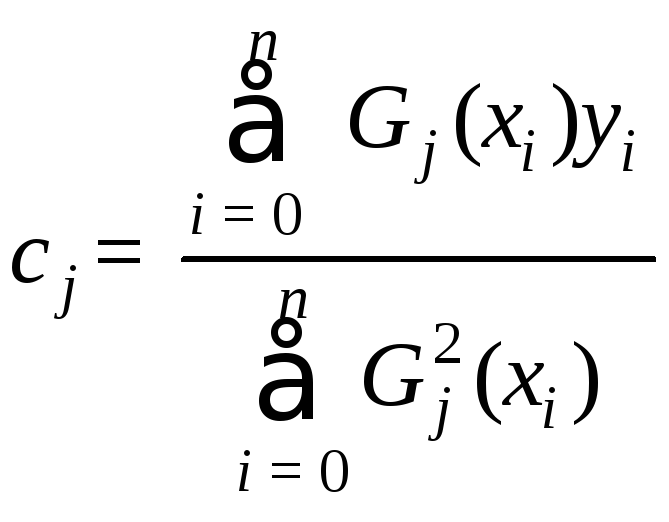Это существенно облегчает задачу, и именно во многих стандартных программах подгонки кривых используют ортогональные полиномы.