1.1.3.2. Маятники

Под маятником понимают твёрдое тело, которое совершает под действием силы тяжести колебания вокруг неподвижной точки или оси. Различают физический и математический маятники.

Математический маятник – это идеализированная система, состоящая из невесомой нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной материальной точке.

Математическим маятником, например, является шарик на длинной тонкой нити.

Отклонение маятника от положения равновесия характеризуется углом φ, который образует нить с вертикалью (рис.1.15). При отклонении маятника от положения равновесия возникает момент внешних сил (силы тяжести): , гдеm– масса, – длина маятника

Этот момент стремится вернуть маятник в положение равновесия (аналогично квазиупругой силе) и направлен противоположно смещению φ, поэтому в формуле стоит знак «минус».

Уравнение динамики вращательного движениядля маятника имеет вид:Iε=,

или

.

Будем рассматривать случай малых колебаний, поэтому sin φ ≈φ, обозначим,

имеем: , или , и окончательно

.

Это уравнение гармонических колебаний, его решение:

.

Частота колебаний математического маятника определяется только его длиной и ускорением силы тяжести, и не зависит от массы маятника. Период равен:

.

_{Если колеблющееся тело нельзя представить, как материальную точку, то маятник называют физическим (рис.1.1.6). Уравнение его движения запишем в виде:}

.

_{В случае малых колебаний} , или =0 _{, где} . _{Это уравнение движения тела, совершающего гармонические колебания. Частота колебаний физического маятника зависит от его массы, длины и момента инерции относительно оси, проходящей через точку подвеса.}

_{Обозначим . Величина называется приведённой длинной физического маятника. Это длина математического маятника, период колебаний которого совпадает с периодом данного физического маятника. Точка на прямой, соединяющей точку подвеса с центром масс, лежащая на расстоянии приведённой длины от оси вращения, называется центром качания физического маятника (О’). Если маятник подвесить в центре качания, то приведённая длина и период колебаний будут теми же, что и в точке О. Таким образом, точка подвеса и центр качания обладают свойствами взаимности: при переносе точки подвеса в центр качения прежняя точка подвеса становится новым центром качения.}

_{Математический маятник, который качается с таким же периодом, как и рассматриваемый физический, называется изохронным данному физическому маятнику.}

1.1.4. Сложение колебаний (биения, фигуры Лиссажу). Векторное описание сложения колебаний

_{Сложение одинаково направленных колебаний можно производить методом векторных диаграмм. Любое гармоническое колебание можно представить в виде вектора следующим образом. Выберем ось х с началом отсчета в точке О (рис.1.1.7)}

^{Из точки О построим вектор , который составляет угол с осью х. Пусть этот вектор поворачивается с угловой скоростью . Проекция вектора на ось Х равна:}

^{то есть она совершает гармонические колебания с амплитудой а.}

^{Рассмотрим два гармонических колебания одинакового направления и одинаковой циклической малой, заданные векторами и . Смещения по оси Х равны:}

^{результирующий вектор имеет проекцию и представляет собой результирующее колебание (рис.1.1.8), по теореме косинусов Таким образом, сложение гармонических колебаний производится сложением векторов.}

^{Проведем сложение взаимно перпендикулярных колебаний. Пусть материальная точка совершает два взаимно перпендикулярных колебания частотой :}

^.

^{Сама материальная точка при этом будет двигаться по некоторой криволинейной траектории.}

^{Из уравнения движения следует:} _,

^тогда

^{. (1.1.9)}

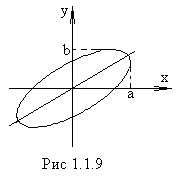
_{Из уравнения (1.1.9) можно получить уравнение эллипса (рис.1.1.9):}

_{Рассмотрим частные случаи этого уравнения:}

_{1. Разность фаз колебанийα= 0. При этом т.е. или Это уравнение прямой, и результирующее колебание происходит вдоль этой прямой с амплитудой (рис.1.1.10).}

^{2. Если разность фаз то уравнение (1.1.9) переходит в уравнение эллипса, приведенного к координатным осям, При} _{материальная точка движется по окружности, уравнение которой (рис.1.1.11).}

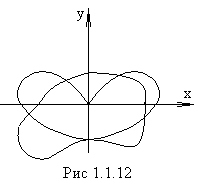
^{3. Если частоты колебаний неодинаковы, то материальная точка описывает фигуры Лиссажу (рис.1112).}

^{Рассмотрим сложение колебаний одного направления, частоты которых мало отличаются друг от друга. В этом случае результирующее движение можно рассматривать как гармоническое колебание с пульсирующей амплитудой. Такие колебания называются биениями.}

^{Пусть частота одного колебания , второго . Амплитуды обоих колебаний одинаковы и равны а. Начальные фазы равны нулю. В таком случае уравнения колебаний имеют вид:}

^{Сложим эти выражения:}

^(1.1.10)

^{График функциих(t) представлен на рис. 1.1.13. Множитель меняется гораздо медленнее, чем , поэтому (1.1.10) можно рассматривать как гармоническое колебание частоты , амплитуда которого меняется по некоторому периодическому закону}

^{Частота изменения амплитуды – частота биений – равна разности частот складываемых колебаний .}