1.3. Свободные затухающие колебания осциллятора с потерями

В любой реальной системе действуют силы трения, поэтому свободные гармонические колебания будут затухать. Затухающие колебания описываются уравнением:

(1.3.1)

где ,r– коэффициент сопротивления,k– коэффициент упругости,β– коэффициент затухания,– частота, с которой колебания совершались бы в отсутствии трения (собственная частота системы). Решение этого уравнения имеет вид:

, (1.3.2)

где α,- постоянные. Из (1.3.2) следует , что движение системы можно рассматривать как гармоническое колебание с амплитудой, меняющейся со временем по закону(рис.1.3.1).

Скорость затухания колебаний определяется коэффициентом затухания β.Пустьτ – время, за которое амплитуда уменьшается ве раз. Тогдаи, т.е. коэффициент затухания - это величина, обратная промежутку времени, за который амплитуда колебаний уменьшается ве раз.

Период колебаний: _{. Отношение амплитуд в двух соседних периодах называется декрементом затухания: .}

_{Для характеристики колебательной системы используют логарифмический декремент затухания . Тогда закон убывания амплитуды принимает вид За время} τ амплитуда уменьшается вераз, и система успевает совершитьколебаний. ИмеемиСледовательно, логарифмический декремент затухания обратен по величине числу колебаний, совершаемых за время, в течение которого амплитуда уменьшается вераз.

Время τ, за которое амплитуда уменьшается вераз, называется временем релаксации колебаний.

Другой характеристикой колебательной системы является добротность

.

Она пропорциональна числу колебаний за время релаксации.

Энергия системы пропорциональна квадрату амплитуды и при затухающих колебаниях убывает по закону

где - энергия колебаний в начальный момент времени (рис.1.3.2). Продифференцировав это выражение по времени, получим скорость убывания энергииЕсли изменение энергии за период мало, убыль энергии равнатогда

- при слабом затухании добротность пропорциональна отношению энергии, запасенной в системе в данный момент, к убыли этой энергии за один период колебаний. Добро́тность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний. Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.

С ростом коэффициента затухания период увеличивается, и при период колебаний обращается в бесконечность, т.е. движение перестает быть гармоническим.

1.4. Вынужденные колебания. Время установления вынужденных колебаний. Его связь с добротностью осциллятора

Будучи предоставлена сама себе, любая колебательная система через некоторое время остановится вследствие трения. Чтобы колебания не затухали, необходимо периодическое воздействие внешней силы. Такие колебания называются вынужденными. Если внешняя сила (вынуждающее действие) меняется по гармоническому закону, то вынужденные колебания будут гармоническими. Уравнение такого колебательного процесса

(1.4.1)

где _{β – коэффициент затухания, – собственная частота системы, , где – амплитуда вынуждающей силы, – частота изменения силы.}

_{Общее решение этого неоднородного дифференциального уравнения:}

(1.4.2)

_{где и – произвольные постоянные.}

_{Получим частные решения уравнения (1.4.1), воспользовавшись методом векторных диаграмм. Пусть частное решение имеет вид:}

(1.4.3)

_тогда

_{Подставив в (1.4.1), получаем}

(1.4.4)

_{Из выражения (1.4.4) следует, что постоянныеа и φ должны иметь такие значения, чтобы гармоническая функция была равна сумме трёх гармонических функций, стоящих в левой части уравнения. Если изобразить функцию вектором длины , направленным вправо, то функция отобразится вектором длины , повёрнутым на π/2 против часовой стрелки, а функция – вектором длины , повёрнутым относительно вектора a на π (рис.1.4.1)}

_{Сумма этих векторов (по теореме Пифагора) равна:}

_тогда

₍1.4.5₎

_{Из рисунка}

_{Подставив а и φ в (1.4.3), получим некоторое частное решение уравнения (1.4.1):}

(1.4.6)

_{Сумма общего (1.4.2) и частного (1.4.6) решений даёт решение уравнения (1.4.1), описывающего поведение системы при вынужденных колебаниях. Слагаемое (1.4.6) играет заметную роль только в начальной стадии процесса, при установлении колебаний. С течением времени из за экспоненциального множителя e}-βt _{слагаемое (1.4.2) всё больше уменьшается и далее им можно пренебречь. Таким образом, время установления вынужденных колебаний определяется временем полного затухания свободных колебаний. Функция (1.4.6) описывает установившие его вынужденные колебания с частотой, равной частоте вынуждающей силы (рис.1.4.2).}

_{Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы ω. При определённом значении ω амплитуда достигает максимума. Это явление называется резонансом, а соответствующая частота – резонансной частотой. Чтобы найти резонансную частоту, найдём максимум амплитуды (1.4.5) или, что то же самое, минимум знаменателя функции :}

Это уравнение имеет три решения: ω= 0;_{При ω = 0 имеет место максимум знаменателя. Из остальных двух решений отбрасываем отрицательное, так как ω≥0, и получаем:}

_Тогда

_{При отсутствии сопротивления среды β=0, , – резонансная частота совпадает с собственной частотой колебательной системы. Чем больше затухание β, тем меньше арез и ω.}

_{Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы называется резонансной кривой и представлена на рис.1.4.3. Из рисунка видно, что чем меньше β, тем выше и правее лежит максимум данной кривой. При очень большом затухании выражение для резонансной частоты становится мнимым и резонанс не наблюдается – с увеличением частоты амплитуда вынужденных колебаний монотонно убывает.}

_{Приω, стремящемся к нулю, все резонансные кривые стремятся к значению . Это смещение от положения равновесия, которое получает система под действием постоянной силы, равной амплитуде вынуждающей силы .}

_{При ω, стремящемся к бесконечности, все кривые асимптотически стремятся к нулю, так как при большой частоте сила так быстро меняет своё направление, что система не успевает заметно сместиться от положения равновесия.}

_{Чем меньше β, тем острее максимум амплитуды, и тем он выше. При малом затухании и тогда .}

_{Добротность равна Она показывает, во сколько раз амплитуда в момент резонанса превышает смещение системы из положения равновесия под действием постоянной силы той же величины, что и амплитуда вынуждающей силы.}

Добротность — характеристика колебательной системы, определяющая полосу резонанса и показывающая, во сколько раз запасы энергии в системе больше, чем потери энергии за один период колебаний. Она обратно пропорциональна скорости затухания собственных колебаний в системе, т.е. прямо пропорциональна времени их затухания, а, следовательно, и времени установления вынужденных колебаний. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания.

Например, в электрической резонансной цепи энергия рассеивается из-за конечного сопротивления цепи, в кварцевом кристалле затухание колебаний обусловлено внутренним трением в кристалле, в объемных электромагнитных резонаторах теряется в стенках резонатора, в его материале и в элементах связи, в оптических резонаторах - на зеркалах.

_{Вынужденные колебания отстают по фазе от вынуждающей силы на , это отставание 0≤φ≤π. Зависимость от ω для разных β имеет вид, представленный на рисунке 1.4.4. При резонансная частота меньше собственной, следовательно, при резонансе <π/2. При малом затухании и .}

_{Рассмотрим зависимость энергии W осциллятора, совершающего установившиеся колебания, от времени. Энергия равна сумме кинетической и потенциальной энергий:}

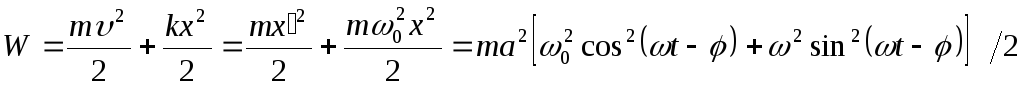_{. График зависимости представлен на рис.1.4. 5. Колебания энергии будут тем меньше, чем ближе частота к , и при = энергия не будет зависеть от времени:}

_{В установившихся колебаниях при работа вынуждающей силы за период будет компенсировать потери энергии с системе за счет работы сил сопротивления. Мощность же вынуждающей силы в каждый момент времени будет равна модулю мощности сил сопротивления только в случае =. В противном случае эти мощности будут равны по модулю только в среднем за период.}

_{Лекция 4}