Контрольные задания
а) Найти общее решение дифференциального уравнения.
б)Найти решение задачи Коши.
в) Найти общее решение дифференциального уравнения.
7.1
а)
;
б)
;
в)
;
7.2
а)
;
б)
;
;
в)
;
7.3
а)
;
б)
;
;
в)
;
7.4
а)
;
б)
;
;
в)
;
7.5
а)
;
б)
;
;
в)
;
7.6
а)
;
б)
;
;
в)
;
7.7
а)
;
б)
;
;
в)
;
7.8
а)
;
б)
;
;
в)
;
7.9
а)
;
б)
;
;
в)
;
7.10
а)
;
б)
;
;
в)
;
7.11
а)
;
б)
;
;
в)
;
7.12
а)
;
б)
;
;
в)
;
7.13
а)
;
б)
;
;
в)
;
7.14
а)
;
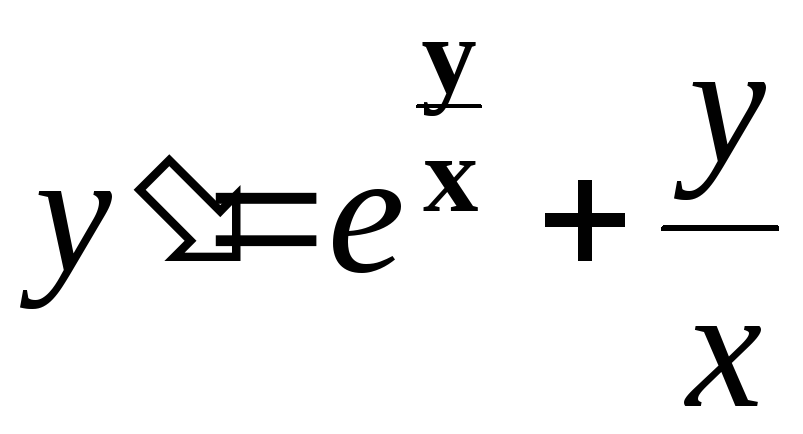б)
;
;
в)
;
7.15
а)
;
б)
;
;
в)
;
7.16
а)
;
б)
;
;
в)
;
7.17
а)
;
б)
;
;
в)
;
7.18
а)
;
б)
;
;
в)
;
7.19
а)
;
б)
;
;
в)
;
7.20
а)
;
б)
;
;
в)
;
Указания к заданию 8
Тема 8. Ряды
Рассмотрим выражение вида
,(1)
называемое
бесконечным рядом, где
—
члены ряда.
Ряд называется числовым, если членами ряда являются числа, ифункциональным, если членами ряда являются функции.
Сумма конечного числа первых n членов называется
n –ой частичной суммой ряда:
Если
существует конечный предел
,
то его называютсуммой
ряда и ряд
называется сходящимся.
Если предел не существует, то ряд
расходится
и суммы не имеет.
Отметим следующие свойства рядов.
1. На сходимости ряда не сказывается отбрасывание конечного числа его членов.
2. Сходимость ряда не нарушится, если все члены умножить на одно и то же ненулевое число.
3. Сумма (разность) сходящихся рядов есть ряд сходящийся.
Необходимый признак сходимости рядов
Если ряд сходится, то предел n-ого члена равен нулю при неограниченном возрастании n, т.е.
.
(2)
Условие
(2) является необходимым, но не достаточным
условием сходимости, поэтому если
,
то ряд может как сходиться, так и
расходиться.
Однако,
если
,
то ряд расходится.
Пример
1. Исследовать
сходимость ряда
.
Решение. Рассмотрим предел общего члена ряда un:
,
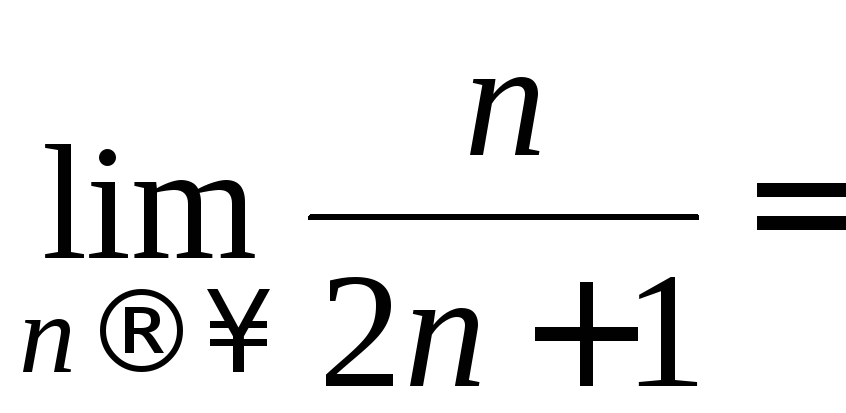
поэтому ряд расходится.
Пример
2. Исследовать
сходимость ряда
.
Решение.
.
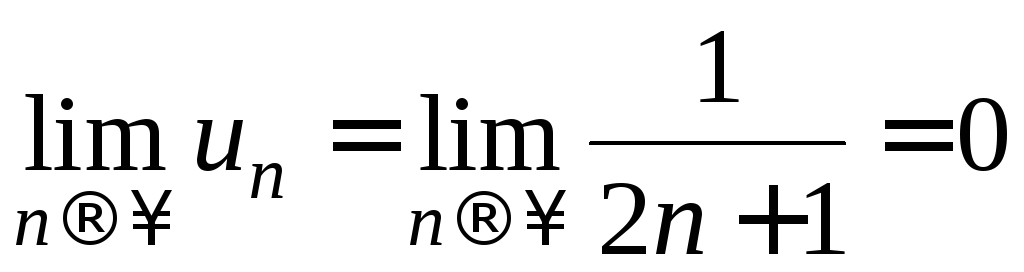Необходимый признак не дает ответа на
вопрос о сходимости данного ряда.
Сформулируем достаточные признаки сходимости некоторых рядов и вернемся к решению примера.
В первую очередь рассмотрим числовые ряды.
Числовые ряды
Знакоположительные ряды
Рассмотрим два ряда с положительными членами:
,
(3)
,
(4)
называемых знакоположительными.
Для них справедливы следующие признаки сходимости.
Признаки сравнения
Признак
1.
Если, начиная
с некоторого n,
выполняется условие
и ряд (4) сходится, то ряд (3) тоже сходится.
Признак
2.
Если, начиная с некоторого n,
выполняется условие
,
и ряд (4) расходится, то ряд (3) тоже
расходится.
Признак
3.
Если существует конечный и отличный от
нуля предел
,
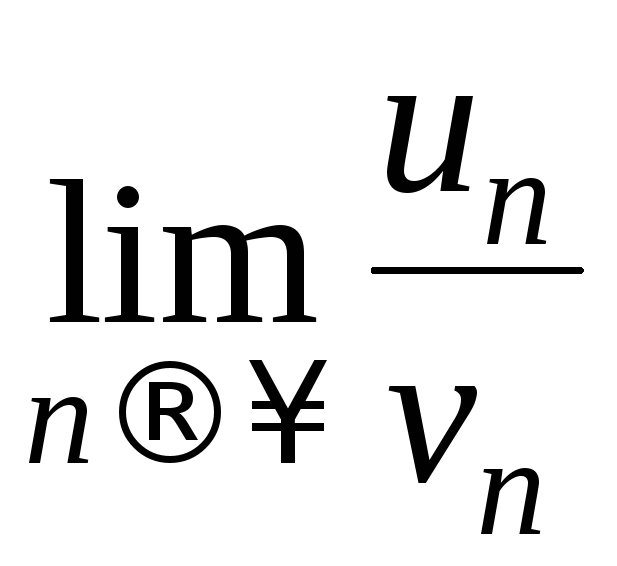то ряды (3) и (4) ведут себя одинаково, т.е.
сходятся и расходятся одновременно.
При использовании этих признаков нужно сравнивать исследуемый ряд с рядом, сходимость или расходимость которого уже известна.
Для сравнения обычно выбирают один из следующих рядов:
I.
—
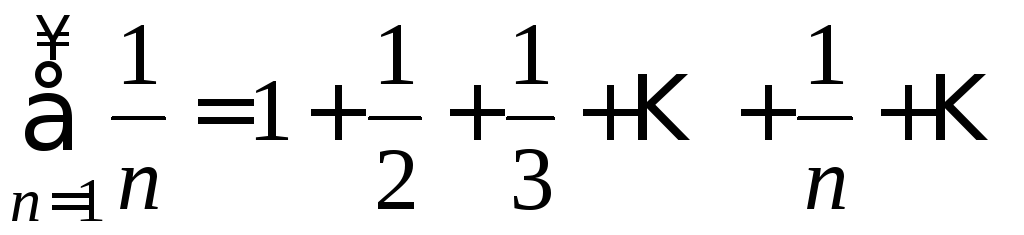гармонический ряд, он расходится.
II.
(
)
— геометрическая прогрессия, при
ряд сходится, при
1
расходится.
III.
— ряд Дирихле (обобщенный гармонический
ряд), при
сходится, при
1
расходится.
Пример
3. Вернемся
к ряду из примера 2:
.
Решение.
Это ряд с положительными членами. Сравним
исходный ряд
с гармоническим рядом
.
Рассмотрим предел отношения общих
членов рядов:
.
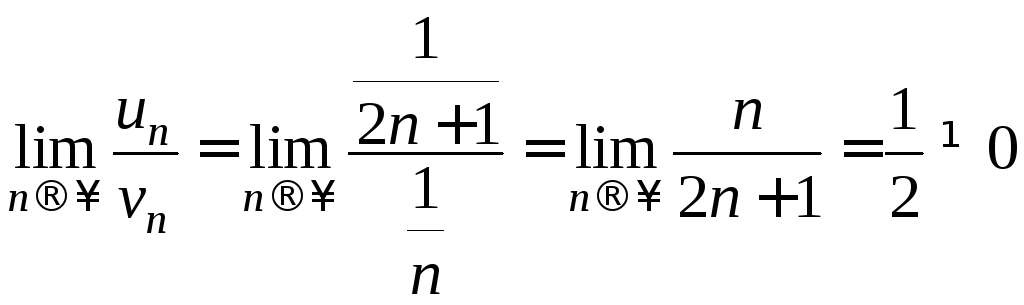Ряд (2) расходится, следовательно, на основании признака 3 исходный ряд также расходится.
Пример
4. Исследовать
сходимость ряда
.
Решение.
В качестве
сравнения возьмем геометрическую
прогрессию
,
которая сходится, т.к.
=
1.
Сравнимобщие
члены рядов:
.
На основании первого признака сравнения
исходный ряд сходится.
Пример
5. Исследовать
сходимость ряда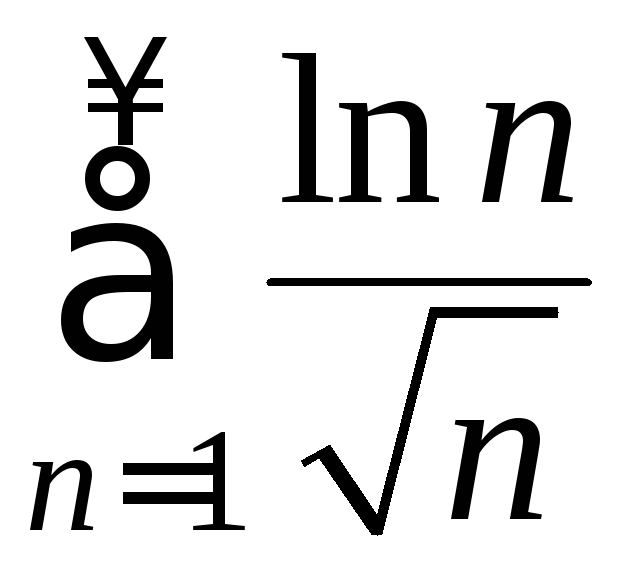
.
Решение.
Рассмотрим
расходящийся ряд
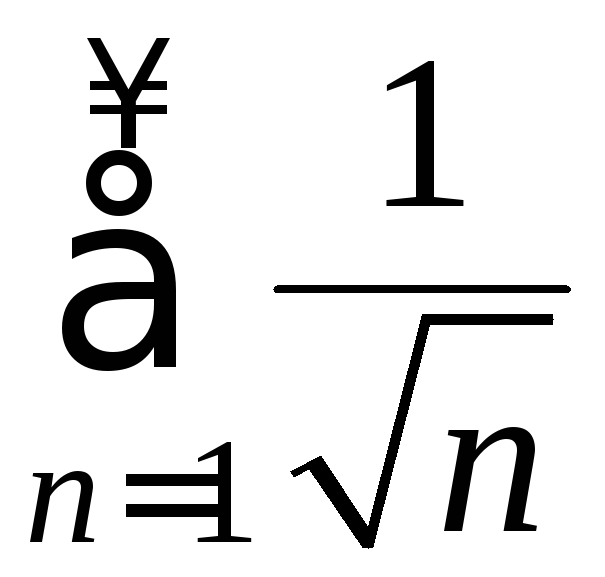(ряд Дирихле). Поскольку, начиная с
,
выполняется условие
,
то, согласно второму признаку сравнения,
исходный ряд расходится.
Признак Даламбера
Если
в знакоположительном ряде 
существует предел
,
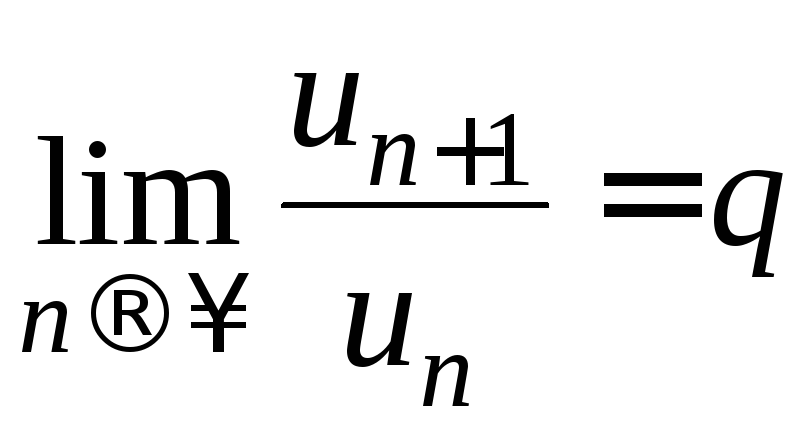то приq
1
ряд сходится, приq
1
расходится, при
q=1 признак
Даламбера ответа на вопрос о сходимости
ряда не дает и надо использовать другие
признаки.
Пример
6.
Исследовать
сходимость ряда
.
Решение.
Поскольку
,
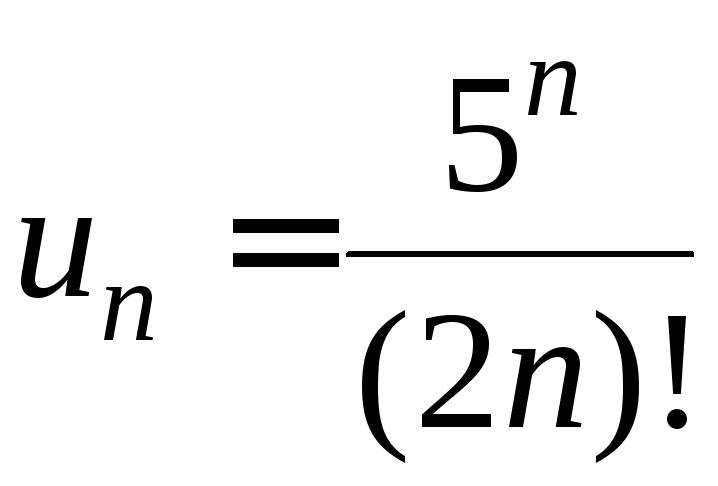то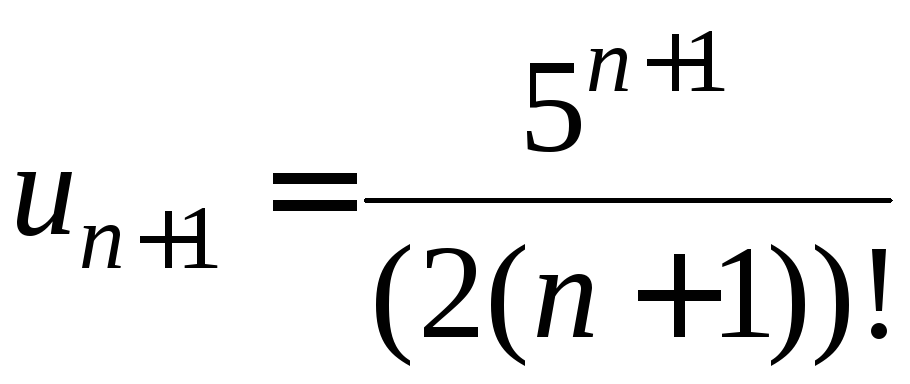
.
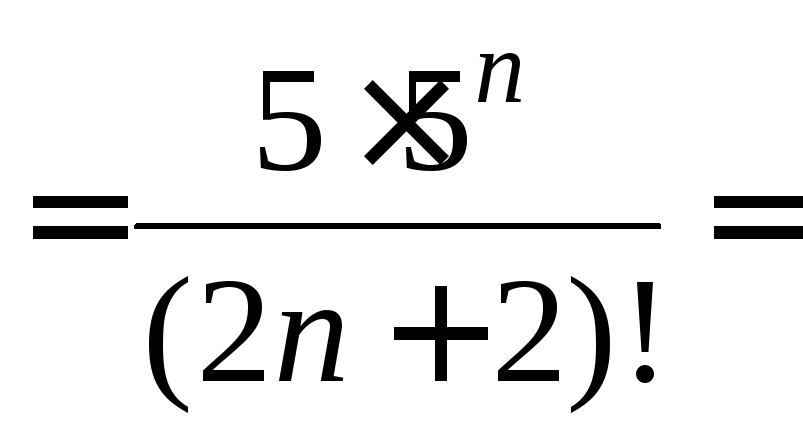
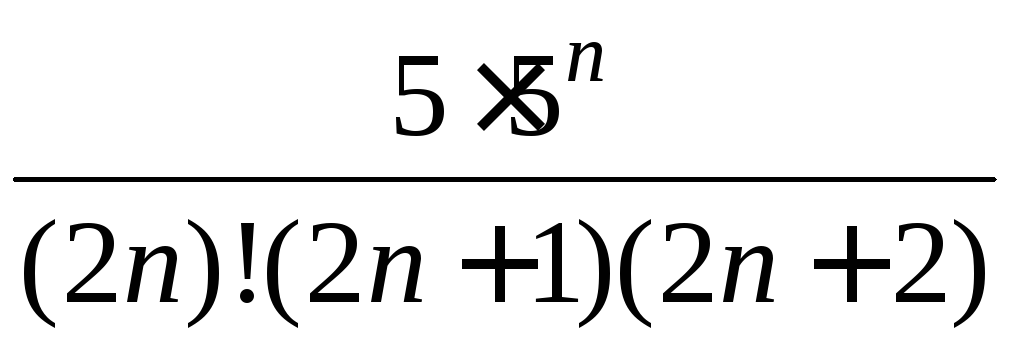(Напомним, чтоn!=
).
Теперь найдем предел отношения
:
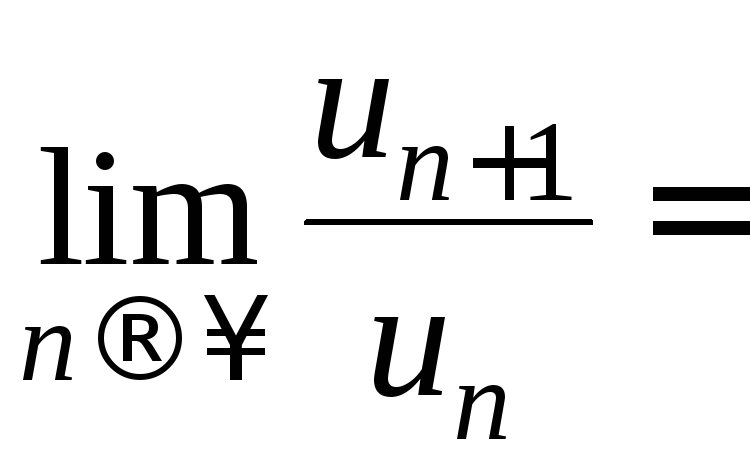
Так
как 0<1, то по признаку Даламбера исходный
ряд сходится.
Радикальный признак Коши
Если
в знакоположительном ряде 
существует предел
,
то приq<1
ряд сходится, при q
1
расходится, при
q=1 вопрос о
сходимости ряда остается открытым.
Пример
7. Исследовать
сходимость ряда
.
Решение. Поскольку общий член ряда содержит n-ую степень, применим радикальный признак Коши.
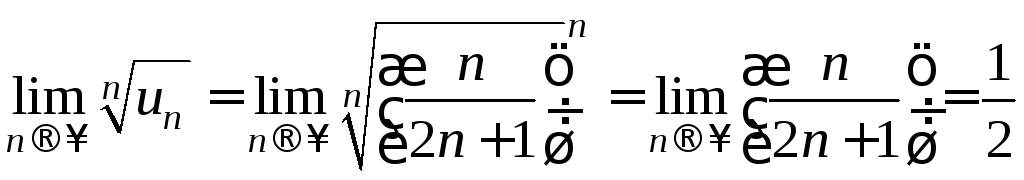
1,
следовательно, ряд сходится.
Интегральный признак Коши
Если
,
где функция
положительна,
монотонно убывает и непрерывна при
,
то ряд
и интеграл
сходятся или расходятся одновременно.
Пример
8. Исследовать
сходимость ряда
.
Решение.
Рассмотрим
функцию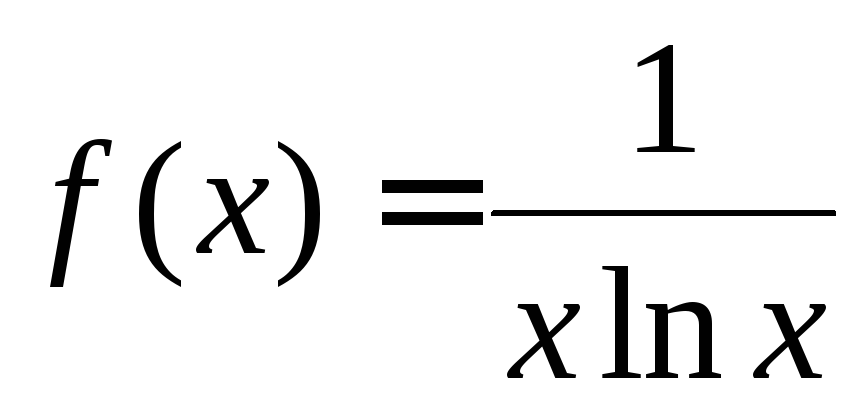
.
При
функция
положительна,
монотонно убывает и непрерывна, т.е.
удовлетворяет условию интегрального
признака Коши. Рассмотрим интеграл
.
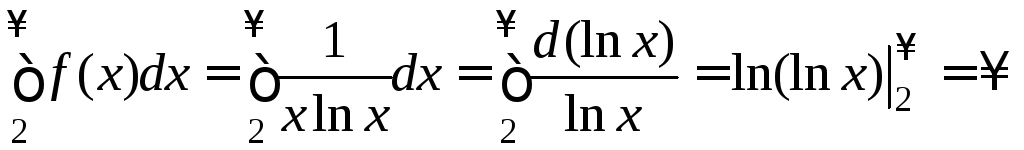Из расходимости интеграла следует расходимость исходного ряда.
Знакочередующиеся ряды
Ряд
(5)
называется знакопеременным, если среди его членов есть как положительные, так и отрицательные.
Составим ряд из абсолютных значений ряда (5):
(6)
Если ряд (6) сходится, то ряд (5) тоже сходится и называется абсолютно сходящимся.
Из расходимости ряда (6) не следует расходимость ряда (5).
Если ряд (6) расходится, а ряд (5) сходится, то он называется сходящимся условно.
Ряд (6) является знакоположительным рядом и вопрос о его сходимости решается с помощью признаков, рассмотренных ранее.
Частным случаем знакопеременного ряда является знакочередующийся ряд.
Знакочередующимся называется ряд
,
(7)
где
для
.
Для решения вопроса о сходимости знакочередующегося ряда используют признак сходимости Лейбница.
Признак сходимости Лейбница
Если для знакочередующегося ряда (7) выполнены условия:
1.
(начиная с некоторогоn),
2.
,
то ряд (7) сходится.
Пример
9. Исследовать
сходимость ряда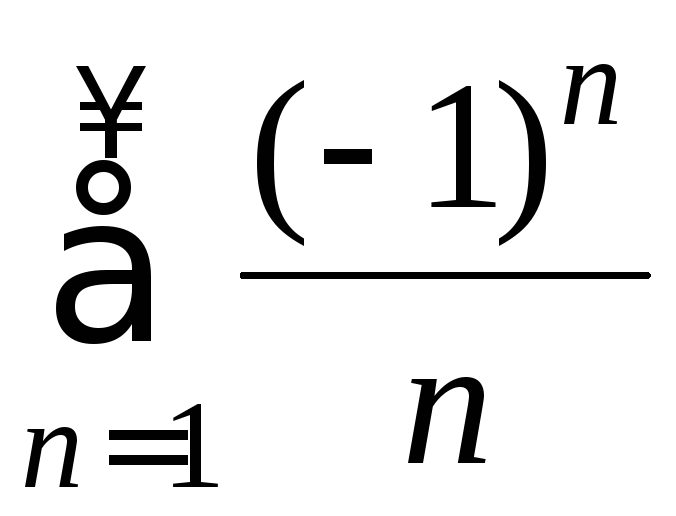
.
Решение.
Это
знакочередующийся ряд, для которого
выполнены условия признака сходимости
Лейбница:
,
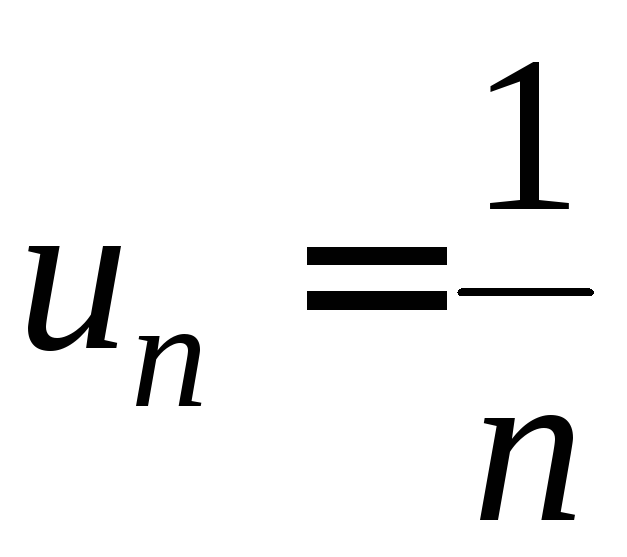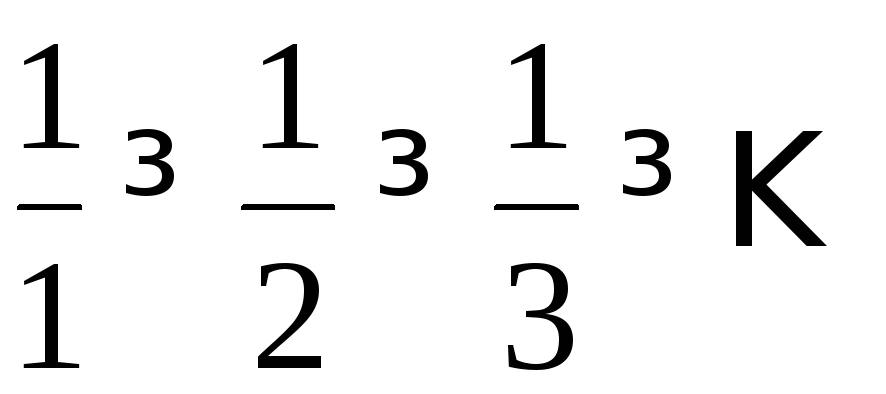и
,
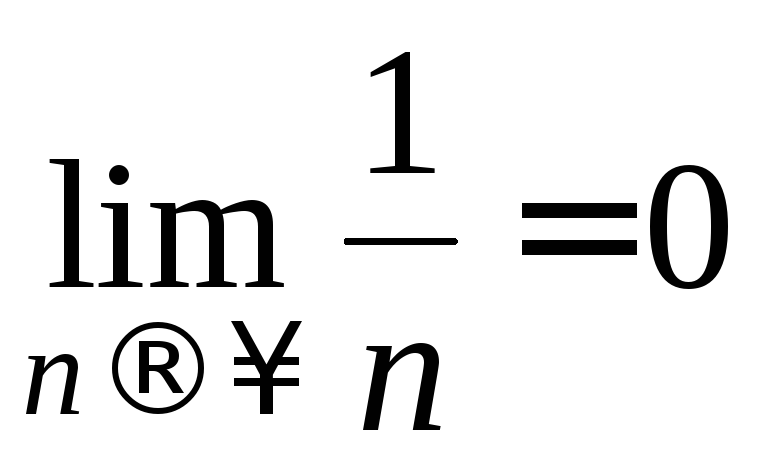поэтому ряд сходится. Он сходится
условно, т.к. ряд, составленный из
абсолютных значений, является гармоническим
,
который расходится.
Пример
10. Исследовать
сходимость ряда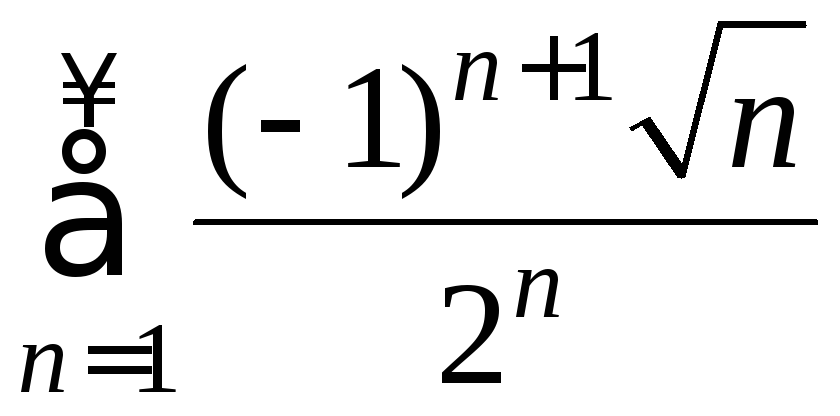
.
Решение.
Рассмотрим
ряд, составленный из абсолютных значений
.
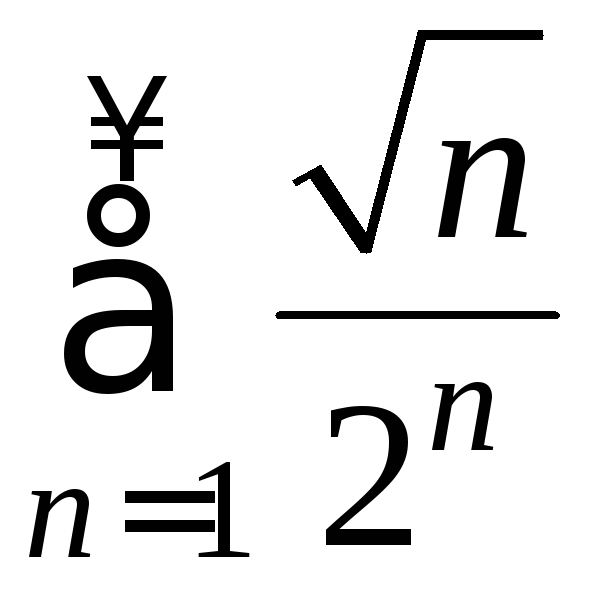Применим к нему признак сходимости
Даламбера:
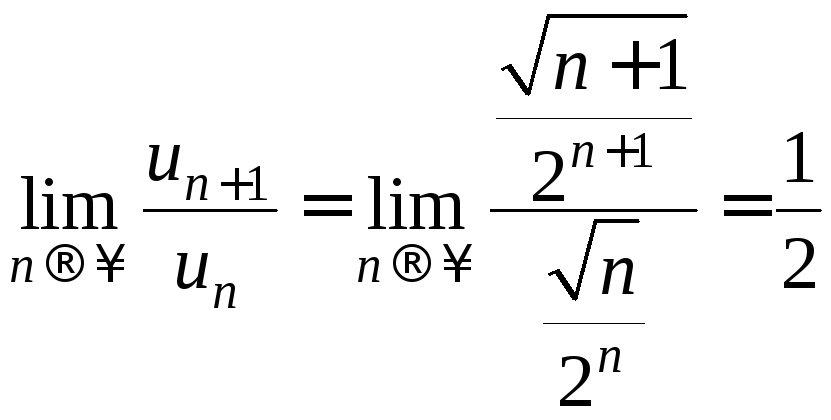
1,
следовательно, этот ряд сходится, поэтому
исходный ряд сходится абсолютно.
Пример
11. Исследовать
сходимость ряда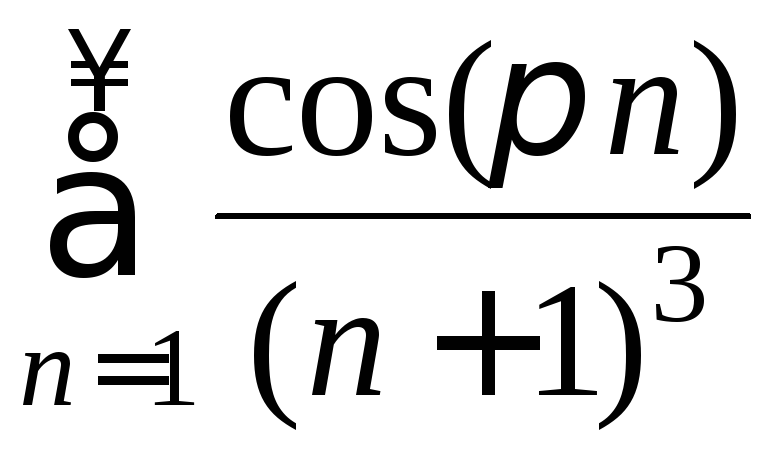
.
Решение.
Это
знакочередующийся ряд. Составленный
из абсолютных значений ряд имеет вид
.
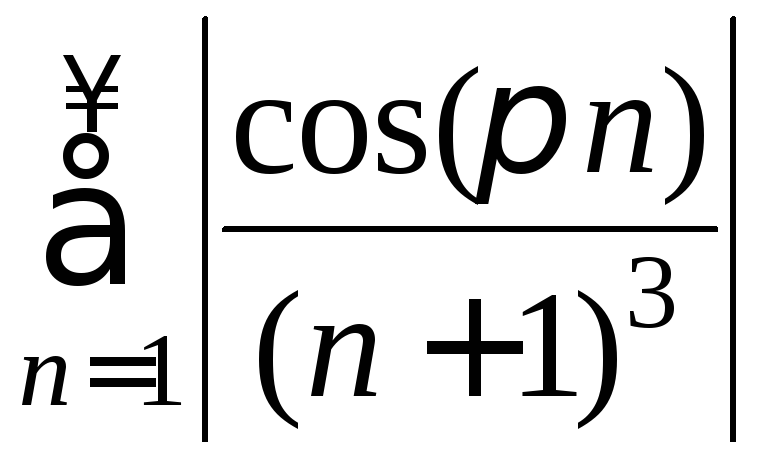Сравним члены этого ряда с членами
сходящегося ряда Дирихле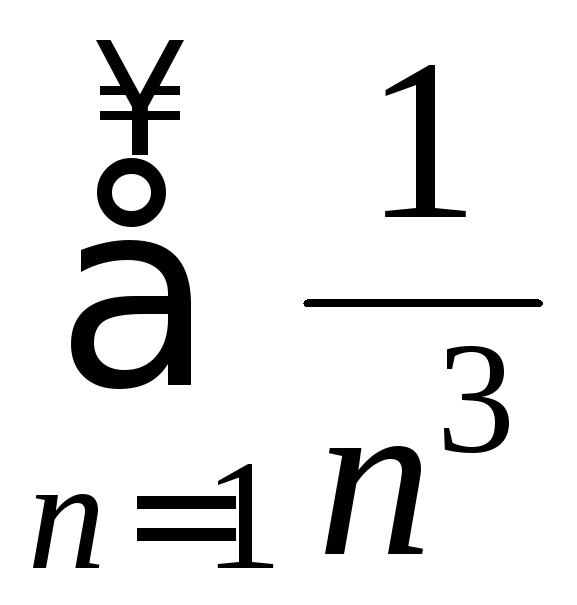
:
.
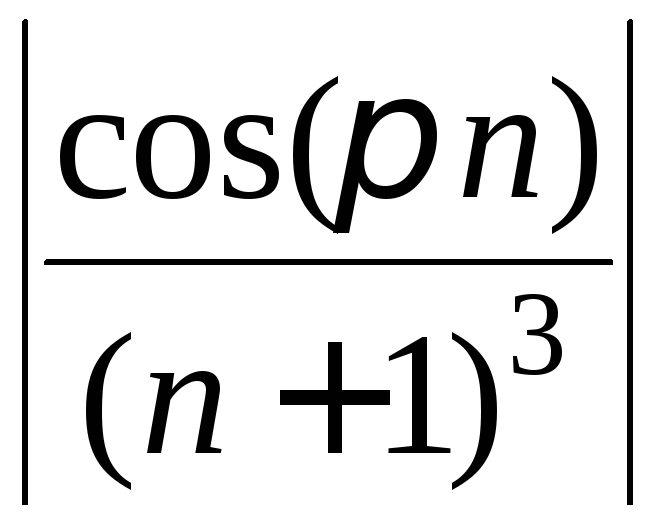
Согласно первому признаку сравнения,
ряд
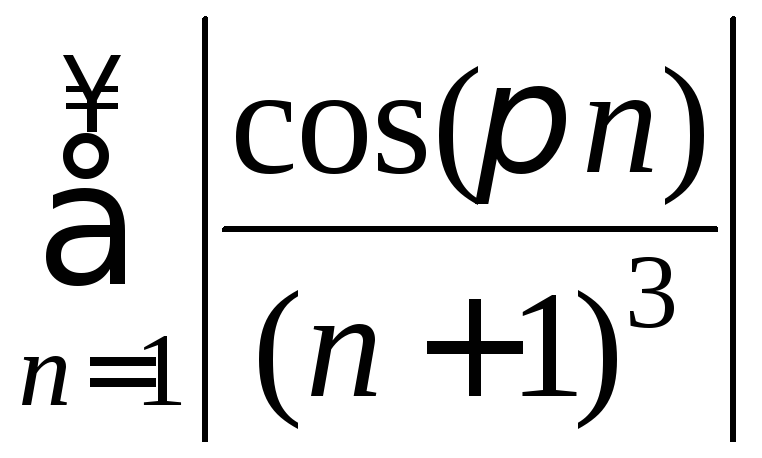сходится, поэтому исходный ряд сходится
абсолютно.
Функциональные ряды
Функциональным
называется
ряд
,членами
которого являются зависящие от
функции. Множество значений аргумента
,
при которых ряд сходится, называется
областью
сходимости ряда.
Частным
случаем функционального ряда является
степенной
ряд:
,
(8) где
и
—
вещественные числа.
Для
ряда (8) существует такой интервал
(называемый интервалом сходимости)
с центром в точке
,
внутри которого ряд (8) сходится абсолютно,
а при
>
ряд расходится. Число
называютрадиусом
сходимости
степенного ряда. Радиус
сходимости R
в частном случае может быть равен 0 или
.
На концах интервала сходимости степенной
ряд может как сходиться, так и расходиться.
Для
выяснения вопроса о сходимости ряда на
концах интервала сходимости достаточно
применить к ряду известные признаки
сходимости, считая
фиксированным и равным
.
Пример
12. Найти
область сходимости ряда
.
Решение. Применим к ряду признак сходимости Даламбера и рассмотрим предел:
.
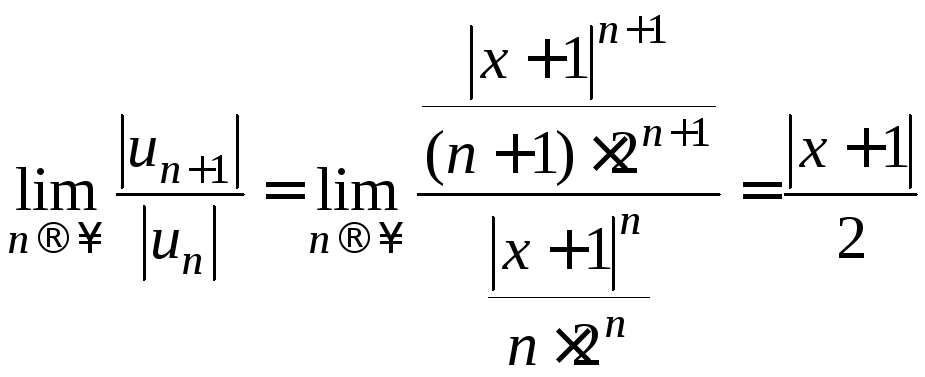Если
,
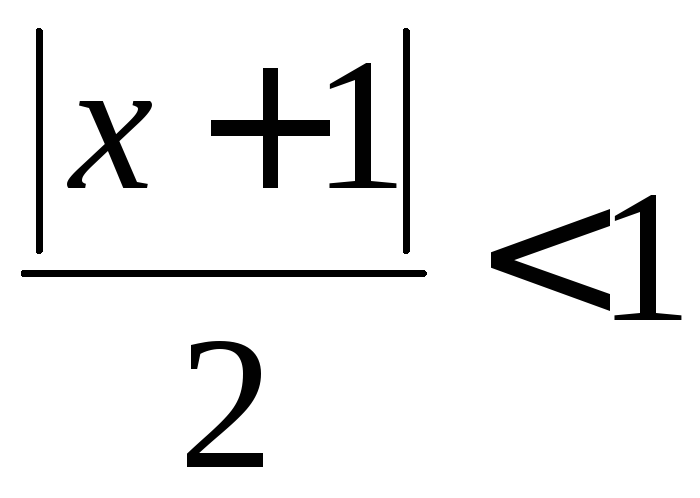то исходный ряд сходится абсолютно,
т.е. при
2
или на интервале
.
Если
,
то ряд расходится, т.е. при
.
Проверим сходимость на концах интервала сходимости.
При
получаем числовой ряд:
.
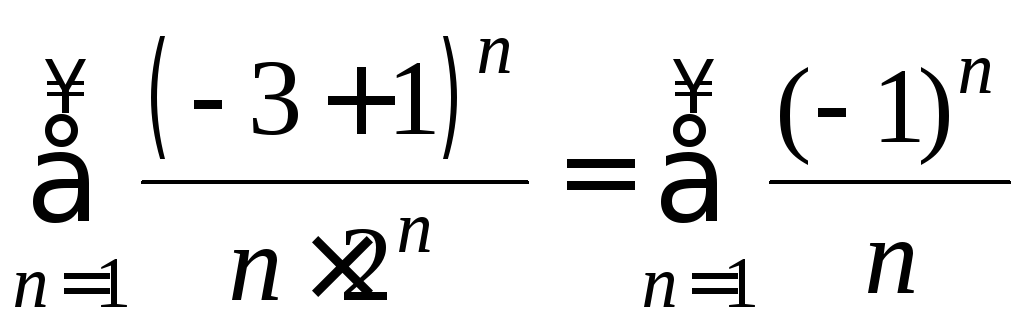Это знакочередующийся ряд, который сходится по признаку Лейбница неабсолютно (см. пример 9).
При
получаем гармонический ряд:
,
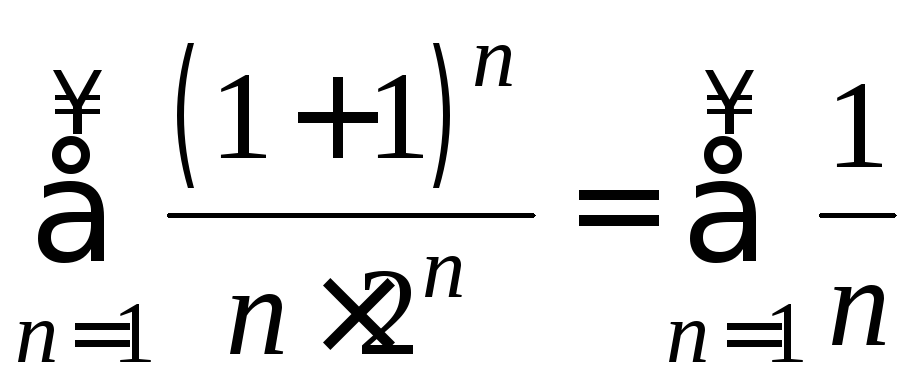который расходится.
Окончательный
ответ: ряд сходится при
.
Пример 13. Определить область сходимости ряда:
.
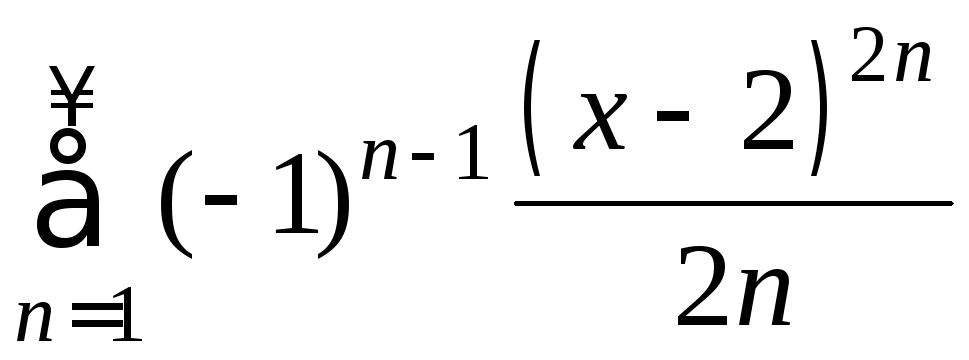Решение. Применим к ряду признак сходимости Даламбера и рассмотрим предел:
.
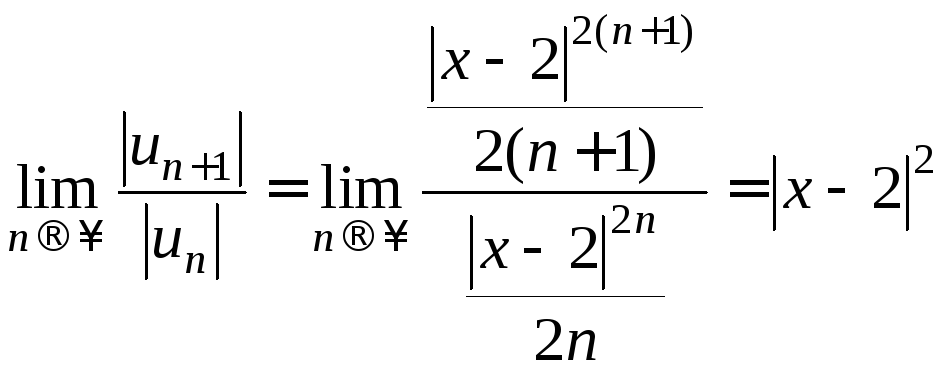Исходный
ряд сходится абсолютно, если
,
то есть при
.
Ряд расходится, если
,
то есть при
.
Рассмотрим поведение ряда на концах интервала сходимости.
При
получаем числовой ряд:
.
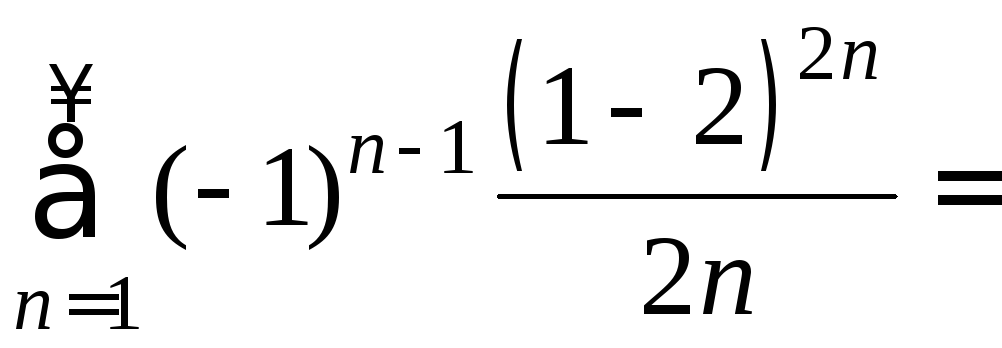
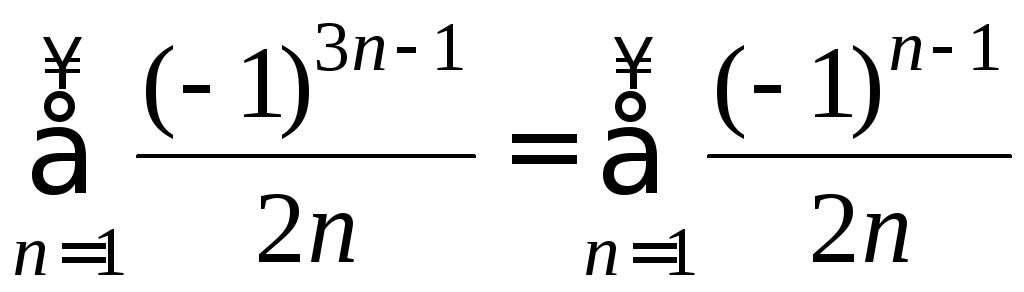Это
знакочередующийся ряд, для которого
выполнены условия признака сходимости
Лейбница:
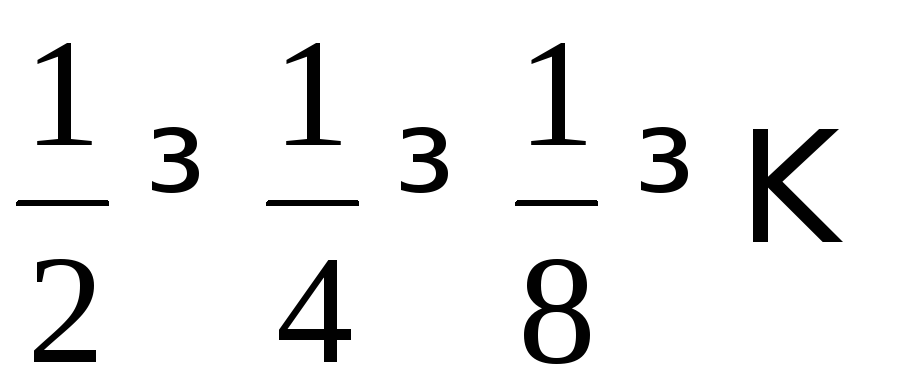и
.
Поэтому ряд сходится (сходится условно,
т.к. ряд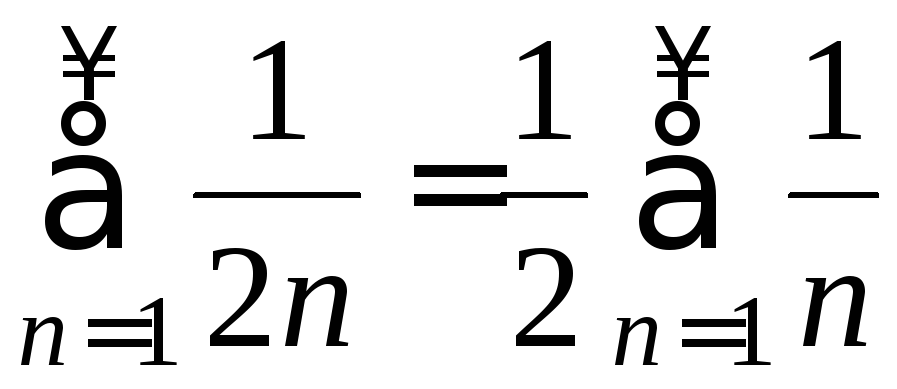
расходится, а умножение всех членов
ряда на постоянное число, отличное от
нуля, не меняет его сходимости).
При
получаем такой же сходящийся ряд:
.
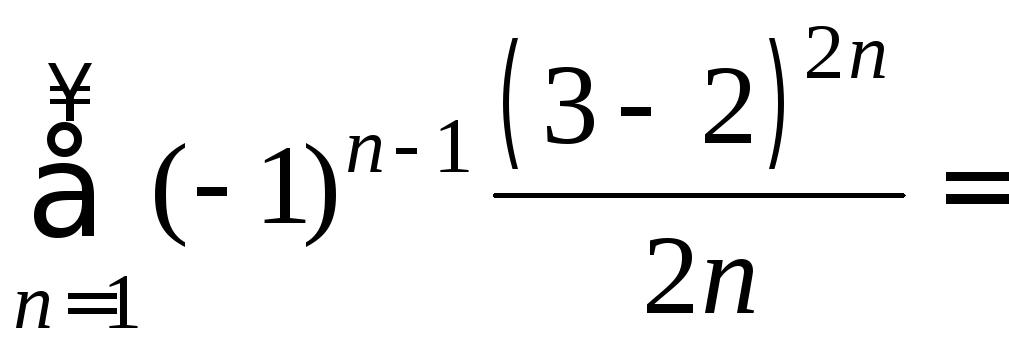
Окончательный
ответ: ряд сходится при
.
Пример
14. Определить
область сходимости ряда
.
Решение. Рассмотрим предел:
.
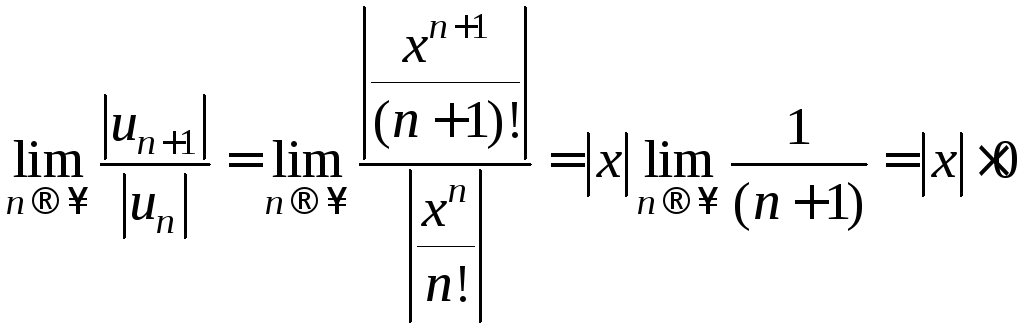Неравенство
выполняется при всех значениях
,
поэтому область сходимости ряда
.