
- •Математика
- •Содержание
- •1. Общие положения
- •2. Методические указания к изучению дисциплины
- •3. Методические указания к выполнению контрольной работы
- •Контрольная работа №2 Указания к заданию 1
- •Тема 1. Предел функции
- •Контрольные задания
- •Указания к заданию 2
- •Тема 2. Основы дифференциального исчисления
- •Контрольные задания
- •Указания к заданию 3
- •Тема 3. Исследование функции и построение графика
- •Контрольные задания
- •Указания к заданию 4
- •Тема 4. Функции двух переменных
- •Контрольные задания
- •Указания к заданию 5 тема 5. Неопределенный интеграл
- •Свойства неопределенного интеграла
- •Основные методы интегрирования Непосредственное интегрирование
- •Замена переменой в неопределенном интеграле
- •Интегрирование по частям в неопределенном интеграле
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрических функций
- •Интегрирование некоторых иррациональных функций
- •Контрольные задания
- •Указания к заданию 6 тема 6. Определенный интеграл
- •Свойства определенного интеграла
- •Объем тела вращения
- •Контрольные задания
- •Указания к заданию 7
- •Тема 7. Дифференциальные уравнения
- •Уравнение с разделяющимися переменными
- •Однородное уравнение первого порядка
- •Линейное уравнение первого порядка
- •Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами
- •Контрольные задания
- •Указания к заданию 8
- •Тема 8. Ряды
- •Рассмотрим выражение вида
- •Контрольные задания
- •5. Требования к выполнению контрольной работы
- •6. Список литературы
- •Содержание дисциплины
- •Раздел 1. Основы алгебры и анализа
- •Тема 1.3. Введение в анализ функций одной переменной.
- •Тема 1.4. Дифференциальное исчисление функции одной переменной.
- •Раздел 2. Функции нескольких переменных. Интегральное исчисление.
- •Тема 2.1. Функции нескольких переменных.
- •Тема 2.2. Неопределенный интеграл.
- •Тема 2.3. Определенный интеграл.
- •Раздел 3. Обыкновенные дифференциальные уравнения. Ряды.
- •Тема 3.1. Обыкновенные дифференциальные уравнения (оду).
- •Тема 3.2. Системы обыкновенных дифференциальных уравнений.
- •Тема 3.3. Числовые ряды.
- •Тема 3.4. Функциональные ряды.
- •Образец оформления титульного листа
Контрольные задания
Исследовать функцию методами дифференциального исчисления и построить ее график.
3.1.![]() .
3.2.
.
3.2.
![]()
3.3.![]() 3.4.
3.4.
![]()
3.5.![]() 3.6.
3.6.
![]()
3.7.![]() 3.8.
3.8.
![]()
3.9.![]() 3.10.
3.10.![]()
3.11.![]() 3.12.
3.12.![]()
3.13.![]() 3.14.
3.14.![]()
3.15.
![]() 3.16.
3.16.
![]() .
.
3.17.![]() .
3.18.
.
3.18.
![]()
3.19.
![]() 3.20.
3.20.![]()
Указания к заданию 4
Тема 4. Функции двух переменных
Рассмотрим
функцию двух переменных
![]() ,
определенную в некоторой области
,
определенную в некоторой области![]() ,
являющейся частью плоскости
,
являющейся частью плоскости![]() Частной
производной от функции
Частной
производной от функции
![]() по независимой переменной х
называется производная
по независимой переменной х
называется производная
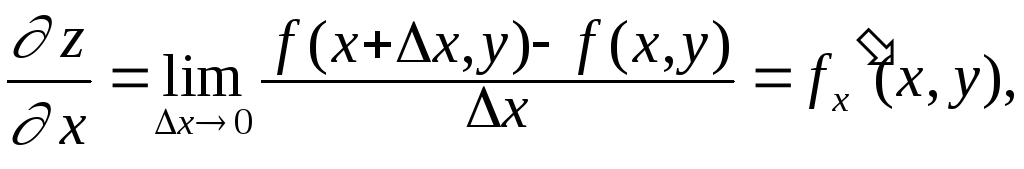
вычисленная при постоянном у.
Частной производной по у называется производная
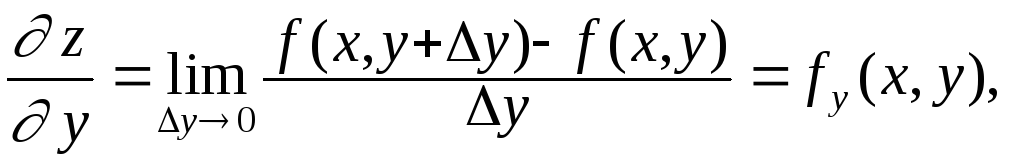
вычисленная при постоянном х.
Для частных производных справедливы обычные правила и формулы дифференцирования.
При
изменении
![]() и
и![]() частные производные сами являются
функциями, и можно вычислять частные
производные от этих функций. Частные
производные второго порядка обозначают
следующим образом:
частные производные сами являются
функциями, и можно вычислять частные
производные от этих функций. Частные
производные второго порядка обозначают
следующим образом:
![]()
Последнюю
из трех частных производных второго
порядка называют смешанной
производной.
Если частные производные второго
порядка непрерывны в точке
![]() ,
тогда
,
тогда![]() ,
то есть не важно, в какой последовательности
вычисляется смешанная производная.
,
то есть не важно, в какой последовательности
вычисляется смешанная производная.
Градиентом
функции
![]() в точке
в точке
![]() называется вектор, составленный из
частных производных:
называется вектор, составленный из
частных производных:
![]()
Этот
вектор указывает в точке М0
направление наискорейшего роста функции
![]() .
.
Для
функции двух переменных вводится понятие
производной по направлению, аналогичное
понятию частной производной, когда
приращение аргумента задается вдоль
данного направления. Для любого
направления, задаваемого вектором
![]() ,
производная функции
,
производная функции![]() в точке
в точке![]() по направлению
этого вектора может быть выражена
следующим образом:
по направлению
этого вектора может быть выражена
следующим образом:
![]()
где
знак модуля
означает длину вектора градиента в
точке
![]() ,
а
,
а
![]() ─
угол между градиентом и направлением
─
угол между градиентом и направлением
![]() .
.
Пример.
Найти градиент функции
![]() в
точке
в
точке![]() .
.
Решение. Рассматривая у как постоянную величину, дифференцируем функцию по переменной х.
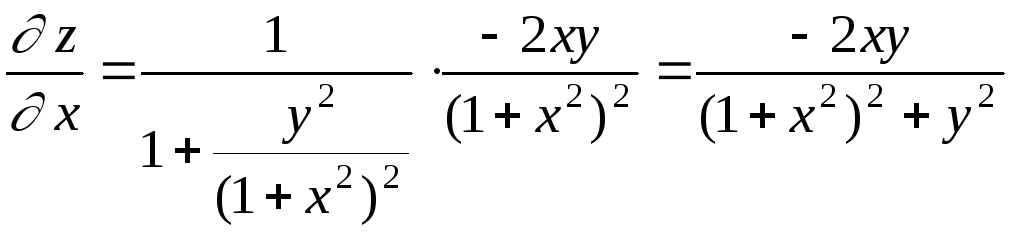 .
.
Аналогично, рассматривая х как постоянную величину, получаем:
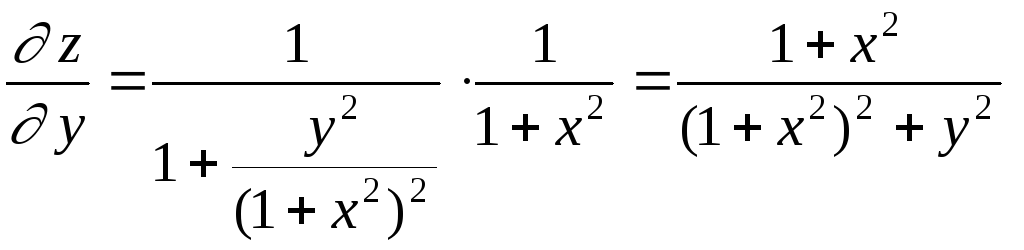 .
.
Находим
значения частных производных в точке
![]() :
:
![]() ,
,
![]()
Таким
образом,
![]()
Контрольные задания
Найти
![]()
![]() градиент
функции Z
в точке М.
градиент
функции Z
в точке М.
4.1
![]() .
.
4.2
![]()
4.3
![]()
4.4
![]()
4.5
![]()
4.6
![]()
4.7
![]()
4.8![]()
4.9
![]()
4.10
![]()
4.11
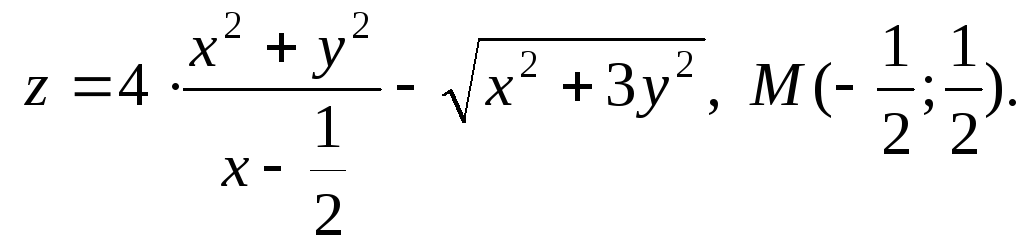
4.12
![]()
4.13
![]()
4.14
![]()
4.15
![]()
4.16
![]()
4.17
![]()
4.18
![]()
4.19
![]()
4![]()
![]()
![]()
![]()
![]()
![]()
![]() .20
.20
![]()
![]()
![]()
![]()
Указания к заданию 5 тема 5. Неопределенный интеграл
Функция
![]() называетсяпервообразной для функции
называетсяпервообразной для функции![]() на некотором промежутке, если для всех
значений
на некотором промежутке, если для всех
значений![]() из этого промежутка выполняется равенство
из этого промежутка выполняется равенство![]() .
.
Например, функция
![]() является первообразной для функции
является первообразной для функции![]() ,
так как при любом
,
так как при любом![]()
![]() .
.
Можно заметить, что первообразной для![]() является не только,
является не только,![]() но и функция
но и функция![]() + С, где С ─ любая постоянная. Это
справедливо для любой функции
+ С, где С ─ любая постоянная. Это
справедливо для любой функции![]() ,
имеющей первообразную.
,
имеющей первообразную.
Теорема.Пусть![]() является первообразной для функции
является первообразной для функции![]() в некотором интервале
в некотором интервале![]() ;
тогда функция
;
тогда функция![]() , где С ─ любая постоянная, также будет
первообразной для
, где С ─ любая постоянная, также будет
первообразной для![]() .
.
Из теоремы следует, что любые две первообразные для одной и той же функции могут отличаться друг от друга только на постоянное слагаемое.
Если
![]() ─
первообразная для функции
─
первообразная для функции![]() ,
то совокупность всех первообразных
,
то совокупность всех первообразных![]() ,
где С ─ произвольная постоянная,
называетсянеопределенным интеграломот функции
,
где С ─ произвольная постоянная,
называетсянеопределенным интеграломот функции![]() и обозначается символом
и обозначается символом![]() .
Таким образом,
.
Таким образом,![]() =
=![]() .
.
Функция
![]() называется подынтегральной функцией,
произведение
называется подынтегральной функцией,
произведение![]() ─ подынтегральным выражением, переменная
─ подынтегральным выражением, переменная![]() -
переменной интегрирования, а символ
-
переменной интегрирования, а символ![]() -
знаком интеграла.
-
знаком интеграла.
Операция нахождения неопределенного
интеграла от данной функции называется
интегрированиемфункции![]() .Операция интегрирования является
обратной к операции дифференцирования.
.Операция интегрирования является
обратной к операции дифференцирования.
