Уравнение с разделяющимися переменными

Дифференциальным уравнением с разделяющимися переменными называется уравнение вида:

Для его решения следует сначала разделить переменные, то есть разнести их в разные стороны уравнения:

(),

а затем проинтегрировать обе части уравнения:

.

Следует иметь в виду, что полученные неопределенные интегралы могут различаться на произвольную постоянную .

Пример1. Решить задачу Коши: ,.

Решение. Поделим обе части уравнения на

Тогда и.

Вычисляя интегралы, находим: .

Отсюда общее решение.

Подставим в это решение начальное условие: ; Следовательно,иискомое частное решение, то есть решение задачи Коши.

Однородное уравнение первого порядка

Однородным уравнением первого порядка называется уравнение вида:

. (6)

Для его решения введем новую переменную . Тогдаи. Подставляя эти соотношения в (6), получаем:или. Это уравнение с разделяющимися переменными, и оно легко интегрируется. Найдя, получаем искомое решение.

Пример2. Решить уравнение: .

Решение. Полагая и, получим:

, или .

Интегрируя обе части последнего уравнения, получим:

.

Произвольная постоянная здесь взята в виде для удобства. Тогдаи окончательно общее решение принимает вид:

.

Пример3. Решить уравнение: .

Решение. Пусть . Тогда разделим обе части уравнения на:

.

После замены переменной это уравнение приводится к виду:

, или .

Вычислим интеграл в левой части последнего уравнения:

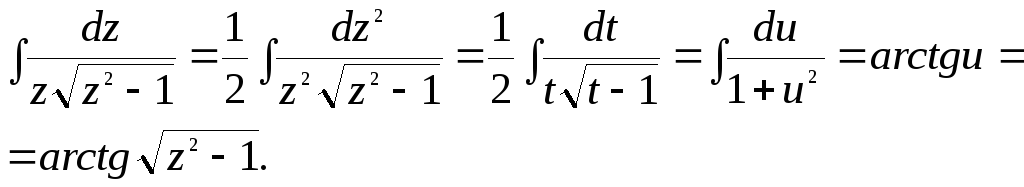
Тогда , и общее решение уравнения записывается в следующем виде:

.

Линейное уравнение первого порядка

Решить линейное дифференциальное уравнение первого порядка можно с помощью введения двух новых искомых функций и, положив, и дополнительного условия на одну из них, выби­раемую произвольно. Рассмотрим применение этого метода на следующем примере.

Пример4. Решить дифференциальное уравнение .

Решение. Будем искать решение в виде: ;

Тогда ; Подставляя выражения для искомой функции и ее производной в рассматриваемое дифференциальное уравнение, получим:

, или

. (7)

Поскольку одну из функций имы вправе выбрать произвольно, выберем ее так, чтобы выполнялось условие:Тогда уравнение (7) запишется в виде:. Это уравнение легко интегрируется:;.

Произвольную постоянную здесь можно положить равной нулю, так как мы выбираем частное решение. Тогда .

После подстановки в исходное уравнение получим (при):

; ;.

Таким образом, искомое общее решение.

Уравнение Бернулли

Уравнением Бернулли называется уравнение следующего вида:

. (8)

Здесь и, так как в этих случаях уравнение (8) превращается в линейное уравнение.

Уравнение Бернулли, как и линейное уравнение, решается с помощью представления этой функции в виде .

Пример5. Решить уравнение:

. (9)

Решение. Это уравнение Бернулли и . Положим. Тогда уравнение (9) запишется в виде:

. (10)

Будем искать функцию как решение уравнения:

.

Тогда и. Вычисляя интегралы, получим:

и

Подставляя полученное выражение в (10), получим:

.

Разделяя переменные и интегрируя, получим:

.

Выполняя интегрирование, приходим к выражению:

, или .

Окончательно получаем: .

Дифференциальные уравнения второго порядка

Дифференциальное уравнение второго порядка имеет вид:

. (11)

Если уравнение (11) может быть разрешено относительно второй производной, то оно записывается в следующей форме:

.

Задача Коши для дифференциального уравнения второго порядка состоит в нахождении частного решения, удовлетворяющего начальным условиям:

Линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами

Дифференциальные уравнения этого типа представляются в виде:

, (12)

где - постоянные числа.

Будем искать решение уравнения (12) в виде , где постоянное число. После подстановки этого выражения в (12) получим:

.

Поскольку , должно выполняться квадратное уравнение:

. (13)

Это уравнение называется характеристическим уравнением для уравнения (12). В зависимости от величины его дискриминанта возможны три случая:

а) .

Можно показать, что общим решением в этом случае является комбинация двух линейно-независимых решений, отвечающих двум различным корням характеристического уравнения:

. (14)

б) .

В этом случае общим решением будет:

. (15)

в) . В этом случае характеристическое уравнение имеет два комплексно-сопряженных корня:и

Общее решение записывается в следующем виде:

. (16)

В формулах (14)–(16) ипроизвольные постоянные.

Пример6. Решить дифференциальное уравнение: ;

Решение. Характеристическое уравнение принимает вид: ; Дискриминант положителен, уравнение имеет два различных корня:. Тогда, согласно (14), общее решение дифференциального уравнения записывается в виде:

.

Пример7. Решить дифференциальное уравнение: ;

Решение. Характеристическое уравнение имеет один кратный корень; В соответствии с (15) общее решение дифференциального уравнения записывается в виде:

.

Пример8. Решить дифференциальное уравнение:

.

Решение. Дискриминант характеристического уравнения отрицателен, характеристическое уравнение имеет комплексные корни: В этом случае формула (16) дает следующее общее решение дифференциального уравнения:

.