
- •Математика
- •Содержание
- •1. Общие положения
- •2. Методические указания к изучению дисциплины
- •3. Методические указания к выполнению контрольной работы
- •Контрольная работа №2 Указания к заданию 1
- •Тема 1. Предел функции
- •Контрольные задания
- •Указания к заданию 2
- •Тема 2. Основы дифференциального исчисления
- •Контрольные задания
- •Указания к заданию 3
- •Тема 3. Исследование функции и построение графика
- •Контрольные задания
- •Указания к заданию 4
- •Тема 4. Функции двух переменных
- •Контрольные задания
- •Указания к заданию 5 тема 5. Неопределенный интеграл
- •Свойства неопределенного интеграла
- •Основные методы интегрирования Непосредственное интегрирование
- •Замена переменой в неопределенном интеграле
- •Интегрирование по частям в неопределенном интеграле
- •Интегрирование рациональных дробей
- •Интегрирование тригонометрических функций
- •Интегрирование некоторых иррациональных функций
- •Контрольные задания
- •Указания к заданию 6 тема 6. Определенный интеграл
- •Свойства определенного интеграла
- •Объем тела вращения
- •Контрольные задания
- •Указания к заданию 7
- •Тема 7. Дифференциальные уравнения
- •Уравнение с разделяющимися переменными
- •Однородное уравнение первого порядка
- •Линейное уравнение первого порядка
- •Линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами
- •Контрольные задания
- •Указания к заданию 8
- •Тема 8. Ряды
- •Рассмотрим выражение вида
- •Контрольные задания
- •5. Требования к выполнению контрольной работы
- •6. Список литературы
- •Содержание дисциплины
- •Раздел 1. Основы алгебры и анализа
- •Тема 1.3. Введение в анализ функций одной переменной.
- •Тема 1.4. Дифференциальное исчисление функции одной переменной.
- •Раздел 2. Функции нескольких переменных. Интегральное исчисление.
- •Тема 2.1. Функции нескольких переменных.
- •Тема 2.2. Неопределенный интеграл.
- •Тема 2.3. Определенный интеграл.
- •Раздел 3. Обыкновенные дифференциальные уравнения. Ряды.
- •Тема 3.1. Обыкновенные дифференциальные уравнения (оду).
- •Тема 3.2. Системы обыкновенных дифференциальных уравнений.
- •Тема 3.3. Числовые ряды.
- •Тема 3.4. Функциональные ряды.
- •Образец оформления титульного листа
Интегрирование тригонометрических функций
Рассмотрим интеграл типа
![]() ,
гдеRобозначает рациональную
функцию своих аргументов
,
гдеRобозначает рациональную
функцию своих аргументов![]() и
и![]() .
Интеграл данного типа сводится к
интегралу от рациональной функции с
помощью так называемой универсальной
постановки
.
Интеграл данного типа сводится к
интегралу от рациональной функции с
помощью так называемой универсальной
постановки![]() .
.
Действительно,
![]() и
и
 =
=![]() .
.
Тогда,
подставляя в данный интеграл вместо
![]() ,
,![]() и
и![]() полученные выражения, будем иметь под
знаком интеграла рациональную функцию.
полученные выражения, будем иметь под
знаком интеграла рациональную функцию.
Пример13.Вычислить интеграл![]() .
.
Решение.
Подстановка![]() дает:
дает:
![]() =
=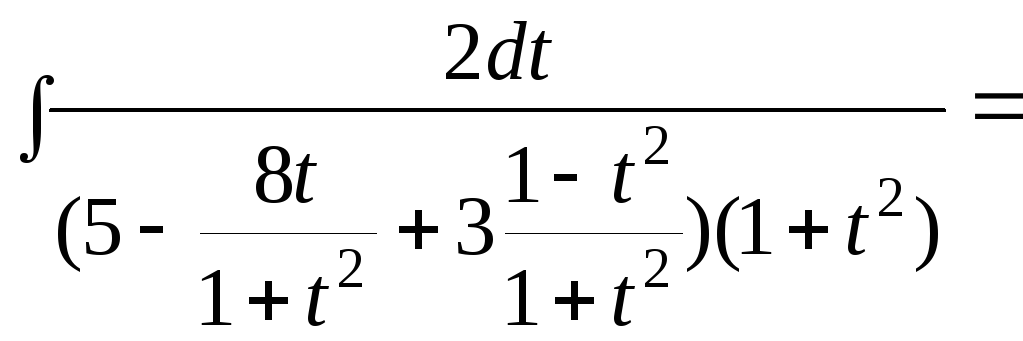
![]() =
=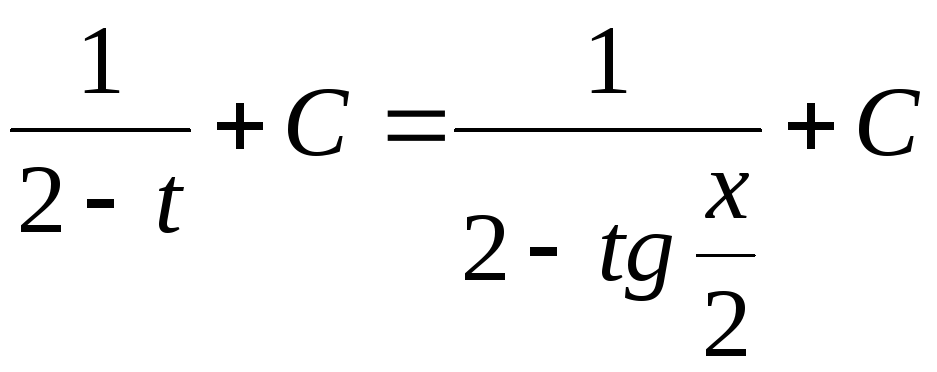 .
.
Универсальная подстановка нередко приводит к сложным вычислениям. Поэтому в указанных ниже случаях предпочтительней частные подстановки, также рационализирующие интеграл.
если
![]() ,
то применима подстановка
,
то применима подстановка![]() ;
;
если
![]() ,
то применима подстановка
,
то применима подстановка![]() ;
;
если
![]() ,
то применима подстановка
,
то применима подстановка![]() .
.
Пример14.
Вычислить интеграл![]() .
.
Решение.
Положим![]() и найдем:
и найдем:
![]() поэтому:
поэтому:![]()
![]() =
=![]() =
=![]() =
=![]() .
.
Рассмотрим интеграл вида
![]() ,
гдеmиn-целые
числа. Возможны следующие случаи:
,
гдеmиn-целые
числа. Возможны следующие случаи:
1. Одно из чисел mилиn– нечетное, например![]() ,
тогда полагая
,
тогда полагая![]() ,
получим:
,
получим:
![]() =
=![]() =
=![]()
![]()
2. Оба числа mиn– четные. Тогда рекомендуется воспользоваться тригонометрическими формулами понижения степени:
![]()
![]() .
.
Пример15.
Вычислить интеграл![]() .
.
Решение.
![]() =
=![]()
![]() =
=![]() .
.
Интегрирование некоторых иррациональных функций
Рассмотрим интеграл следующего вида:
![]() ,
,
где
R- рациональная функция,![]() - рациональные числа. Данный интеграл
сводится к интегралу от рациональной
функции с помощью подстановки
- рациональные числа. Данный интеграл
сводится к интегралу от рациональной
функции с помощью подстановки![]() ,
гдеk- общий знаменатель
всех дробных показателей.
,
гдеk- общий знаменатель
всех дробных показателей.
Пример16.Вычислить интеграл![]() .
.
Решение. Положив![]() ,
получим:
,
получим:![]() =
=![]()
![]()
![]() =
=![]() =
=![]() .
.
Контрольные задания
Вычислить неопределенные интегралы.
5.1
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
5.2
![]()
![]()
![]()
![]()
![]()
![]() .
.
5.3![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
5.4![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
5.5![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
5.6![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
5.7![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
5.8![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
5.9![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
5.1![]() 0
0![]()
![]()
![]()
![]()
![]()
![]() .
.
5.1![]() 1
1![]()
![]()
![]()
![]()
![]()
![]() .
.
5.12
![]()
![]()
![]()
![]()
![]()
![]() .
.
5.13
![]()
![]()
![]()
![]()
![]()
![]() .
.
5.14
![]()
![]()
![]()
![]()
![]()
![]() .
.
5.15
![]()
![]()
![]()
![]()
![]()
![]() .
.
5.16
![]()
![]()
![]()
![]()
![]()
![]() .
.
5.17
![]()
![]()
![]()
![]()
![]()
![]() .
.
5.18
![]()
![]()
![]()
![]()
![]()
![]() .
.
5.19
![]()
![]()
![]()
![]()
![]()
![]() .
.
5.20
![]()
![]()
![]()
![]()
![]()
![]() .
.
Указания к заданию 6 тема 6. Определенный интеграл
Пусть функция
![]() определена на отрезке
определена на отрезке![]() .
Разобьем этот промежуток произвольным
образом наnчастей точками
.
Разобьем этот промежуток произвольным
образом наnчастей точками
![]() .
.
В каждом из полученных частичных
промежутков
![]() ,
где
,
где![]() ,
выберем произвольную точку
,
выберем произвольную точку![]() .
Вычислим значение функции
.
Вычислим значение функции![]() и умножим его на разность
и умножим его на разность![]() ,
после этого составим сумму
,
после этого составим сумму![]() ,
которая называетсяинтегральной
суммой Римана для функции
,
которая называетсяинтегральной
суммой Римана для функции![]() на отрезке
на отрезке![]() .
.
Пусть
![]() ,
т.е. длина наибольшего частичного
промежутка. Если существует конечный
предел интегральной суммы
,
т.е. длина наибольшего частичного
промежутка. Если существует конечный
предел интегральной суммы![]() при
при![]() ,
не зависящий ни от способа разбиения
промежутка
,
не зависящий ни от способа разбиения
промежутка![]() на части, ни от выбора точек
на части, ни от выбора точек![]() ,
то этот предел называетсяопределенным
интеграломфункции
,
то этот предел называетсяопределенным
интеграломфункции![]() на промежутке
на промежутке![]() и обозначается символом
и обозначается символом![]() .
Таким образом,
.
Таким образом,![]()
![]() .
.
Функция
![]() в этом случае называетсяинтегрируемойв промежутке
в этом случае называетсяинтегрируемойв промежутке![]() .
Числа
.
Числа![]() и
и![]() называются соответственно нижним и
верхним пределами интеграла.
называются соответственно нижним и
верхним пределами интеграла.
Выясним геометрический смысл суммы
Римана
![]() ,
когда функция
,
когда функция![]() непрерывна и неотрицательна в промежутке
непрерывна и неотрицательна в промежутке![]() ,
,![]() .
В этом случае произведение
.
В этом случае произведение![]() равно площади прямоугольника с основанием
равно площади прямоугольника с основанием![]() и высотой
и высотой![]() ,
а сумма
,
а сумма![]() равна сумме площадей прямоугольников
с основанием
равна сумме площадей прямоугольников
с основанием![]() и высотами
и высотами![]() (рис. 1).
(рис. 1).
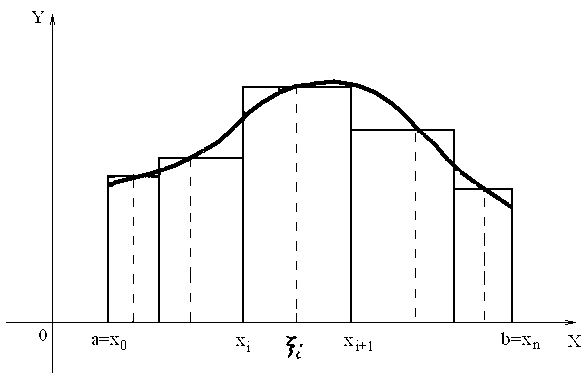
Рис.1
Таким образом,
![]() равна площади ступенчатой фигуры, а
определенный интеграл равен пределу
равна площади ступенчатой фигуры, а
определенный интеграл равен пределу![]() при
при![]() ,
т.е. площади криволинейной трапеции,
ограниченной графиком функции
,
т.е. площади криволинейной трапеции,
ограниченной графиком функции![]() ,
прямыми
,
прямыми![]() и
и![]() и отрезком
и отрезком![]() оси
оси![]() .
.
Свойства определенного интеграла
Пусть все рассматриваемые функции являются непрерывными, так что определенные интегралы от них существуют. Тогда справедливы следующие соотношения:
1.
![]()
![]()
![]()
2.
![]()
![]()
3.
![]()
![]()
4.
![]()
![]()
![]()
5.
![]()
6. Если
![]() .
.
Если функции
![]() непрерывна на отрезке
непрерывна на отрезке![]() и
и![]() -
какая-нибудь первообразная для
-
какая-нибудь первообразная для![]() на этом отрезке, то справедлива формула
Ньютона-Лейбница:
на этом отрезке, то справедлива формула
Ньютона-Лейбница:
![]() .
.
Правую часть формулы часто обозначают
символом
![]() (знак двойной подстановки от
(знак двойной подстановки от![]() до
до![]() ).
).
Пример1.
Вычислить определенный интеграл![]() .
.
Решение.
![]() .
.
Замена переменной в определенном интеграле
Пусть функция
![]() непрерывна на отрезке
непрерывна на отрезке![]() ,
а функция
,
а функция![]() определена и непрерывна вместе со своей
производной
определена и непрерывна вместе со своей
производной![]() на отрезке
на отрезке![]() ,
причем
,
причем![]() для любого
для любого![]() и
и![]() ,
,![]()
Тогда:
![]()
![]()
Эта формула называется формулой замены переменной в определенном интеграле или формулой интегрирования подстановкой.
Пример2.Вычислить определенный интеграл![]() .
.
Решение.Сделаем замену переменной![]() .
.
Тогда
![]() .
Пересчитаем пределы интегрирования:
при
.
Пересчитаем пределы интегрирования:
при![]()
![]() ,
а при
,
а при![]()
![]() .
.
![]()
![]()
![]() .
.
Заметим, что при вычислении определенного интеграла к старой переменной не возвращаются.
Интегрирование по частям в определенном интеграле
Теорема. Если функции
![]() и
и![]() дифференцируемы на отрезке
дифференцируемы на отрезке![]() ,
то справедлива следующая формула
,
то справедлива следующая формула![]() .
.
Пример3.
Вычислить![]() .
.
Решение.
Обозначим![]() ,
,![]() .
.
Тогда
![]() ,
,![]() .
.
![]()
![]() .
.
Геометрические приложения определенного интеграла
Площадь плоской фигуры
Площадь
![]() криволинейной трапеции, ограниченной
графиком
криволинейной трапеции, ограниченной
графиком![]() ,
осью
,
осью![]() и прямыми
и прямыми![]() и
и![]() (рис.2) вычисляется по следующей формуле:
(рис.2) вычисляется по следующей формуле:![]()
Если
часть кривой
![]() находится под осью
находится под осью![]() (рис.3), то площадь заштрихованной фигуры
равна:
(рис.3), то площадь заштрихованной фигуры
равна:
![]() .
.![]()
Пусть фигура ограничена двумя кривыми
![]() ,
,
![]() и
и![]() ,
,![]() (рис. 4). Тогда ее площадь вычисляется
по формуле
(рис. 4). Тогда ее площадь вычисляется
по формуле![]() .
.
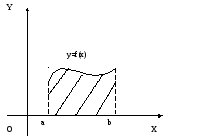
Рис.2

Рис. 3

Рис. 4
Пример4.Вычислить площадь фигуры, ограниченной
прямой![]() и параболой
и параболой![]() .
.
Решение.Построим графики прямой и параболы
(рис. 5).
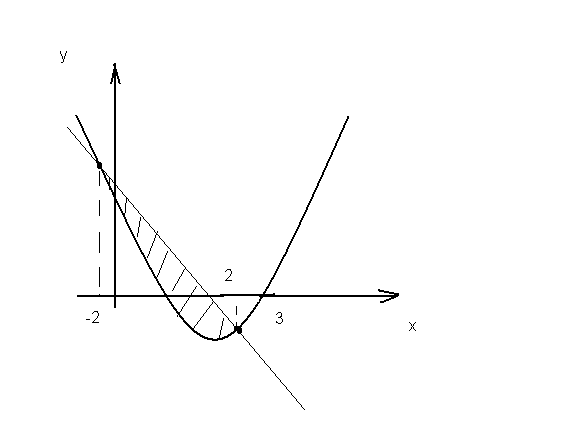
Рис. 5.
Найдем точки пересечения параболы и прямой:
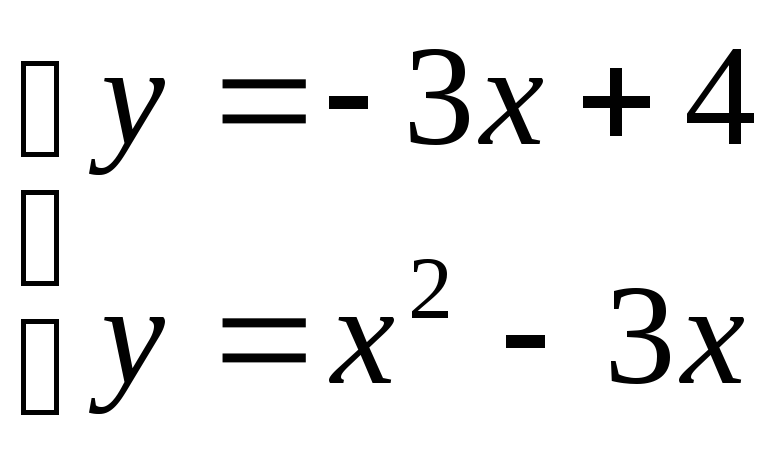
![]()
![]() .
.
Тогда получим:
![]() .
.
