
- •Практикум з курсу
- •Метричні й топологічні простори Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Варіант 5
- •Варіант 6
- •Варіант 7
- •Варіант 8
- •Варіант 9
- •Скрізь щільні та ніде не щільні множини. Сепарабельні простори. Неперервні відображення Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 8
- •Варіант 9
- •4.Аксіоми зчисленності та відокремленості. Нормальні простори. Гомеоморфні простори Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Варіант 5
- •Варіант 6
- •Варіант 7
- •Варіант 7
- •Варіант 4
- •Список рекомендованої літератури
Варіант 8
Знайти всі граничні, межові, ізольовані та внутрішні точки множин:
а)
![]()
![]() \
\![]() )
)![]()
![]() ;
;
б)
![]() |
|
![]()
![]() .
.
Ці множини є відкритими чи замкненими?
Знайти замикання всіх точок вигляду
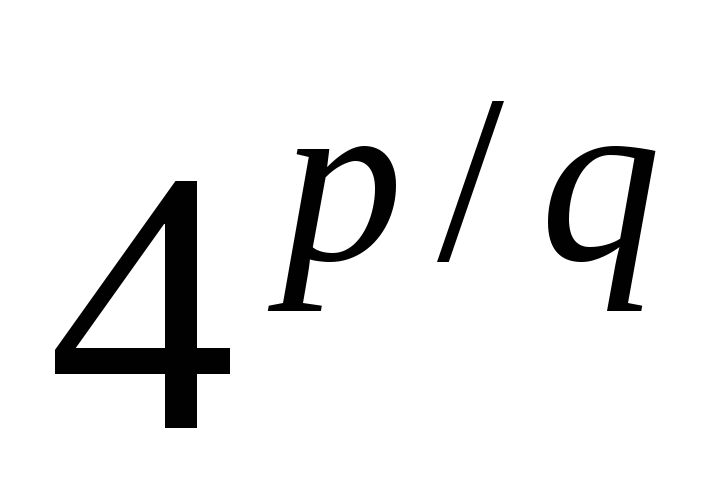 ,
де
,
де
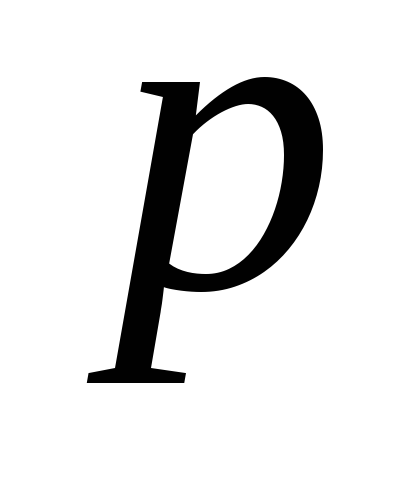 –
від’ємне ціле число, а
–
від’ємне ціле число, а
 –
натуральне.
–
натуральне.Нехай
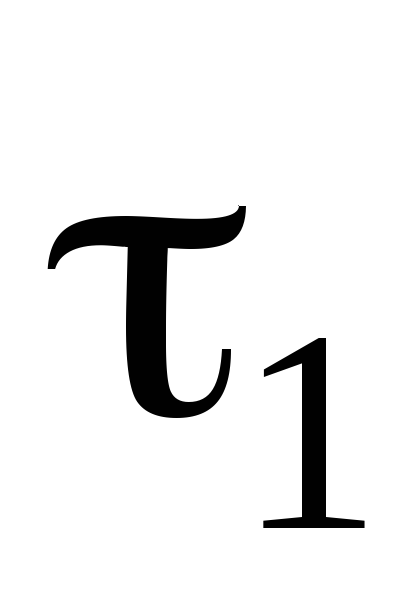 і
і
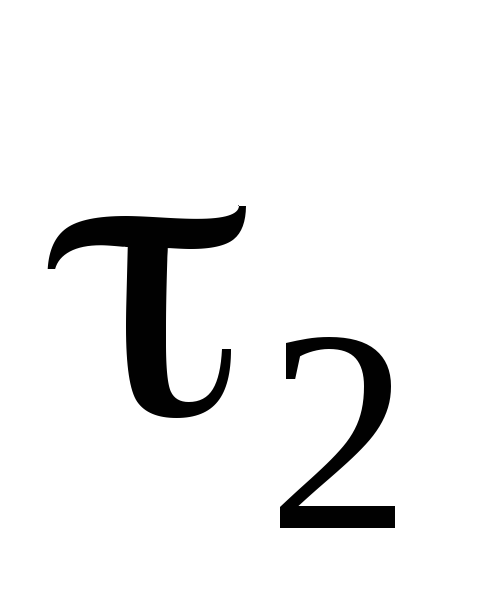 -
топології на
-
топології на
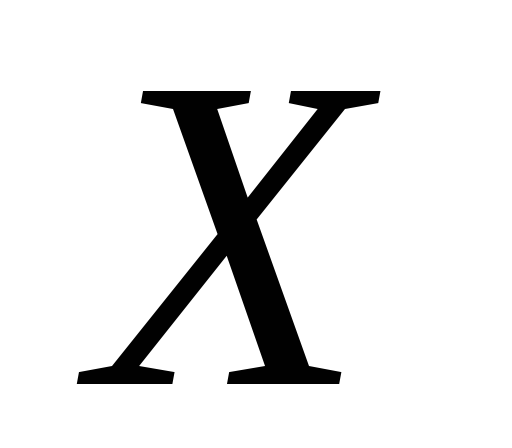 такі,
що
такі,
що
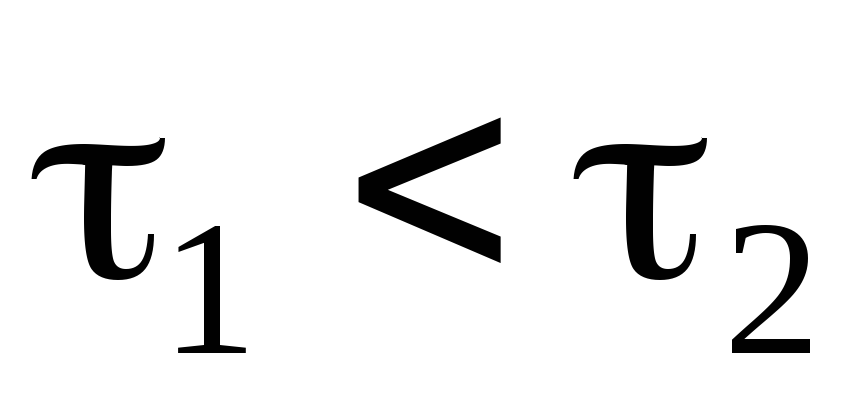 .
Нехай далі
.
Нехай далі
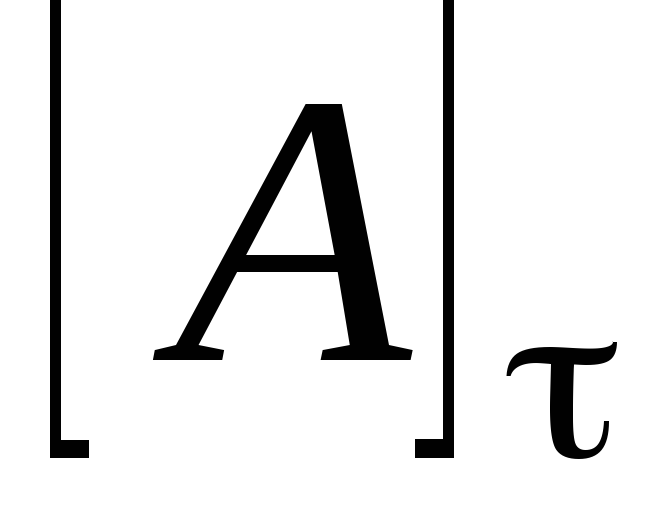 –
замикання множини
–
замикання множини
 відносно
відносно
 .
Довести, що
.
Довести, що
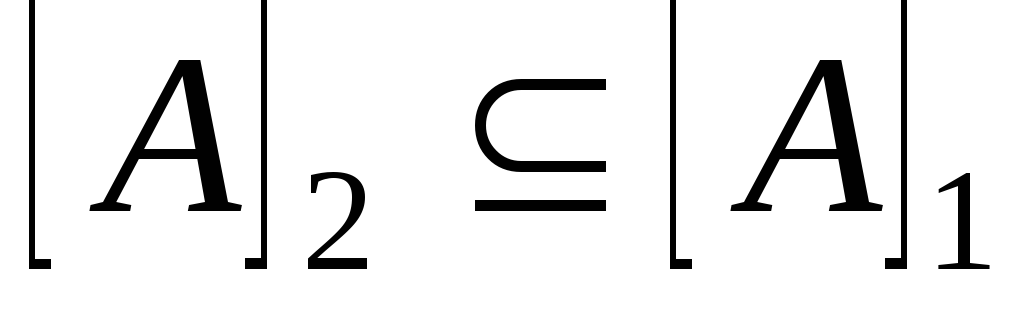 для
для
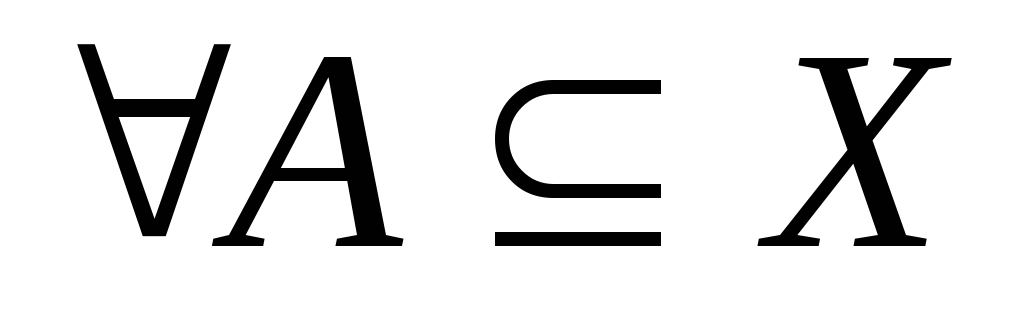 .
.Довести, що
 для будь-якої множини
для будь-якої множини
 топологічного простору
топологічного простору
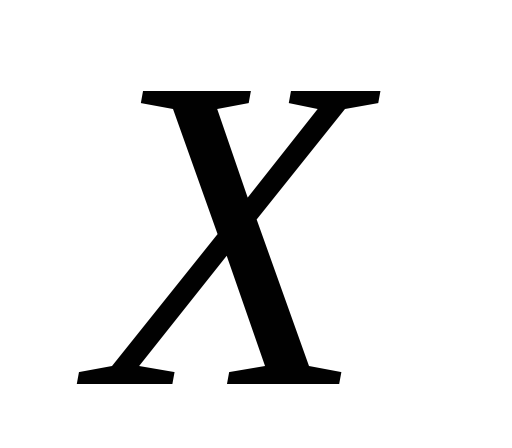 .
.Довести, що підмножина
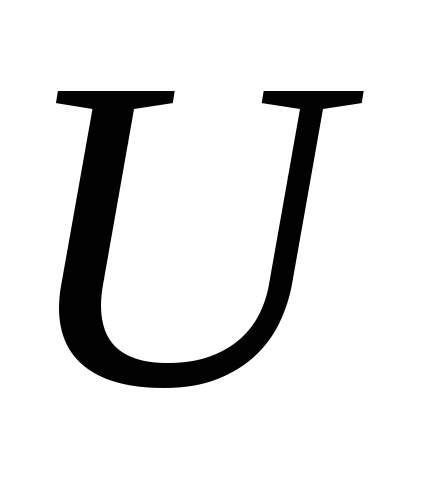 метричного простору
метричного простору відкрита тоді і тільки тоді, коли
відкрита тоді і тільки тоді, коли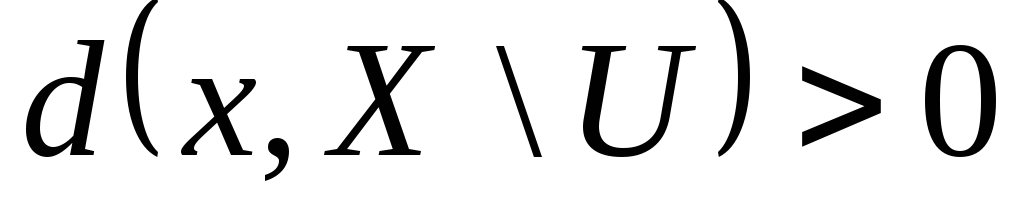 для
для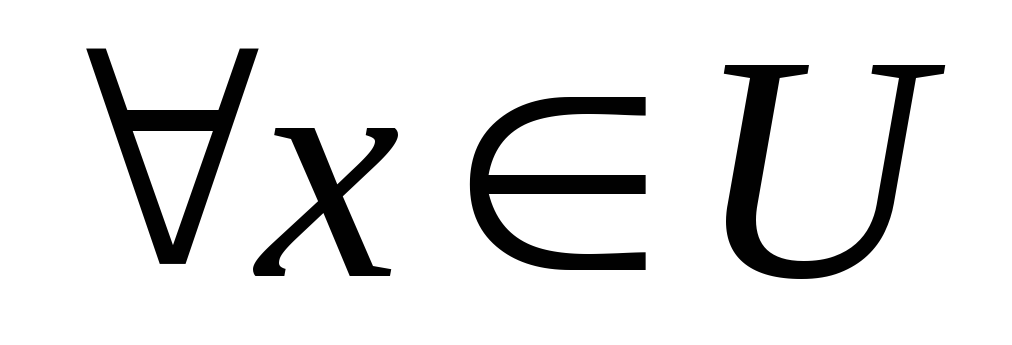 .
.
Варіант 9
Знайти всі граничні, межові, ізольовані та внутрішні точки множин:
а)
![]()
![]() \
\![]() )
)![]()
![]() ;
;
б)
![]() |
|
![]()
![]() .
.
Ці множини є відкритими чи замкненими?
Знайти замикання всіх точок вигляду
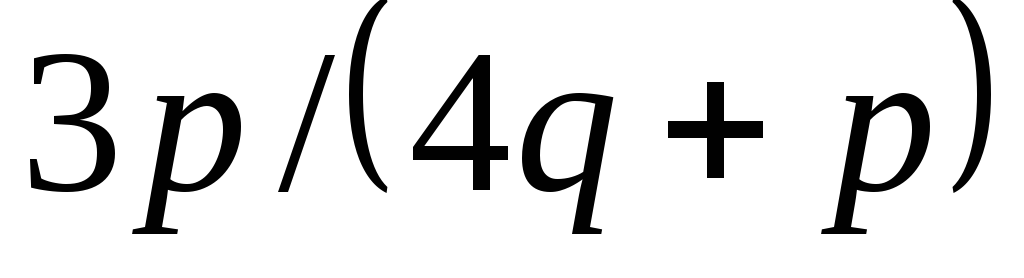 ,
де
,
де
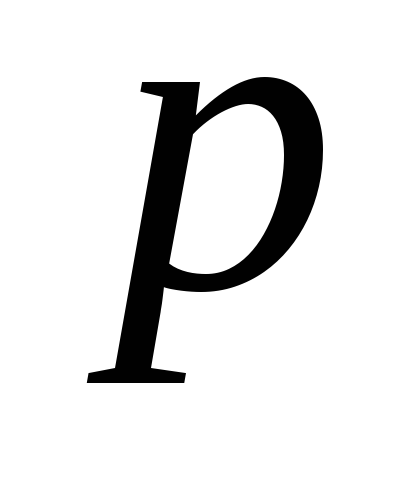 – від’ємне ціле число, а
– від’ємне ціле число, а
 –
натуральне.
–
натуральне.Нехай
 – підпростір топологічного простору
– підпростір топологічного простору
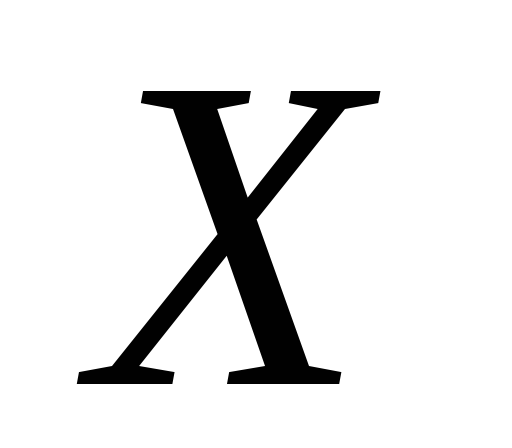 і
і
 .
Нехай також
.
Нехай також
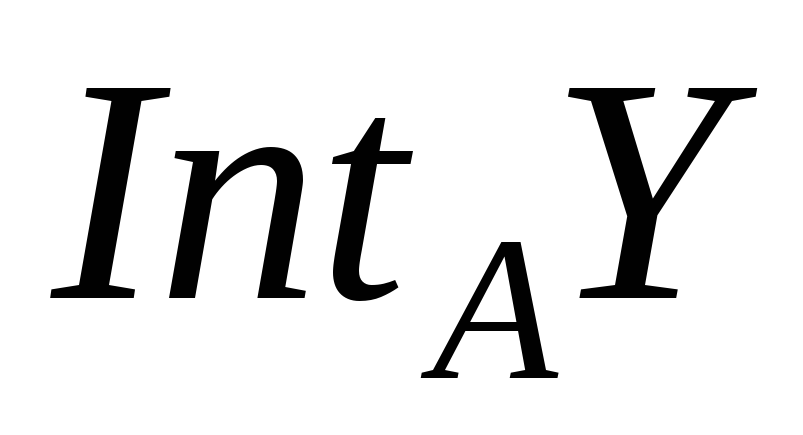 – внутрішність
– внутрішність
 в
в
 ,
,
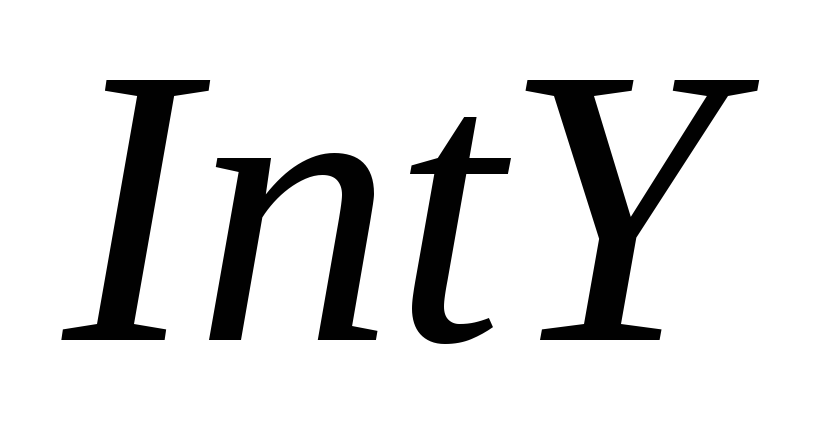 – внутрішність
– внутрішність
 в
в
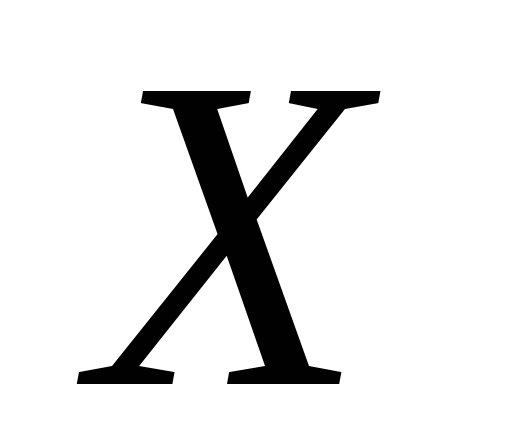 .
Чи вірно, що
.
Чи вірно, що
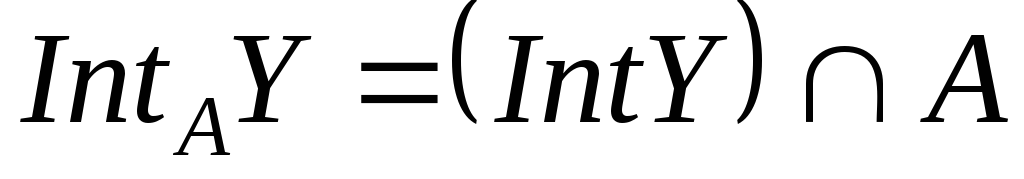 ?
?Довести, що ізольована точка
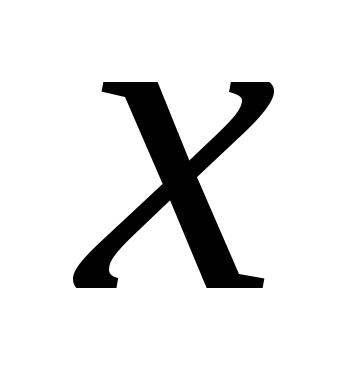 множини
множини
 топологічного простору
топологічного простору
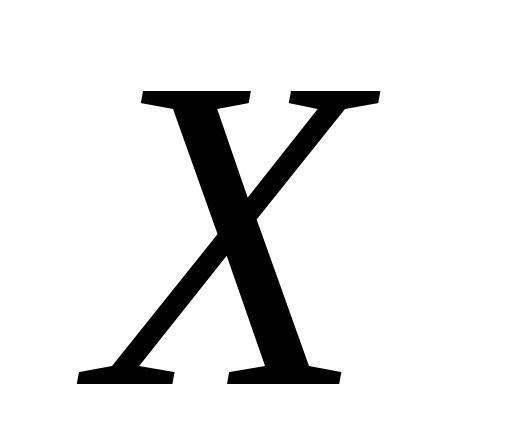 належить
належить
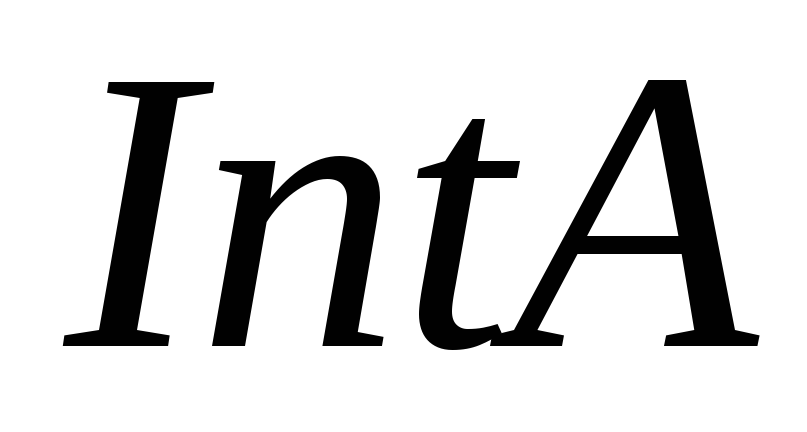 тоді
й тільки тоді, коли множина
тоді
й тільки тоді, коли множина
 відкрита в
відкрита в
 .
У противному разі точка
.
У противному разі точка
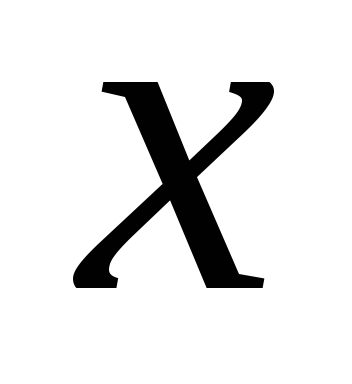 є межовою точкою
є межовою точкою
 .
.Визначити, чи дійсно
 .
Чи буде
.
Чи буде
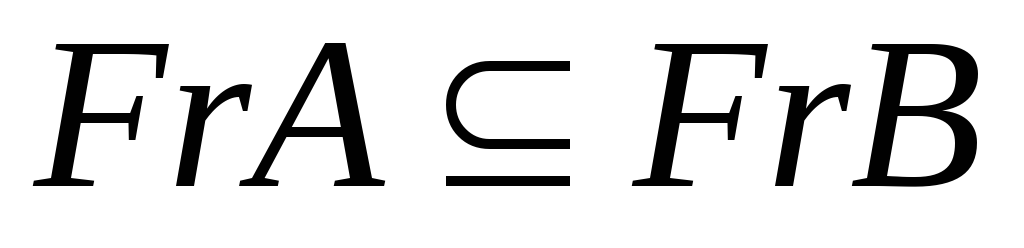 ,
якщо
,
якщо
 ?
?
Скрізь щільні та ніде не щільні множини. Сепарабельні простори. Неперервні відображення Варіант 1
Довести, що підмножина
 топологічного простору
топологічного простору
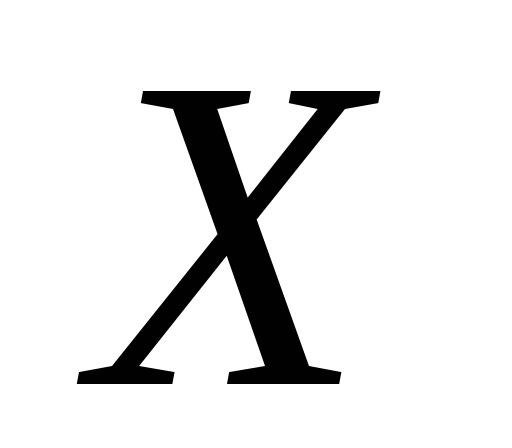 ніде
не щільна тоді і тільки тоді, коли
ніде
не щільна тоді і тільки тоді, коли
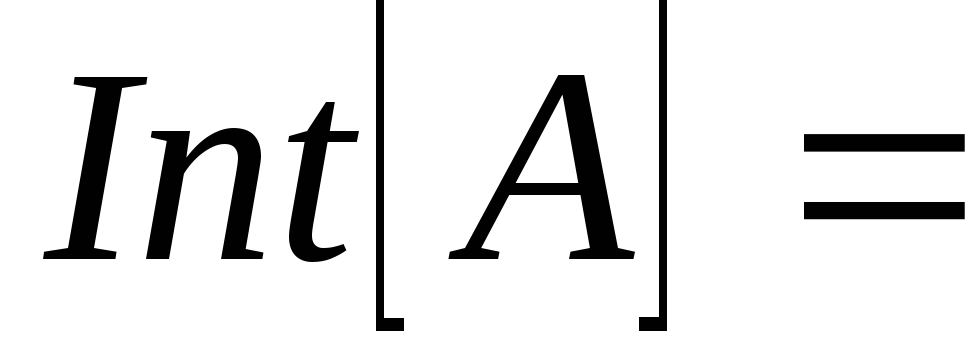
 .
.Довести, що для будь-якої відкритої підмножини
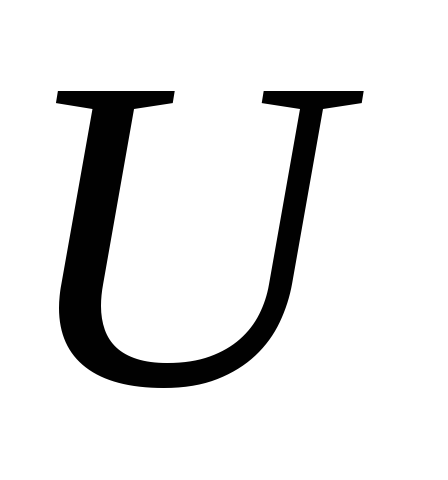 в топологічному просторі
в топологічному просторі
 множина
множина
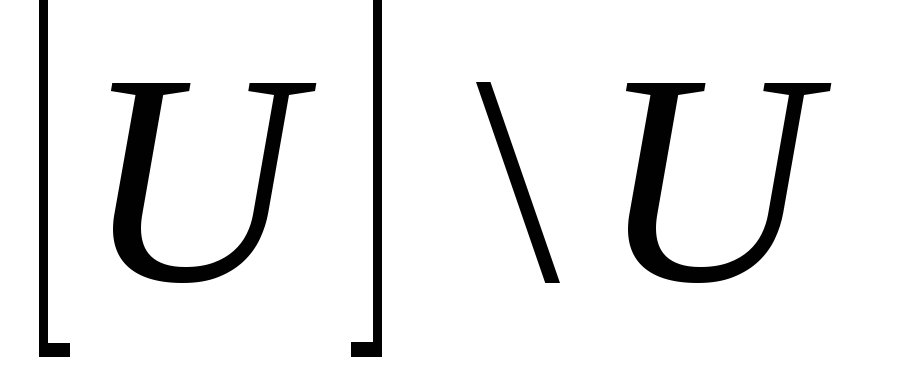 ніде не щільна.
ніде не щільна.Довести, що в сепарабельному топологічному просторі множина всіх ізольованих точок є зчисленною (нескінченною або скінченною).
Довести, що топологічний простір є дискретний тоді і тільки тоді, коли кожне його відображення у топологічний простор неперервне.
Варіант 2
Навести приклад послідовності скрізь щільних множин
 на прямій, таких, що
на прямій, таких, що
 , а
також
, а
також
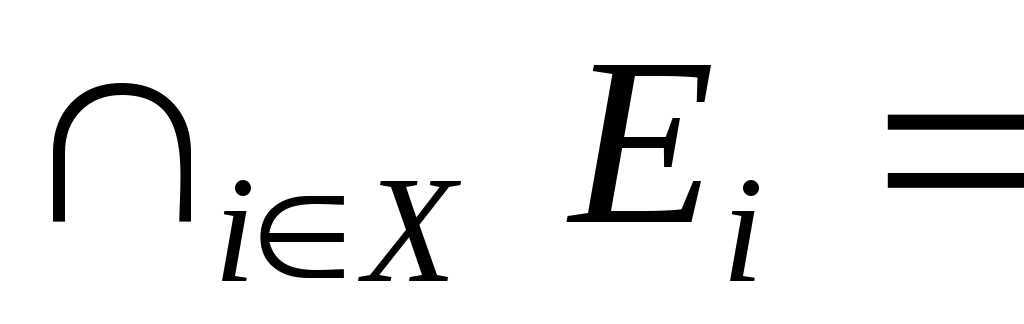
 .
.Довести, що топологічний простір буде дискретним тоді і тільки тоді, коли скрізь щільною множиною в ньому буде тільки він самий. Подати прямий опис скрізь щільних множин у топології стрілки.
Довести, що в сепарабельному топологічному просторі будь-яка сім'я не порожніх відкритих неперетинних множин буде зчисленною (нескінченною або скінченною).
Довести, що відображення
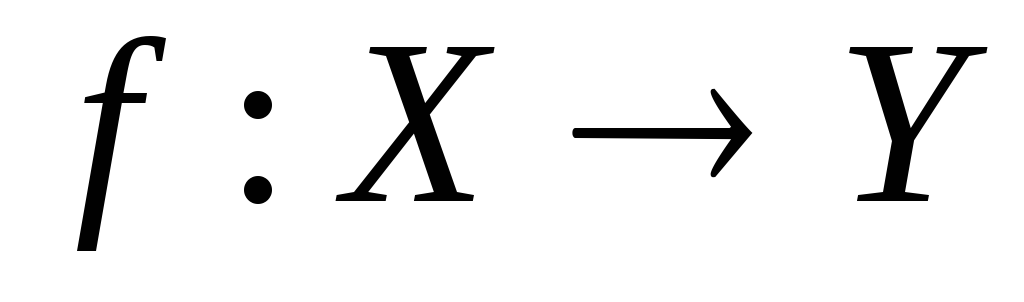 топологічних просторів
топологічних просторів
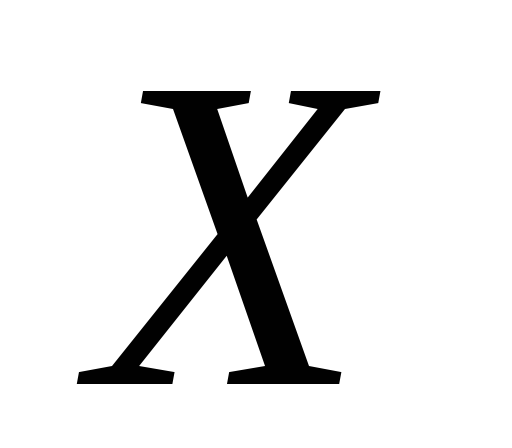 та
та неперервне тоді і тільки тоді, коли для
кожного елемента
неперервне тоді і тільки тоді, коли для
кожного елемента деякої
бази β простору
деякої
бази β простору
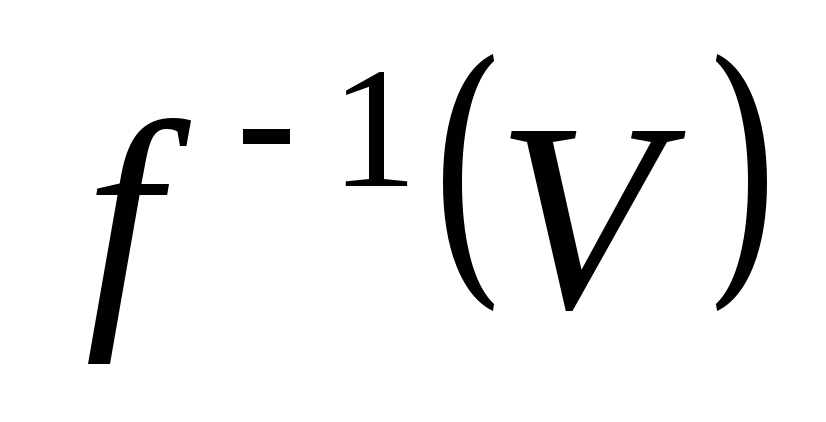 є відкрита множина в
є відкрита множина в
 .
.
Варіант 3
Довести, що множина
 топологічного простору
топологічного простору
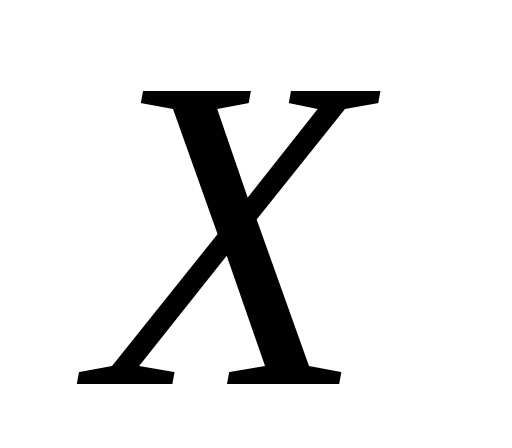 ніде
не щільна в
ніде
не щільна в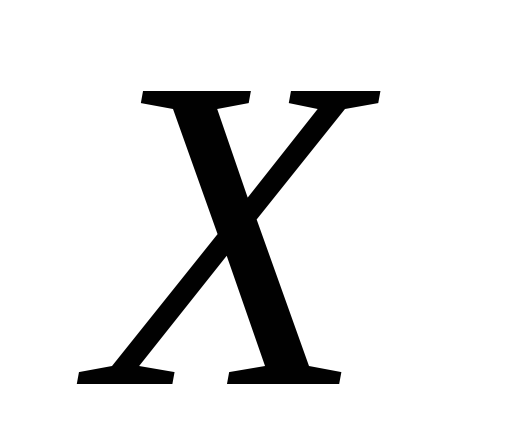 тоді і тільки тоді, коли в будь-якій не
порожній відкритій множині
тоді і тільки тоді, коли в будь-якій не
порожній відкритій множині існує така не порожня відкрита підмножина
існує така не порожня відкрита підмножина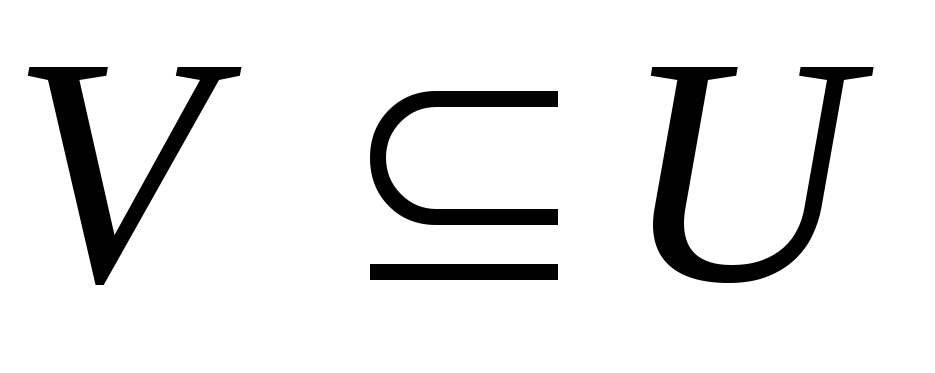 ,
що
,
що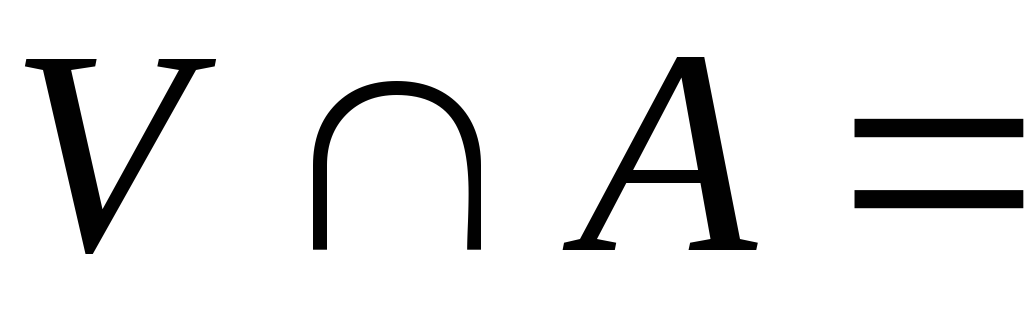
 .
.Довести, що межа замкненої множини ніде не щільна.
Довести, що топологічний добуток скінченної кількості сепарабельних просторів – сепарабельний.
Довести, що відображення
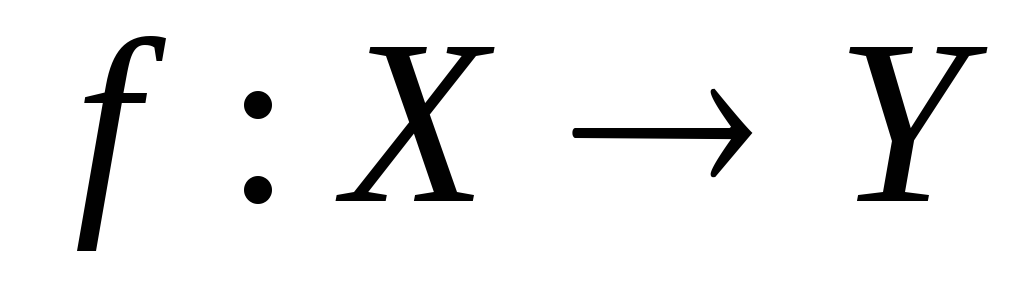 топологічних просторів
топологічних просторів
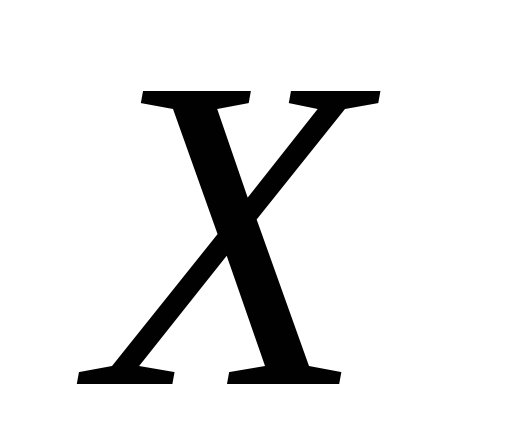 та
та неперервне тоді і тільки тоді, коли
неперервне тоді і тільки тоді, коли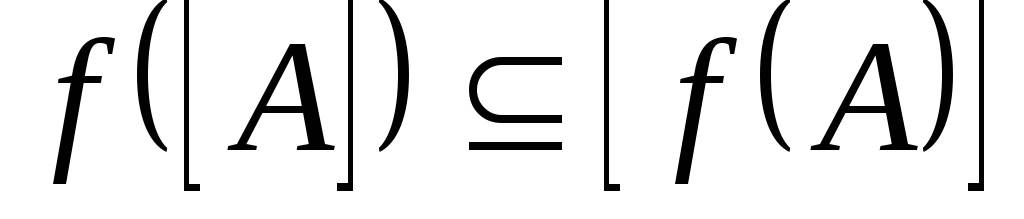 для кожної множини
для кожної множини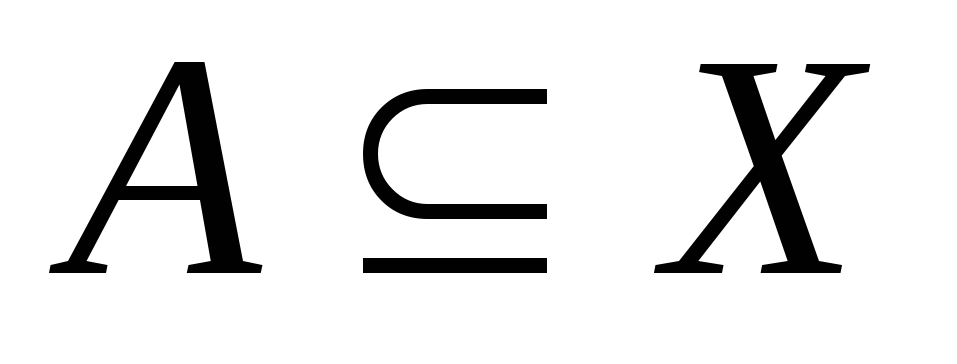 .
.
Варіант 4
Довести, що множина
 топологічного простору
топологічного простору
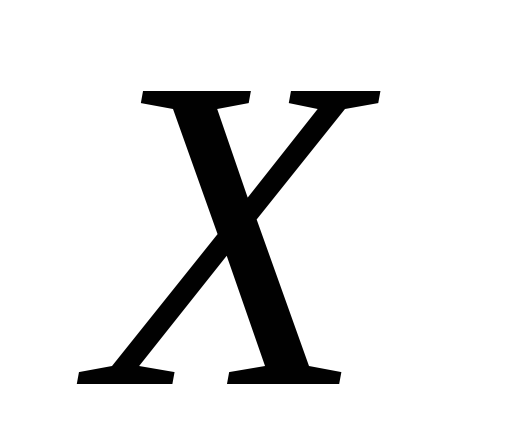 скрізь
щільна в
скрізь
щільна в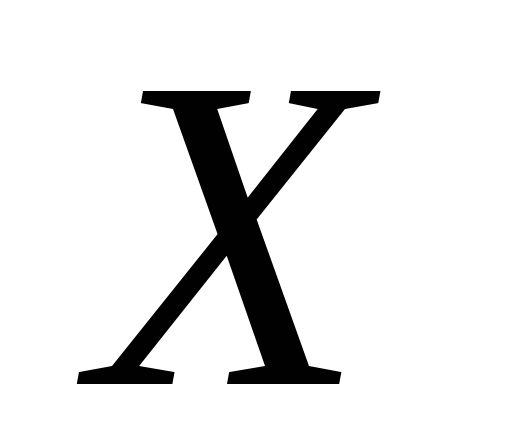 тоді і тільки тоді, коли
тоді і тільки тоді, коли
 для будь-якої не порожньої відкритої
підмножини
для будь-якої не порожньої відкритої
підмножини .
.Нехай
 і
і
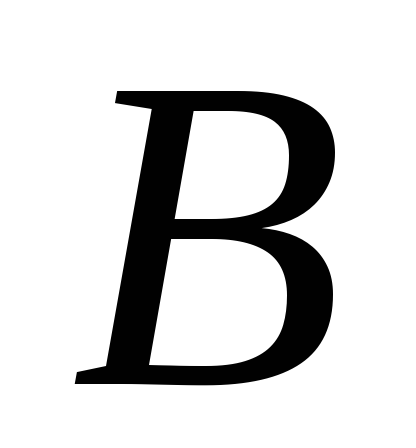 –
скрізь щільні підмножини топологічного
простору
–
скрізь щільні підмножини топологічного
простору
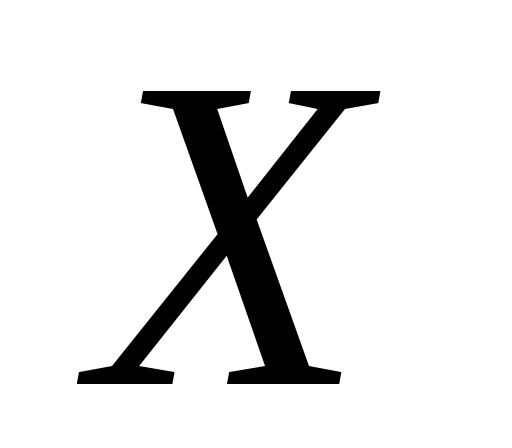 і
і
 –
відкрита в
–
відкрита в
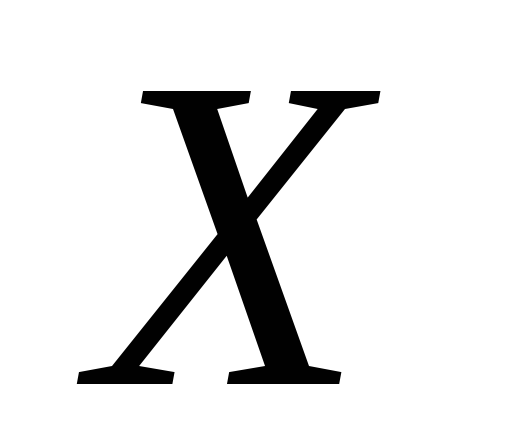 .
Довести, що
.
Довести, що
 є
скрізь щільна множина в
є
скрізь щільна множина в
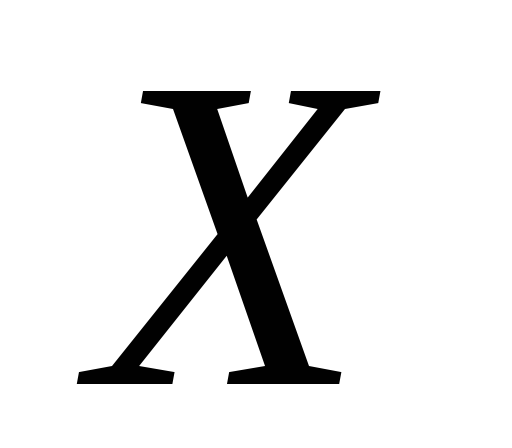 .
.Довести, що будь-який підпростір сепарабельного метризованого простору – сепарабельний.
Визначити, чи буде замкнене відображення одного топологічного простору на інший також відкритим.
Варіант 5
Множина
 –
ніде не щільна в топологічному просторі
–
ніде не щільна в топологічному просторі
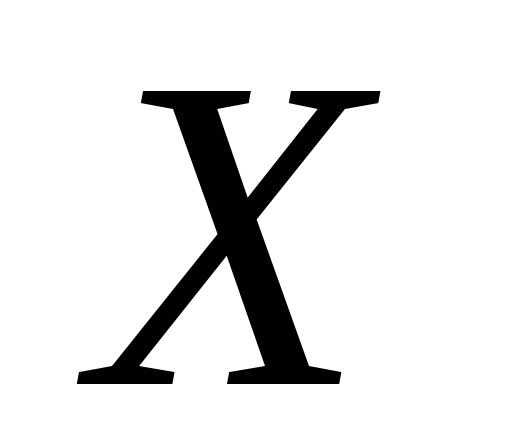 .
Що можна сказати про
.
Що можна сказати про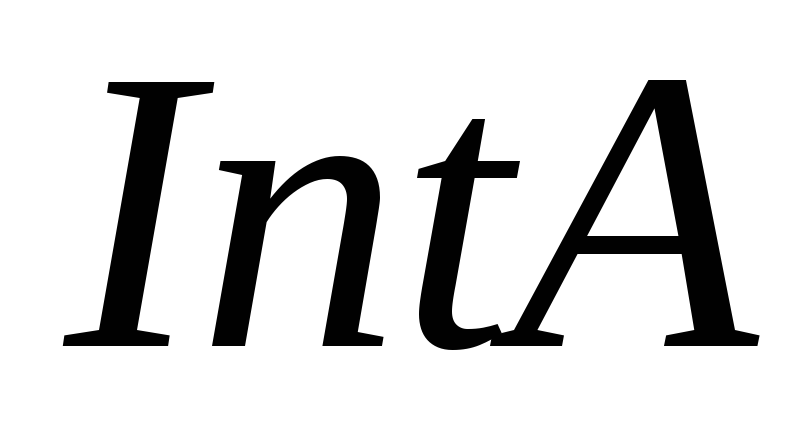 ,
,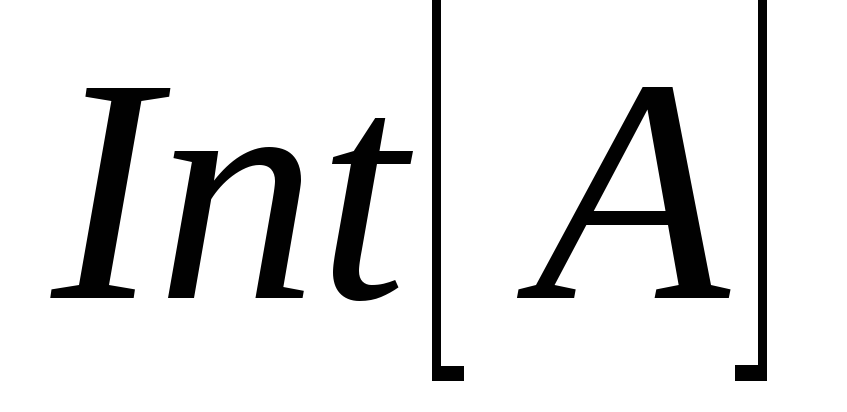 і
і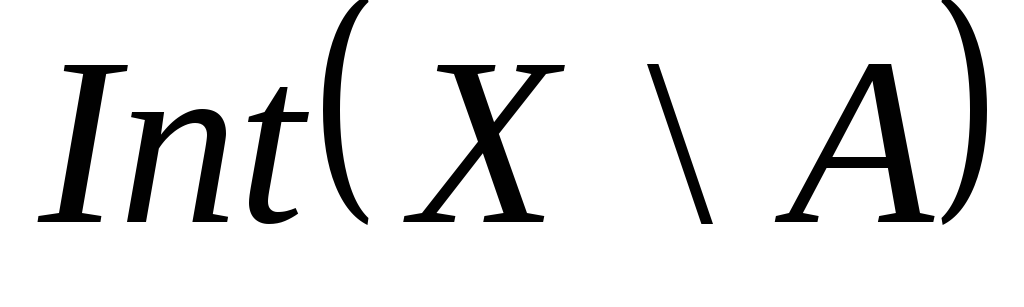 ?
?Навести прямий опис множин скрізь щільних у тривіальному просторі та в просторі скінченний доповнень.
Довести, що цілком обмежений метричний простір є сепарабельним.
Визначити, чи буде відкрите відображення одного топологічного простору на інший також замкненим.
Варіант 6
Довести, що підмножина
 топологічного простору
топологічного простору
 ніде не щільна в
ніде не щільна в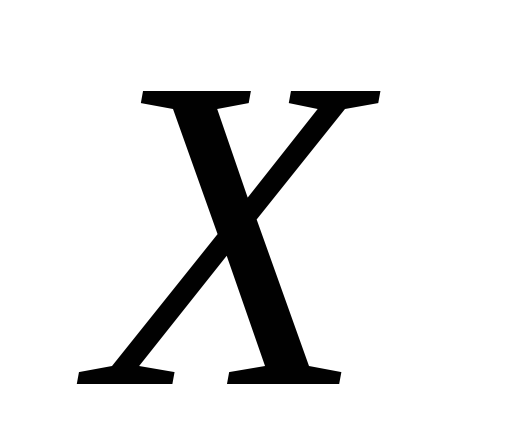 тоді і тільки тоді, коли в будь-якій не
порожній відкритій множині
тоді і тільки тоді, коли в будь-якій не
порожній відкритій множині існує така не порожня відкрита множина
існує така не порожня відкрита множина ,
що
,
що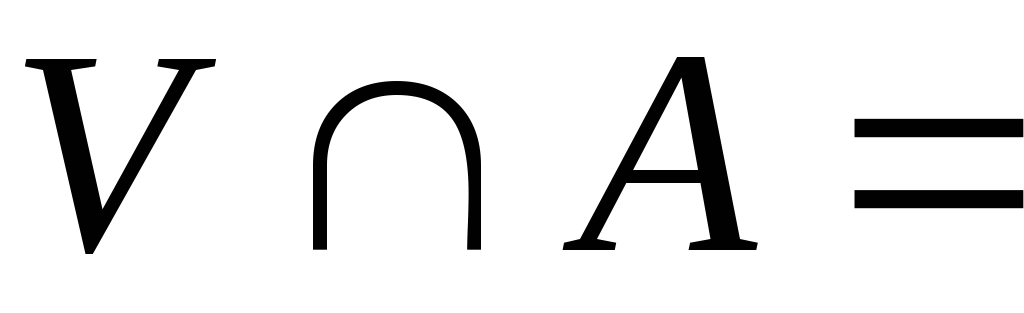
 .
.Довести, що об’єднання скінченного числа ніде не щільних в просторі
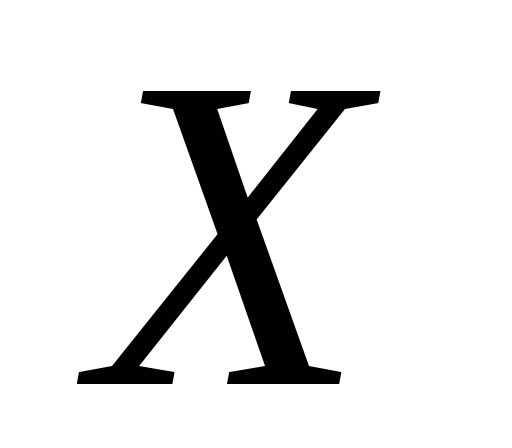 множин ніде не щільне в
множин ніде не щільне в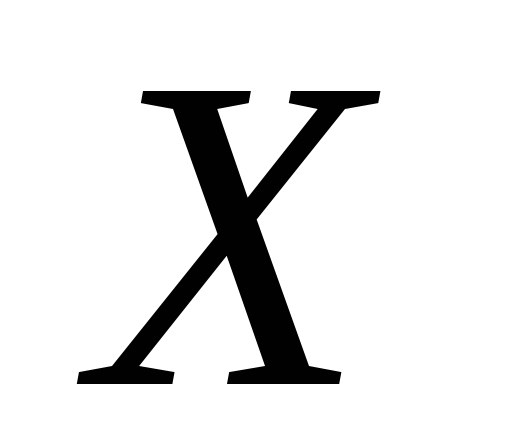 .
.Довести, що образ сепарабельного простору при неперервному відображенні буде сепарабельним.
Довести, що відображення
 топологічних просторів
топологічних просторів
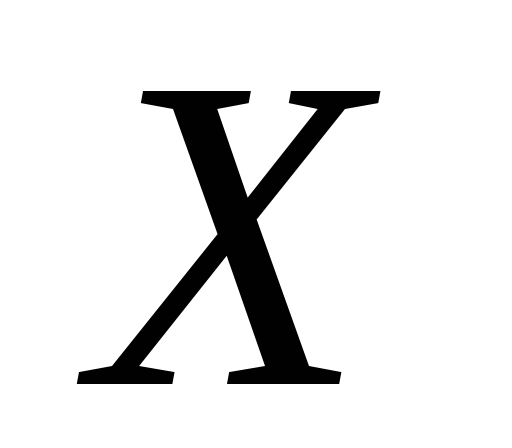 та
та замкнене тоді і тільки тоді, коли
замкнене тоді і тільки тоді, коли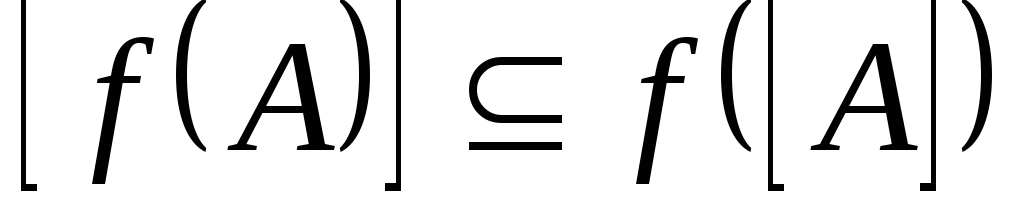 для будь-якої підмножини
для будь-якої підмножини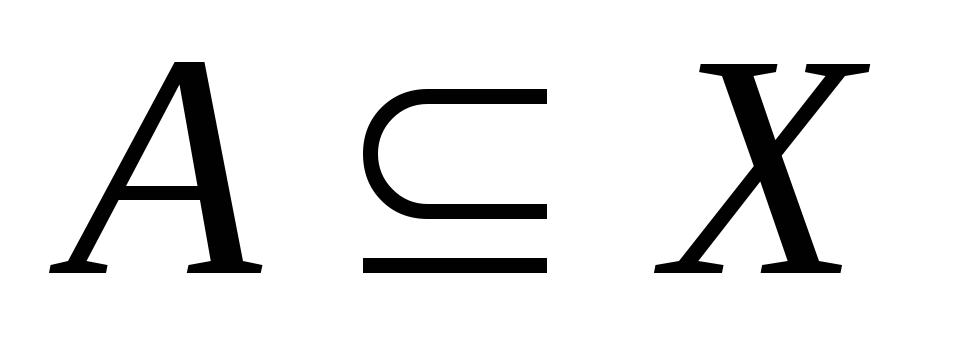 .
.
Варіант 7
Довести, що підмножина
 топологічного простору
топологічного простору
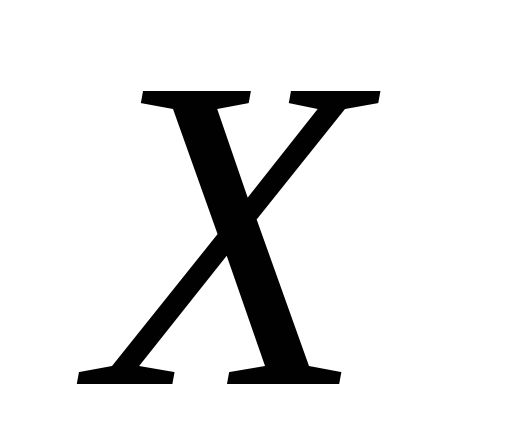 скрізь
щільна в
скрізь
щільна в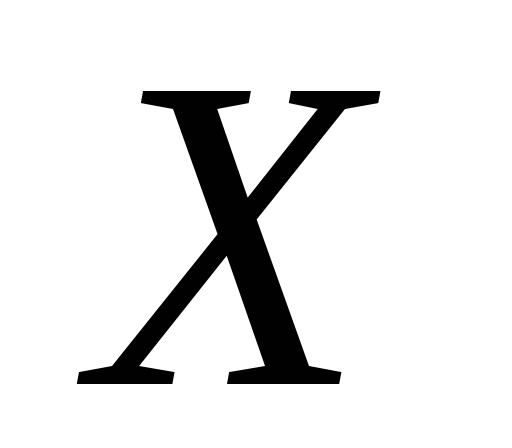 тоді і тільки тоді, коли
тоді і тільки тоді, коли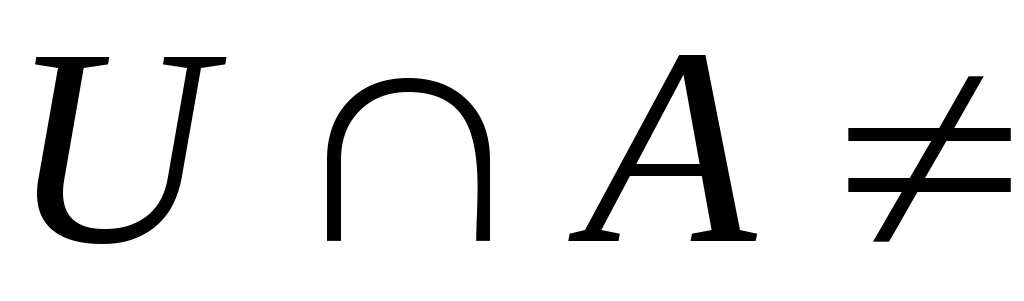
 для будь-якої не порожньої відкритої
підмножини
для будь-якої не порожньої відкритої
підмножини .
.Довести, що перетин скінченного числа відкритих скрізь щільних у просторі
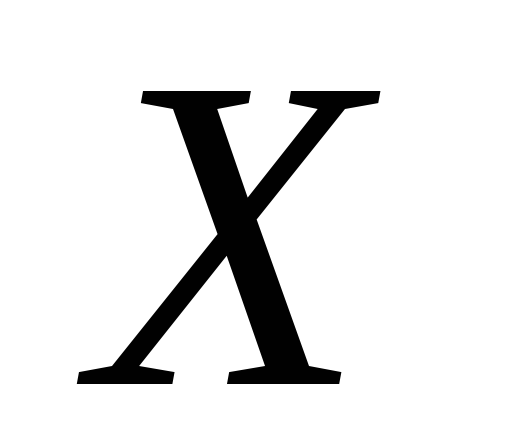 множин
буде скрізь щільним в
множин
буде скрізь щільним в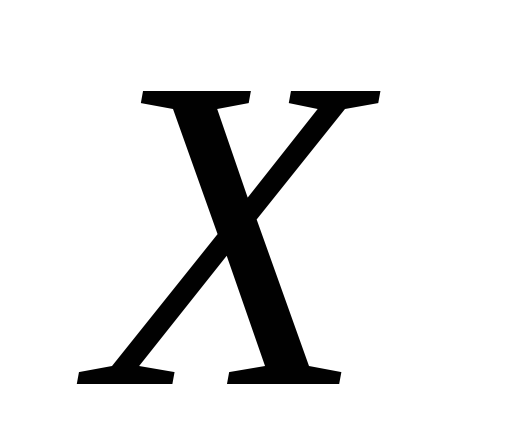 .
.Нехай
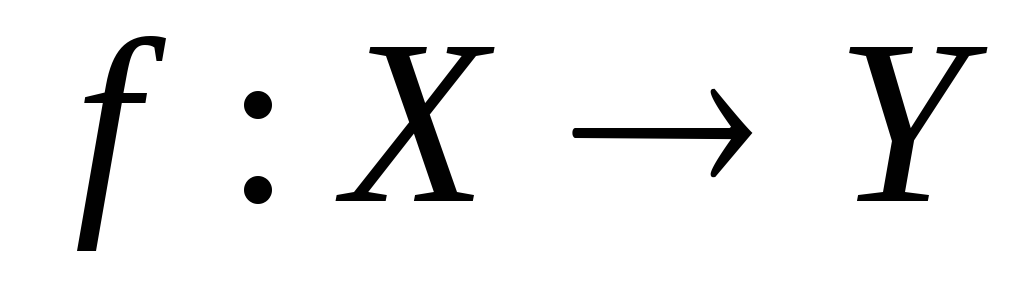 – неперервне сюр’єктивне
відображення топологічних просторів
та
– неперервне сюр’єктивне
відображення топологічних просторів
та
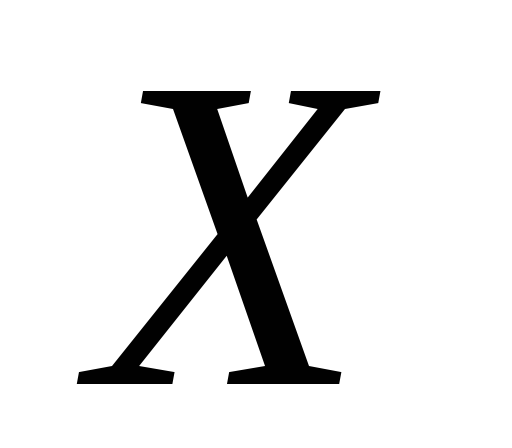 – сепарабельним топологічний простір.
Довести, що простір
– сепарабельним топологічний простір.
Довести, що простір –
сепарабельний.
–
сепарабельний.Довести, що відображення
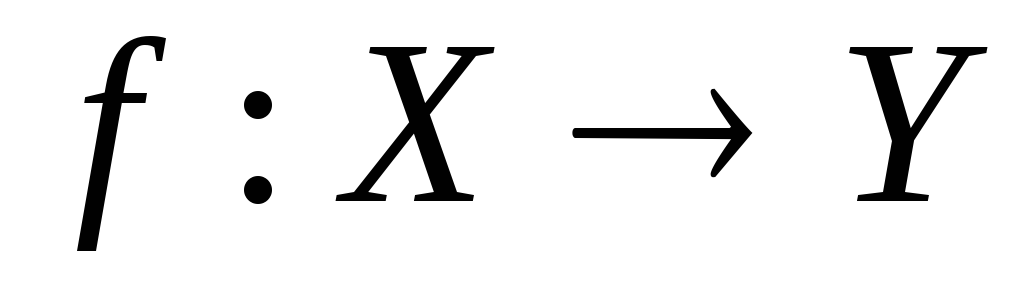 топологічних просторів
топологічних просторів
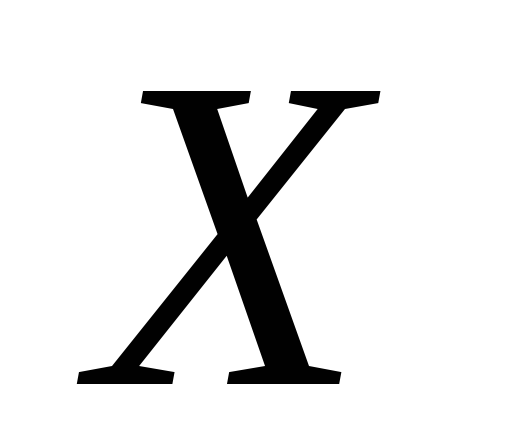 та
та відкрите тоді і тільки тоді, коли для
кожного елемента
відкрите тоді і тільки тоді, коли для
кожного елемента деякої
бази β простору
деякої
бази β простору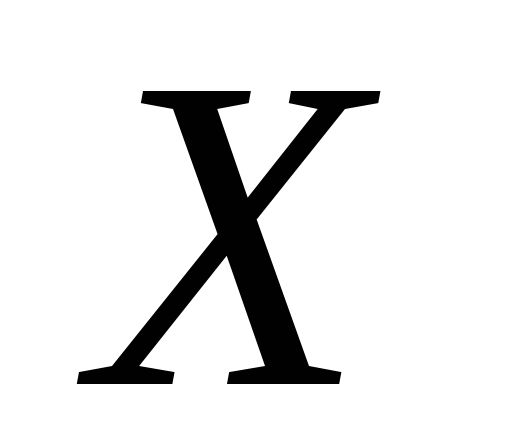
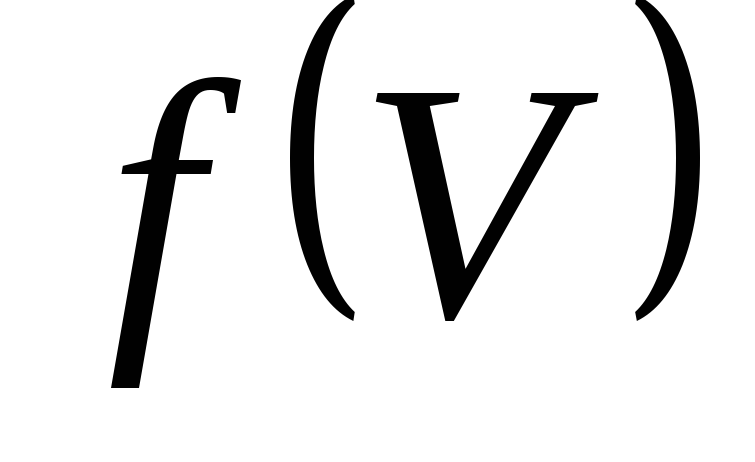 є відкрита множина в
є відкрита множина в
 .
.
