
- •Практикум з курсу
- •Метричні й топологічні простори Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Варіант 5
- •Варіант 6
- •Варіант 7
- •Варіант 8
- •Варіант 9
- •Скрізь щільні та ніде не щільні множини. Сепарабельні простори. Неперервні відображення Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 8
- •Варіант 9
- •4.Аксіоми зчисленності та відокремленості. Нормальні простори. Гомеоморфні простори Варіант 1
- •Варіант 2
- •Варіант 3
- •Варіант 4
- •Варіант 5
- •Варіант 6
- •Варіант 7
- •Варіант 7
- •Варіант 4
- •Список рекомендованої літератури
Варіант 7
Визначити, чи буде образ незв’язного простору при неперервному відображенні незв’язним.
Визначити, чи буде зв’язною множина точок площини, у яких хоча б одна з координат ірраціональна.
Нехай
 –
підмножина зв’язного топологічного
простору. Довести, що якщо
–
підмножина зв’язного топологічного
простору. Довести, що якщо
 –
зв’язна, то і
–
зв’язна, то і
 – зв’язна.
– зв’язна.Визначити, чи будуть гомеоморфними простори
 і
і 2
2
Варіант 8
З’ясувати, чи буде зв’язною множина точок усіх кіл на площині з радіусом
 (де
(де
 –
раціональне число) та центром на початку
координат.
–
раціональне число) та центром на початку
координат.Довести, що топологічний добуток
 – лінійно зв’язний тоді і тільки тоді,
коли простори
– лінійно зв’язний тоді і тільки тоді,
коли простори і
і
 лінійно зв’язні.
лінійно зв’язні.Нехай
 – зв’язна підмножина топологічного
простору
– зв’язна підмножина топологічного
простору
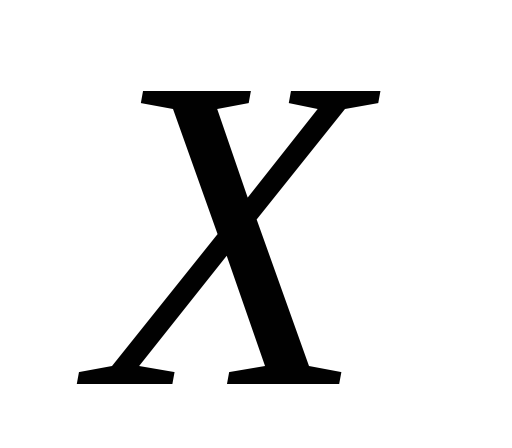 .
Довести, що якщо
.
Довести, що якщо ,
,
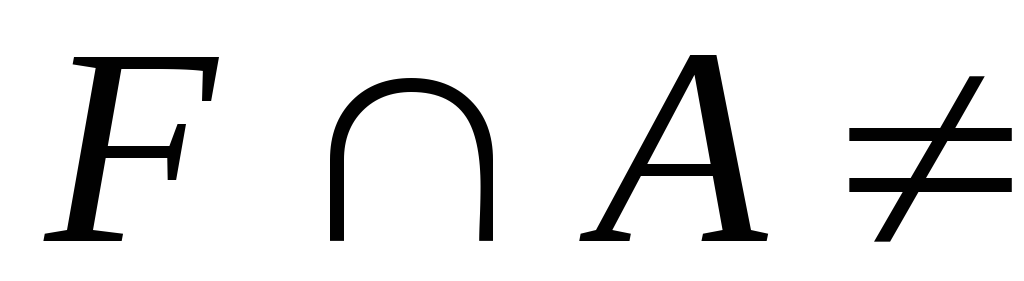
 ,
,

 ,
то
,
то

 .
.З’ясувати, чи будуть гомеоморфними множини точок поверхні двовимірного тору в
 3
та
множина точок сфери в
3
та
множина точок сфери в
 3.
3.
Варіант 9
Нехай на множині
 задані топологічні структури
задані топологічні структури і
і та
та .
З’ясувати, чи випливає із зв’язності
.
З’ясувати, чи випливає із зв’язності зв’язність простору
зв’язність простору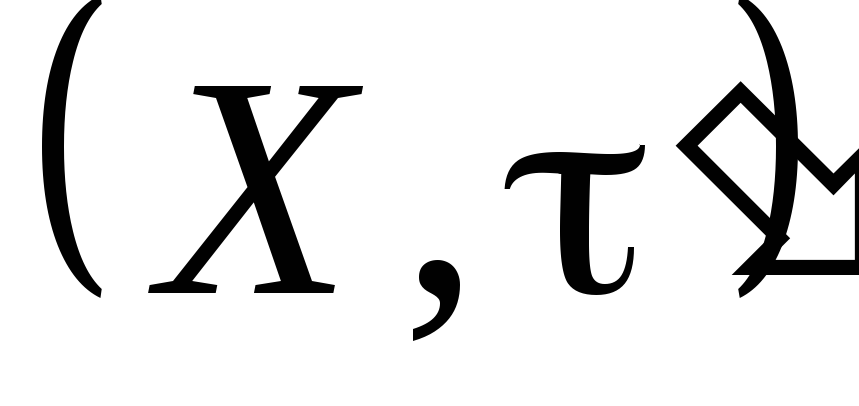 .
А навпаки?
.
А навпаки?Нехай множини
 і
і зв’язні та
зв’язні та
 .
Довести, що
.
Довести, що –
зв’язна множина.
–
зв’язна множина.Довести, що простір
 незв’язний тоді і тільки тоді, коли
існує неперервна сюр’єкція
незв’язний тоді і тільки тоді, коли
існує неперервна сюр’єкція
 (
( – коло одиничного радіуса з центром в
0 простору
– коло одиничного радіуса з центром в
0 простору
 1
).
1
).Визначити, чи будуть гомеоморфними інтервал в
 та коло в
та коло в 2.
2.
Компактні топологічні простори
Варіант 1
Довести, що в кожному нескінченному компактному просторі існує зчисленна незамкнена множина.
Довести, що перетин будь-якої сім’ї компактних підмножин гаусдорфового простору буде компактним.
Довести, що якщо

 - неперервна функція, то
- неперервна функція, то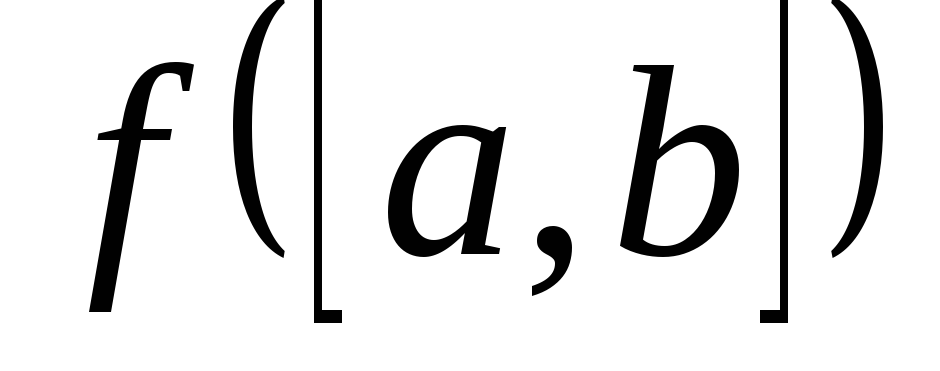 – замкнений інтервал або точка.
– замкнений інтервал або точка.
Варіант 2
Нехай
 –
нескінченна множина, яка наділена
топологією скінченних доповнень.
Довести, що будь-яка підмножина цього
простору буде компактною.
–
нескінченна множина, яка наділена
топологією скінченних доповнень.
Довести, що будь-яка підмножина цього
простору буде компактною.Довести, що перетин спадної послідовності компактних не порожніх зв’язних підмножин гаусдорфового простору
 також буде не порожньою зв’язною
множиною.
також буде не порожньою зв’язною
множиною.Нехай
 – метричний простір, а
– метричний простір, а – його компактний підпростір. Довести,
що для
– його компактний підпростір. Довести,
що для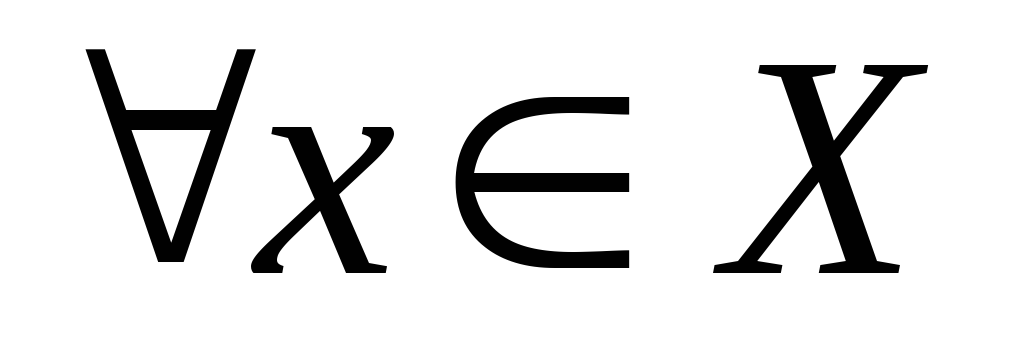 існує
існує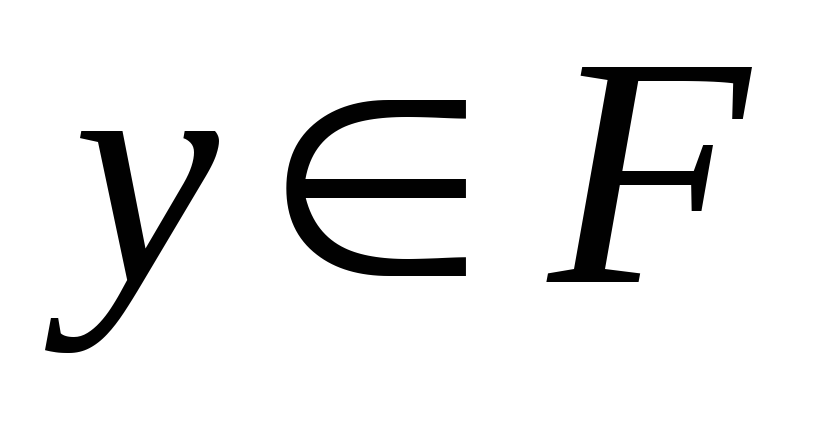 ,
такий що
,
такий що .
.
Варіант 3
Довести, що якщо
 – замкнена множина, а
– замкнена множина, а – неперетинна з ним компактна підмножина
метричного простору, то
– неперетинна з ним компактна підмножина
метричного простору, то
 .
.Нехай


 ,
де
,
де – множина дійсних чисел, а
– множина дійсних чисел, а
 .
Введемо на множині
.
Введемо на множині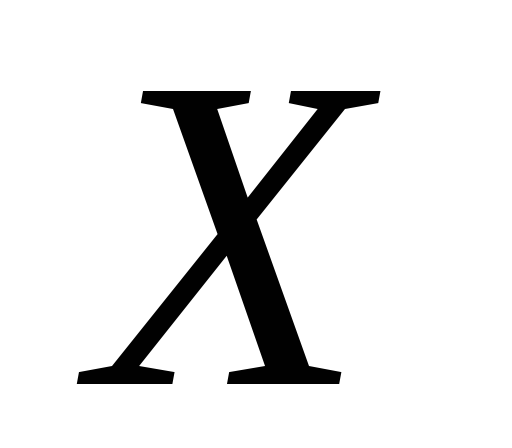 топологію, у якій відкритими множинами
будуть об’єднання відкритих множин,
які належать
топологію, у якій відкритими множинами
будуть об’єднання відкритих множин,
які належать з множиною
з множиною .
Перевірити аксіоми відкритих множин.
Довести, що множина
.
Перевірити аксіоми відкритих множин.
Довести, що множина – компактна, а
– компактна, а – не компактна.
– не компактна.З’ясувати, які з наведених множин будуть компактними:
а)
![]() в
в![]() ;
;
б)
![]() +=
+=![]()
![]() |
|
![]() в
в![]() ;
;
в) коло
в
![]() 2;
2;
г) куля
в
![]() 2;
2;
д)
однополий гіперболоїд в
![]() 3.
3.
Варіант 4
Нехай
 і
і –
компактні підмножини метричного
простору. Довести, що існують такі точки
–
компактні підмножини метричного
простору. Довести, що існують такі точки і
і ,
що
,
що .
.Довести, що замкнена підмножина фінально-компактного простору буде фінально-компактною
Довести, що графік функції

 компактний у
компактний у 2
тоді і тільки тоді, коли
2
тоді і тільки тоді, коли
 – неперервна функція.
– неперервна функція.
Варіант 5
Нехай
 – довільна не порожня множина, а
– довільна не порожня множина, а – компактна підмножина метричного
простору. Довести, що існує така точка
– компактна підмножина метричного
простору. Довести, що існує така точка ,
що
,
що .
.Довести, що компактний гаусдорфів простір метризований тоді, коли він має зчисленну базу.
Навести приклад розривної функції

 ,
графік якої замкнений, але некомпактний.
,
графік якої замкнений, але некомпактний.
Варіант 6
Довести, що перетин будь-якої сім’ї замкнених компактних множин буде компактною множиною.
Нехай
 –
топологічний простір, а
–
топологічний простір, а
 –
компактний топологічний простір.
Довести, що відображення
–
компактний топологічний простір.
Довести, що відображення
 буде замкненим неперервним відображенням.
буде замкненим неперервним відображенням.Довести, що властивість зчисленної компактності спадкується при переході до замкненого підпростору.
Варіант 7
Довести, що компактний простір з дискретною топологією – скінченний.
Довести, що топологічний простір компактний тоді і тільки тоді, коли кожне покриття цього простору елементами деякої бази містить скінченне під покриття.
Довести, що неперервний образ зчисленно-компактної множини топологічного простору також зчисленно-компактний.
Варіант 8
Довести, що неперервний образ фінально-компактної множини топологічного простору теж фінально-компактний.
Довести, що для будь-якої неперервної додатно-визначеної функції
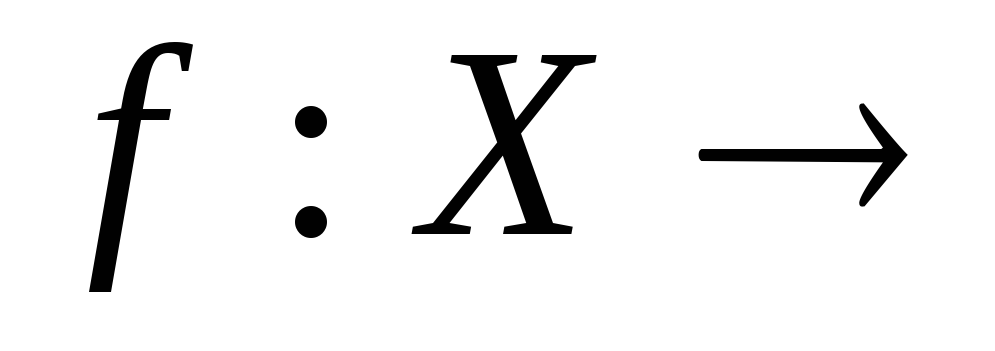
 на компактному просторі
на компактному просторі існує
існує таке, що
таке, що для
для .
.З’ясувати, чи будуть компактними дискретні та тривіальні топологічні простори.
Варіант 9
Нехай для

 – довільна сім’я
компактних підмножин у гаусдорфовому
просторі така, що перетин будь-якого
скінченного числа елементів з
– довільна сім’я
компактних підмножин у гаусдорфовому
просторі така, що перетин будь-якого
скінченного числа елементів з
 – зв’язний. Довести, що множина
– зв’язний. Довести, що множина – зв’язна.
– зв’язна.Довести, що будь-який простір компактного метризованого простору – сепарабельним.
Нехай


 ,
де
,
де – множина дійсних чисел,
– множина дійсних чисел,

 ,
,

 ,
,
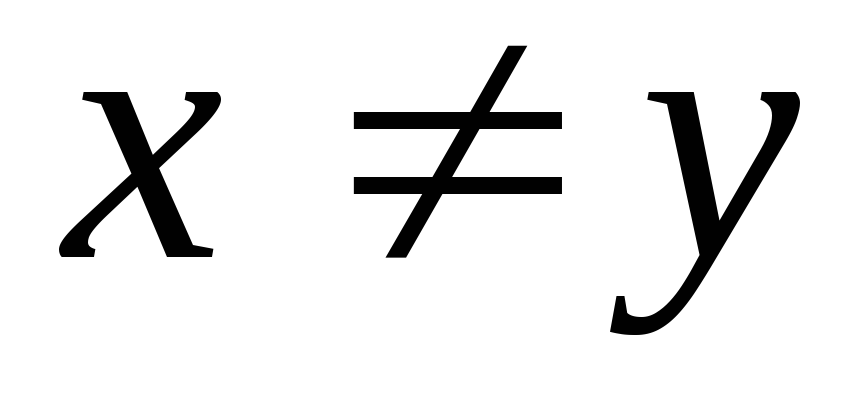 .
Введемо в
.
Введемо в
 топологію, у якій множина відкрита тоді
і тільки тоді, коли вона або відкрита
в
топологію, у якій множина відкрита тоді
і тільки тоді, коли вона або відкрита
в ,
або доповнення до неї скінченне.
Перевірити аксіоми відкритих множин.
Довести, що множини
,
або доповнення до неї скінченне.
Перевірити аксіоми відкритих множин.
Довести, що множини


 і
і


 – компактні в
– компактні в але їх перетин – не компактний.
але їх перетин – не компактний.
