AGLA

Ця система має єдиний розв’язок x0 = 0, y0 = −2. Перенесемо початок координат в центр кривої (x0, y0) (точку O0(0, −2)) за допомогою

перетворення	( y = y + y0			( y = y 2.
	x = x + x0	,		x = x,
	b			b −
	y в рiвняння кривої:
Пiдставимо вирази для x,b				b

5xb2 − 2xb (yb − 2) + 5 (yb − 2)2 − 4xb + 20 (yb − 2) + 8 = 0.

Розкривши дужки i звiвши подiбнi доданки, отримаємо рiвняння γ в новiй системi координат xOb 0yb :

5xb2 − 2xbyb + 5yb2 − 12 = 0.

(1)

Зауважимо, що отримане рiвняння не мiстить лiнiйних доданкiв, а коефiцiєнти при доданках в других степенях не змiнилися. Подальшого спрощення рiвняння (а саме, позбавлення вiд доданку вигляду xbyb) можна досягти, зробивши поворот системи координат на деякий кут α :

(

xb = xe cos α − yesin α, yb = xe sin α + yecos α.

Пiдставимо вирази для x,b yb в рiвняння (1) :

5 (x cos α − y sin α)2 − 2 (x cos α − y sin α) (x sin α + y cos α) +
e	e +5 ( sin			e+			cos e −	e	e
		x		α		y	α)2	12 = 0.	(2)
Розкривши дужки,		знайдемо коефiцiєнт при
		e				e
		xy : −2			cos2 α − sin2 α
i виберемо кут α так,		щоб цей коефiцiєнт дорiвнював							0 :
		ee	cos2 α − sin2 α = 0.
		−2

121

	y
	^	~
		x
	y		x
~
y
	F
	1
	α		^
			x
F	O
2

Наприклад, кут α = π/4 задовольняє це рiвняння. Враховуючи, що

π

π

1

cos

= sin

=

√

, спростимо (2) :

4

4

2

5

(x − y)2

− (x − y) (x + y) +

5

(x + y)2

− 12 = 0.

2

2

Розкривши e

e

e e e

e

e e

дужки i звiвши рiвняння до канонiчного виду, отримаємо

x2

y2

e

+

e

= 1.

3

2

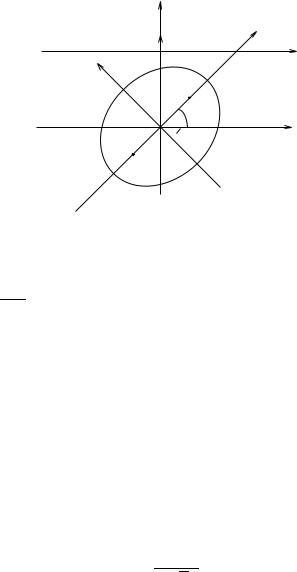
Це рiвняння кривої γ в системi координат xOe 0y,e яка пов’язана з xOy такими спiввiдношеннями:

	x =	x√−2			y	,
		e	+ e
	y =	x		y		−	2.
	e√2e
З вигляду канонiчного	рiвняння робимо висновок, що крива γ є елiпсом.

б) Для того, щоб визначити тип заданої кривої (позначимо її γ), скористаємось результатом задачi 8.100. Знайдемо

δ =		B C		=		2	3		= −4 < 0.
		A B				0	2

122

Так як δ < 0, то робимо висновок, що крива γ є кривою гiперболiчного типу (гiперболою або парою перетинних прямих).

Знайдемо координати центра γ, для цього скористаємось результатом задачi 8.97, з якої випливає, що координати центра кривої другого порядку задовольняють таку систему лiнiйних рiвнянь:

( Bx0	+ Cy0	+ E = 0		( 2x0	+ 3y0 + 6 = 0.
Ax0	+ By0	+ D = 0,		2y0	+ 8 = 0,

Ця система має єдиний розв’язок x0 = 3, y0 = −4. Перенесемо початок координат в центр кривої (x0, y0) (точку O0(3, −4)) за допомогою

перетворення	( y = y + y0		( y = y 4.
	x = x + x0,		x = x + 3,
	b		b −
	y в рiвняння кривої:
Пiдставимо вирази для x,b			b

4 (xb + 3) (yb − 4) + 3 (yb − 4)2 + 16 (xb + 3) + 12 (yb − 4) − 36 = 0.

Розкривши дужки i звiвши подiбнi доданки, отримаємо рiвняння γ в новiй системi координат xOb 0yb :

4xbyb + 3yb2 − 36 = 0.

(3)

Зауважимо, що отримане рiвняння не мiстить лiнiйних доданкiв, а коефiцiєнти при доданках в других степенях не змiнилися. Подальшого спрощення рiвняння (а саме, позбавлення вiд доданку вигляду xbyb) можна

досягти, зробивши поворот системи координат на деякий кут α :

(

xb = xe cos α − yesin α, yb = xe sin α + yecos α.

Пiдставимо вирази для x,b yb в рiвняння (3) :

4 (xe cos α − ye sin α) (xe sin α + yecos α) + 3 (xe sin α + yecos α)2 −36 = 0. (4)

Розкривши дужки, знайдемо коефiцiєнт при

xy : 4	cos2	α − sin2	α	+ 6 sin α cos α
ee

123

i виберемо кут α так, щоб цей коефiцiєнт дорiвнював 0 :

4	cos2 α − sin2 α + 6 sin α cos α = 0.	2
Подiлимо праву i лiву частину цього рiвняння на 2 cos α :
	2 tg2 α − 3 tg α − 2 = 0.

Отримане квадратне рiвняння має два розв’язки tg α = −1/2 або tg α = 2. Виберемо другий розв’язок (виключно з мiркувань простiшого значення) i, скориставшись тригонометричними формулами, знайдемо

					1							1							tg α			2
cos α =										=			√		,	sin α =						=	√		,
			p1 + tg			2												p1 + tg		2
							π				π	5									α	5
							α
вважаючи, що α					−			,					. Пiдставимо отриманi									вирази в (4) i
							2			2
спростимо рiвняння:
4			(xe − 2ye) (2xe + ye) +													3	(2xe + ye)2 − 36 = 0.
5																5

y	^	~
	y
		x
~
y
	F	x
	1
	α	^
		x
	O
F
2

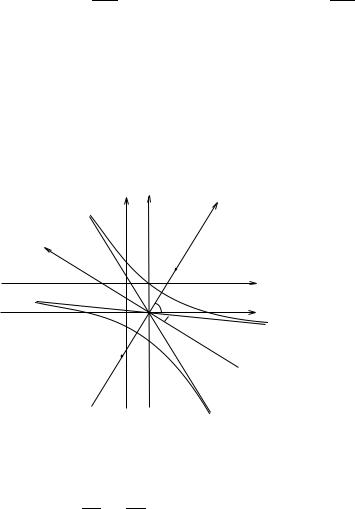
Розкривши дужки i звiвши рiвняння до канонiчного виду, отримаємо

xe2 − ye2 = 1.

9 36

124

Це рiвняння кривої γ в системi координат xOe 0y,e яка пов’язана з xOy такими спiввiдношеннями:

	x =	x	√−5		+ 3,
			2y
		e	e
	y =	2x + y				4.
		e 5 e			−
			√
З вигляду канонiчного	рiвняння робимо висновок, що крива γ є гiпербо-

лою.

в) Для того, щоб визначити тип заданої кривої (позначимо її γ), скористаємось результатом задачi 8.100. Знайдемо

δ =		B C		=		−	3	−1		= 0.
		A B					9	3

Так як δ = 0, то робимо висновок, що крива γ є кривою параболiчного типу (параболою, парою паралельних прямих, парою уявних паралельних прямих або парою паралельних прямих, якi збiгаються).

В даному випадку крива γ не має центра, тому спрощення рiвняння (а саме, позбавлення вiд доданку вигляду xbyb) почнемо з повороту системи

координат на деякий кут α :

(

x = xb cos α − ybsin α, y = xb sin α + ybcos α.

Пiдставимо вирази для x,b yb в задане рiвняння γ :

9 (xb cos α − ybsin α)2 − 6 (xb cos α − ybsin α) (xb sin α + ybcos α) +

+ (xb sin α + ybcos α)2 −10 (xb cos α − ybsin α)+10 (xb sin α + yb cos α)−10 = 0

(5)

Розкривши дужки, знайдемо коефiцiєнт при
ee
xy : −16 cos α sin α − 6	cos2 α − sin2	α

i виберемо кут α так, щоб цей коефiцiєнт дорiвнював 0 :

−16 sin α cos α − 6 cos2 α − sin2 α = 0.

125

126

Подiлимо праву i лiву частину цього рiвняння на 2 cos2 α : 3 tg2 α − 8 tg α − 3 = 0.

Отримане квадратне рiвняння має два розв’язки tg α = −1/3 або tg α = 3. Виберемо другий розв’язок (виключно з мiркувань простiшого значення) i, скориставшись тригонометричними формулами, знайдемо

cos α =

1

=

1

,

sin α =

tg α

=

3

,

√

√

p1 + tg

2

p1 + tg

2

α

α

10

10

π

π

вважаючи,

що

α

−

,

. Пiдставимо

отриманi

вирази

в (5) i

2

2

спростимо рiвняння:

9

(x − 3y)2

6

1

(3x + y)2 −

10

−

(x − 3y) (3x + y) +

√

(x − 3y) +

10

10

10

10

b

b

b

10

b

b

b

b

b

b

b

+

√

(3x + y) − 10 = 0.

10

Розкривши дужки i звiвши подiбнi доданки, отримаємо

b

b

y2 +

2

x +

4

y = 1.

√

√

10

10

Видiлимо повний квадрат вiдносно y i зведемо отримане рiвняння до

b

b

b

b

канонiчного виду:

2

2

7

2

y +

√

= −√

x −

√

.

10

10

10

b

b

O0

7

2

Перенесемо

початок

координат

в

точку

√

, −√

(це

10

10

координати в xOy) за допомогою перетворення

b

b

x = x

7

,

− √10

2

y = y + .

e

b

√10

e

b

	y	~
~		^ x
		x
y		O
		F
^
y	α
		x

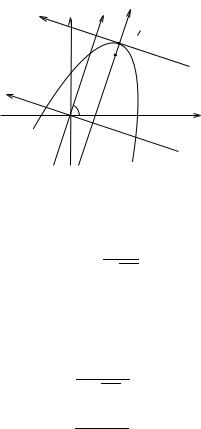
В системi координат xOe 0ye крива γ має канонiчне рiвняння

ye2 = −√2 xe.

10

З вигляду канонiчного рiвняння робимо висновок, що γ є параболою.

Системи координат xO0y i xOy пов’язанi мiж собою такими спiввiдно-
шеннями:	e e	x	3y				13
	x =	√−10				+		,
							10
		3x + y					19
		e		e
	y =			e		+ .
		√
							10
		e	10

Задачi для самостiйної роботи

Коло

8.1. Скласти рiвняння кола, якщо

а) центр кола збiгається з початком координат, а його радiус дорiвнює

3;

б) центр кола знаходиться в точцi C(2, −3), а його радiус дорiвнює 7;

в) коло проходить через початок координат, а його центр знаходиться в точцi C(6, −8);

г) коло проходить через точку M (2, 6), а його центр знаходиться в точцi C(−1, 2);

127

д) точки M1(3, 2) i M2(−1, 6) є кiнцями одного з дiаметрiв кола;

е) центр кола збiгається з початком координат, а пряма 3x−4y+20 = 0 є дотичною до кола;

є) центр кола знаходиться в точцi C(1, −1), а пряма 5x − 12y + 9 = 0 є дотичною до кола;

ж) коло проходить через точки M1(3, 1) i M2(−1, 3), а його центр лежить на прямiй 3x − y − 2 = 0;

з) коло проходить через три точки M1(1, 1), M2(1, −1) i M3(2, 0);

и) коло проходить через три точки M1(−1, 5), M2(−2, −2) i M3(5, 5);

i)центр кола знаходиться в точцi C(3, −1), а також вiдомо, що коло вiдсiкає на прямiй 2x − 5y + 18 = 0 хорду, довжина якої дорiвнює 6.

8.2. За якої необхiдної i достатньої умови рiвняння

Ax2 + Ay2 + 2Bx + 2Cy + D = 0, A =6 0

визначає коло? вироджене коло? уявне коло? У першому випадку виразити радiус и координати центра кола через коефiцiєнти рiвняння.

8.3. Якi з наступних рiвнянь визначають коло? вироджене коло? уявне коло? У першому i другому випадку знайти координати центра C i радiус R кола:

а) (x − 5)2 + (y + 2)2 = 25;					е) x2	+ y2	− 2x + 4y + 14 = 0;
б) (x + 2)2 + y2				= 64;
в) (x − 5)2 + (y + 2)2 = 0;					є) x2 + y2 − 2x + 4y + 5 = 0;
г) x	2	+ (y − 5)	2	= 5;	ж) x2 + y2 + x = 0;
д) x2 + y2 − 2x + 4y − 20 = 0;					з) x2 + y2 + 6x − 4y + 14 = 0;

128

и) x2 + y2 + y = 0;

ї) 7x2 + 7y2 − 2x − 7y − 1 = 0.

i) 2x2 + 2y2 − 12x + y + 3 = 0;

8.4.Скласти рiвняння кола радiуса R, яке дотикається осей координат.

8.5.Скласти рiвняння кола, якщо точки M1 (x1, y1) i M2 (x2, y2) є кiнцями одного з його дiаметрiв.

8.6. Скласти рiвняння кола, що проходить через три точки (xi, yi), i = 1, 2, 3, якi не лежать на однiй прямiй.

8.7.Скласти рiвняння кола, яке проходить через двi точки M1(x1, y1) i M2 (x2, y2) знаючи, що його центр лежить на прямiй Ax + By + C = 0.

8.8.Знайти необхiднi i достатнi умови того, що пряма

Ax + By + C = 0

а) перетинає коло (x − a)2 + (y − b)2 = R2;

б) не перетинає це коло;

в) дотикається цього кола.

Елiпс

8.9. Знайти велику, малу пiвосi, координати фокусiв, ексцентриситет, рiвняння директрис наступних елiпсiв i зобразити їх на рисунку:

а) 9x2 + 25y2	= 225;	в) 5x2 + 16y2	= 80;
б) 25x2 + 9y2	= 225;	г) 16x2 + 5y2	= 80.

8.10. Знайти довжини фокальних радiусiв точки M для кожного з елiпсiв задачi 8.9, якщо:

129

а) M

−3 , 2√5

;

в) M 2, − 2

!

;

5

√

15

б) M 5 , 3 ;

г) M −

8

, −

2

! .

√

√

12

265

11

8.11. Скласти рiвняння елiпса, фокуси якого знаходяться на осi абсцис симетрично вiдносно початку координат, якщо:

а) його осi дорiвнюють 12 та 4;

б) велика вiсь дорiвнює 10, а вiдстань мiж фокусами 8;

в) мала вiсь дорiвнює 24, а вiдстань мiж фокусами 10;

г) вiдстань мiж фокусами дорiвнює 6, а ексцентриситет 3/5;

д) велика вiсь дорiвнює 20, а ексцентриситет 3/5;

е) мала вiсь дорiвнює 10, а ексцентриситет 12/13;

є) вiдстань мiж директрисами дорiвнює 5, а вiдстань мiж фокусами 4;

ж) велика вiсь дорiвнює 8, а вiдстань мiж директрисами 16;

з) мала вiсь дорiвнює 6, а вiдстань мiж директрисами 13;

и) вiдстань мiж директрисами дорiвнює 32, а ексцентриситет 1/2.

8.12. Скласти рiвняння елiпса, фокуси якого знаходяться на осi ординат симетрично вiдносно початку координат, якщо:

а) осi дорiвнюють 14 i 6;

б) велика вiсь дорiвнює 10, а вiдстань мiж фокусами 6;

в) мала вiсь дорiвнює 6, а вiдстань мiж фокусами 16;

г) вiдстань мiж фокусами дорiвнює 24, а ексцентриситет 12/13;

130