AGLA

Київський нацiональний унiверситет iменi Тараса Шевченка

Л.Л. ЗАЙЦЕВА А.В. НЕТРЕБА

АНАЛIТИЧНА ГЕОМЕТРIЯ В ПРИКЛАДАХ I ЗАДАЧАХ

Видавничо–полiграфiчний центр “Київський унiверситет“

2008

Зайцева Л.Л., Нетреба А.В.

Збiрник задач з аналiтичної геометрiї. – К.: Видавничо–полiграфiчний центр “Київський унiверситет”, 2008. – 200 с.

Рецензенти: д-р фiз.-мат. наук, Пилипенко А.Ю. канд. фiз.-мат. наук, доц. Єфiменко С.В.

Наведено завдання для практичних занять з аналiтичної геометрiї. Посiбник мiстить завдання рiзного рiвня складностi для аудиторної та самостiйної роботи. Наведено приклади розв’язання типових задач.

Для студентiв, викладачiв фiзико-математематичних спецiальностей

Рекомендовано до друку вченою радою радiофiзичного факультету Київського нацiонального унiверситету iменi Тараса Шевченка (протокол № 13 вiд 19 травня 2008 року)

Змiст

Передмова

4

1Визначники II i III порядкiв, їх властивостi. Метод Крамера розв’язання систем лiнiйних рiвнянь II та III поряд-

	кiв	5
2	Поняття вектора. Лiнiйнi операцiї над
	векторами	20
3	Скалярний, векторний, мiшаний добутки векторiв	26
4	Рiвняння прямої на площинi, площини i прямої в просторi
	у векторнiй формi	45
5	Загальне рiвняння прямої на площинi. Загальне рiвняння
	площини в просторi.	54
6	Рiвняння прямої в просторi. Взаємне розташування пря-
	мої i площини	67
7	Нормальне рiвняння прямої на площинi. Нормальне рiв-
	няння площини в просторi	81
8	Кривi другого порядку	103
9	Поверхнi другого порядку	158
Лiтература		224

3

Передмова

В посiбнику запропоновано задачi для забезпечення навчальним матерiалом практичнi заняття з курсу "Аналiтична геометрiя". Структура посiбника повнiстю вiдповiдає послiдовностi практичних занять першої частини курсу "Аналiтична геометрiя та лiнiйна алгебра", яка читається на фiзичному та радiофiзичному факультетах Київського нацiонального унiверситету iменi Тараса Шевченка. Посiбник мiстить як простi задачi, спрямованi на розкриття властивостей геометричних об’єктiв i вмiння застосовувати основнi формули аналiтичної геометрiї, так i задачi пiдвищеної складностi, призначенi для поглибленого вивчення навчальної дисциплiни та органiзацiї самостiйної роботи студентiв. При складаннi посiбника автори спирались на власний багаторiчний досвiд викладання на фiзичному i радiофiзичному факультетах Київського нацiонального унiверситету iменi Тараса Шевченка. Деяка частина запропонованих задач запозичена з класичних збiрникiв [3, 6, 7, 10]. Разом з тим, посiбник мiстить значну кiлькiсть оригiнального матерiалу.

На початку кожного роздiлу коротко перераховуються основнi теоретичнi поняття, якими повинен володiти студент для того, щоб приступати до розв’язання задач. Ознайомитись з теоретичним матерiалом читач може в [2, 5, 9] (основна рекомендована лiтература) або, бiльш детально, в [1, 4, 8]. З метою полегшення самостiйного вивчення матерiалу у кожному роздiлi детально розiбранi приклади розв’язання типових задач, переважну бiльшiсть яких проiлюстровано рисунками.

Посiбник орiєнтований на роботу викладачiв та студентiв, якi викладають чи вивчають аналiтичну геометрiю в обсязi, передбаченому навчальними програмами фiзичних, математичних та технiчних спецiальностей унiверситетiв та iнших вищих навчальних закладiв.

4

1Визначники II i III порядкiв, їх властивостi. Метод Крамера розв’язання систем лiнiйних рiвнянь II та III порядкiв

Вцьому роздiлi використовуються такi поняття та результати.

1.Методи обчислення визначникiв II та III порядкiв. Властивостi визначникiв.

2.Системи лiнiйних рiвнянь II та III порядкiв. Метод Крамера розв’язання систем лiнiйних рiвнянь II та III порядкiв. Необхiдна i достатня умова iснування єдиного розв’язку системи лiнiйних рiвнянь II та III порядкiв.

3.Обчислення визначникiв старших порядкiв методом зведення до визначникiв менших порядкiв. Формула Лапласа.

Приклади розв’язання задач

Приклад 1.1. Oбчислити визначники другого порядку:

	b1	b2		;		4	−5	.
	a1	a2				1	−

Розв’язання. Знайдемо визначники, користуючись правилами обчис-

лення визначникiв:						4	−5		= 1 · (−5) − (−3) · 4 = 7.
	b1	b2		= a1b2 − a2b1;
	a1	a2				1	−

Приклад 1.2. Oбчислити визначники третього порядку:

b1

b2

b3

;

4

11

−2

.

c c c

5 −

8

−7

a1

a2

a3

1

9

3

1

2

3

−

Розв’язання. Знайдемо перший визначник:

b1

b2

b3

= a1b2c3 + a2b3c1

+ a3b1c2

−

a3b2c1

−

a1b3c2

−

a2b1c3.

c

c

c

a1

a2

a3

1

2

3

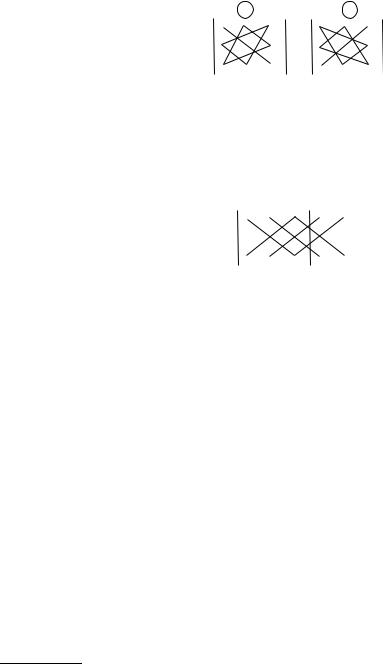
Для запам’ятовування цiєї вiдповiдi зручно використовувати один з наступних методiв:

5

	+	a3	-
a1 a2			a1 a2	a3
b1	b2	b3	b1 b2	b3	;
c1	c2	c3	c1 c2	c3

а) метод "зiрочка":

б) метод "допомiжних стовпчикiв":

+	+	+
a1	a2	a3 a1		a2	;
b1	b2	b3	b1 b2
c1 c2		c3	c1	c2
-	-	-

в) метод розкладу по довiльному рядку або стовпчику (покажемо на

прикладi першого рядка):

b1

b2

b3

= a1

c2

c3

−

a2

c1

c3

+ a3

c1

c2 .

c c c

2

3

1

3

1

2

a1

a2

a3

b

b

b

b

b

b

1

2

3

Знайдемо другий визначник:

4

−

11

−2

= 1

·

(

−

11)

·

(

−

7) + 9

·

(

−

2)

·

5 + 4

·

8

·

(

−

3)

−

5

8

−7

1

9

3

−

−(−3) ·

−

11)

·

5

−

(

−

2)

·

8

·

1

−

9

·

4

·

(

−

7) =

−

6

(

Приклад 1.3. Користуючись властивостями визначникiв, обчислити:

	5	1	−5		;		b + c a	1	.
	1	−2	−2				c + a b	1
	4	1	4				a + b c	1
			−

6

Розв’язання. Обчислимо перший визначник, скориставшись наступними перетвореннями: додамо до другого рядка перший; додамо до третього рядка перший, помножений на (−2). В результатi отримаємо:

		5	1	−5		=			9	0	−9	.
		1	−2	−2					7	0	−6
		4	1	4					4	1	4
				−				−
Далi розкладемо	визначник по елементах другого стовпчика, пiсля чого

винесемо коефiцiєнт 9 з першого рядка i обчислимо отриманий визначник другого порядку:

		9	0	−9		=	−			7	−6		=	−	9			7	−6		=
		7	0	−6
		4	1	4					−	9	9						−	1	1
	−
						= −9 (6 − 7) = 9.

Обчислимо другий визначник, скориставшись наступними перетвореннями: додамо до другого i до третього рядкiв перший, помножений

на (−1). В результатi отримаємо:									.
		b + c a 1		=		c a a c 0
		c + a b 1				c − b b	− c 0
		a + b c 1				a + b	c	1
						−	−
Далi розкладемо	визначник по елементах третього стовпчика, пiсля чого

винесемо коефiцiєнти (c − a) з першого i (c − b) з другого рядка, пiсля чого обчислимо отриманий визначник другого порядку:

	c a a c 0			=		c	− b b − c				=
	c − b b	− c 0
	a + b	c 1				c	−		−
	−	−
						1	1		= 0.
	= (c − a) (c − b)					1	−1
							−

7

Приклад 1.4. Oбчислити визначники четвертого порядку:

		7	0	−5			−4			;		−3		7	−2		−5	.
		−5	0		5			7				−6		−7		5	4
		3	2		1			5					4	0		7	5
		8	1	−	4		−	2					5	2		5	8
				−			−					−			−
		Знайдемо
Розв’язання.						перший визначник. Для спрощення обчислень

розкладемо його по рядку або стовпчику, який мiстить найбiльшу кiлькiсть нулiв, в данiй ситуацiї по другому стовпчику:

										7	0			−5						−4						= 2								(			1)1+2													−5					5						7		+
						−5					0						5					7
										3	2						1					5											· −																		8			−4				−2
																																																			7				5						4
										8	1			−			4			−		2																																−				−
														−						−
																3					1						5																											3							1				5
+0					(					1)2+2						5				−5					−7							+ 0					·			(		−				1)3+2								7				−5				−4							+
			· −													8				−4					−2																												−8								4 2
																				−					−																																	−				−
																		3			−			1			−
+1				(					1)		4+2							7						5										=							2						(												66) =
		·				−																							4								−							·					−		24) + (					−									−			18.
													−5 5																7
																													5
																					−						−
Знайдемо другий визначник.																													Розкладемо його по першому рядку:
				−3							7			−2						−5						= (								4)					(						1)1+1								−7							5		4				+
				−6						−7							5					4
							4				0						7					5									−					· −																		2						5		8
																																																						7						2		5
				−			5				2			−			5					8																																			−
								1)1+2										3					2			5																																3				7				5
+0	·			(	−										−6								5			4				+ (					−			7)								(				1)1+3					−6						−7					4				+
																		5 5 8																									· −															5 2 8
															−					−																																			−
																																			−					3					−				7				2
																			5)									1+4																											=
												+ (					−						( 1)																	6 7 5
																					· −																			5									2				5
										=					4			(			741)									7					−																−
												−															−						·																·						−
																	· −																																								35.
																																		567 + 5																194 =

8

Приклад 1.5. Розв’язати системи лiнiйних рiвнянь:
		(			7x − 9y = 2,												6;						67x− 76y−+ z =																−3,
						2x + 3y =																			x				−		y		2z =						−	3,
					−										−										x + y + 2z = 1.
Розв’язання.																					лiнiйних рiвнянь маємо:
			Для першої системи																						= 3 6= 0,
													=					−	2		−3
																			7				9
звiдки робимо висновок, що система має єдиний розв’язок. Знайдемо
його, для цього обчислимо ще два визначника:																																			6			= −38.
1		=					−	6		−3				= −48,										2 =						−		2	−
								2		9																						7			2
Таким чином,
										1																				2			38
							x =						= −16;											y =							= −						.
																																			3
Для другої системи лiнiйних рiвнянь маємо:
										=				7				−6			−1				=		−			13 = 0,
														1				−1					2									6
														6				7					2
													що система має єдиний розв’язок. Знайдемо
звiдки робимо висновок,
його, для цього обчислимо ще три визначника:																																								=
1 =			−3				−6				−1				=			−		16,					2	=					7		−3				−1				−	23,
			−1				−1			2																					1		−1 2
					3			7		2																					6		3						2
																		6			7				3
										3 =								7			−6			−3					= 13.
																		1			−1				1
Таким чином,
	x =				1			16													2				23												3
							=					;				y =							=				;					z =							= −1.
									13																13

9

Приклад 1.6. Довести, що однорiдна система лiнiйних рiвнянь третього

порядку

b1x + b2y + b3z = 0,

a1x + a2y + a3z = 0,

c1x + c2y + c3z = 0

має єдиний нульовий

розв’язок тодi i тiльки тодi, коли визначник систе-

ми

=

b1

b2

b3

= 0

c

c

c

6

a1

a2

a3

1

2

3

Розв’язання.

З теореми

Крамера вiдомо, що система лiнiйних рiвнянь

6= 0. Тому залишилось

має єдиний розв’язок тодi i тiльки тодi, коли

перевiрити, що цей розв’язок буде нульовим. Дiйсно,

1 =

0 b2

b3

= 0,

2 =

b1

0 b3

= 0,

0

c

c

c

0

c

0

a2

a3

a1

0

a3

2

3

1

3

=

a1

a2

0

3

b1

b2

0

,

c

c

0

1

2

звiдки

x =

1

= 0,

y =

2

= 0,

z =

3

= 0.

Твердження доведено.

Приклад 1.7. Дослiдити, при яких значеннях параметрiв система лiнiйних рiвнянь має єдиний розв’язок, несумiсна, має безлiч розв’язкiв? У випадках, коли система сумiсна, вказати всi розв’язки системи.

а)	( ax + 9y = 3b;	б)		8x + 7y + az = 5,
	2x − 3y = b + 1,		−4x + 3y − z = b,
			−	4x		−
					−	2y + 6z = 1;

10