AGLA

Приклади розв’язання задач

Приклад 2.1. Нехай
	~	~
~a = {1, 2, 0}, b = {−2, −1, 2}, ~c = {1, 1, −1}, d = {3, 2, 1}.
~		~

Знайти координати вектора 3~a + 2b − 3~c + d.

Розв’язання. Оскiльки кожна координата лiнiйної комбiнацiї векторiв є такою ж самою лiнiйною комбiнацiєю вiдповiдних координат цих век-

торiв, то
~	~
3~a + 2b − 3~c + d = {3 · 1 + 2 · (−2) − 3 · 1 + 3,

3 · 2 + 2 · (−1) − 3 · 1 + 2, 3 · 0 + 2 · 2 − 3 · (−1) + 1} = {−1, 3, 8}.

Приклад 2.2. В просторi задано вектор ~a довжиною 4. Знайти координати вектора ~a, якщо вiдомо, що кут мiж ~a i першим координатним вектором дорiвнює 2π/3, кут мiж ~a i другим координатним вектором дорiвнює π/4 (базис є ортонормованим).

Розв’язання. Нехай ϕ1, ϕ2, ϕ3 це кути, якi утворює вектор ~a з коор-

динатними векторами ~e1, ~e2, ~e3 вiдповiдно. Вiдомо, що cos ϕ1 = −1/2,

√

cos ϕ2 = 1/ 2. Тодi

q

cos ϕ3 = ± 1 − cos ϕ21 − cos ϕ22 = ±1/2,

n √ o

~a = {|~a| cos ϕ1, |~a| cos ϕ2, |~a| cos ϕ3} = 2, ±2 2, ±2 .

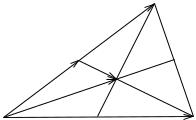
Приклад 2.3. У трикутнику ABC точка M середина вiдрiзку AB,

точка O це точка перетину медiан. Приймаючи за базиснi вектори

~a =

−→

~

=

−→

~

=

−−→

m~ =

AB i b

AC, знайти в цьому базисi координати векторiв k

AM ,

−→

= −−→

AO i ~n

M O.

~ ~

Розв’язання. Зобразимо на рисунку вектори ~a, b, k, m,~ ~n.

Тодi

2 ~a,

~n = 3

−−→ = 3

b − k =

b −

2~a =

3 b −

k =

3

6

~a,

~

1

1

M C

1

~ ~

1

~

1

1

~

1

21

															B
								a
					M				n		O
			k
						m
	A								b							C
~				1			1	~					1			1			1	~
m~ = k + ~n =				2	~a +		3		b −			6			~a =	3	~a +		3	b.		в базисi ~a,~b.
Таким чином, ~k =		2 , 0		, m~ =					3 ,		3				, ~n = −6			, 3
		1							1		1					1		1

Приклад 2.4. Нехай
~	~
~a = {1, 2, 3}, b = {2, 1, 1}, ~c = {1, −1, −1}, d = {9, 3, −6}.

~
a) довести, що вектори ~a, b, ~c є базисом у просторi;
~	~

б) знайти координати вектора d в базисi ~a, b, ~c.

Розв’язання. а) Три вектори є базисом у просторi тодi i тiльки тодi,

~	~
коли вони лiнiйно незалежнi. Це означає, що рiвнiсть α~a + βb + γ~c = 0
повинна виконуватись тодi i тiльки тодi, коли α = β = γ	= 0.

Перевiримо це, записавши дану рiвнiсть покоординатно (якщо нуль-

~

вектор є лiнiйною комбiнацiєю векторiв ~a, b, ~c, тодi кожна координата нуль-вектора є такою ж самою лiнiйною комбiнацiєю вiдповiдних коор-

~
динат векторiв ~a, b, ~c):
		α + 2β + γ = 0
		2α + β − γ = 0
		3α + β	−	γ = 0

Для того, щоб дана система лiнiйних рiвнянь мала єдиний нульовий розв’язок необхiдно i достатньо, щоб визначник системи не дорiвнював

22

нулю (див. приклад 1.6). Дiйсно,

1

2

1

=

2

1 1

=

−

3 = 0.

3

1

−1

6

−

~

x, y, z

~

~

x~a

~

z~c. Це

б) Нехай d

=

в базисi ~a, b, ~c, тобто d

=

+

yb

+

{

}

~

означає, що кожна координата вектора d є такою ж самою лiнiйною

~

комбiнацiєю вiдповiдних координат векторiв ~a, b, ~c. Запишемо це:

x + 2y + z = 9

2x + y − z = 33x + y − z = −6

~

Ця система має єдиний (єдинiсть випливає з того, що вектори ~a, b, ~c є базисом в R3) розв’язок x = −9, y = 13, z = −8.

Задачi для самостiйної роботи

~ ~

2.1. Нехай ~a = {−1, 2, 3}, b = {1, 0 − 1}, ~c = {−1, 1, 1}, d = {4, 2, 0}.

Знайти координати вектора

~ ~

а) 2~a − b − 3~c + d;

~ ~

б) 3d − 5b − ~a − ~c;

~	~
в) 3(~a + b) − 4~c − d;
~	~

г) 3(~c − ~a) − 5(b − d).

2.2. Нехай кут мiж вектором ~a i першим координатним вектором дорiвнює 3π/4, кут мiж вектором ~a i третiм координатним вектором дорiвнює π/3. Знайти вектор ~a, якщо вiдомо, що його довжина дорiвнює

2.

2.3. Визначити координати вектора, який утворює з координатними

√

осями однаковi кути, якщо його довжина дорiвнює 3.

23

2.4. Перевiрити, що чотири точки A(3, −1, 2), B(1, 2, −1), C(−1, 1, −3), D(3, −5, 3) є вершинами трапецiї.

~

2.5. Визначити, якi з наступних трiйок векторiв ~a, b, ~c будуть лiнiйно залежними. У тому випадку, коли це можливо, представити вектор ~c як

~

лiнiйну комбiнацiю векторiв ~a i b :

а) ~a = {5, 2, 1},	~	~c = {−1, −1, 6};
	b = {−1, 4, 2},
б) ~a = {6, 4, 2},	~	~c = {−3, 6, 3};
	b = {−9, 6, 3},

~

в) ~a = {6, −18, 12}, b = {−8, 24, −16}, ~c = {8, 7, 3}.

~

2.6. Нехай заданi вектори ~a = {1, 5, 3}, b = {6, −4, −2}, ~c = {0, −5, 7},

~ ~

d = {−20, 27, −35}. Пiдiбрати числа α, β i γ так, щоб вектори α~a, βb, γ~c i

~

d утворювали замкнену ламану лiнiю, якщо початок кожного наступного вектора з’єднати з кiнцем попереднього.

~

2.7. Перевiрити, що вектори ~a = {4, 1, −1}, b = {1, 2, −5}, ~c = {−1, 1, 1}

~

утворюють базис у просторi. Знайти в базисi ~a, b, ~c координати векторiв

~	б) m~ = {2, 4, −10}; в) ~n = {0, 3, −4}.
a) l = {4, 4, −5};

~

2.8. З однiєї точки простору вiдкладено три вектора ~a, b, ~c. Довести, що кiнець вектора ~c тодi i тiльки тодi лежить на вiдрiзку, з’єднуючому

~ ~

кiнцi векторiв ~a i b, коли виконується рiвнiсть ~c = α~a + βb, де α ≥ 0, β ≥ 0, α + β = 1. У якому спiввiдношеннi кiнець вектора ~c дiлить цей вiдрiзок?

2.9. Нехай r~1, r~2 радiус-вектори точок A i B. Знайти

a)радiус-вектор r~3 точки M, яка лежить на вiдрiзку AB, якщо |AM | :

|BM | = m : n;

24

б) радiус-вектор r~4 точки N, яка лежить на прямiй AB, ззовнi вiдрiзка

AB, якщо |AN | : |BN | = m : n.

2.10. Задано двi точки A(3, −2) i B(1, 4). Точка M лежить на прямiй AB, причому |AM | = 3|AB|. Знайти координати точки M, якщо

a) точки M i B лежать по один бiк вiд точки A;

б) точки M i B лежать по рiзнi боки вiд точки A.

2.11. Три точки A(x1, y1), B(x2, y2) i C(x3, y3) не лежать на однiй прямiй i є послiдовними вершинами паралелограма. Знайти координати четвертої вершини D цього паралелограма.

2.12.Знаючи радiус-вектори r~1, r~2, r~3, r~4 вершин A, B, D, A1 паралелепiпеда ABCDA1B1C1D1, виразити через них радiус-вектори iнших вершин.

2.13.Довести, що радiус-вектор центра правильного багатокутника є середнiм арифметичним радiус-векторiв його вершин.

2.14.У площинi трикутника ABC знайти точку O таку, що

−→	+	−−→	+	−→	= 0
OA		OB		OC	~.

Чи iснують такi точки зовнi трикутника?

2.15. У паралелограмi ABCD точка K середина вiдрiзка BC i точка

−→

O точка перетину дiагоналей. Приймаючи за базиснi вектори AB i

−−→ −−→ −→ −−→

AD, знайти в цьому базисi координати векторiв BD, CO, KD.

2.16. Точки E i F є серединами сторiн AB i CD чотирикутника ABCD.

Довести, що	−−→ + −−→
−→ = 2
1	BC AD .
EF

25

2.17. Задано правильний шестикутник ABCDEF. Приймаючи за

−→ −→

базиснi вектори AB i AF , знайти в цьому базисi координати векторiв

−−→ −−→ −−→ −→ −−→ −→ −−→

BC, CD, DE, EF , BD, CF , CE.

2.18. В тетраедрi OABC точки K, L, M, N, P, Q середини ребер OA,

OB, OC, AB, AC, BC вiдповiдно, S точка перетину медiан трикутника

−→ −−→ −→

ABC. Приймаючи за базиснi вектори OA, OB i OC, знайти в цьому базисi координати векторiв

−→ −−→ −→ a) AB, BC, AC;

−−→ −→ −−→ −−→ −−→

б) KL, P Q, N C, M P , KQ;

−→ −−→

в) OS, KS.

2.19. Задано паралелепiпед ABCDA1B1C1D1. Приймаючи за початок

−→ −−→ −−→

координат вершину A, а за базиснi вектори AB, AD i AA1, знайти в цьому базисi координати

a) вершин C, B1, C1;

б) точок K i L середин ребер A1B1 i CC1 вiдповiдно;

в) точок M i N перетину дiагоналей граней A1B1C1D1 i ABB1A1 вiдповiдно;

г) точки O перетину дiагоналей паралелепiпеда.

3Скалярний, векторний, мiшаний добутки векторiв

Вцьому роздiлi використовуються такi поняття та результати.

1.Проекцiя вектора на вектор. Скалярний добуток векторiв, властивостi скалярного добутку, скалярний добуток векторiв у координатнiй формi, скалярний добуток векторiв у координатнiй формi в ОНБ, застосування скалярного добутку векторiв для обчислення довжини вектора та кута мiж векторами, критерiй ортогональностi векторiв.

26

2.Права, лiва трiйка векторiв. Векторний добуток векторiв, властивостi векторного добутку, векторний добуток векторiв у координатнiй формi в ОНБ, обчислення площi паралелограма за допомогою векторного добутку.

3.Мiшаний добуток векторiв, властивостi мiшаного добутку, мiшаний добуток векторiв у координатнiй формi в ОНБ, застосування мiшаного добутку векторiв для дослiдження, чи є трiйка векторiв компланарною, правою або лiвою, обчислення об’єму паралелепiпеда або трикутної пiрамiди за допомогою мiшаного добутку.

Приклади розв’язання задач

Приклад 3.1. Нехай
				~
			~a = {1, −1, 2}, b = {−3, 1, 0}, ~c = {−1, 1, 2}.
Знайти
а)	~			~	г)	~
	b( ~a, ~c ) − ~c( ~a, b );					Πp~a−2~c(3~a + 2b );
б)	2		2	~ ~	д)	~
	|~a |		+ |~c |	+ ( ~a, b )( b, ~c );		( ~a − ~c, b − ~c );
в)			~		е)	~
	Πp~c (2~a + b );					( 2~a + ~c, 2b − ~c ).
Розв’язання. а)				Обчислимо скалярнi добутки
			( ~a, ~c ) = 1 · (−1) + (−1) · 1 + 2 · 2 = 2,
				~
			( ~a, b ) = 1 · (−3) + (−1) · 1 + 2 · 0 = −4,
звiдки			~	~	~
			b( ~a, ~c ) − ~c( ~a, b ) = 2b + 4~c = {−10, 6, 8}.
б)	За допомогою скалярного добутку обчислимо довжини векторiв

|~a |2 = ( ~a, ~a ) = 1 · 1 + (−1) · (−1) + 2 · 2 = 6,

|~c |2 = ( ~c, ~c ) = (−1) · (−1) + 1 · 1 + 2 · 2 = 6,

а також, знайдемо

~

( b, ~c ) = (−3) · (−1) + 1 · 1 + 0 · 2 = 4,

27

звiдки

|~a |

2

+ |~c |

2

~

~

+ ( ~a, b )( b, ~c ) = 6 + 6 + (−4) · 4 = −4.

в)

Обчислимо

~

~

2~a + b = {−1, −1, 4},

звiдки

( 2~a + b, ~c ) = −1 · (−1) + (−1) · 1 + 4 · 2 = 8,

~

~

8

( 2~a + b, ~c )

Πp

~c ( 2~a + b ) =

=

√

.

|~c |

г)

Обчислимо

6

~

3~a + 2b = {−3, −1, 6} , ~a − 2~c = {3, −3, −2} ,

|~a − 2~c | = p

=

√

~ p

( ~a − 2~c, ~a − 2~c )

·

−

·

−

−

·

−

= 3

3 + (

3)

(

3) + (

2)

(

2) = 22,

звiдки

( 3~a + 2b, ~a − 2~c ) = −3 · 3 + (−1) · (−3) + 6 · (−2) = −18

~

Πp

( 3~a + 2~b ) =

( 3~a + 2b, ~a − 2~c )

=

−18

.

~a−2~c

|~a − 2~c |

√

д)

Обчислимо

22

~a − ~c = {2, −2, 0},

~

b − ~c = {−2, 0, −2},

= 2√

|~a − ~c | = p

= p

,

( ~a − ~c, ~a − ~c )

2 · 2 + (−2) · (−2) + 0 · 0

2

|~b − ~c | = q

=

p

(~b − ~c,~b − ~c )

√

= (−2) · (−2) + 0 · 0 + (−2) · (−2) = 2 2,

~

звiдки

( ~a − ~c, b − ~c ) = 2 · (−2) + (−2) · 0 + 0 · (−2) = −4,

~

π

( ~a

−

~c,

~b

−

~c ) = arccos

( ~a − ~c, b − ~c )

= arccos

−4

=

.

3

~

−

8

|~a − ~c || b − ~c |

28

e) Обчислимо
2~a + ~c = {1, −1, 6},			~
			2b − ~c = {−5, 1, −2},
p				p
	=
| 2~a + ~c | =	( 2~a + ~c, 2~a + ~c ) = 1 · 1 + (−1) · (−1) + 6 · 6 =
			√
	| 2~b − ~c | = q		38,
							=
		( 2~b − ~c, 2~b − ~c )
p								√
= (−5) · (−5) + 1 · 1 + (−2) · (−2) = 30,

~

( 2~a + ~c, 2b − ~c ) = 1 · (−5) + (−1) · 1 + 6 · (−2) = −18,

звiдки

~

( 2~a + ~c, 2~b

−

~c ) = arccos

( 2~a + ~c, 2b − ~c )

=

~

−18

| 2~a + ~c || 2b − ~c |

= arccos

= π

arccos

9

.

√

38

√

−

285

30

~

Приклад 3.2. Заданi два неколiнеарних вектори ~a i b. Знайти вектор ~x,

який задовольняє такi умови:

~

а) вектори ~a, b, ~x компланарнi;

б) ( a, x ) = 1, ( b, x ) = 0.

Розв’язання. Оскiльки

вектори

~

компланарнi,

то можна

~a, b, ~x

~

можна роз-

вважати, що вони лежать на однiй площинi. Вектори ~a, b

глядати як базис на цiй площинi, оскiльки вони неколiнеарнi. Нехай

	~			~
~x = {α, β} в базисi ~a, b, тобто ~x = α~a + βb. З другої умови випливає,
що		~		~
( ~a, ~x ) = ( ~a, α~a + βb ) = α( ~a, ~a ) + β( ~a, b ) = 1,
~	~	~	~	~ ~

( b, ~x ) = ( b, α~a + βb ) = α( b, ~a ) + β( b, b ) = 0.

29

З цих двох рiвнянь знайдемо α i β. Зауважимо, що ця система має

~ ~

~

2

> 0 (нерiвнiсть Кошi-

єдиний розв’язок, оскiльки ( ~a, ~a )( b, b ) − ( ~a, b )

Буняковського)1. Таким чином,

~ ~

~

α =

( b, b )

, β = −

( ~a, b )

~ ~

~

2

~ ~

~

2

( ~a, ~a )( b, b ) − ( ~a, b )

( ~a, ~a )( b, b ) − ( ~a, b )

i

~ ~

~

~

~x =

~a( b, b ) − b( ~a, b )

.

~ ~

~

2

( ~a, ~a )( b, b ) − ( ~a, b )

Приклад 3.3. Довжини базисних векторiв загальної декартової системи

√

координат у просторi дорiвнюють вiдповiдно 3, 2 i 1, кути мiж базисними векторами дорiвнюють ( ~e1, ~e2 ) = ( ~e1, ~e3 ) = π/6, ( ~e2, ~e3 ) = π/4.

~

Обчислити довжини векторiв ~a, b i кут мiж ними, якi в заданому базисi мають координати {2, 1, −1} та {−3, −1, 1} вiдповiдно.

~				i
Розв’язання. Вектори ~a i b заданi своїми координатами в базисi ~e1, ~e2
~e3, тому	~
~a = −2~e1 + ~e2 − ~e3,		+ ~e2	+ ~e3.
	b = −3~e1

Перш нiж знаходити довжини сторiн i кути трикутника, обчислимо всi можливi скалярнi добутки базисних векторiв:

( ~e1, ~e1 ) = |~e1 |2 = 3, ( ~e2, ~e2 ) = |~e2 |2 = 4,	( ~e3, ~e3 ) = |~e3 |2 = 1,
( ~e1, ~e2 ) = |~e1 ||~e2 | cos ( ~e1, ~e2 ) =		3,
	√
( ~e2, ~e3 ) = |~e2 ||~e3 | cos ( ~e2, ~e3 ) =		2,
( ~e1, ~e3 ) = |~e1 ||~e3 | cos ( ~e1, ~e3 ) =		3		.
		2

Квадрат довжини вектора ~a дорiвнює:

|~a |2 = ( ~a, ~a ) = ( −2~e1 + ~e2 − ~e3, −2~e1 + ~e2 − ~e3 ) = 4( ~e1, ~e1 )+

√

+( ~e2, ~e2 ) + ( ~e3, ~e3 ) − 4( ~e1, ~e2 ) + 4( ~e1, ~e3 ) − 2( ~e2, ~e3 ) = 11 − 2 2,

1 ( )(~ ~

У загальному випадку нерiвнiсть Кошi-Буняковського має такий вигляд ~a, ~a b, b

0 причому знак рiвностi має мiсце тодi i лише тодi, коли вектори i ~ колiнеарнi.

, ~a b

) − ( ~ )2 ≥

~a, b

30