
- •§1. Основные понятия
- •§2. Признаки сходимости знакопостоянных рядов
- •I. Необходимый признак сходимости рядов
- •II. Признак Даламбера
- •III. Радикальный признак Коши
- •IV. Интегральный признак Коши
- •V. Признаки сравнения
- •§3. Признаки сходимости знакопеременных рядов
- •§4. Степенные ряды
- •§5. Ряды Маклорена и Тейлора
- •§6. Применение рядов в приближенных вычислениях
- •§1. Основные понятия 3
IV. Интегральный признак Коши
Теорема.Пусть члены ряда![]() положительны и пусть
положительны и пусть![]() такая непрерывная функция, что
такая непрерывная функция, что![]() ,
,![]() ,
…
,
…![]() ,
…, причем функция
,
…, причем функция![]() невозрастающая на интервале
невозрастающая на интервале![]() при некотором
при некотором![]() .
Тогда справедливы следующие утверждения:
.
Тогда справедливы следующие утверждения:
1) если несобственный интеграл
![]() сходится, то сходится и ряд
сходится, то сходится и ряд![]() ,
,
2) если несобственный интеграл
![]() расходится, то расходится и ряд
расходится, то расходится и ряд![]() .
.
Для краткости говорят: «Ряд и интеграл ведут себя одинаково».
Замечание.Для применения интегрального признака
к исследованию сходимости ряда![]() надо подобрать такую функцию
надо подобрать такую функцию![]() ,
что
,
что![]() ,
т.е. попросту говоря, выписать
,
т.е. попросту говоря, выписать![]() и заменить в немn
на x, и затем
исследовать сходимость интеграла
и заменить в немn
на x, и затем
исследовать сходимость интеграла![]() .
Это имеет смысл делать только тогда,
когда полученный интеграл достаточно
легко вычисляется.
.
Это имеет смысл делать только тогда,
когда полученный интеграл достаточно
легко вычисляется.
Примеры
1) Применим интегральный признак к
исследованию на сходимость ряда вида
![]() ,
,![]() ,
называемогообобщенным гармоническим
рядом или рядом Дирихле.
,
называемогообобщенным гармоническим
рядом или рядом Дирихле.
Решение.В этом случае
требуемой функцией является![]() .
Функция
.
Функция![]() является невозрастающей на интервале
является невозрастающей на интервале![]() .
Вычислим
.
Вычислим![]() .
.
Если
![]() ,
то
,
то![]() .
.
Если
![]() ,
то
,
то .
.
Следовательно, несобственный интеграл
сходится при
![]() и расходится при
и расходится при![]() .
То же самое можно сказать и о данном
ряде.
.
То же самое можно сказать и о данном
ряде.
Запомнить!Обобщенный гармонический
ряд![]() сходится при
сходится при![]() и расходится при
и расходится при![]() .
.
2) Исследовать на сходимость ряд
![]() .
.
Решение.Выписав![]() и заменив в немn на
x, получим функцию
и заменив в немn на
x, получим функцию![]() .
.
Внимание!Пока мы не убедились,
что функция невозрастающая на некотором
интервале вида![]() ,
к интегрированию переходить рано!
,
к интегрированию переходить рано!
Исследуем функцию
![]() на монотонность с помощью производной:
на монотонность с помощью производной: .
Критическая точка
.
Критическая точка![]() ,
на интервале
,
на интервале![]()
![]() ,
т.е. функция
,
т.е. функция![]() невозрастающая. Теперь можно переходить
к интегрированию.
невозрастающая. Теперь можно переходить
к интегрированию.
![]() ,
,![]() интеграл расходится, расходится и данный
ряд.
интеграл расходится, расходится и данный
ряд.
V. Признаки сравнения
Теорема.Первый признак сравнения(признак сравнения в форме неравенства). Пусть даны два ряда с положительными членами:
![]() (2.5)
(2.5)
![]() (2.6)
(2.6)
причем
члены первого ряда не превосходят членов
второго при любом
![]() ,
т.е.
,
т.е.
![]() (2.7)
(2.7)
Тогда: а) если сходится ряд (2.6), то сходится и ряд (2.5)
б) если расходится ряд (2.5), то расходится и ряд (2.6).
Удобно применять другую формулировку этой теоремы:
а) если больший ряд сходится, то меньший ряд тоже сходится;
б) если меньший ряд расходится, то больший ряд тоже расходится.
Примеры
Исследовать сходимость следующих рядов:
1)
![]()
Решение.Сравним данный ряд с
гармоническим![]() ,
мысленно отбросив его первый член,
равный 1 (что, естественно, не повлияет
на сходимость ряда). Т.к.
,
мысленно отбросив его первый член,
равный 1 (что, естественно, не повлияет
на сходимость ряда). Т.к.![]() ,
,![]() ,
и вообще,
,
и вообще,![]() (ведь
(ведь![]() ),
то члены данного ряда больше членов
расходящегося гармонического ряда, и,
следовательно, на основании признака
сравнения данный ряд расходится.
),
то члены данного ряда больше членов
расходящегося гармонического ряда, и,
следовательно, на основании признака
сравнения данный ряд расходится.
Понятно, что для применения признака сравнения в форме неравенства нужно сначала установить подходящее неравенство. При этом часто пользуются следующими стандартными неравенствами:
![]() ,
(2.8)
,
(2.8)
![]() ,
,
![]() .
.
Иногда приходится применять более сложные неравенства:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() при некотором
при некотором![]() .
.
2)
![]()
Решение.Прежде всего,
заметим, что это ряд с положительными
членами, т.к. синус возводится в четную
степень. Далее очевидное неравенство![]() позволяет заключить, что
позволяет заключить, что![]() ,
а поскольку ряд
,
а поскольку ряд![]() сходится, то и ряд с меньшими членами
сходится, то и ряд с меньшими членами![]() тоже сходится.
тоже сходится.
3)
![]()
Решение.Преобразуем выражение, стоящее под знаком суммы, следующим образом:
![]()
![]()
(здесь
мы учли, что
![]() ).
).
Т.к. ряд
![]() – сходится (как обобщенный гармонический
при
– сходится (как обобщенный гармонический
при![]() ),
то исследуемый ряд также сходится.
),
то исследуемый ряд также сходится.
Отметим «эталонные» ряды, часто используемые для сравнения:
а) геометрический ряд![]() – сходится при
– сходится при![]() ,
расходится при
,
расходится при![]() ,
,
б) обобщенный гармонический ряд![]() сходится при
сходится при![]() и расходится при
и расходится при![]() .
.
Нестандартность применения признака сравнения заключается в том, что надо не только подобрать соответствующий «эталонный» ряд, но и доказать неравенство (2.7), для чего часто требуется преобразование рядов (например, отбрасывание или приписывание конечного числа членов, умножение на определенные числа и т. п.). Более простым оказывается признак сравнения в предельной форме – ведь вычислять пределы обычно гораздо проще, чем доказывать неравенства.
Теорема.Второй признак
сравнения(признак сравнения в
предельной форме). Если![]() и
и![]() – ряды с положительными членами и
существует предел отношения их общих
членов
– ряды с положительными членами и
существует предел отношения их общих
членов![]() ,
причем
,
причем![]() ,
то ряды ведут себя одинаково: либо
одновременно сходятся, либо одновременно
расходятся.
,
то ряды ведут себя одинаково: либо
одновременно сходятся, либо одновременно
расходятся.
Чаще всего исследуемый ряд сравнивают
с обобщенным гармоническим рядом
![]() ,
причемpудобно
подбирать в процессе сравнения, как это
сделано ниже в примере 1.
,
причемpудобно
подбирать в процессе сравнения, как это
сделано ниже в примере 1.
Примеры
1)
![]()
Решение. Сравним данный ряд с
обобщенным гармоническим рядом![]() ,
причемpподберем в
процессе сравнения.
,
причемpподберем в
процессе сравнения.
Выпишем предел
![]() и преобразуем его:
и преобразуем его:
 (2.9)
(2.9)
Мы пришли к пределу отношения двух
степенных выражений на бесконечности.
Если степень числителя меньше степени
знаменателя, то предел равен 0, а это тот
случай, когда признак сравнения в
предельной форме не работает. Если
степень числителя больше степени
знаменателя, то предел равен
![]() ,
а это опять тот случай, когда признак
сравнения в предельной форме не работает.
Таким образом, нас устроит только случай,
когда степень числителя равна степени
знаменателя, т.е.
,
а это опять тот случай, когда признак
сравнения в предельной форме не работает.
Таким образом, нас устроит только случай,
когда степень числителя равна степени
знаменателя, т.е.![]() ,
или
,
или![]() (в этом случае предел равен отношению
старших коэффициентов, т.е. не 0 и не
(в этом случае предел равен отношению
старших коэффициентов, т.е. не 0 и не![]() ).
Итак, исследуемый ряд ведет себя так
же, как и ряд
).
Итак, исследуемый ряд ведет себя так
же, как и ряд![]() ,
т.е. сходится.
,
т.е. сходится.
Разумеется, решение похожих задач не
надо расписывать так подробно. Обычно,
выписав предел (2.9), далее пишут
![]()
![]()
![]()
![]() сходится.
Ясно, что слово «сходится» относится
сразу к двум рядам и к
сходится.
Ясно, что слово «сходится» относится
сразу к двум рядам и к![]() ,
и к исходному ряду.
,
и к исходному ряду.
Следствием второго (предельного) признака сравнения является третий признак сравнения.
Теорема.Третий признак сравнения(признак сравнения в форме эквивалентных б.м. или кратко эквивалентный признак сравнения). В общем члене ряда бесконечно малый множитель или делитель можно заменить на эквивалентный, поведение ряда (сходимость или расходимость) от этого не изменится.
Замечание 1.Напомним таблицу
эквивалентных бесконечно малых величин
(при![]() ):
):
![]() .
.
Замечание 2.При работе с
эквивалентным признаком сравнения
необходимо помнить, что таблица
эквивалентных бесконечно малых величин
выписана при![]() ,
а в рядах всегда
,
а в рядах всегда![]() ,
т.е.nявляется бесконечно
большой. А вот бесконечно малыми являются
величины вида:
,
т.е.nявляется бесконечно
большой. А вот бесконечно малыми являются
величины вида:![]() (и вообще
(и вообще![]() при
при![]() ),
),![]() (и вообще
(и вообще![]() при
при![]() ).
).
2)
![]()
Решение.Т.к. при![]()
![]() (т.е.
(т.е.![]() – б.м.), то
– б.м.), то![]() ,
и ряд
,
и ряд![]() ведет себя так же, как и ряд
ведет себя так же, как и ряд![]() – обобщенный гармонический ряд приp=1/2<1, т.е. расходится.
– обобщенный гармонический ряд приp=1/2<1, т.е. расходится.
На практике запись ведут кратко:
![]()
![]() – расходится. Ясно, что слово «расходится»
относится к обоим рядам.
– расходится. Ясно, что слово «расходится»
относится к обоим рядам.
3)
![]() .
.
Решение.Т.к.![]() ,то
,то![]() ,
ряд
,
ряд![]() знакоположительный, и к нему можно
применять эквивалентный признак
сравнения. Поскольку
знакоположительный, и к нему можно
применять эквивалентный признак
сравнения. Поскольку![]() – б.м. при
– б.м. при![]() ,
то
,
то![]()
![]()
![]() и
и![]()
![]()
![]() =
=![]() .
.
Последний ряд легко исследуется по признаку Даламбера (он сходится).
Несмотря на то, что предельный и эквивалентный признаки сравнения более просты по сравнению с признаком сравнения в форме неравенства, иногда без первого признака не обойтись. Покажем это на следующем примере, а заодно продемонстрируем, как надо рассуждать в общем и целом при исследовании рядов на сходимость.
4)
![]()
Решение.Проверим необходимый
признак:![]() – необходимый признак не работает.
Попробуем применить признак Даламбера:
– необходимый признак не работает.
Попробуем применить признак Даламбера:
![]() ,
,
т.е. вопрос о сходимости ряда остается открытым. Этого следовало ожидать (см. замечаниек признаку Даламбера).
Применим признак сравнения в предельной форме. Сравним данный ряд, например, с гармоническим рядом:
![]() ,
,
т.е. ответа о сходимости ряда нет. Аналогичная картина наблюдается и при использовании других «эталонных» рядов.
Применим, наконец, признак сравнения в
форме неравенства (первый признак
сравнения). Сравним данный ряд с
гармоническим, у которого отброшен
первый член:
![]() ...
Т.к. члены рассматриваемого ряда больше
членов расходящегося гармонического
...
Т.к. члены рассматриваемого ряда больше
членов расходящегося гармонического![]() ,
что вытекает из неравенства (2.8), то
данный ряд расходится.
,
что вытекает из неравенства (2.8), то
данный ряд расходится.
Отметим, что для исследования сходимости
данного ряда неприменим и интегральный
признак, т.к. первообразная подынтегральной
функции не является элементарной
функцией, т.е. соответствующий
неопределенный интеграл
![]() является «не берущимся».
является «не берущимся».
Задачи
А)Исследовать ряды с помощью признака Даламбера:
1.
![]() 2.
2.![]() 3.
3.![]()
4.
![]() 5.
5.![]() 6.
6.![]()
B)Исследовать ряды с помощью радикального признака Коши:
7.
![]() 8.
8.![]() 9.
9.![]() 10.
10.![]()
C)Исследовать ряды с помощью интегрального признака Коши:
11.
![]() 12.
12.![]() 13.
13.![]()
14.
![]() 15.
15.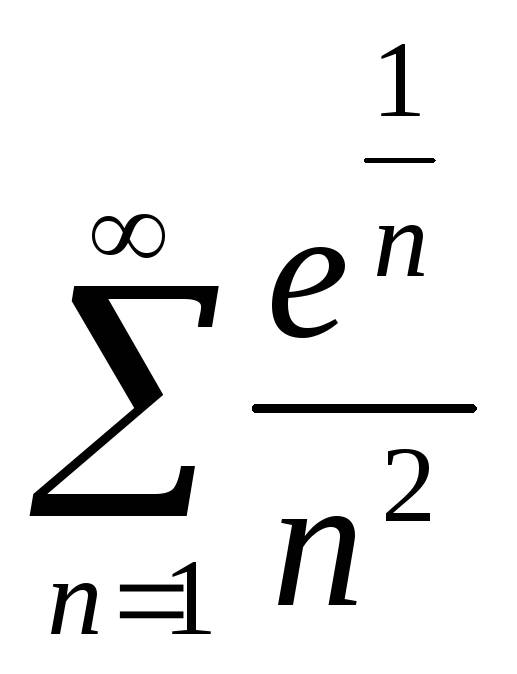
D)Исследовать ряды с помощью признаков сравнения:
16.
![]() 17.
17.![]() 18.
18.![]()
19.
![]() 20.
20.![]() 21.
21.![]()
Е)Исследовать ряды на сходимость:
22.
![]() 23.
23.![]() 24.
24.![]()
25.
![]() 26.
26.![]() 27.
27.![]()
28.
![]() 29.
29.![]() 30.
30.![]()
31.
![]() 32.
32.![]() 33.
33.![]()
34.
![]() 35.
35.![]() 36.
36.![]()
37 .
![]() 38.
38.![]() 39.
39.![]()
40.
![]() 41.
41.![]() 42.
42.![]()
43.
![]() 44.
44.![]() .
.
