§5. Степенные ряды

До сих пор рассматривали ряды, членами которых были числа, т.е. числовые ряды. Теперь перейдем к рассмотрению рядов, членами которых являются функции, в частности, степенные функции с целыми неотрицательными показателями степени:

(1)

Определение. Такой ряд называютсястепенным, а числаназываютсякоэффициентамистепенного ряда.

Рассматривают и степенные ряды более общего вида:

(2)

(по степеням ). Такой ряд не отличается существенно от ряда вида (1), ибо приводится к нему простой заменой переменной:.

Определение.Множество значений, при которых степенной ряд (1) или (2) сходится, называетсяобластью сходимостистепенного ряда.

Структура области сходимости степенного ряда устанавливается с помощью следующей теоремы:

Теорема Абеля.

1) Если степенной ряд вида (1), т.е. по степеням , сходится при значении(отличном от нуля), то он сходится, и притом абсолютно, при всех значенияхтаких, что.

2) Если степенной ряд вида (1) расходится при значении , то он расходится при всех значенияхтаких, что.

Из теоремы Абеля вытекает следующая теорема.

Теорема. Областью сходимости степенного ряда вида (2), т.е. ряда по степеням, является интервал с центром в точкеи с концами в точкахи.

Число получило названиерадиуса сходимости, а интервал–интервала сходимостистепенного ряда. На концах интервала сходимости, т.е. приивопрос о сходимости или расходимости данного ряда решается индивидуально для каждого конкретного ряда.

У некоторых рядов интервал сходимости вырождается в точку (при), у других охватывает всю числовую ось (при).

Для начала укажем способ определения интервала сходимости степенного ряда на примере ряда (1).

Рассмотрим ряд, составленный из абсолютных величин членов этого ряда:

(3)

Т.к. при каждом конкретном ряд (3) является числовым знакоположительным рядом, то для выяснения вопроса о его сходимости можно воспользоваться признаком Даламбера:

Допустим, что существует

.

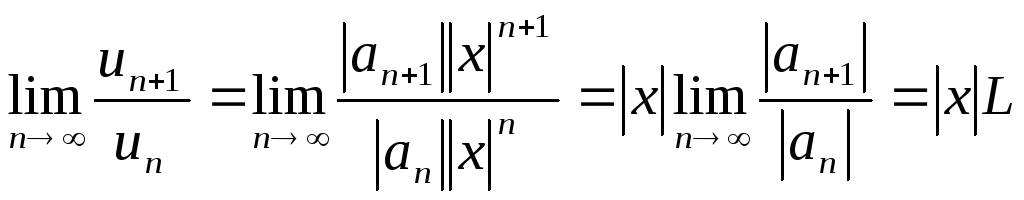Тогда, по признаку Даламбера ряд сходится, если (т.е. при), и расходится, если(т.е. при).

Следовательно, ряд (1) сходится абсолютно при и расходится при, и интервалом сходимости является интервал, а радиусом сходимости является число.

При признак Даламбера не дает ответа на вопрос о сходимости, поэтому необходимо, подставляя значенияв ряд (1), исследовать получающиеся числовые ряды в каждом конкретном случае.

Замечание: Интервал сходимости можно найти, используя радикальный признак Коши (также применяя его к ряду (3)):

.

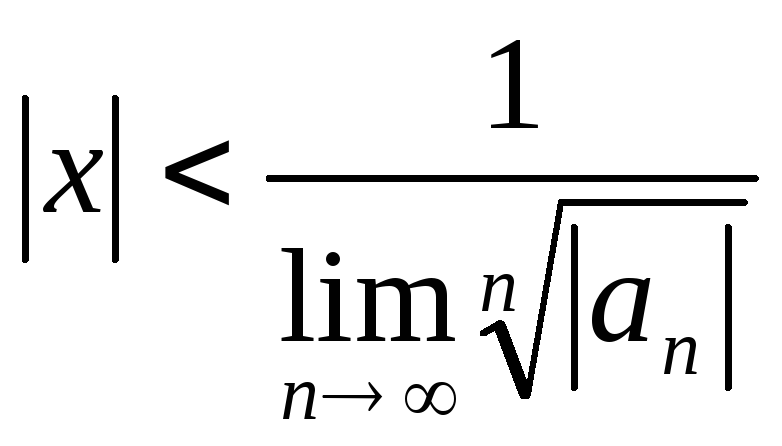Примеры.

Найти области сходимости степенных рядов:

1)

Решение.Рассмотрим ряд, составленный из абсолютных величин членов данного ряда

.

Применим к нему признак Даламбера.

Отсюда получаем интервал сходимости: .

Исследуем сходимость на концах интервала:

При исходный ряд принимает вид:– это обобщенный гармонический ряд при, а значит, он сходится. Приполучаем абсолютно сходящийся ряд, т.к. ряд, составленный из модулей его членов, сходится.

Следовательно, интервал сходимости ряда имеет вид: .

2) .

Решение. Ряд, составленный из модулей, имеет вид:

.

ряд сходится при любых. Таким образом, интервалом сходимости является интервал.

3)

Решение. Ряд, составленный из абсолютных величин членов данного ряда, исследуем с помощью радикального признака Коши: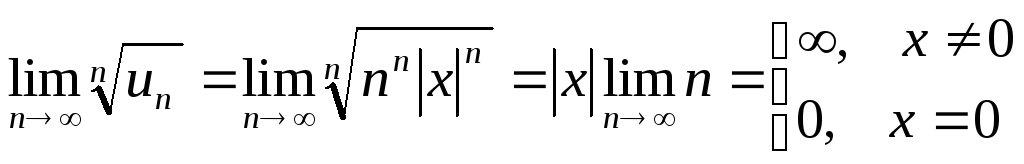

Следовательно, область сходимости ряда состоит из одной точки .

4)

Решение.

.

Отсюда получаем интервал сходимости: .

При исходный ряд имеет вид:– это расходящийся ряд (обобщенный гармонический при). Подставляя, получаем условно сходящийся ряд. Окончательно, интервал сходимости ряда имеет вид:.

Свойства степенных рядов:

1. Сумма степенного ряда является непрерывной функцией во всем интервале сходимости ряда.

2. Степенной ряд можно почленно интегрировать по любому отрезку , лежащему в интервале сходимости

.

3. Степенной ряд внутри интервала сходимости можно почленно дифференцировать сколь угодно раз. При этом будут получаться степенные ряды с тем же радиусом сходимости:

Задачи.

Найти области сходимости степенных рядов:

1 2.3.

4. 5.6.

7. 8.9.

10. 11.12.

13. 14.15.

16. 17.18.

19. 20.21.

22.23.24.

25. 26.(Указание: при исследовании сходимости на правом конце интервала учесть, что факториалы больших чисел могут быть выражены приближенно формулой Стирлинга).