
- •Введение в теорию рядов
- •§1. Основные понятия
- •§2. Свойства сходящихся рядов
- •§3. Признаки сходимости знакопостоянных рядов
- •I. Необходимый признак сходимости рядов.
- •II. Признак Даламбера.
- •III. Радикальный признак Коши.
- •IV. Интегральный признак Коши.
- •§4. Признаки сходимости знакопеременных рядов
- •§5. Степенные ряды
- •§6. Ряды Маклорена и Тейлора
- •§7. Разложение в ряд Маклорена некоторых функций
- •§8. Применение рядов в приближенных вычислениях
§6. Ряды Маклорена и Тейлора
Предположим, что функция
![]() ,
определенная и бесконечно дифференцируемая
в окрестности точки
,
определенная и бесконечно дифференцируемая
в окрестности точки![]() ,
может быть представлена в виде суммы
степенного ряда или, другими словами,
может быть разложена в степенной ряд
,
может быть представлена в виде суммы
степенного ряда или, другими словами,
может быть разложена в степенной ряд
![]()
Выразим коэффициенты ряда через
![]() .
Найдем производные функции
.
Найдем производные функции![]() ,
почленно дифференцируя ряд
,
почленно дифференцируя ряд![]() раз:
раз:
![]()
![]()
![]()
…………………………………………………………….
![]()
Полагая в полученных равенствах
![]() ,
получим
,
получим![]() ,
,![]() ,
,![]() ,
,![]() ,
…,
,
…,![]() ,
откуда
,
откуда
![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,…
,…
Подставляя значения коэффициентов
![]() ,
получим ряд:
,
получим ряд:
![]() (1)
(1)
называемый рядом Маклорена.
Отметим, что не все функции могут быть
разложены в ряд Маклорена. Может
оказаться, что ряд Маклорена, составленный
формально для функции
![]() ,
является расходящимся или сходящимся
не к функции
,
является расходящимся или сходящимся
не к функции![]() .
.
Если представить ряд Маклорена в виде
![]() ,
где
,
где![]() –
–
![]() -я
частичная сумма ряда,
-я
частичная сумма ряда,![]() –
–![]() -й
остатокряда, то можно сформулировать
следующую теорему:
-й
остатокряда, то можно сформулировать
следующую теорему:
Теорема. Для того чтобы ряд Маклорена
сходился к функции![]() ,
необходимо и достаточно, чтобы при
,
необходимо и достаточно, чтобы при![]() остаток ряда стремился к нулю, т.е.
остаток ряда стремился к нулю, т.е.![]() для всех значений
для всех значений![]() из интервала сходимости ряда.
из интервала сходимости ряда.
Можно доказать, что если функция
![]() разложима в ряд Маклорена, то это
разложение единственное.
разложима в ряд Маклорена, то это
разложение единственное.
Замечание. Ряд Маклорена является частным случаемряда Тейлора:
![]() при
при![]()
Ряд Тейлора тесно связан с формулой Тейлора:
![]() ,
где
,
где![]() – остаточный член формулы Тейлора,
который можно записатьв форме Лагранжа:
– остаточный член формулы Тейлора,
который можно записатьв форме Лагранжа:
![]() ,
,![]() .
.
§7. Разложение в ряд Маклорена некоторых функций
1.
![]()
Имеем
![]() ;
;
![]() ,
и по формуле (1) получаем
,
и по формуле (1) получаем
![]() . (2)
. (2)
Областью сходимости этого степенного
ряда является интервал
![]() .
.
2.
![]()
Имеем:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
откуда
,
откуда
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() и т.д.
и т.д.
Очевидно, что производные четного
порядка
![]() ,
а нечетного порядка
,
а нечетного порядка![]() ,
,![]() ,
и по формуле (1)
,
и по формуле (1)
(?)![]() (3)
(3)
Область сходимости ряда
![]() .
.
3.
![]() .
.
Рассматривая аналогично функции
![]() ,
получим:
,
получим:
![]() (4)
(4)
Область сходимости ряда
![]() .
.
4.
![]() ,
где
,
где![]() – любое действительное число.
– любое действительное число.
Имеем
![]() ,
,![]() ,
,
![]() ,
,![]() ,
…,
,
…,
![]() ,
…
,
…
При
![]() :
:![]() ,
,![]() ,
,![]() ,
,
![]() ,
…,
,
…,![]() и по формуле (1) получаем
и по формуле (1) получаем
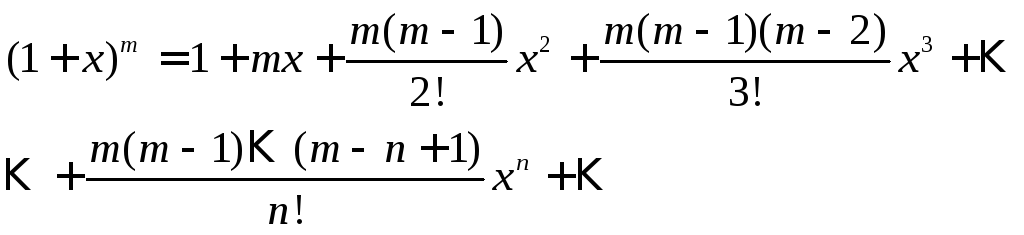 (5)
(5)
Найдем интервал сходимости ряда:
Ряд, составленный из модулей
![]() ,
исследуем с помощью признака Даламбера:
,
исследуем с помощью признака Даламбера:
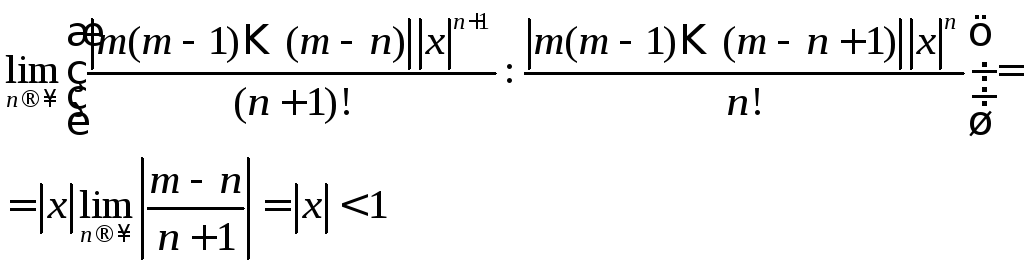 .
.
Следовательно, интервал сходимости
ряда
![]() .
На концах интервала при
.
На концах интервала при![]() сходимость ряда зависит от конкретных
значений
сходимость ряда зависит от конкретных
значений![]() .
.
Ряд (5) называется биномиальным. Если![]() – целое положительное число, то
биномиальный ряд представляет формулубинома Ньютона, так как при
– целое положительное число, то
биномиальный ряд представляет формулубинома Ньютона, так как при![]() сомножитель
сомножитель![]() равен нулю, следовательно,
равен нулю, следовательно,![]() -й
член ряда и все последующие равны
нулю, т.е. ряд обрывается, и вместо
бесконечного разложения получается
конечная сумма.
-й
член ряда и все последующие равны
нулю, т.е. ряд обрывается, и вместо
бесконечного разложения получается
конечная сумма.
Выпишем некоторые разложения функции
![]() при различных
при различных![]() .
.
![]() :
:
![]() ,
,![]() (6)
(6)
если в это разложение подставить
![]() вместо
вместо![]() ,
получим:
,
получим:
![]() (7)
(7)
![]() :
:
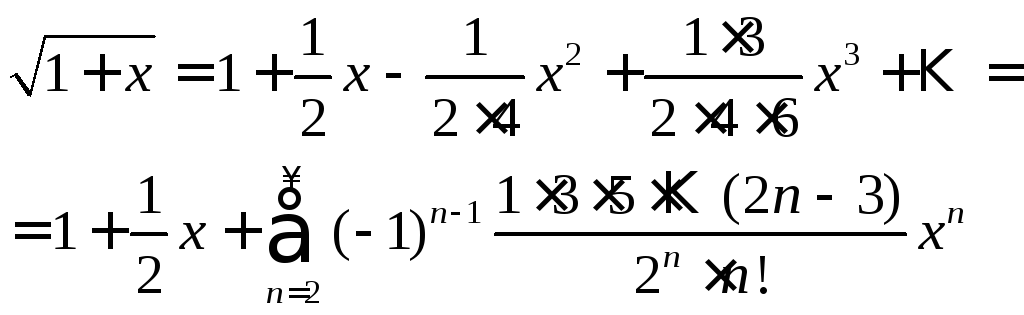 ,
,![]() (8)
(8)
![]() :
:
 ,
,![]() (9)
(9)
5.
![]() .
.
Получить разложение для этой функции,
непосредственно вычисляя коэффициенты
с помощью производных, не очень просто,
поэтому мы воспользуемся разложением
(6) и свойством 2) степенных рядов.
Интегрируя почленно равенство (6) в
интервале
![]() ,
где
,
где![]() ,
с учетом того, что
,
с учетом того, что![]() ,
получим
,
получим
![]() (10)
(10)
Область сходимости ряда (после выяснения
сходимости на концах интервала) есть
![]() .
.
6.
![]()
Проделаем то же самое, что и в предыдущем случае, воспользовавшись разложением (7):
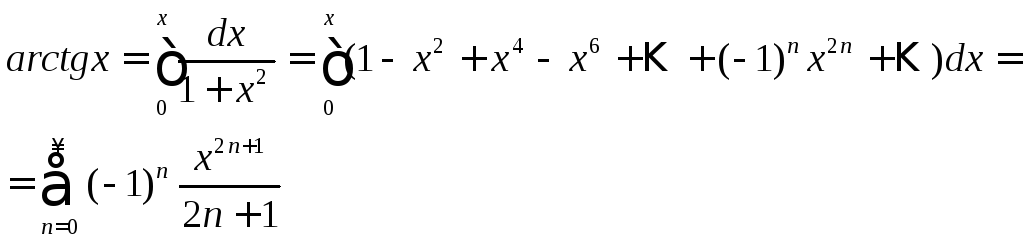 (11)
(11)
Область сходимости ряда
![]() .
.
7.
![]()
Воспользуемся разложением (9), подставив
в него
![]() вместо
вместо![]() :
:
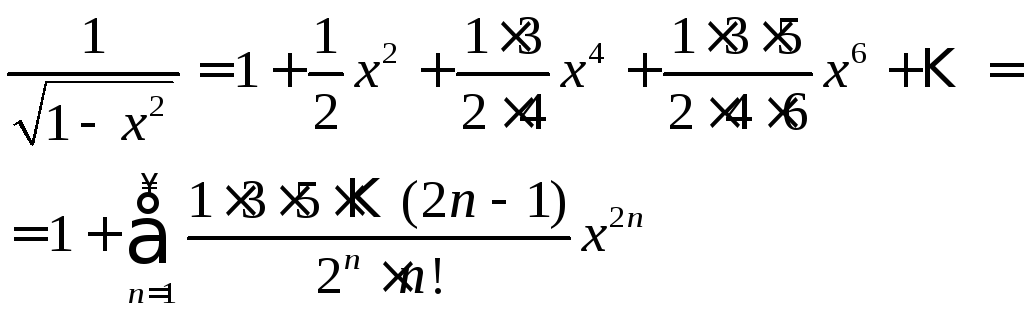
Интегрируя в интервале
![]() ,
где
,
где![]() ,
получаем:
,
получаем:
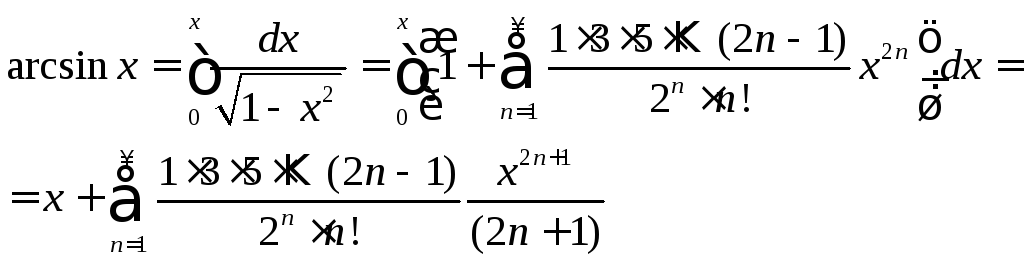 (12)
(12)
Область сходимости ряда
![]()
Можно доказать, что ряды, приведенные в формулах (2) –(12), сходятся к функциям, для которых они составлены.
При разложении более сложных функций часто используют готовые разложения (2) – (12).
Примеры.
1) Разложить в ряд Маклорена функцию
![]()
Решение. Воспользуемся известной
тригонометрической формулой![]()
Разложим в ряд Маклорена функцию
![]() ,
заменяя в разложении (4)
,
заменяя в разложении (4)![]() на
на![]() :
:

Тогда
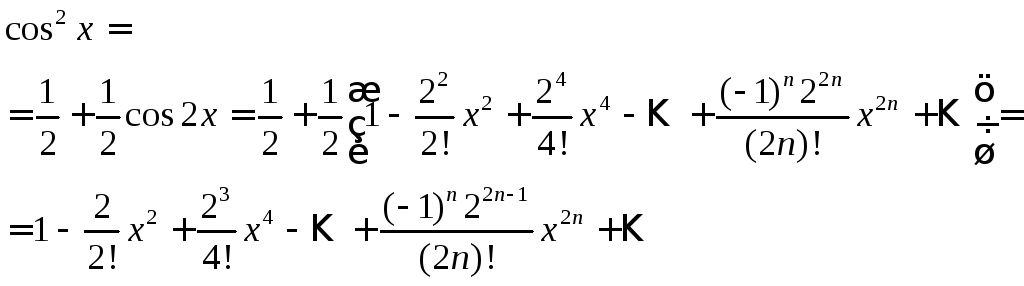
Это и есть разложение в ряд Маклорена
функции
![]() .
Очевидно, что оно справедливо при любом
.
Очевидно, что оно справедливо при любом![]() .
.
2) Разложить в ряд Тейлора по степеням
![]() функцию
функцию![]()
Решение.Преобразуем данную функцию так, чтобы можно было воспользоваться разложением (6):
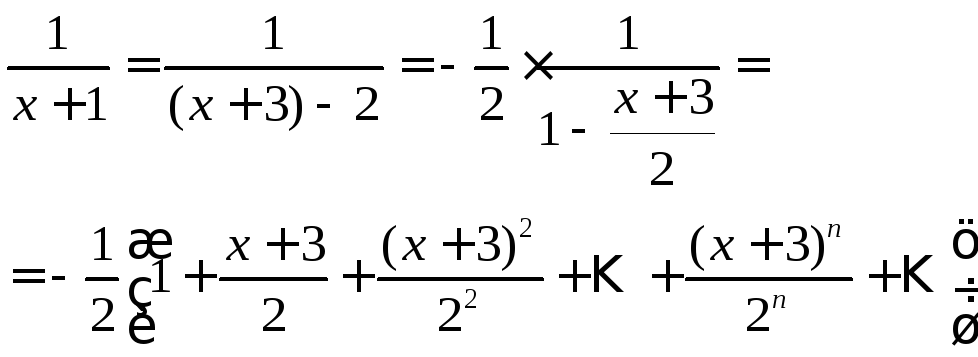
Полученное разложение справедливо,
когда
![]() .
Отсюда получаем
.
Отсюда получаем![]() или
или![]() .
.
