Лекция № 6. Математическая индукция

1. Сумма нечетных чисел

Математическая индукция играет огромную роль в дискретной математике (именно в силу ее дискретного характера). Полученные этим методом доказательства в данной области математики почти столь же надежны, как и те, что выведены дедуктивным путем. Начнем с вопроса: «Что мы получим, если просуммируем первые n нечетных чисел?». Непосредственные вычисления дают следующий результат.

1 = 1

1+3 = 4

1+3+5 = 9

1+3+5+7 = 16

1+3+5+7+9 = 25

1+3+5+7+9+11 = 36

1+3+5+7+9+11+13 = 49

1+3+5+7+9+11+13+15 = 64

1+3+5+7+9+11+13+15+17 = 81

1+3+5+7+9+11+13+15+17+19 = 100

Можно заметить, что в каждом случае сумма равна . Так ли будет для всех остальных случаев при любом n? Для доказательства этого необходимо применить метод математической индукции, который заключается в следующем.

Допустим, что мы хотим доказать какое-либо свойство для любых положительных целых чисел: . Также предположим, что мы можем доказать два факта:

(а) единица имеет это свойство, и

(б) если n – 1 имеет это свойство, то n также обладает этим свойством. Принцип математической индукции утверждает, что если верны пункты (а) и (б), то каждое натуральное число обладает данным свойством.

Применим этот принцип к рассмотренному выше примеру суммы первых n нечетных чисел. Мы подозреваем, что эта сумма равна для любого n. То есть:

1+3+…+ (2n–3) + (2n–1) =.

Единица обладает этим свойством: . Допустим, что n–1 также обладает этим свойством. Тогда можем записать:

.

Добавляя к этой сумме член (2n–1), получим:

,

что и следовало доказать.

2. Сумма натуральных чисел

А теперь используем метод индукции для доказательства того, что сумма первых n положительных целых чисел равна . Если n = 1, то , т.е. единица обладает указанным свойством. Предположим, что сумма первых n – 1 натуральных чисел также обладает этим свойством, т.е. она равна: . Прибавив к этой сумме число n, получим:

.

Таким образом, сумма первых n положительных целых чисел также обладает указанным свойством. Значит, мы можем утверждать, что данная формула справедлива для любого натурального n.

Необходимо заметить, что метод индукции позволяет проверять уже известные формулы, но не позволяет выводить новые формулы. Для получения новых формул приходится напрягать творческие способности. Приведем следующий исторический пример.

Карл Фредерик Гаусс (1777-1855), один из наиболее великих математиков всех времен и народов, учился в начальной школе, когда его учитель задал классу задачу просуммировать все целые числа от 1 до 1000, он рассчитывал на час отдыха, пока его ученики будут заняты делом. Каково же было его удивление, когда Гаусс почти мгновенно получил правильный ответ! Его решение было предельно простым: суммируя первое число с последним, он получил 1 + 1000 = 1001; суммируя второе с предпоследним: 2 + 999 = 1001 и т.д. Всего сумм, равных 1001, получилось пятьсот. Таким образом, ответ равен: 500 · 1001 = 1000 · 1001/2 = 500500.

3. Снова считаем подмножества

Доказывая теорему 5.1. мы неявно пользовались методом математической индукции. Теперь пришло время применить его явно. Итак, мы подозреваем, что число всех подмножеств множества из n элементов равно . Если n = 1, то . То есть мы имеем пустое подмножество и подмножество, состоящее только из одного элемента – результат получился верный. Допустим, что множество состоит из n – 1 элементов, тогда общее количество подмножеств равно . Полагаем это утверждение истинным.

Добавление еще одного элемента в исходное множество приведет к тому, что появятся новые подмножества. Всего таких новых подмножеств будет , поскольку мы можем добавить новый элемент в каждое «старое» подмножество (в том числе, и в пустое множество). В результате получим, что общее количество подмножеств дополненного множества равно:

.

Таким образом, наш результат подтверждает теорему 5.1.

4. Биномиальные коэффициенты

Слово бином означает выражение, состоящее из двух членов, например: x + y. Бином является частным случаем полинома. Биномом Ньютона называется бином, возведенный в целую положительную степень: . Достаточно легко получить следующие частные формулы:

,

,

.

В общем случае формула разложения для бинома записывается так:

.

Или в сжатом виде

. (6.1)

Символы , где – обозначают целые положительные числа, называемые биномиальными коэффициентами. Здесь n – степень полинома, k – номер биномиального коэффициента.

Теорема 6.1. (Биномиальная теорема) Биномиальные коэффициенты рассчитываются по формуле:

, (6.2)

, .

Доказательство. Используем метод математической индукции. Если n=1, то , а . Это приводит к верному выражению: . Таким образом, для единицы данное свойство выполняется. Предположим, что оно также выполняется и для степениn – 1. Тогда, подставляя n – 1 вместо n в формулу (6.1) , получим:

.

Умножая это выражение на (x + y), приходим к выражению:

.

В последней сумме введем новую переменную . Если , то , а если , то . С учетом этого можем записать

.

Мы видим, что переменная суммирования в первой сумме изменяется от 0 до n – 1, а во второй сумме – от 1 до n. Чтобы уравнять пределы изменений этих переменных, вынесем первый член первой суммы и последний член второй суммы за знаки суммирования

.

Полученное уравнение можно записать следующим образом:

. (6.3)

С учетом формулы (6.2) выражение в квадратных скобках:

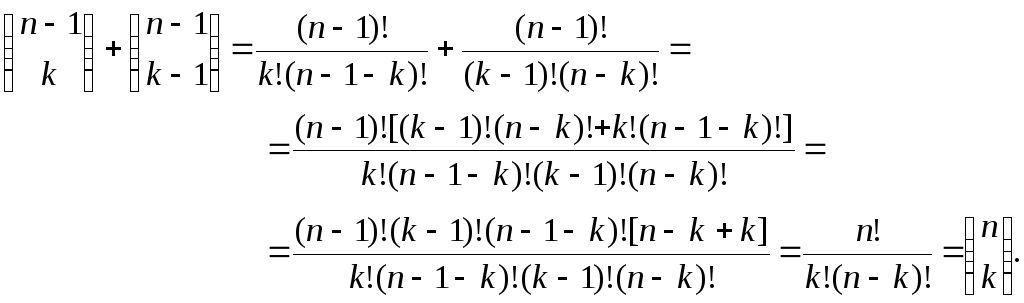
Подставляя полученный результат в уравнение (6.3), приходим к выражению (6.1). Таким образом, теорема доказана.

5. Треугольник Паскаля

Французский математик Блез Паскаль (1623-1662) составил таблицу из биномиальных коэффициентов. Она получилась треугольной, поскольку с увеличением степени бинома количество коэффициентов также увеличивается. Поэтому эту таблицу называют треугольником Паскаля. На рис. 6.1 показан треугольник Паскаля, в котором использованы формальные обозначения биномиальных коэффициентов.

Рис. 6.1. Треугольник Паскаля

На рис. 6.2 приведен треугольник Паскаля с числовыми значениями биномиальных коэффициентов. Эти значения могут быть получены с помощью формулы (6.2). Однако треугольник Паскаля дает возможность рассчитывать биномиальные коэффициенты без применения данной формулы. Если известны коэффициенты в какой-либо строке таблицы, то можно легко вычислить коэффициенты в соседней строке, которая находится ниже первой. Для определения каждого коэффициента нижней строки нужно сложить два коэффициента верхней строки, которые находятся слева и справа непосредственно над рассчитываемым коэффициентом. Таким образом, двигаясь от вершины треугольника вниз, можно последовательно рассчитать биномиальные коэффициенты для любой конечной степени бинома Ньютона. Это свойство следует из формулы, которую мы получили при доказательстве биномиальной теоремы

(6.4)

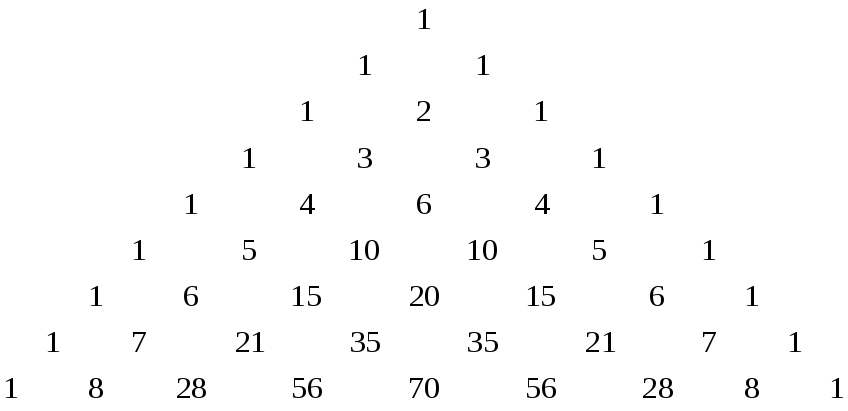
Рис. 6.2. Треугольник Паскаля с числовыми значениями коэффициентов

6. Бином Ньютона для дробных и отрицательных показателей

Формула бинома Ньютона (6.1) для целых положительных показателей была известна задолго до Исаака Ньютона (1643-1727), но им в 1676 году была указана возможность распространения этого разложения и на случай дробного или отрицательного показателя (хотя строгое обоснование этого было дано лишь норвежским математиком Нильсом Хенриком Абелем (1802-1829) в 1826 году).

В этом, более общем, случае формула бинома Ньютона начинается так же, как и формула (4.1), биномиальным коэффициентом служит выражение:

,

которое в случае целого положительного n, обращается в нуль при всяком , вследствие чего формула (6.1) содержит лишь конечное число членов. В случае же дробного (или отрицательного) n все биномиальные коэффициенты отличны от нуля, и правая часть формулы содержит бесконечный ряд членов (биномиальный ряд). Если , то этот ряд сходится, т.е., взяв достаточно большое число его членов, можно получить величину, сколь угодно близкую к .

7. Гамма-функция

Биномиальная теорема определяет биномиальные коэффициенты через факториалы чисел n и k:

.

По сути, факториал является функцией аргумента n. Однако это дискретная (решетчатая) функция, определенная только при целых значениях аргумента n = 1, 2, … Поэтому формула (6.2) пригодна только для целых n.

Возникает вопрос: существует ли непрерывная функция непрерывного аргумента , которая в частных случаях целого аргумента  = n равнялась бы ? На этот вопрос следует дать положительный ответ. Такая функция существует и называется она гамма-функцией (Г-функцией). Эта функция обладает свойством: .Ее график приведен на рис. 6.3.

Гамма-функция определяется с помощью интеграла Эйлера:

,

где  > 0.

При   0 интеграл расходится. В этом интервале с помощью интеграла Эйлера гамма-функция не может быть определена. При  = 1 имеем:

.

Приняв в интеграле Эйлера x = t², получим

.

Приравняв  = 1/2 , имеем

.

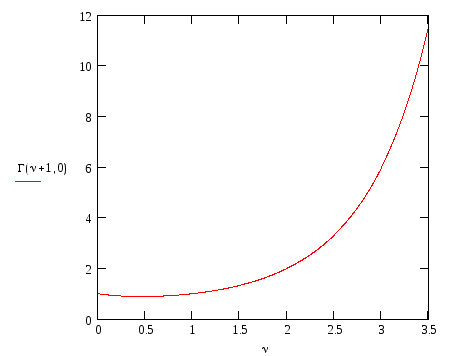
Рис. 6.3. График гамма-функции

Применим к интегралу Эйлера формулу интегрирования по частям: , полагая;;;.

.

Это основная формула приведения для Г-функции. Из нее следует, что

.

Применив эту формулу последовательно kраз, получим:

, ( – k > 0).

В математических справочниках значения гамма-функции обычно даются лишь для величин v, лежащих в диапазоне 1 <  < 2. чтобы найти значение Г-функции в другом диапазоне, нужно использовать приведенную формулу. Для нахождения Г() при  > 2 мы должны выбирать целое k > 0 таким образом, чтобы выполнялось условия: 1   – k < 2.

Если  = n, где n > 0 – целое число, то

Г (n)=(n – 1)!

Применив формулу приведения для  = n + 1/2 и учитывая, что , получим

,

где (2n – 1)!! = .

До сих пор мы считали, что аргумент  функции Г() больше нуля. Доопределим теперь функцию гамма для отрицательных значений аргумента. Учитывая формулу приведения, запишем:

.

Положим =^*, тогда

.

Обозначив в последней формуле ^* снова через , получим

.

Если  + k > 0 и … (k = 1, 2, 3,...), то правая часть формулы имеет смысл и при  < 0. Последнюю формулу принимают за определение гамма-функции при отрицательных значениях аргумента . Очевидно, она не существуют при целых отрицательных значениях  (при таких значениях  она обращается в бесконечность).

Теперь мы можем обобщить биномиальную теорему на случай действительных (и даже комплексных чисел).

Теорема 6.2. Пусть – произвольное комплексное число. Тогда для любого комплексного числа , удовлетворяющего условию , справедливо

, (6.3)

где .

Пример 6.1. Приведем примеры некоторых биномиальных разложений, полученных с помощью формулы (6.3):