Лекция № 8. Числа фибоначчи и простые числа

1. Задача Фибоначчи

Итальянский математик Леонардо Фибоначчи жил в 13 столетии и одним из первых в Европе стал использовать арабские (индийские) цифры. Он придумал несколько искусственную задачу о кроликах, которых выращивают на ферме, причем все они считаются самками, самцы игнорируются. Кролики начинают размножаться после того, как им исполняется два месяца, а потом каждый месяц рожают по кролику. Кролики никогда не умирают.

Нужно определить, сколько кроликов будет на ферме через n месяцев, если в начальный момент времени был только один новорожденный кролик.

Очевидно, что фермер имеет одного кролика в первый месяц и одного кролика – во второй месяц. На третий месяц будет уже два кролика, на четвертый – три и т.д. Обозначим количество кроликов в n месяце как . Таким образом,,,,,, …

Можно построить алгоритм, позволяющий найти при любомn.

Согласно условию задачи общее количество кроликов вn+1 месяце раскладывается на три составляющие:

• одномесячные кролики, не способные к размножению, в количестве

;

• кролики, способные к размножению, в количестве ;

• новорожденные кролики, их количество также равно .

Таким образом, получим

. (8.1)

Формула (8.1) позволяет вычислить ряд чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, …

Числа в данной последовательности называются числами Фибоначчи.

Если принять и , то с помощью формулы (8.1) можно определить все остальные числа Фибоначчи. Формула (8.1) называется рекуррентной формулой (recurrence – «возвращение» на латыни).

Пример 8.1. Предположим, что имеется лестница в n ступенек. Мы можем подниматься по ней с шагом в одну ступеньку, либо – с шагом в две ступеньки. Сколько существует комбинаций различных способов подъема?

Если n = 1, имеется только один вариант решения задачи. Для n = 2 существует 2 варианта: два единичных шага либо один двойной. Для n = 3 существует 3 варианта: три единичных шага, либо один единичный и один двойной, либо один двойной и один единичный.

В следующем случае n = 4, имеем 5 возможностей (1+1+1+1, 2+1+1, 1+2+1, 1+1+2, 2+2).

Для того чтобы ответить на заданный вопрос при произвольном n, обозначим количество вариантов как , и попробуем определитьпо известными . Если мы стартуем с единичного шага, то имеем комбинаций для оставшихсяn ступенек. Если стартуем с двойного шага, то имеем комбинаций для оставшихсяn–1 ступенек. Общее количество вариантов для n+1 ступенек равно

. (8.2)

Полученная формула как близнец напоминает формулу (8.1). Тем не менее, это не позволяет отождествлять количество комбинаций с числами Фибоначчи. Мы видим, например, что, но. Однако имеет место следующая зависимость:

.

Это справедливо для n = 1, 2, и также справедливо для каждого n. Числа Фибоначчи и количество комбинаций вычисляются по одной и той же формуле, однако начальные значения,и,у них различаются.

Пример 8.2. Этот пример имеет практическое значение для задач помехоустойчивого кодирования. Найдем число всех двоичных слов длины n, не содержащих несколько нулей подряд. Обозначим это число через . Очевидно,, а слова длины 2, удовлетворяющие нашему ограничению, таковы: 10, 01, 11, т.е.. Пусть– такое слово изn символов. Если символ , томожет быть произвольным ()-буквенным словом, не содержащим несколько нулей подряд. Значит, число слов с единицей на конце равно.

Если же символ , то обязательно, а первыесимволамогут быть произвольными с учетом рассматриваемых ограничений. Следовательно, имеетсяслов длины n с нулем на конце. Таким образом, общее число интересующих нас слов равно

.

С учетом того, что и, полученная последовательность чисел – это числа Фибоначчи.

Пример 8.3. В примере 7.6 мы нашли, что число двоичных слов постоянного веса t (и длиной k) равно . Теперь найдем число двоичных слов постоянного весаt, не содержащих несколько нулей подряд.

Рассуждать можно так. Пусть число нулей в рассматриваемых словах. В любом слове имеетсяпромежутков между ближайшими нулями, в каждом из которых находится одна или несколько единиц. Предполагается, что. В противном случае нет ни одного слова без рядом стоящих нулей.

Если из каждого промежутка удалить ровно по одной единице, то получим слово длины , содержащеенулей. Любое такое слово может быть получено указанным образом из некоторого (и притом только одного)k-буквенного слова, содержащего нулей, никакие два из которых не стоят рядом. Значит, искомое число совпадает с числом всех слов длины, содержащих ровнонулей, т.е. равно.

Пример 8.4. Докажем, что сумма равна числам Фибоначчи для любого целого. Символобозначаетнаименьшее целое число, большее или равное . Например, если, то; а если, то. По-английски эту операцию называютceil («потолок»). Также встречается символ , который обозначаетнаибольшее целое число, меньшее или равное . По-английски эту операцию называютfloor («пол»).

Если , то. Если, то. Если, то.

Таким образом, для рассмотренных случаев сумма действительно равна числам Фибоначчи. Теперь приведем доказательство для общего случая. Поскольку числа Фибоначчи можно получить с помощью рекуррентного уравнения (8.1), то должно выполняться равенство:

.

И оно действительно выполняется:

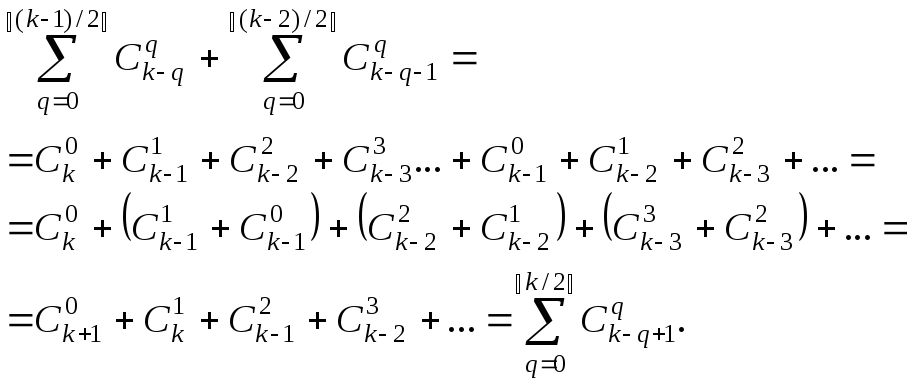
Здесь мы использовали полученную ранее формулу (4.4): .

2. Сумма чисел Фибоначчи

Определим сумму первых n чисел Фибоначчи.

0 = 0,

0+1 = 1,

0+1+1 = 2,

0+1+1+2 = 4,

0+1+1+2+3 = 7,

0+1+1+2+3+5 = 12,

0+1+1+2+3+5+8 = 20,

0+1+1+2+3+5+8+13 = 33.

Легко заметить, что прибавлением к правой части каждого уравнения единицы мы снова получаем число Фибоначчи. Общая формула для определения суммы первых n чисел Фибоначчи имеет вид:

.

Докажем это, используя метод математической индукции. Для этого запишем:

.

Эта сумма должна быть равна .

.

Сократив левую и правую часть уравнения на –1, получим уравнение (6.1).

3. Формула для чисел Фибоначчи

Теорема 8.1. Числа Фибоначчи можно рассчитать по формуле

.

Доказательство. Убедимся в справедливости этой формулы для n = 0, 1, а затем докажем справедливость данной формулы для произвольного n по индукции. Вычислим отношение двух ближайших чисел Фибоначчи:

Мы видим, что отношение этих чисел колеблется около значения 1.618 (если игнорировать несколько первых значений). Этим свойством числа Фибоначчи напоминают члены геометрической прогрессии. Примем , (). Тогда выражение

преобразуется в

,

которое после упрощений выглядит так

.

Мы получили квадратное уравнение, корни которого равны:

Теперь можем записать:

(где c является константой). Оба члена и не дают чисел Фибоначчи, например , в то время как. Однако разность удовлетворяет рекуррентному уравнению:

.

Для n=0 эта разность дает, то есть: . Однако при n=1 мы имеем . Чтобы получить , необходимо принять:.

Теперь мы имеем две последовательности: и , которые начинаются с одинаковых двух чисел и удовлетворяют одной и той же рекуррентной формуле. Они должны быть равны: . Теорема доказана.

При возрастании n член становится очень большим, в то время как, и роль членав разности сокращается. Поэтому при больших n приближенно можем записать

.

Мы игнорируем 1/2 (поскольку числа Фибоначчи возрастают до бесконечности при росте n до бесконечности).

Отношение называется золотым сечением, его используют за пределами математики (например, в скульптуре и архитектуре). Золотым сечением является отношение между диагональю и стороной правильного пятиугольника (рис. 8.1).

Рис. 8.1. Правильный пятиугольник и его диагонали

Для обозначения золотого сечения принято использовать букву в честь известного афинского скульптора Фидия.

4. Простые числа

Все натуральные числа, большие единицы, распадаются на два класса. К первому относятся числа, имеющие ровно два натуральных делителя, единицу и самого себя, ко второму – все остальные. Числа первого класса называют простыми, а второго – составными. Простые числа в пределах первых трех десятков: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, …

Свойства простых чисел и их связь со всеми натуральными числами изучалась Евклидом (3 век до нашей эры). Если выписывать простые числа подряд, то можно заметить, что относительная плотность их убывает. На первый десяток их приходится 4, т. е. 40%, на сотню – 25, т.е. 25%, на тысячу – 168, т.е. меньше 17%, на миллион – 78498, т.е. меньше 8%, и т.д.. Тем не менее, их общее число бесконечно.

Среди простых чисел попадаются пары таких, разность между которыми равна двум (так называемые простые близнецы), однако конечность или бесконечность таких пар не доказана.

Евклид считал очевидным, что с помощью умножения только простых чисел можно получить все натуральные числа, причем каждое натуральное число представимо в виде произведения простых чисел единственным образом (с точностью до порядка множителей). Таким образом, простые числа образуют мультипликативный базис натурального ряда.

Изучение распределения простых чисел привело к созданию алгоритма, позволяющего получать таблицы простых чисел. Таким алгоритмом является решето Эратосфена (3 век до нашей эры). Этот метод заключается в отсеивании (например, путем зачеркивания) тех целых чисел заданной последовательности , которые делятся хотя бы на одно из простых чисел, меньших.

Теорема 8.2. (теорема Евклида). Число простых чисел бесконечно.

Доказательство. Теорему Евклида о бесконечности числа простых чисел докажем способом, предложенным Леонардом Эйлером (1707–1783). Эйлер рассмотрел произведение по всем простым числам p:

при . Это произведение сходится, и если его раскрыть, то в силу однозначности разложения натуральных чисел на простые сомножители получается, что оно равняется сумме ряда, откуда следует тождество Эйлера:

.

Так как при ряд справа расходится (гармонический ряд), то из тождества Эйлера следует теорема Евклида.

Русский математик П.Л. Чебышев (1821–1894) вывел формулу, определяющую пределы, в которых заключено число простых чисел , не превосходящихX:

,

где ,.