Лекция № 9. Кодирование

1. Введение

Вопросы кодирования издавна играли заметную роль в математике. Десятичная позиционная система счисления – это способ кодирования натуральных чисел. Римские цифры – другой способ кодирования натуральных чисел, причем гораздо более наглядный и естественный: палец – I, пятерня – V, две пятерни – X. Однако при этом способе кодирования труднее выполнять арифметические операции над большими числами, поэтому он был вытеснен позиционной десятичной системой. Любопытно, что у римлян не было символа для обозначения нуля.

Декартовы координаты – способ кодирования геометрических объектов числами.

Задачу кодирования можно сформулировать следующим образом, Пусть заданы алфавиты ,и функция, где– некоторое множество слов в алфавите,. Тогда функцияназываетсякодированием, элементы множества –сообщениями, а элементы –кодами соответствующих сообщений.

Обратная функция (если она существует) называетсядекодированием.

Если , тоназываетсяn-ичным кодированием. Наиболее распространенный случай –двоичное кодирование. Именно этот случай рассматривается далее.

2. Алфавитное кодирование

Кодирование может сопоставлять код всему сообщению из множествакак единому целому или же строить код сообщения из кодов его частей. Если элементарной частью сообщения является одна буква алфавита, то такое кодирование называетсяалфавитным.

Пусть задано конечное множество , которое называетсяалфавитом. Элементы алфавита называются буквами. Последовательность букв называется словом. Множество слов в алфавите A обозначается . Если слово, то количество букв в слове называетсядлиной слова: .

Пустое слово обозначается .

Если , тоназывается началом, илипрефиксом, слова , а– окончанием, илипостфиксом, слова . Если при этом(соответственно,), то(соответственно,) называетсясобственным началом (соответственно, собственным окончанием) слова .

Алфавитное (или побуквенное) кодирование задается схемой (или таблицей кодов) :

.

Множество кодов букв называется множествомэлементарных кодов. Алфавитное кодирование пригодно для любого множества сообщений :

, ,.

Пример 9.1. Рассмотрим алфавиты ,и схему:

Эта схема однозначна, но кодирование не является взаимно однозначным: , а значит, невозможно декодирование. С другой стороны, схема

известная под названием «двоично-десятичное кодирование», допускает однозначное декодирование.

3. Разделимые схемы

Рассмотрим схему алфавитного кодирования и различные слова, составленные из элементарных кодов. Схеманазываетсяразделимой, если

,

то есть любое слово, составленное из элементарных кодов, единственным образом разлагается на элементарные коды. Алфавитное кодирование с разделимой схемой допускает декодирование.

Схема называетсяпрефиксной, если элементарный код одной буквы не является префиксом элементарного кода другой буквы:

.

Теорема 9.1. Префиксная схема является разделимой.

Доказательство. От противного. Пусть кодирование со схемой не является разделимым. Тогда существует такое слово, что

.

Поскольку , значит,, но это противоречит тому, что схема префиксная.

Замечание. Свойство быть префиксной является достаточным, но не является необходимым для разделимости схемы.

Пример 9.2. Разделимая, но не префиксная схема: ,,.

Чтобы схема алфавитного кодирования была разделимой, необходимо, чтобы длины элементарных кодов удовлетворяли определенному соотношению, известному как неравенство Макмиллана.

Теорема 9.2. Если схема разделима, то

, где .

Доказательство. Обозначим: . Рассмотримn-ю степень левой части неравенства . Раскрывая скобки, имеем сумму, где– различные наборы номеров элементарных кодов. Обозначим черезколичество входящих в эту сумму слагаемых вида, где. Для некоторыхможет быть=0. Приводя подобные, имеем сумму. Каждому слагаемому видаможно однозначно сопоставить код (слово в алфавитеB) вида . Это слово состоит изn элементарных кодов и имеет длину t.

Таким, образом, – это число некоторых слов вида, таких что. В силу разделимости схемы, в противном случае заведомо существовали бы два одинаковых слова, допускающих различное разложение. Имеем

.

Следовательно, , и значит,, откуда

.

Неравенство Макмиллана является не только необходимым, но и достаточным условием разделимости схемы алфавитного кодирования.

Пример 9.3. Азбука Морзе – это схема алфавитного кодирования

,

где по историческим и техническим причинам 0 называется точкой, а 1 называется тире. Имеем

1/4+1/16+1/16+1/8+1/2+1/16+1/8+1/16+1/4+1/16+1/8+1/16+1/4+1/4+

+1/8+1/16+1/16+1/8+1/8+1/2+1/8+1/16+1/8+1/16+1/16+1\16=

=2/2+4/4+7/8+12/16=3+5/8 > 1.

Таким образом, неравенство Макмиллана для азбуки Морзе не выполнено, и эта схема не является разделимой. На самом деле в азбуке Морзе имеются дополнительные элементы – паузы между буквами (и словами), которые позволяют декодировать сообщения. Эти дополнительные элементы определены неформально, поэтому прием и передача сообщений с помощью азбуки Морзе, особенно с высокой скоростью, является некоторым искусством, а не простой технической процедурой.

4. Помехоустойчивое кодирование

Пусть имеется канал связи C, содержащий источник помех:

,

где S – множество переданных, а – соответствующее множество принятых по каналу сообщений. КодированиеF, обладающее таким свойством, что

,

называется помехоустойчивым.

Если A=B={0,1}, то ошибки в канале могут быть следующих типов:

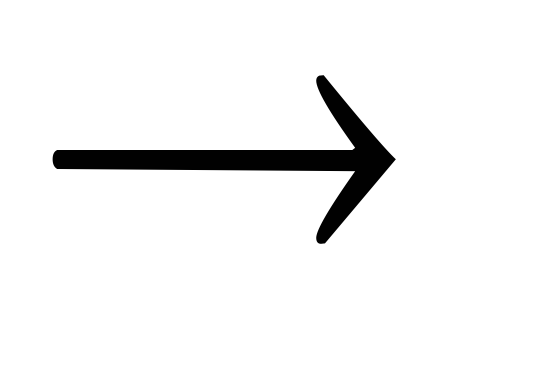• 01, 10 – ошибка типа замещения разряда;

• 0, 1– ошибка типа выпадения разряда;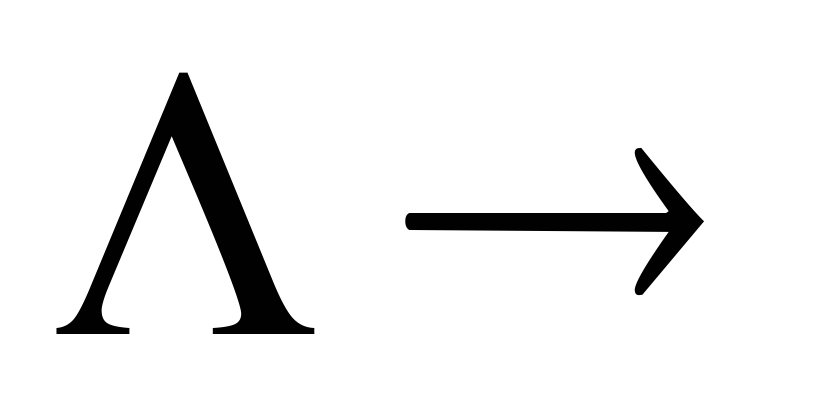

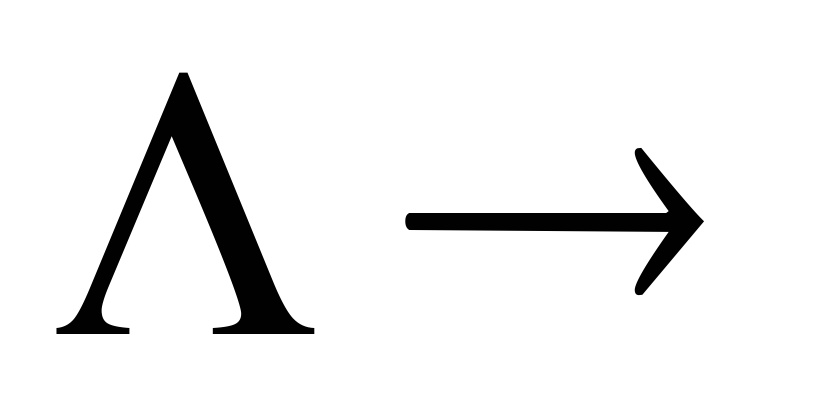• 1, 0 – ошибка типа вставки разряда.

Пусть – множество слов, которые могут быть получены из словаs в результате всех возможных комбинаций допустимых в канале ошибок , то есть,. Если, то та конкретная последовательность ошибок, которая позволяет получить из словаs слово , обозначается. Если тип возможных ошибок в канале подразумевается, то индексне указывается.

Теорема 9.3. Чтобы существовало помехоустойчивое кодирование с исправлением всех ошибок, необходимо и достаточно, чтобы , то есть необходимо и достаточно, чтобы существовало разбиение множества B* на множества , такое что.

Доказательство. Если кодирование помехоустойчивое, то очевидно, что . Обратно: по разбиениюстроится функция.

Рассмотрим множество из всехдвоичных последовательностей (векторов), имеющих вид

.

Введем в множестве операцию сложения +, определив для последовательностейиих сумму с помощью соотношения:, где– это сумма по модулю два.

Расстояние Хэмминга между кодовыми словами определяется как число позицийтаких, что. При построении векторапары одинаковых двоичных символовбудут давать 0 , а пары различных двоичных символов будут давать 1.

Пример 9.4. (0, 1, 0, 1)+(1, 1, 1, 0)=(1, 0, 1, 1).

Поэтому расстояние Хэмминга можно определить как число компонент вектора, которые равны 1.

Введенное таким образом расстояние Хэмминга удовлетворяет следующим условиям:

• 

• ;

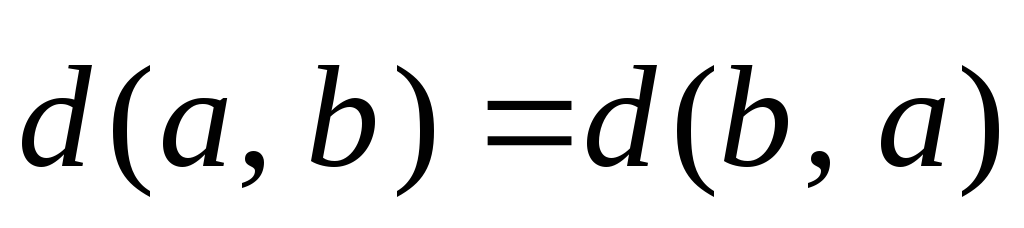• –«неравенство треугольника».

В общем случае расстоянием называют функцию, удовлетворяющую вышеприведенным условиям. Этим условиям, в частности, удовлетворяет геометрическое расстояние между двумя точками () и () на плоскости:.

При наличии бит можно построитькодовых слов. Однако часто нужны не все из этих слов. Если использовать только часть кодовых слов, то с помощью проверок на четность и других приемов можно обнаружить ошибки и даже их исправлять.

Предположим, что из используются толькослов:. Если эти слова таковы, что при всех:

, (7.1)

то можно исправлять любые ошибки кратности .

Допустим, что в некоторых компонентах слова при передаче возникли ошибки, в результате которых символы 0 были приняты как 1, а символы 1 – как 0 (ошибки типа замещения). Получившееся в результате словонаходится на расстоянииот слова. Следовательно, если считать, что ошибки при передаче могут возникать не более чем вкомпонентах, то совокупность всех слов, которые могут получиться из, представляет собой множество.

Из неравенства треугольника и условия (7.1) следует , если только. Действительно, допустим, что существует слово. Тогдаи.

Согласно неравенству треугольника

,

что приводит к противоречию с условием (9.1).

Множество называетсяобластью декодирования для слова . Так как области декодирования не пересекаются, то при приеме слова из области декодированияможно считать, что передавалось слово. Если при этом число ошибок не превосходит, то при приеме всегда будет приниматься правильное решение.

Так как число элементов в множестверавно числу способов выбора некоторых() компонент слова, то

.

Далее, так как , то:, то есть

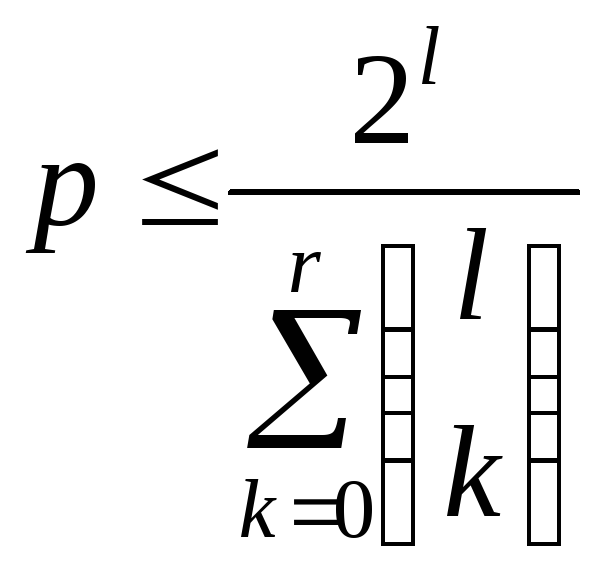. (9.2)

Неравенство (9.2) называется границей Хэмминга. Оно дает оценку сверху для числа кодовых слов, которые можно использовать для передачи, если их длина равнабит и нужно исправлять все-кратные ошибки.

Пример 9.5. Пусть =8, тогда. Поскольку, то;;;;.

Если =4, то.

Если =3, то.

Если =2, то.

Если =1, то.

Если =0, то.

Таким образом, если встречаются только одиночные ошибки типа замещения, то при использовании 8 бит можно безошибочно передавать 28 слов. В общем случае, если имеется бит и нужно исправлять одиночные ошибки типа замещения, то граница Хэмминга определяется следующим выражением, являющимся частным случаем формулы (9.2):

. (9.3)

Обозначим минимальное число бит, необходимое для передачи слов, буквой. Тогда:, и из формулы (9.3) следует

. (9.4)

Таким образом, для помехоустойчивого кодирования сигналов при одиночных ошибках типа замещения необходимо использовать дополнительные бит, количество которых должно удовлетворять условию (9.4). Рассматриваемый случай простейший, но одновременно практически очень важный. Таким свойством, как правило, обладают внутренние шины передачи данных в современных компьютерах.

Пример 9.6. Для сообщения длиной потребуетсядополнительных разрядов, поскольку 64=.

Код, в котором используются дополнительные разряды для помехоустойчивой передачи сигналов, называется кодом Хэмминга.